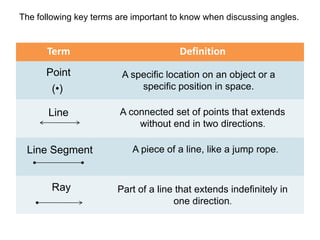
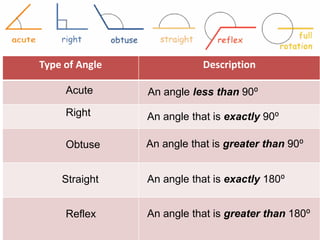
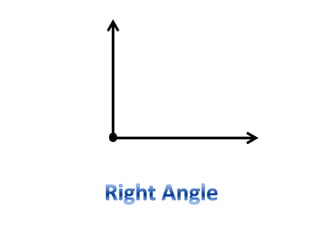
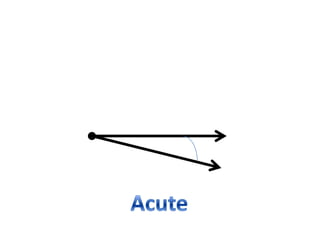
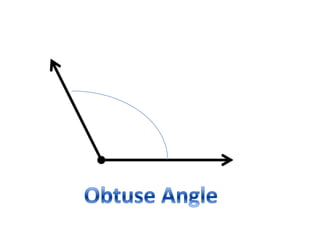
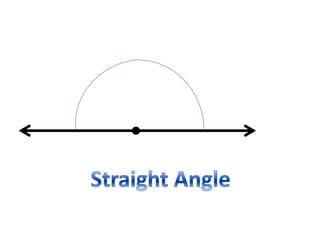
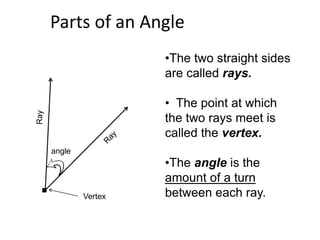
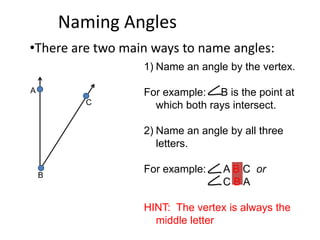
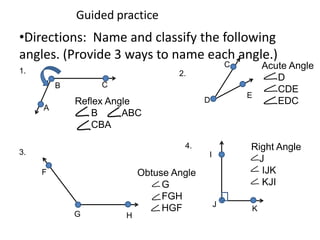
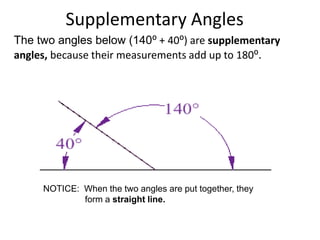
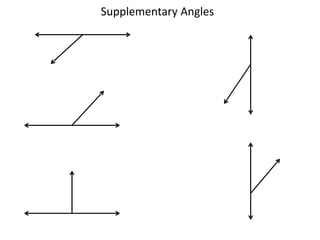
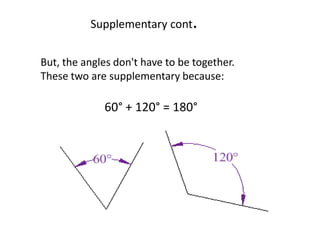
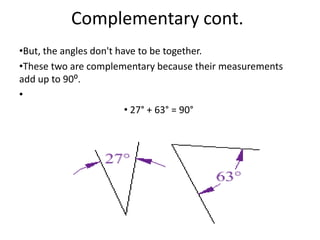
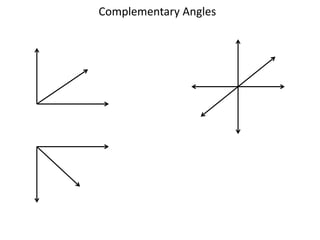
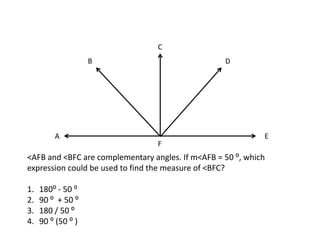
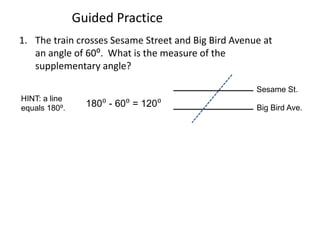
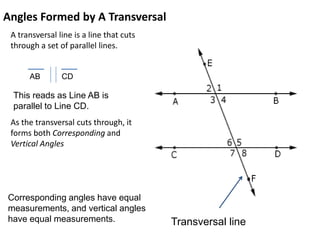
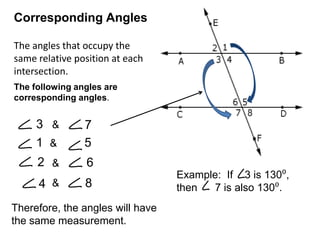
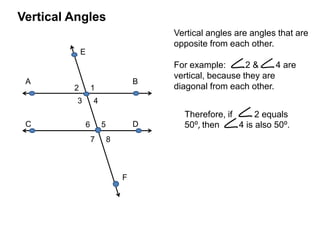
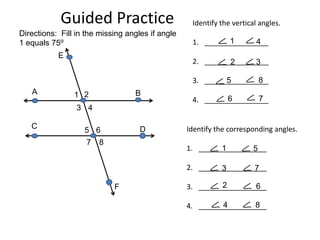
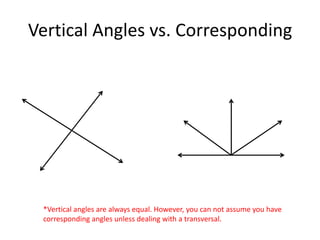
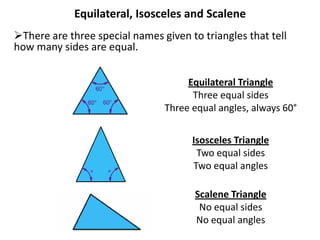
* There are 3 angles in a triangle * The sum of the angles is 180° * We are given: Angle 1 = 85°, Angle 2 = 60° * So: Angle 1 + Angle 2 + Angle 3 = 180° * 85° + 60° + Angle 3 = 180° * 145° + Angle 3 = 180° * Angle 3 = 180° - 145° = 35° Therefore, the missing angle is 35°.

1. Geometry
Lesson 3
Tennessee
Adult Education
This curriculum was written with funding of the Tennessee Department of Labor and Workforce Development and may not be reproduced in any way without written permission. ©

2. What is Geometry?
•It is the branch of mathematics that deals with
lines, points, curves, angles, surfaces, and solids.

3. The following key terms are important to know when discussing angles.
Term Definition
Point A specific location on an object or a
(•) specific position in space.
Line A connected set of points that extends
without end in two directions.
Line Segment A piece of a line, like a jump rope.
Ray Part of a line that extends indefinitely in
one direction.

4. Term Definition
Parallel Lines Lines that are always the same distance They
will never intersect.
Perpendicular
Lines that form a right angle when they
Lines
intersect
Intersecting Lines Lines that cross, or that will cross. The point at
which they cross is called the vertex.
Transversal Lines Lines that intersect a set of parallel lines.

5. What are angles?
•An angle measures the amount of a turn.
•As the Angle Increases, the Name Changes.
Mr. Smiles fell
at an angle of
90⁰. He fell at
a right angle.
Pictures from clipart

6. Type of Angle Description
Acute An angle less than 90⁰
Right An angle that is exactly 90⁰
Obtuse An angle that is greater than 90⁰
Straight An angle that is exactly 180⁰
Reflex An angle that is greater than 180⁰

7. Find the Angles!

12. Walnut St. Bridge, Chattanooga

14. Review!

20. Parts of an Angle
•The two straight sides
are called rays.
• The point at which
Ray
the two rays meet is
called the vertex.
angle
•The angle is the
amount of a turn
· Vertex between each ray.

21. Naming Angles
•There are two main ways to name angles:
1) Name an angle by the vertex.
A For example: B is the point at
C which both rays intersect.
2) Name an angle by all three
letters.
B
For example: A B C or
CBA
HINT: The vertex is always the
middle letter

22. Guided practice
•Directions: Name and classify the following
angles. (Provide 3 ways to name each angle.)
C Acute Angle
1. 2.
D
B C
CDE
E
Reflex Angle D EDC
A
B ABC
CBA
4. Right Angle
3. I
J
F Obtuse Angle IJK
G KJI
FGH
J
HGF K
G H

23. Supplementary Angles
The two angles below (140⁰ + 40⁰) are supplementary
angles, because their measurements add up to 180⁰.
NOTICE: When the two angles are put together, they
form a straight line.

24. Supplementary Angles

25. Supplementary cont.
But, the angles don't have to be together.
These two are supplementary because:
60° + 120° = 180°

26. Complementary Angles
•The two angles at the right
(40° + 50°) are
Complementary Angles,
because they add up to 90°.
•NOTICE: When the
two angles are placed
together, they form a
corner.

27. Complementary cont.
•But, the angles don't have to be together.
•These two are complementary because their measurements
add up to 90⁰.
•
• 27° + 63° = 90°

28. Complementary Angles

29. Complementary vs Supplementary
How can you remember which is which? Easy! Think:
• "C" of Complementary stands for "Corner" (a Right
Angle), and
• "S" of Supplementary stands for "Straight" (180
degrees is a straight line)

30. Find the missing angle using complementary or supplementary angles.
80

31. Find the missing angle using complementary or supplementary angles.
155

32. Find the missing angle using complementary or supplementary angles.
30

33. Find the missing angle using complementary or supplementary angles.
47

34. C
B D
A E
F
<AFB and <BFC are complementary angles. If m<AFB = 50 ⁰, which
expression could be used to find the measure of <BFC?
1. 180⁰ - 50 ⁰
2. 90 ⁰ + 50 ⁰
3. 180 / 50 ⁰
4. 90 ⁰ (50 ⁰ )

35. Guided Practice
1. The train crosses Sesame Street and Big Bird Avenue at
an angle of 60⁰. What is the measure of the
supplementary angle?
Sesame St.
HINT: a line
equals 180⁰. 180⁰ - 60⁰ = 120⁰ Big Bird Ave.

36. 2. Jo Jo is building a fence. In order to make it stronger,
she will need to use a brace from one side to the ground.
If the brace makes a 45⁰ angle with the fence what is the
measure of the supplementary angle?

38. Angles Formed by A Transversal
A transversal line is a line that cuts
through a set of parallel lines.
AB CD
This reads as Line AB is
parallel to Line CD.
As the transversal cuts through, it
forms both Corresponding and
Vertical Angles
Corresponding angles have equal
measurements, and vertical angles
have equal measurements. Transversal line

39. Corresponding Angles
The angles that occupy the
same relative position at each
intersection.
The following angles are
corresponding angles.
3 & 7
1 & 5
2 & 6
Example: If 3 is 130⁰,
4 & 8 then 7 is also 130⁰.
Therefore, the angles will have
the same measurement.

40. Vertical Angles
Vertical angles are angles that are
opposite from each other.
E
For example: 2& 4 are
vertical, because they are
A B
2 1 diagonal from each other.
3 4
Therefore, if 2 equals
C 6 5 D 50⁰, then 4 is also 50⁰.
7 8
F

41. Guided Practice Identify the vertical angles.
Directions: Fill in the missing angles if angle
1 equals 75⁰ 1 4
1. ________________
E
2. ________________
2 3
8
3. ________________
5
A 1 2 B
6 7
4. ________________
3 4
C D Identify the corresponding angles.
5 6
7 8
1. _________________
1 5
2. _________________
3 7
F 2 6
3. _________________
4 8
4. _________________

42. 1 2 3 4
5 6 7 8
If the lines are parallel and m<2 is 45⁰ in the figure above, what is
the measure of <3?
1. 30 ⁰
2. 45 ⁰
3. 90 ⁰
4. 135 ⁰
5. 180 ⁰

43. Vertical Angles vs. Corresponding
*Vertical angles are always equal. However, you can not assume you have
corresponding angles unless dealing with a transversal.

44. Triangles
Why do I need to know about triangles?
The GED Test will ask testers to identify missing angles. In order to
answer those questions, a person must have an understanding of
triangles and their characteristics.
A triangle has three sides and three angles
The three angles always add up to 180°
a
a + b + c = 180⁰
b c

45. Equilateral, Isosceles and Scalene
There are three special names given to triangles that tell
how many sides are equal.
Equilateral Triangle
Three equal sides
Three equal angles, always 60°
Isosceles Triangle
Two equal sides
Two equal angles
Scalene Triangle
No equal sides
No equal angles

46. Find the missing angle measurement.
70
55

47. Find the missing angle measurement.
50 50

48. Find the missing angle measurement.
85 60