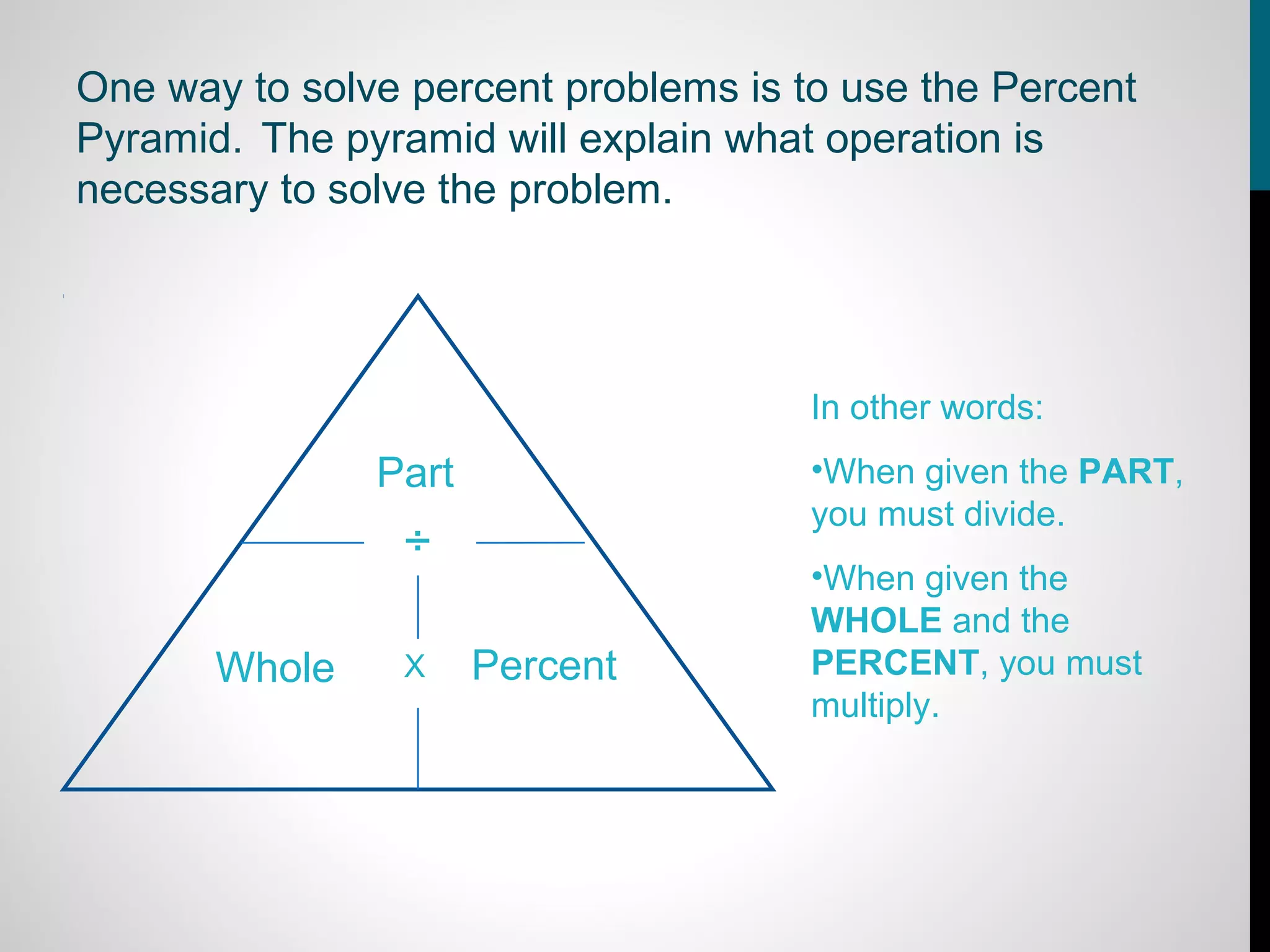
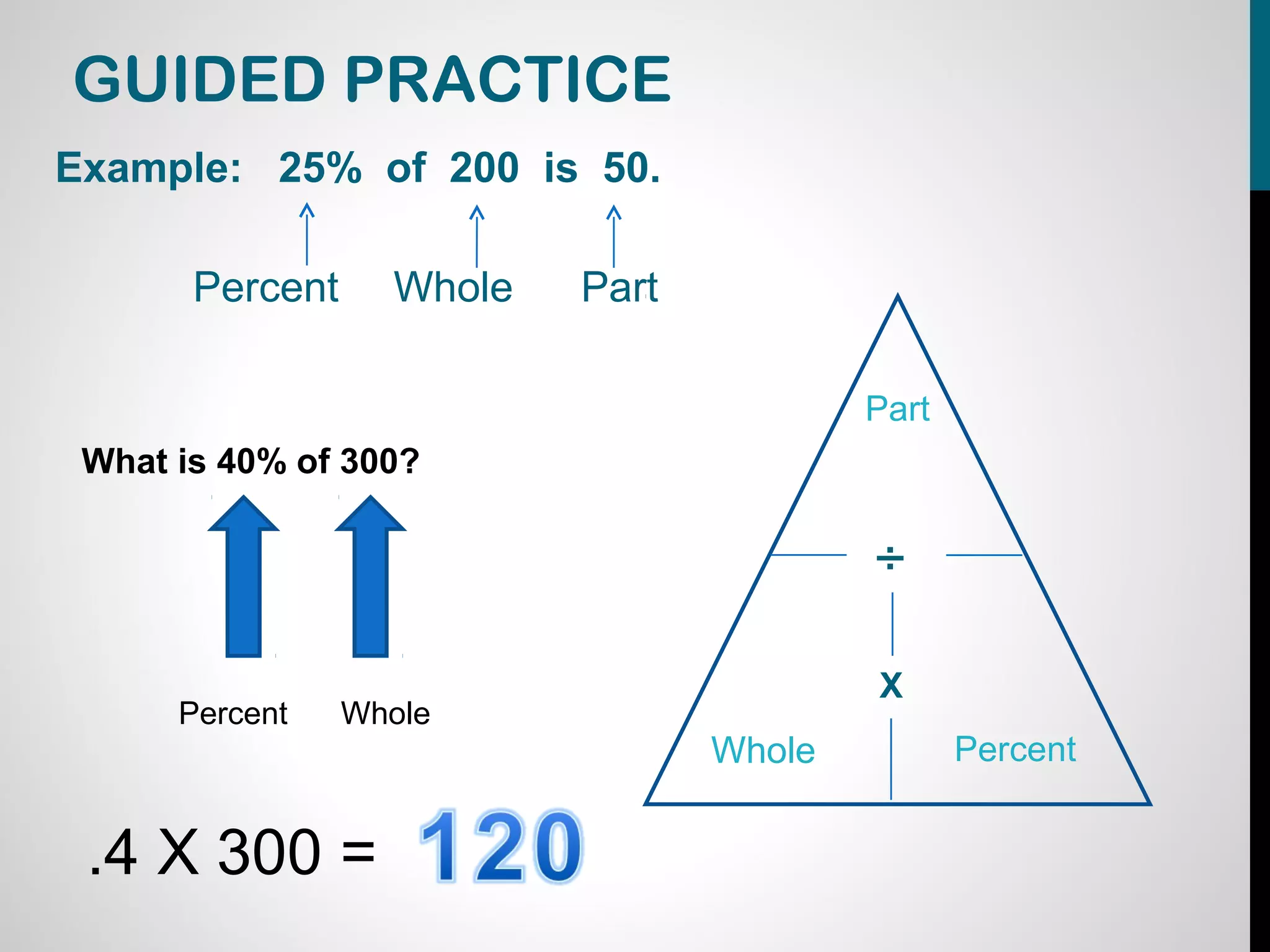
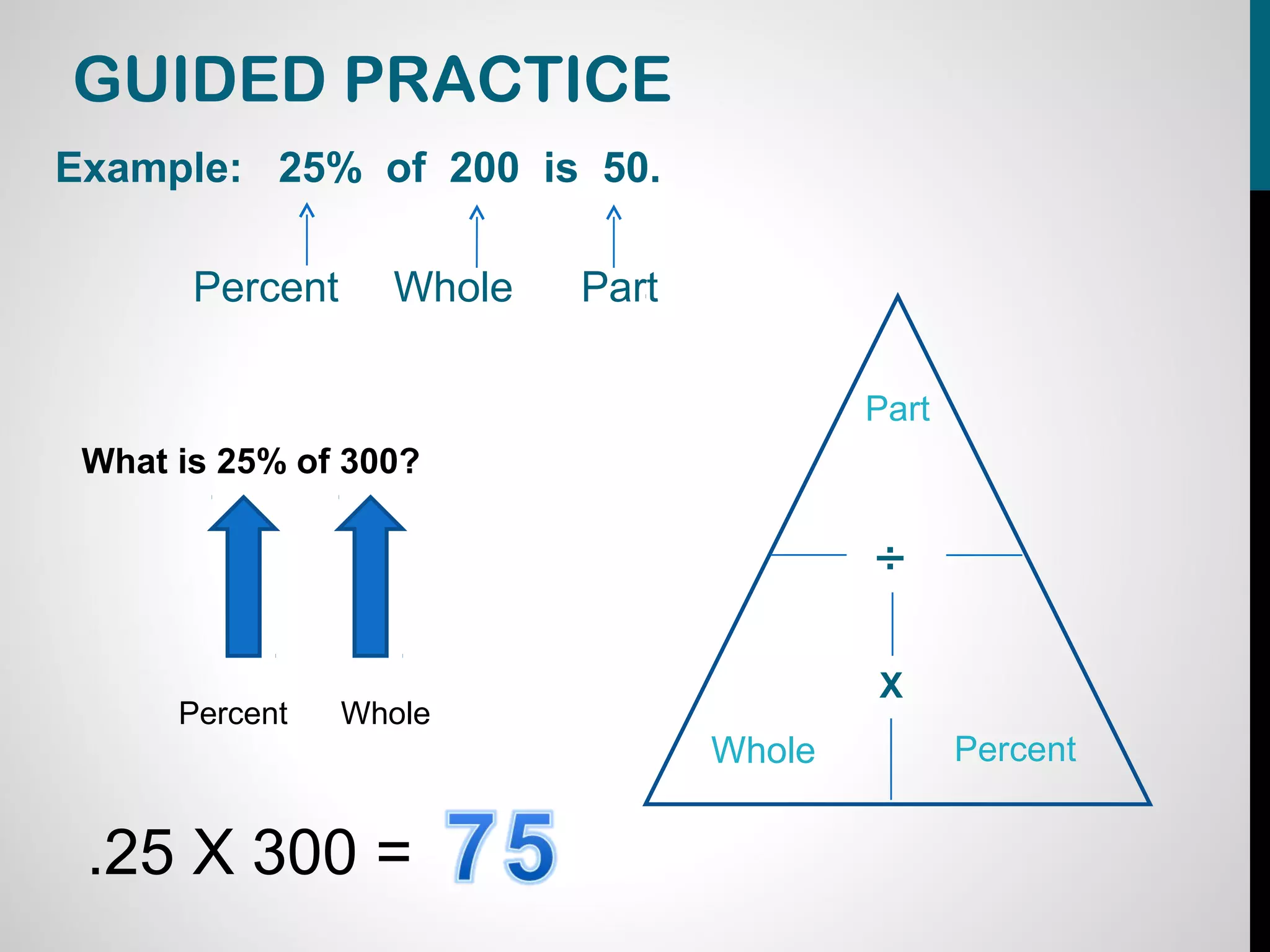
The document provides information about calculating percentages. It defines percent as parts out of 100 and explains that percent problems involve solving for the percent, whole, or part. It demonstrates how to change percents to decimals and decimals to percents by moving the decimal point. The document uses examples and guided practice problems to illustrate how to set up and solve percent problems using a percent pyramid diagram. It emphasizes understanding what each number represents and whether to multiply or divide to solve the problem.

1. PERCENTS
LESSON 2
TENNESSEE
ADULT EDUCATION
This curriculum was written with funding of the Tennessee Department of Labor and Workforce Development and may not be reproduced in any way without written permission. ©

2. WHAT IS PERCENT?
It’s the number of parts out of 100.
25% means 25 parts out of 100

3. WHEN SOLVING PERCENT PROBLEMS, YOU WILL BE
SOLVING FOR ONE OF THESE THREE PARTS.
E
Percent Whole Part

4. 25% OF THE PIZZA
Does 25% = 25?
No.
There are not 25 pizzas.
25% is 25 slices out of 100 total.

5. BEFORE SOLVING PERCENT PROBLEMS, IT IS
NECESSARY TO CHANGE THE PERCENT TO A
DECIMAL.
 When given the percent, always move the decimal 2
places to the left.
For example: 13% = .13
Tenths
Ones
Hundredths
Tens Thousandths
Hundreds
000 130 .
decimal
Let’s practice changing the following percents to decimals.
1. 62% = _____ 2. 122% = _____ 3. 2% = _____

6. AT THE END OF PROBLEMS, YOU MAY NEED TO
CHANGE FROM A DECIMAL BACK INTO A PERCENT.
 When you have a decimal, always move the decimal 2
places to the right to make a percent.
For example: .6 = 60%
Tenths
Ones
Hundredths
Tens Thousandths
Hundreds
000 600 .
decimal
Let’s practice changing the following percents to decimals.
1. .33 = _____ 2. .6 = _____ 3. .03 = _____

7. WHEN SOLVING PERCENT PROBLEMS, YOU WILL BE
SOLVING FOR ONE OF THESE THREE PARTS.
Example: 25% of 200 is 50.
Percent Whole Part

8. One way to solve percent problems is to use the Percent
Pyramid. The pyramid will explain what operation is
necessary to solve the problem.
In other words:
Part •When given the PART,
you must divide.
÷
•When given the
WHOLE and the
Whole X Percent PERCENT, you must
multiply.

9. The following charts provide key words that will
help identify what each number represents in a
word problem.
Whole Part
F Follows the word “is”
Discounted Price
Interest
Down Payment
Amount Paid
Taxes
Tips

10. GUIDED PRACTICE
Example: 25% of 200 is 50.
Percent Whole Part
Part
What is 20% of 30?
÷
X
Percent Whole
Whole Percent
.2 X 30 =

11. GUIDED PRACTICE
Example: 25% of 200 is 50.
Percent Whole Part
Part
What is 40% of 300?
÷
X
Percent Whole
Whole Percent
.4 X 300 =

12. GUIDED PRACTICE
Example: 25% of 200 is 50.
Percent Whole Part
Part
What is 25% of 300?
÷
X
Percent Whole
Whole Percent
.25 X 300 =

13. GUIDED PRACTICE
Example: 25% of 200 is 50.
Percent Whole Part
Part
What % of 300 is 30?
÷
X
Whole Part
Whole Percent
30 ÷ 300 =

14. GUIDED PRACTICE
Example: 25% of 200 is 50.
Percent Whole Part
Part
What % of 100 is 50?
÷
X
Whole Part
Whole Percent
50 ÷ 100 =

15. GUIDED PRACTICE
Example: 25% of 200 is 50.
Percent Whole Part
Part
20 is what percent of 100.
÷
X
Part Whole
Whole Percent
20 ÷ 100 =

16. GUIDED PRACTICE
Directions: Solve each problem using the Percent Pyramid.
Draw out the pyramid for each problem.
1.30% of 90 = ______
2.25% of 180 = ______ Part
3.What % of 30 is 6?
4.$12 is what percent of $48? ÷
5.14 is 20% of what number?
X
6.20% of what number is 34? Whole Percent

17. GUIDED PRACTICE
Directions: Solve each problem using the Percent Pyramid.
Draw out the pyramid for each problem.
1.30% of 90 = __27__
2.25% of 180 = __45__ Part
3.What % of 30 is 6? 20%
4.$12 is what percent of $48? 25% ÷
5.14 is 20% of what number? 70
X
6.20% of what number is 34? 170 Whole Percent

18. STEPS FOR SOLVING PERCENT WORD
PROBLEMS.
1. Read the problem.
2. Determine what the numbers represent.
a. Is the number the: Part, Whole, or Percent
b. This will also help determine what the problem wants
to know.
3. Using the percent pyramid, determine what
operation is necessary to solve the problem.
4. Solve.
5. Ask, “Does this answer make sense?”
There may be another step. BE CAREFUL!

19. STEP 1: READ THE PROBLEM.
When Meyer bought a new stove, he made a
$146 down payment. If the down payment is
25% of the purchase price, what is the cost
of the stove?

20. Step 2: Determine what the numbers represent.
When Meyer bought a new stove, he made a $146 down
payment. If the down payment is 25% of the purchase price,
what is the cost of the stove?
Look back at the key words provided earlier in the PowerPoint.
What does down payment represent?
The Part
•$146 is a down payment, therefore, it is only PART of the
purchase price and will be placed in the top section of the pyramid.
•25 is the percent because it has the % sign; the percent is placed
in the bottom right corner of the pyramid.

21. Step 3: Draw the percent pyramid, and fill it in.
• $146 was the part.
• The percent was also given. part
25%
$146
The pyramid indicates ÷
division is the operation
needed to solve the X 25%
problem.
whole percent
HINT: Don’t forget to change the percent to a decimal!

22. STEP 4 : SOLVING THE PROBLEM
Set up the division:
.25 146
Change the decimal
to a whole number by
moving the decimal If you change the outside
back to the right. number, you have to move
the inside number the same
number of spaces. Then add
zeros to cover the empty
spaces.
Looks like: 25 14600.

23. STEP 4: SOLVING PROBLEM
Divide:
4 5 84
2
25 $14600.
- 125
21 0
- 200
10 0
100
0

24. STEP 5: READ THE PROBLEM AGAIN.
When Meyer bought a new stove, he made a $146 down
payment. If the down payment is 25% of the purchase price,
what is the cost of the stove?
What does the question want to know?
The price of the stove.
Is $584 a reasonable price for a stove?
YES

25. Guided Practice:
Our meal was $39.50, but we got a 20% discount
because our food was late. What did our meal cost after
the discount?
Step 1: Read the problem!
Step 2: Determine what the numbers stand for.
$39.50 was the total cost = whole
20 % = is the percent

26. Step 3: Draw and fill in the
triangle.
?
Notice that you have both
numbers on the bottom of
the triangle. When this
$39.50 20% happens, you simply
multiply.

27. STEP 4: SOLVE THE PROBLEM.
Hint: When solving by hand, you must change the
percent to a decimal by moving the decimal two places
to the left.
$39.50
x .20
7.9000
* Count the number of decimal places in the problem
and move the decimal that many places.

28. STEP 5: DOES THE ANSWER MAKE SENSE?
Always make sure you answered the question.
• Is $7.90 a reasonable answer.
• No, if you were given a 20% discount, $7.90 is more
than half off the price. This does not make sense.
You must subtract the $7.90 from the original cost to find
what you will pay for the meal.
$39.50
- 7.90
$31.60 is the amount paid.

29. 1. During the November special election in Blaine, only 15,400
voters went to the ballot box. If 44,000 registered voters live in
Blaine, what percent of the registered voters cast their votes?
Step 2: 15,400 is part of the voters; 44,000 is the total number of voters which
makes it the whole.
Step 3: Use the pyramid to determine what operation to use.
·35
Step 4: 44,000 ) 15400.00
13200 0
2200 00
15400 2200 00
HINT: Don’t forget to
44,000 ? change the decimal to a
percent.
35%

30. 2. Julia had her car windshield replaced at a cost of $250. After a
$25 deductible is applied, her insurance company will pay 80
percent of the remaining balance. In dollars, how much will the
insurance company pay?
Step 2: $250 is the total cost; $25 is the deductible; and 80 is the percent the
insurance company will pay. Be careful! $250 is not the whole because the 80 is
the percent off the remaining balance after the deductible; therefore, the $250 is
extra information. Find the whole by subtracting the deductible.
$250 – $25 = $225 Step 3: Fill out pyramid.
Step 4: Solve.
$180 $225
x .80
18000
$225 80 % Don’t forget the
decimal. There are 2
decimal places.

31. 3. Mr. and Mrs. Potato Head bought a house five years ago for
95,000. Since then, the value of their home has increased
2%. In dollars, what is the value of their home now?
Step 2: 95,000 is the original amount; 2 is the percent.
Step 3: Fill out pyramid.
Step 4: Solve.
95,000
Step 5: Does $1900.00 make sense
x .02
for the price of a home?
1900.00
No, Add the increase back to the
original cost of the home. 1,900
95,000
+1,900 95,000 2%
$96,900

32. 4. Mr. Buzz took Mr. Woody out for dinner. The cost of their
meal was $32.00. If Mr. Buzz wishes to leave a 15% tip,
how much money should he leave for a tip?
Step 2: $32.00 is the original amount; 15 is the percent off the original amount.
Step 3: Fill out pyramid.
Step 4: Solve.
$32
x.15
160
320 $4.80
HINT: Don’t forget
480 the decimal.
Step 5: Is $4.80 a reasonable $32.00 15%
amount to leave for a tip? YES