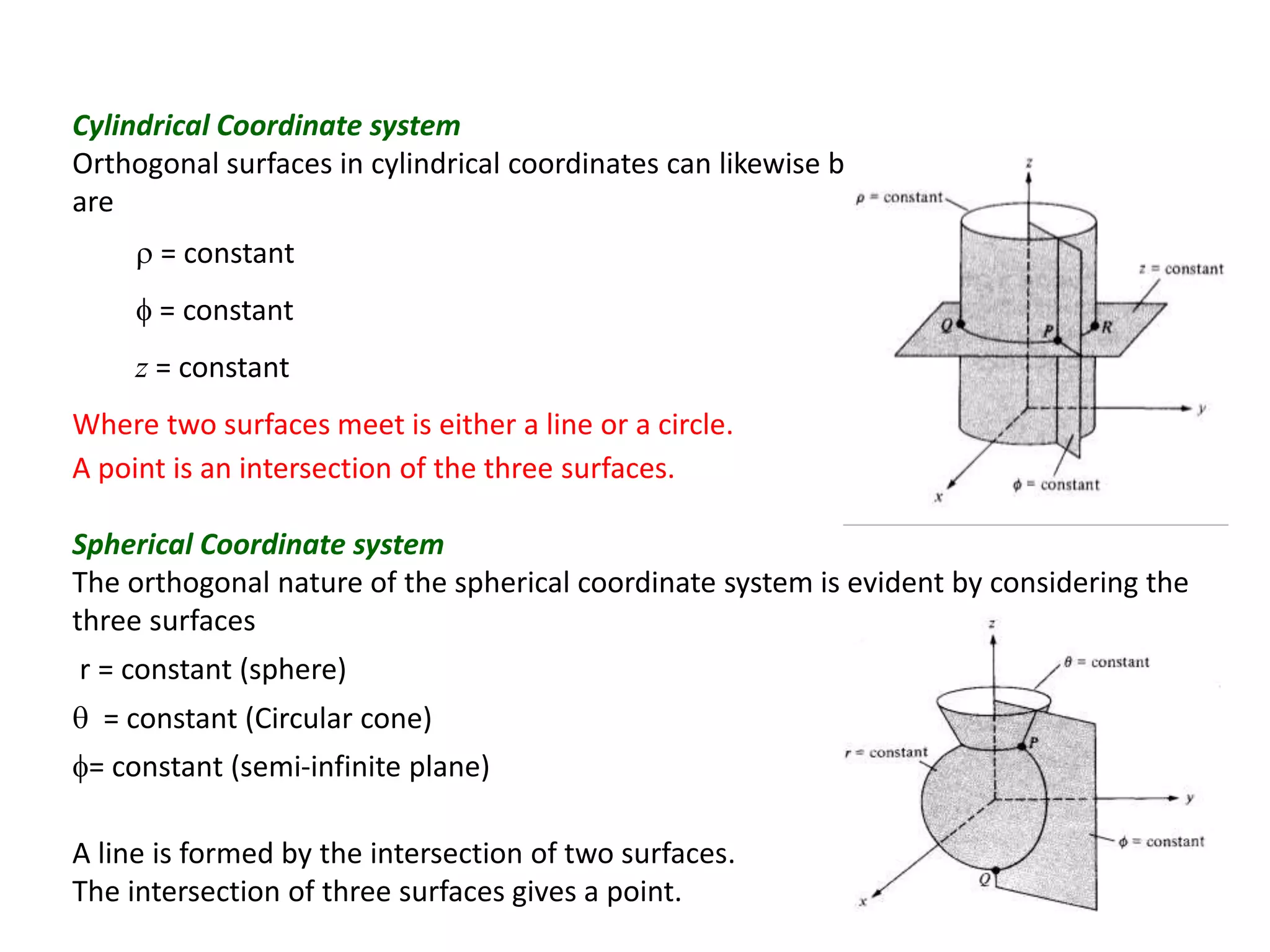
Constant coordinate surfaces can be generated in Cartesian, cylindrical, and spherical coordinate systems by keeping one coordinate constant. In Cartesian coordinates, constant x, y, and z planes intersect to form lines and points. In cylindrical coordinates, constant ρ, φ, and z surfaces intersect to form lines or circles and points. In spherical coordinates, constant r, θ, and φ surfaces intersect to form lines, circular cones, and semi-infinite planes, with points at their intersections. Differential length, area, and volume are also defined differently depending on the coordinate system used.

1. Constant Coordinate Surfaces
and
Differential Length, Area and Volume

2. CONSTANT COORDINATE SURFACES
Surfaces in Cartesian, cylindrical, or spherical coordinate systems are easily
generated by keeping one of the coordinate variables constant and allowing the
other two to vary.
Cartesian Coordinate system
If we keep x constant and allow y and z to vary, an infinite plane is generated.
Thus we could have infinite planes
x = constant
y = constant
z = constant
The intersection of two planes is a line.
For example,
x = constant, y = constant is the line RPQ parallel to the z-axis.
The intersection of three planes is a point.

3. Cylindrical Coordinate system
Orthogonal surfaces in cylindrical coordinates can likewise be generated. The surfaces
are
 = constant
 = constant
z = constant
Where two surfaces meet is either a line or a circle.
A point is an intersection of the three surfaces.
Spherical Coordinate system
The orthogonal nature of the spherical coordinate system is evident by considering the
three surfaces
r = constant (sphere)
 = constant (Circular cone)
= constant (semi-infinite plane)
A line is formed by the intersection of two surfaces.
The intersection of three surfaces gives a point.

4. DIFFERENTIAL LENGTH, AREA, AND VOLUME
Cartesian Coordinate system
Differential displacement is given by
Differential normal area is given by
Differential volume is given by
Differential normal areas in Cartesian coordinates:

5. DIFFERENTIAL LENGTH, AREA, AND VOLUME
Cylindrical Coordinate system
Differential displacement is given by
Differential normal area is given by
Differential volume is given by
Differential normal areas in Cylindrical coordinates:

6. DIFFERENTIAL LENGTH, AREA, AND VOLUME
Spherical Coordinate system
Differential displacement is given by
Differential normal area is given by
Differential volume is given by
Differential normal areas in Spherical coordinates: