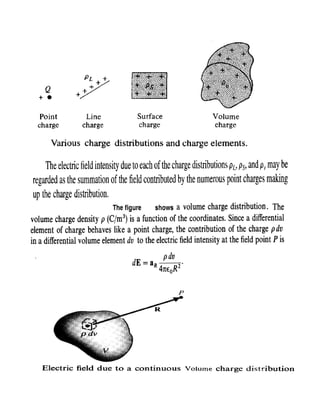
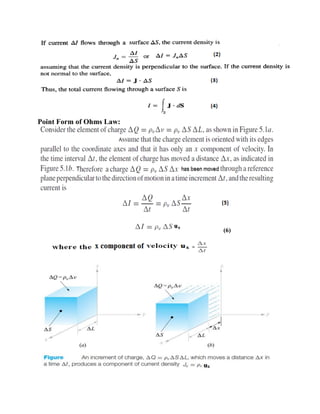
This document provides an overview of electrostatics. It defines key concepts like electric field, electric flux density, Gauss's law, capacitance, and more. Applications of electrostatics include electric power transmission, X-ray machines, solid-state electronics, medical devices, industrial processes, and agriculture. Coulomb's law describes the electric force between point charges. Gauss's law relates the electric flux through a closed surface to the enclosed charge. Capacitance is the ratio of stored charge on conductors to the potential difference between them.

1. UNIT II
ELECTROSTATICS
Electric field, Coulomb's law, Gauss's law and applications, Electric potential, Conductors in static
electric field, Dielectrics in static electric field, Electric flux density and dielectric constant,
Boundary conditions, Capacitance, Parallel, cylindrical and spherical capacitors, Electrostatic
energy, Poisson's and Laplace's equations, Uniqueness of electrostatic solutions, Current density
and Ohm's law, Electromotive force and Kirchhoff's voltage law, Equation of continuity and
Kirchhoff's current law
INTRODUCTION
An electrostatic field is produced by a static charge distribution. In electrostatics,
electric charges (the sources) are at rest and electric fields do not change with time. Electric
power transmission, X-ray machines, and lightning protection are associated with strong electric
fields and will require a knowledge of electrostatics to understand and design suitable equipment.
The devices used in solid-state electronics are based on electrostatics. These include resistors,
capacitors, and active devices such as bipolar and field effect transistors, which are based on
control of electron motion by electrostatic fields. Almost all computer peripheral devices like
Touch pads, capacitance keyboards, cathode-ray tubes, liquid crystal displays, and electrostatic
printers are typical examples that are based on electrostatic fields. In medical work, diagnosis is
often carried out with the aid of electrostatics, as incorporated in electrocardiograms,
electroencephalograms, and other recordings of organs with electrical activity including eyes, ears,
and stomachs. In industry, electrostatics is applied in a variety of forms such as paint spraying,
electrodeposition, electrochemical machining, and separation of fine particles. Electrostatics is
used in agriculture to sort seeds, direct sprays to plants, measure the moisture content of crops,
spin cotton, and speed baking of bread.
2.1 COULOMB'S LAW:
Coulomb's law deals with the force a point charge exerts on another point charge. A point charge
means a charge that is located on a body whose dimensions are much smaller than other relevant
dimensions. Charges are generally measured in coulombs(C). One coulomb is approximately
equivalent to 6 x 1018
electrons; it is a very large unit of charge because one electron charge e =
-1.6019 X 10-19
C.

3. The important noteworthy points are as follows:
(7.a)

4. PRINCIPLE OF SUPERPOSITION:
2.2 ELECTRIC FIELD INTENSITY

5. Consider one charge fixed in position, say Q1, and move a second charge
slowly around. There exists everywhere a force on this second charge. In other
words, this second charge is displaying the existence of a force field that is
associated with charge, Q1. This second charge a known as test charge Qt . The
force on it is given by Coulomb’s law,
The electric field of a single point charge becomes:

6. Electric Field Intensity in rectangular coordinates:
Fig 3:Electric Field Intensity In rectangular coordinates

7. Electric Field Intensity Due to n Point Charges (Principle of
Superposition):

8. and the distance vector is given by
Electric Fields Due To Continuous Charge Distributions

10. FIELD OF A LINE CHARGE (or)
⮚ Consider a straight-line charge extending along the z axis in a
cylindrical coordinate system from −∞ to ∞, as shown
in Figure. Let the uniform line charge density be 𝜌𝐿. It is desired to
find the electric field intensity E at any and every point resulting from the line.
⮚ Symmetry should always be considered first in order to determine two specific
factors: (1) with which coordinates the field does not vary, and (2) which
components of the field are not present.

11. ● Moving around the line charge, varying ϕ while keeping ρ and z constant, the
line charge appears the same from every angle. Azimuthal symmetry is
present and no field component varies with ϕ.
● Again maintaining ρ and ϕ constant while moving up and down the line charge
by changing z, the line charge still recedes into infinite distance in both
directions and the problem is unchanged. This is axial symmetry and leads to
fields that are not functions of z.
● Maintaining ϕ and z constant, varying ρ leads to changes in the problem and
hence the field varies only with ρ.
●
● No element of charge produces a ϕ component of electric field intensity; E ϕ
is zero.

12. ● However, each element does produce an Eρ and an Ez component, but the
contribution to Ez by elements of charge that are equal distances above and
below the point at which the field has to be determining will cancel.
⮚ Only Eρ component will exist and it varies only with ρ.

14. The above equation shows that the Electric field intensity falls off inversely with the distance to
the charged line.
FIELD OF A SHEET OF CHARGE (or)
Fig: Circular Sheet of charge

16. From the figure ,
Hence equation (6) can be rewritten as
CASE:
ELECTRIC FIELD DUE TO INFINITE SHEET OF CHARGE

17. Where az is the unit vector, which is normal to the sheet and directed outward, or away from it.
The electric field is independent of the distance between the sheet and the point of observation P.
⮚ In a parallel plate capacitor, the electric field existing between the two plates having
equal and opposite charges is given by
ELECTRIC FLUX DENSITY
Electric Flux:
Electric Flux Density:
The electric flux density D is measured in coulombs per square meter. The direction
of D at a point is the direction of the flux lines at that point, and the magnitude is
given by the number of flux lines crossing a surface normal to the lines divided by
the surface area.
Figure : The electric flux in the region between a pair of charged concentric spheres.

18. Let us consider an inner sphere of radius a and an outer sphere of radius b, with
charges of Q and −Q, respectively (Figure ). The paths of electric flux ψ extending
from the inner sphere to the outer sphere are indicated by the symmetrically
distributed streamlines drawn radially from one sphere to the other.

19. GAUSS'S LAW AND APPLICATIONS
GAUSS'S LAW:
Gauss's law constitutes one of the fundamental laws of electromagnetism.
Gauss's law states that the total electric flux ψ passing through any closed surface is equal
to the total charge enclosed by that surface.
Ψ=Qenc Coulombs
Let us imagine a distribution of charge, shown as a cloud of point charges in Figure,
surrounded by a closed surface of any shape. If the total charge is Q, then Q
coulombs of electric flux will pass through the enclosing surface. At every point on
the surface the electric-flux-density vector D will have some value DS, where the
subscript S indicates that D must be evaluated at the surface. Consider an incremental
element of the surface ΔS. The incremental surface element is a vector quantity.
The resultant integral is a closed surface integral involving two coordinates.
The closed surface over which the integration is to be performed is called a Gaussian surface
The mathematical formulation of Gauss’s law is given by ,

20. The above equation is the integral form of Gauss Law.
The Differential or Point Form Of Gauss's Law:
Gauss’s law may be written in terms of the charge distribution as,
(1)
By applying divergence theorem to the middle term of above equation,
(2)
Comparing the two volume integrals in eqns (1) and (2) gives
(3)
The above equation is the differential or point form of Gauss's law. It states that the
volume charge density is the same as the divergence of the electric flux density.
Gaussian Surface :
It is any physical or imaginary closed surface around a charge which satisfies the following
condition.
1. D is everywhere either normal or tangential to the closed surface, so that D · dS becomes
either D dS or zero, respectively.
2. On that portion of the closed surface for which D · dS is not zero, D = constant.
Proof of Gauss law:

21. Fig: Proof of Gauss law
APPLICATIONS OF GAUSS'S LAW:
1) Electric field intensity due to line charge: Consider an infinite line charge placed
along z-axis. Consider a small length ‘L of the line charge.

23. 2) Electric field intensity due to infinite sheet of charge

24. 3) Field due to Co-axial Cable
Consider two co-axial cylindrical conductors with inner radius ‘a’ and outer radius ‘b’ each infinite
in extent.

25. POTENTIAL DIFFERENCE
Work done in moving a charge Q from one point to another in electric field E is,
Potential difference is the work done per unit charge in moving a unit positive charge from one point to
another in an electric field.
POTENTIAL DIFFERENCE FOR A POINT CHARGE
The differential length is given by

26. POTENTIAL/ABSOLUTE POTENTIAL/POTENTIAL FIELD OF A POINT CHARGE
Potential at a point is defined as work done in moving a unit positive charge from infinity to the
field point.
RELATIONSHIP BETWEEN E AND V

27. POTENTIAL AND ELECTRIC FIELD DUE TO DIPOLE
A pair of equal and opposite charges separated by a small distance is known as electric dipole.
Fig:Dipole

29. CAPACITANCE
Consider two conductors M1 and M2 separated by a dielectric medium with permittivity ε as shown
in Fig . Conductor M2 carries a total positive charge Q, and M1 carries an equal negative charge.
There are no other charges present, and the total charge of the system is zero. The charge is carried
on the surface as a surface charge density and also that the electric field is normal to the conductor
surface. Each conductor is, moreover, an equipotential surface. Because M2 carries the positive
charge, the electric flux is directed from M2 to M1, and M2 is at the more positive potential. In
other words, work must be done to carry a positive charge from M1 to M2.Let us designate the
potential difference between M2 and M1 as V0.
The capacitance of this two-conductor system is defined as the ratio of the magnitude
of the total charge on either conductor to the magnitude of the potential difference between
conductors,
Capacitance is measured in farads (F), where a farad is defined as one coulomb per volt. The
capacitance is a function only of the physical dimensions of the system of conductors and of the
permittivity of the homogeneous dielectric. The capacitance is independent of the potential and
total charge, for their ratio is constant. If the charge density is increased by a factor of N, Gauss’s
law indicates that the electric flux density or electric field intensity also increases by N, as does
the potential difference.

30. PARALLEL-PLATE CAPACITOR
Consider a two-conductor system in which the conductors are identical, infinite parallel planes
with separation d as shown in the fig . The lower conducting plane or plate is at at z = 0 and the
upper plate is at z = d. Let the lower plate has a uniform charge density +ρs and upper plate has
-ρs.
Fig: Parallel-Plate Capacitor

31. Electric field intensity at any point in-between the plates is,
The potential difference between the plates is,

32. CYLINDRICAL CAPACITOR:
This is essentially a coaxial cable or coaxial cylindrical capacitor. Consider length L of two
coaxial conductors of inner radius a and outer radius b (b > a) as shown in Figure . Let the space
between the conductors be filled with a homogeneous dielectric with permittivity ε.
Hence the charge Q is given by

33. Spherical Capacitor/ Capacitance between Two Spherical Shells:
This is the case of two concentric spherical conductors. Consider a spherical capacitor with the
inner sphere of radius a and outer sphere of radius b (b> a) separated by a dielectric medium with
permittivity ε as shown in Figure .
Fig: Spherical capacitor

34. Case1: Capacitance of an isolated sphere
Consider an isolated sphere of radius ‘a’ with a charge +Q.

35. Fig:A parallel-plate capacitor containing two dielectrics
The potential difference between the plates with two dielectrics is given by,V
At dielectric interface, D1 = D2 = D

37. i) Series connection of Capacitors:

38. ii) Parallel connection of Capacitors:

40. Substituting in Equation (6),
The above equation can be alternatively given as,

41. Energy stored in the electrostatic field of a capacitor:

42. POISSON'S AND LAPLACE'S EQUATIONS
Problems involving one to three dimensions can be solved either analytically
or numerically. Laplace’s and Poisson’s equations, when compared to other
methods, are probably the most widely useful because many problems in
engineering practice involve devices in which applied potential differences are
known, and in which constant potentials occur at the boundaries.

44. GENERAL PROCEDURE FOR SOLVING POISSON'S OR LAPLACE'S
EQUATION
Capacitance using Laplace Equation:
1. Capacitance of a Parallel Plate Capacitor:

45. Fig: Parallel plate capacitor
Using boundary condition in eqn(4) results in
Substituting Eqn (5) and Eqn (6) in Eqn(1) yields,

46. Substituting Eqn (7) in Eqn(8) gives,
Equation (14) is the capacitance of a Parallel Plate Capacitor.
2. Capacitance of a Coaxial Cylinder/Coaxial Cable

47. Integrating once,
From Eqn (2) ,

48. Substituting Eqn (5) and Eqn (6) in Eqn(1) yields,
Substituting Eqn (7) in Eqn(8) gives,
(The Second term of Eqn.(7) has not been considered for it is not a function of r)
The electric Flux density is given by,
Substituting Eqn (10) in Eqn(11) gives,

49. Substituting Eqn.(15) in eqn(16) gives,
Equation (17) is the capacitance of a coaxial cylinder/coaxial cable.
3. Capacitance of a Spherical Capacitor/ Capacitance
between two Spherical shells/ Capacitance between two
conducting spheres:
Consider two spherical shells separated by a dielectric of permittivity ε. Let
“a” be the radius of the inner shell and “b” be the radius of the inner shell.
Fig: Spherical Capacitor

50. Integrating the above equation once,
Integrating again,
Substituting the boundary in eqn(6) results in,

51. Substituting Eqn (10) and Eqn (11) in Eqn(6) yields,
Substituting Eqn (12) in Eqn(13) yields,
(The Second term of Eqn.(12) has not been considered for it is not a function of r)
The electric Flux density is given by,
Substituting Eqn.(14) in eqn(15) gives,

52. Case1: Capacitance of an isolated sphere
Consider an isolated sphere of radius ‘a’ with a charge +Q.

53. UNIQUENESS OF ELECTROSTATIC SOLUTIONS:
There are several methods of solving a given problem such as analytical,
graphical, numerical, experimental, etc., There arises a doubt whether solving
Laplace's equation in different ways gives different solutions. However there is only
one solution and that solution is unique.
The theorem applies to any solution of Poisson's or Laplace's equation in a given
region or closed surface.
The theorem is proved by contradiction. It is assumed that there are two solutions
V1 and V2 of Laplace's equation both of which satisfy the prescribed boundary
conditions. Thus

54. Applying divergence theorem to the R.H.S of eq.(7) results in
This is the uniqueness theorem: If a solution to Laplace's equation can be
found that satisfies the boundary conditions, then the solution is unique.
CURRENT DENSITY AND OHM'S LAW
Current(I):Electric charges in motion constitute a current. The current (in amperes) through a
given area is the electric charge passing through the area per unit time. Current is symbolized by I
, and therefore

55. (1)
The unit of current is the ampere (A),defined as a rate of movement of charge passing a given
reference point (or crossing a given reference plane) of one coulomb per second.
:
Current density (J), measured in amperes per square meter (A/m2
), is a vector .

56. Point Form of Ohms Law:
(6)

57. In terms of current density,
(7)
(10)
Using the relations
and ,
The convection current density is given by,
(11)

58. Ohm’s law and the metallic conductors are also described as isotropic, or having
the same properties in every direction.

59. The above equation is known as Ohms law.
ELECTROMOTIVE FORCE AND KIRCHHOFF'S VOLTAGE LAW

62. EQUATION OF CONTINUITY AND KIRCHHOFF'S CURRENT LAW
This is the integral form of continuity equation.