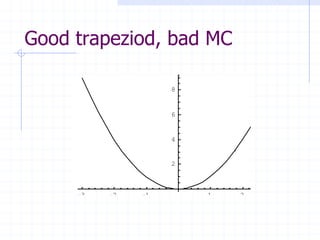
This document discusses Monte Carlo and quasi-Monte Carlo integration methods. It explains that while classical integration rules like the trapezoid rule become less accurate in higher dimensions, Monte Carlo integration maintains the same error rate regardless of dimension. Quasi-Monte Carlo sequences can converge even faster than Monte Carlo, though the rate depends on the specific sequence used. The document provides examples of integration methods and sequences, and discusses factors that affect the performance and accuracy of Monte Carlo, quasi-Monte Carlo, and lattice rule integration techniques.

1. Monte Carlo and
quasi-Monte Carlo Integration
John D. Cook
M. D. Anderson Cancer Center
July 24, 2002

2. Trapezoid rule in one dimension
Error bound proportional to product of
 Step size squared
 Second derivative of integrand
N = number of function evaluations
Step size h = N-1
Error proportional to N-2

3. Simpson’s rule in one dimensions
Error bound proportional to product of
 Step size to the fourth power
 Fourth derivative of integrand
Step size h = N-1
Error proportional to N-4
All bets are off if integrand doesn’t have
a fourth derivative.

4. Product rules
In two dimensions, trapezoid error
proportional to N-1
In d dimensions, trapezoid error
proportional to N-2/d.
If 1-dimensional rule has error N-p,
n-dimensional product has error N-p/d

5. Dimension in a nutshell
Assume the number of integration
points N is fixed, as well as the order of
the integration rule p.
Moving from 1 dimension to
d dimensions divides the number of
correct figures by d.

6. Monte Carlo to the rescue
Error proportional to N-1/2,
independent of dimension!
Convergence is slow, but doesn’t get
worse as dimension increases.
Quadruple points to double accuracy.

7. How many figures can you get
with a million integration points?
Dimension Trapezoid Monte Carlo
1 12 3
2 6 3
3 4 3
4 3 3
6 2 3
12 1 3

8. Fine print
Error estimate means something
different for product rules than for MC.
Proportionality factors other than
number of points very important.
Different factors improve performance
of the two methods.

9. Interpreting error bounds
Trapezoid rule has deterministic error
bounds: if you know an upper bound on
the second derivative, you can bracket
the error.
Monte Carlo error is probabilistic.
Roughly a 2/3 chance of integral being
within one standard deviation.

10. Proportionality factors
Error bound in classical methods
depends on maximum of derivatives.
MC error proportional to variance of
function, E[f2] – E[f]2

11. Contrasting proportionality
Classical methods improve with smooth
integrands
Monte Carlo doesn’t depend on
differentiability at all, but improves with
overall “flatness”.

12. Good MC, bad trapezoid
1
0.8
0.6
0.4
0.2
1.5 2 2.5 3

13. Good trapeziod, bad MC
8
6
4
2
-3 -2 -1 1 2 3

14. Simple Monte Carlo
If xi is a sequence of independent samples from
a uniform random variable

15. Importance Sampling
Suppose X is a random variable with PDF and xi is a
sequence of independent samples from X.

16. Variance reduction (example)
If an integrand f is well approximated by a PDF that is
easy to sample from, use the equation
and apply importance sampling.
Variance of the integrand will be small, and so
convergence will be fast.

17. MC Good news / Bad news
MC doesn’t get any worse when the
integrand is not smooth.
MC doesn’t get any better when the
integrand is smooth.
MC converges like N-1/2 in the worst
case.
MC converges like N-1/2 in the best case.

18. Quasi-random vs. Pseudo-random
Both are deterministic.
Pseudo-random numbers mimic the
statistical properties of truly random
numbers.
Quasi-random numbers mimic the
space-filling properties of random
numbers, and improves on them.

19. 120 Point Comparison
1 .0 1 .0
0 .8 0 .8
0 .6 0 .6
0 .4 0 .4
0 .2 0 .2
0 .0 0 .0
0 .0 0 .2 0 .4 0 .6 0 .8 1 .0 0 .0 0 .2 0 .4 0 .6 0 .8 1 .0
Sobol’ Sequence Excel’s PRNG

20. Quasi-random pros and cons
The asymptotic convergence rate is more like
N-1 than N-1/2.
Actually, it’s more like log(N)dN-1.
These bounds are very pessimistic in practice.
QMC always beats MC eventually.
Whether “eventually” is good enough
depends on the problem and the particular
QMC sequence.

21. MC-QMC compromise
Randomized QMC
Evaluate integral using a number of randomly
shifted QMC series.
Return average of estimates as integral.
Return standard deviation of estimates as
error estimate.
Maybe better than MC or QMC!
Can view as a variance reduction technique.

22. Some quasi-random sequences
Halton – bit reversal in relatively prime
bases
Hammersly – finite sequence with one
uniform component
Sobol’ – common in practice, based on
primitive polynomials over binary field

23. Sequence recommendations
Experiment!
Hammersley probably best for low
dimensions if you know up front how many
you’ll need. Must go through entire cycle or
coverage will be uneven in one coordinate.
Halton probably best for low dimensions.
Sobol’ probably best for high dimensions.

24. Lattice Rules
Nothing remotely random about them
“Low discrepancy”
Periodic functions on a unit cube
There are standard transformations to
reduce other integrals to this form

25. Lattice Example

26. Advantages and disadvantages
Lattices work very well for smooth integrands
Don’t work so well for discontinuous
integrands
Have good projections on to coordinate axes
Finite sequences
Good error posterior estimates
Some a priori estimates, sometimes
pessimistic

27. Software written
QMC integration implemented for
generic sequence generator
Generators implemented: Sobol’,
Halton, Hammersley
Randomized QMC
Lattice rules
Randomized lattice rules

28. Randomization approaches
Randomized lattice uses specified lattice size,
randomize until error goal met
RQMC uses specified number of
randomizations, generate QMC until error
goal met
Lattice rules require this approach: they’re
finite, and new ones found manually.
QMC sequences can be expensive to compute
(Halton, not Sobol) so compute once and
reuse.

29. Future development
Variance reduction. Good
transformations make any technique
work better.
Need for lots of experiments.

30. Contact
http://www.JohnDCook.com