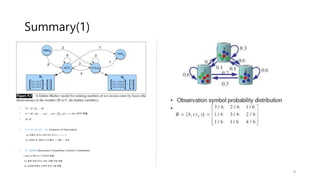
1. Hidden Markov Models (HMMs) are used to model sequential data where the underlying process generating the observable outputs is not visible but assumed to be a Markov process with hidden states.
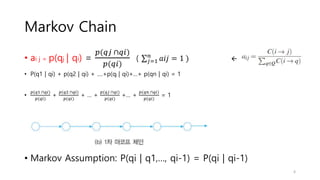
2. HMMs define transition probabilities between hidden states and emission probabilities of observable outputs for each state.
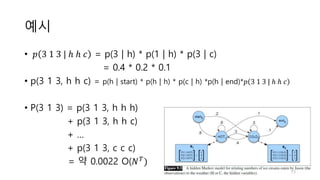
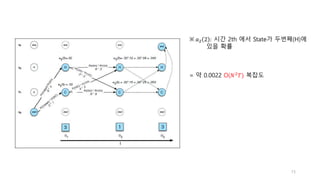
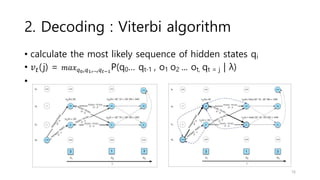
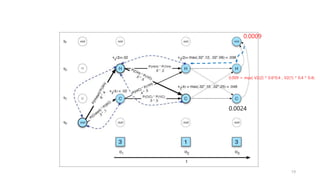
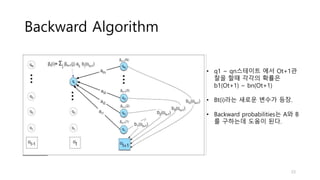
3. There are three typical problems for HMMs: likelihood computation, decoding the most likely sequence of hidden states, and learning the transition and emission probabilities from data.

















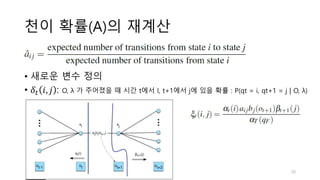
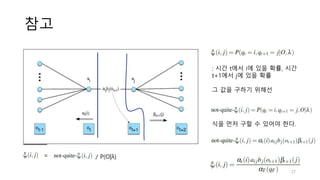

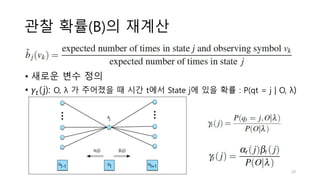





![• [Rabiner, 1986] L. Rabiner and B. Juang, “An Introduction to
Hidden Markov Models,” Proc. IEEE ASSP Magazine, 1986.
Reference
35](https://image.slidesharecdn.com/hiddenmarkovmodelexplained-210417090441/85/Hidden-markov-model-explained-35-320.jpg)