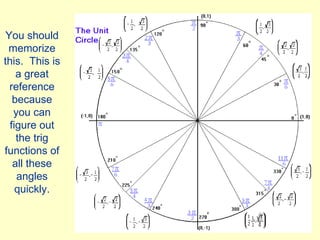
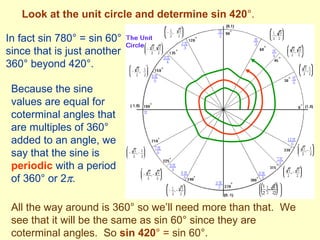
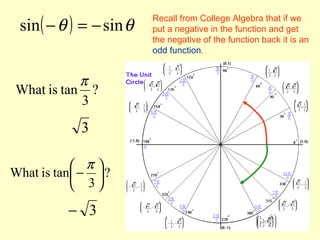
The document defines trigonometric functions using the unit circle. It shows that the sine of an angle is equal to the y-coordinate of the point on the unit circle where the terminal side of the angle intersects, while the cosine is equal to the x-coordinate. The tangent is defined as the ratio of the sine to the cosine. Key properties discussed include the periodic nature of the trig functions with periods of 360 degrees or 2π radians, and whether functions are even or odd based on their behavior under negative inputs.