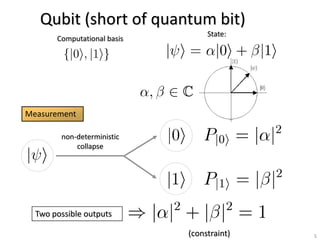
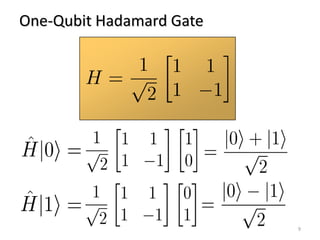
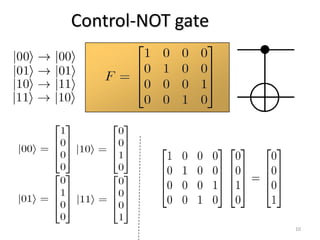
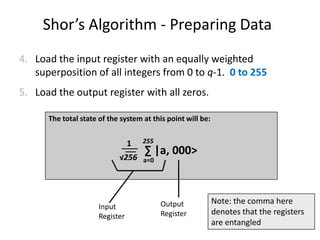
Shor's algorithm is a quantum algorithm developed in 1994 that efficiently factors large integers, demonstrating the vulnerability of RSA encryption. It operates in polynomial time using principles like modular arithmetic and quantum Fourier transform, vastly outperforming classical methods. Recent advancements have successfully implemented Shor's algorithm on small-scale quantum computers, achieving factorization of numbers like 15, 21, and 143.

1. Shor’s Algorithm
University Of Calcutta
MRINAL KANTI MONDAL

2. Introduction
 “I
think I can safely say that nobody
understands quantum mechanics” - Feynman
 1982 - Feynman proposed the idea of creating
machines based on the laws of quantum
mechanics instead of the laws of classical
physics.
 1985 - David Deutsch developed the quantum Turing machine,
showing that quantum circuits are universal[1].
 1994 - Peter Shor came up with a quantum algorithm to factor
very large numbers in polynomial time.
1997 - Lov Grover develops a quantum search algorithm with
O(√N) complexity.

3. Background
• It is a Quantum algorithm, to find the prime factors of
any given integer N.
• Formulated and named after mathematician Peter Shor
in 1994.
• It takes time O((log N)3). Which demonstrates that an
integer factorization can be solved in a quantum
computer in polynomial time.
• It makes RSA vulnerable to attack, as RSA is based on
the assumption that factoring large numbers is
computationally infeasible.
3

4. Quantum computation
• In quantum computing single particle’s actual state is not
restricted to only one of the two observable states.
• When observed or measured, the particle will manifest
itself in one observable state or the other with respective
probability encoded in the superposition.
• Any state of the system is modeled by a unit-length vector
in the Hilbert space C2n.
4

5. Qubit (short of quantum bit)
Computational basis
State:
Measurement
non-deterministic
collapse
Two possible outputs
(constraint)
5

6. Multi-qubit Systems
2-qubit QC:
N-qubit
quantum computer
states
6

7. Entangled states
2-qubit
system
Entangled state
Example:
7

8. Quantum gates
NOT Gate (Bit Flip)
8

9. One-Qubit Hadamard Gate
9

10. Control-NOT gate
10

11. Significance of Shor’s algorithm
• Fast factorization of any given no.
• Finding a factor of a n-bit integer requires
exp( (n^1/3(log n)^2/3) operations using best classical
algorithm.
• Shor’s algorithm can accomplish this same task using
O(n^2(log n(log log n)) operations.
• i.e. a quantum computer can factor a number in
exponentially faster than the best known classical
algorithm.
11

12. Shor’s Algorithm
Shor’s algorithm shows (in principle,) that a quantum
computer is capable of factoring very large numbers in
polynomial time.
The algorithm is dependant on
Modular Arithmetic
Quantum Parallelism
Quantum Fourier Transform

13. The algorithm
• The problem is: given an odd composite number N,
find and integer d, strictly between 1 and N, that
divides N.
• The Shor’s algorithm consists of two parts:1. Conversion of the problem of factoring to the
problem of finding the period.(this part can be
implemented classically).
2. Finding the period (Quantum period finding) using
the quantum Fourier transform, and is responsible
for quantum speedup.
13

14. Classical part
1. A random number a<N picked.
2. Compute gcd(a, N). This may be done using the Euclidean
algorithm.
3. If gcd(a,N)≠1, then there is a nontrivial factor of N.
4. f(x + r) = ax + r mod N = ax mod N=f(x).
5. If r is odd, go to step 1.
6. If a r/2 -1 (mod N), go back to step 1.
7. gcd(a r/2 ± 1, N) is a non trivial factor of N.
14

15. Shor’s Algorithm - Periodicity
 An important result from Number Theory:
a
F(a) = x mod N is a periodic function
 Choose N = 15 and x = 7 and we get the following:
70 mod 15 = 1
71 mod 15 = 7
72 mod 15 = 4
3
7 mod 15 =13
4
7 mod 15 = 1
.
.
.

16. Shor’s Algorithm - In Depth Analysis
To Factor an odd integer N (Let’s choose N=15) :
2
1. Choose an integer q such that N < q < 2N
2
let’s pick 256
2. Choose a random integer x such that GCD(x, N) = 1 let’s pick 7
3. Create two quantum registers (these registers must also be
entangled so that the collapse of the input register
corresponds to the collapse of the output register)
•
Input register: must contain enough qubits to represent
numbers as large as q-1. up to 255, so we need 8 qubits
•
Output register: must contain enough qubits to represent
numbers as large as N-1. up to 14, so we need 4 qubits

17. Shor’s Algorithm - Preparing Data
4. Load the input register with an equally weighted
superposition of all integers from 0 to q-1. 0 to 255
5. Load the output register with all zeros.
The total state of the system at this point will be:
1
255
∑ |a, 000>
√256 a=0
Input
Register
Output
Register
Note: the comma here
denotes that the registers
are entangled

18. Shor’s Algorithm - Modular Arithmetic
6. Apply the transformation x a mod N to each number in the
input register, storing the result of each computation in the
output register.
Input Register
7a Mod 15
Output Register
|0>
70 Mod 15
1
|1>
71 Mod 15
7
|2>
7 Mod 15
4
|3>
73 Mod 15
13
|4>
74 Mod 15
1
|5>
75 Mod 15
7
|6>
76 Mod 15
4
|7>
77 Mod 15
13
2
.
.

19. Shor’s Algorithm - Superposition
Collapse
7. Now take a measurement on the output register. This will
collapse the superposition to represent just one of the
results of the transformation, let’s call this value c.
Our output register will collapse to represent one of the
following:
|1>, |4>, |7>, or |13>
For sake of example, lets choose |1>

20. Shor’s Algorithm - Entanglement
8. Since the two registers are entangled, measuring the
output register will have the effect of partially collapsing
the input register into an equal superposition of each
state between 0 and q-1 that yielded c (the value of the
collapsed output register.)
Since the output register collapsed to |1>, the input register will partially collapse to:
1
√64
|0> +
1
|4> +
√64
1
√64
1
|8> +
1
|12>, . . .
√64
The probabilities in this case are 64 since our register is now in an equal superposition
of 64 values (0, 4, 8, . . . 252)

21. Shor’s Algorithm - QFT
We now apply the Quantum Fourier transform on the
partially collapsed input register. The Fourier transform
has the effect of taking a state |a> and transforming it
into a state given by: 1 q-1
2iac / q
√q
1
√64
∑ |c> *e
c=0
∑ |a> ,|1>
aA
1
√256
255
∑ |c> *e
2iac / 256
c=0
Note: A is the set of all values that 7 a mod 15 yielded 1. In our case A = {0,
4, 8, …, 252}
So the final state of the input register after the QFT is:
255
2iac / 256
1
1
∑
∑ |c> *e
√64 a  A √256 c=0
, |1>

22. Shor’s Algorithm - QFT
The QFT will essentially peak the probability amplitudes at
integer multiples of q/4 in our case 256/4, or 64.
|0>, |64>, |128>, |192>, …
So we no longer have an equal superposition of states, the
probability amplitudes of the above states are now higher
than the other states in our register. We measure the
register, and it will collapse with high probability to one of
these multiples of 64, let’s call this value p.
With our knowledge of q, and p, there are methods of
calculating the period (one method is the continuous
fraction expansion of the ratio between q and p.)

23. Shor’s Algorithm - The Factors
10. Now that we have the period, the factors of N can be
determined by taking the greatest common divisor of
N with respect to x ^ (P/2) + 1 and
x ^ (P/2) - 1. The idea here is that this computation
will be done on a classical computer.
We compute:
Gcd (7
Gcd (7
4/2
+ 1, 15) = 5
4/2
- 1, 15) = 3
Successfully factored 15!

24. Shor’s Algorithm - Problems
 The QFT comes up short and reveals the wrong period.
This probability is actually dependant on your choice of q.
The larger the q, the higher the probability of finding the
correct probability.
 The period of the series ends up being odd.
If either of these cases occur, we go back to the
beginning and pick a new x.
Quantum modular exponentiation, much slower than the
quantum Fourier transform.

25. Applications
• Factoring – RSA encryption.
• Quantum simulation.
• Spin-off technology – spintronics, quantum cryptography.
• Spin-off theory – complexity theory, DMRG theory, Nrepresent ability theory.
25

26. Recent works on Shor’s algorithm
• In 2001, a 7 qubit machine was built and
programmed to run Shor’s algorithm to successfully
factor 15, but no entanglement is observed.
• In 2012, the factorization of 21 was achieved.
• In April 2012, the factorization of 143 was achieved.
26

27. Reference:
• Peter W. Shor “Polynomial-Time Algorithms for Prime Factorization
and Discrete Logarithms on a Quantum Computer “, SIAM Journal
on Computing (1997).
• Michael A. Nielsen & Isaac Chuang, ‘Quantum computation and
quantum information’, Cambridge university press.
• Quantum Computing Explained - D. McMahon , (Wiley, 2007) .
• An introduction to Quantum Computing - Oxford University Press,
Jan,2007.
• www.eecis.udel.edu/~saunders/courses/879-03s/
• http://www.cs.berkeley.edu/~vazirani/
27

28. Thank you
28