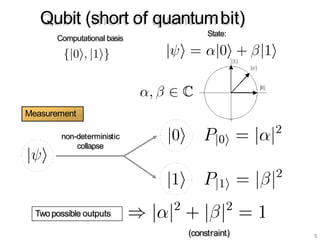
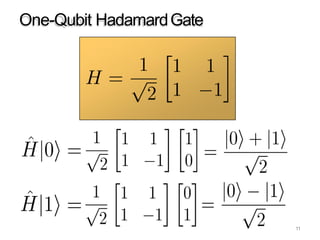
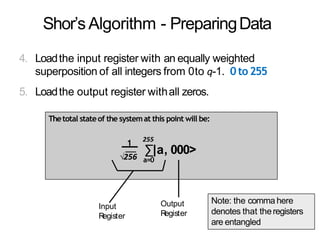
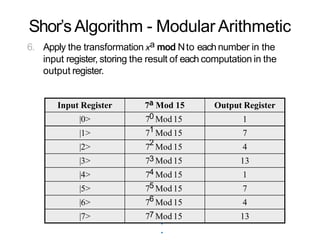
The document discusses the fundamentals of quantum computing, focusing on the historical development of quantum algorithms, particularly Shor's algorithm for factoring large integers, which poses a potential threat to current internet encryption methods like RSA. It explains how quantum mechanics principles such as superposition and entanglement enable quantum computers to factor numbers more efficiently than classical algorithms. Recent advancements in quantum computing applications are also highlighted, showcasing significant achievements in factorization using quantum machines.

1. Basics of Quantum
Computing
Presented By: Utkarsh Patel

2. Introduction
▪“I think I can safely saythat nobody
understands quantum mechanics” - Feynman
▪1982 - Feynman proposed the idea ofcreating
machines based on the laws of quantum
mechanics instead of the laws of classical
physics.
▪1985 - David Deutsch developed the quantum Turingmachine,
showing that quantum circuits areuniversal[1].
▪1994 - Peter Shorcame up with aquantum algorithm tofactor
very large numbers in polynomialtime.
▪1997 - LovGrover develops aquantum searchalgorithm with
O(√N) complexity.

3. • Much of the encryption over the internet relies on one
numerical phenomenon that its really hard to take on a
big number and find its factors.
• The classical method to do that is quite slow and non-
feasible.
• The internet is thus secured for now.
• Use of quantum computing can however change that and
pose a big threat to internet security.
Introduction

4. 4
Background
• It is aQuantum algorithm, to find the prime factors of
any given integer N.
• Formulated and named after mathematician PeterShor
in 1994.
• It takes time O((log N)3). Which demonstrates thatan
integer factorization canbe solved in aquantum
computer in polynomialtime.
• It makesRSAvulnerable to attack, asRSAis basedon
the assumption that factoring large numbers is
computationally infeasible.

5. • Bob chooses two primes p,q and compute n=pq.
• ψ(n)=(p-1)*(q-1).
• Bob chooses e (such that 1<e<ψ(n)) with
gcd(e, ψ(n))=1.
• Now, Bob chooses d such that ed-x*ψ(n)=1.
• Bob makes (n,e) public and (p,q,d) secret.
• Alice encrypts M(message) as C≡Me (mod n).
• Bob decrypts by computing M≡Cd (mod n).
The RSA Algorithm

6. 6
Quantum computation
• In quantum computing single particle’s actual state isnot
restricted to only one of the two observable states.
• When observed or measured, the particle will manifest
itself in one observable state or the other with respective
probability encoded in thesuperposition.
• Any state of the system ismodeled by aunit-length vector
in the Hilbert space.

7. Qubit (short of quantumbit)
5
Computational basis
State:
Measurement
non-deterministic
collapse
Twopossible outputs
(constraint)

8. Multi-qubit Systems
2-qubitQC:
N-qubit
quantumcomputer states
8

9. Entangledstates
2-qubit
system
Entangled state
Example:
9

10. Quantum gates
NOTGate (Bit Flip)
10

11. One-Qubit HadamardGate
11

12. Shor’s Algorithm
• Developed by Peter Shor, this algorithm attempts to
find the factors of the big number by taking help of
quantum mechanics.
• It exploits the properties of quantum superposition,
entanglement and quantum Fourier transform.
• Well, on a broad level shor’s algorithm starts with a
crappy guess that might share a factor with our
number. Then, the algorithm transforms it into a much
better guess that probably does share a factor.

13. Significance of Shor’salgorithm
• Fastfactorization of any givenno.
• Finding afactor of an-bit integerrequires
exp( (n^1/3(log n)^2/3) operations using bestclassical
algorithm.
• Shor’salgorithm can accomplish this sametask using
O(n^2(log n(log log n)) operations.
• i.e. aquantum computer canfactor anumber in
exponentially faster than the best knownclassical
algorithm.
13

14. Shor’sAlgorithm
▪Shor’s algorithm shows (in principle,) that a quantum
computer is capable of factoring very large numbers in
polynomial time.
Thealgorithm is dependant on
▪Modular Arithmetic
▪Quantum Parallelism
▪Quantum Fourier Transform

15. 15
Thealgorithm
• Theproblem is: given an odd composite numberN,
find and integer d, strictly between 1 and N, that
divides N.
• TheShor’salgorithm consists of two parts:-
1. Conversion of the problem of factoring to the
problem of finding the period.
2. Finding the period (Quantum period finding) using
the quantum Fourier transform, and is responsible
for quantumspeedup.

16. Classicalpart
1. Arandom number a<Npicked.
2. Compute gcd(a, N). Thismaybe done using the Euclidean
algorithm.
3. Ifgcd(a,N)≠1, then there is anontrivial factor of N.
4. f(x +r) =ax+r mod N=axmod N=f(x).
5. If ris odd, go to step 1.
6. If ar/2 -1 (mod N), go back to step1.
7. gcd(ar/2 ± 1, N) is anon trivial factor of N.
16

17. Shor’s Algorithm - Periodicity
▪ ChooseN=15 and x =7 and we get the following:
3
70mod 15=1
71mod 15=7
72mod 15=4
7 mod 15=13
4
7 mod.15=1
.
.
▪ An important result from NumberTheory:
F(a)=x mod N is aperiodic function
a

18. Shor’s Algorithm - In DepthAnalysis
T
oFactoranodd integerN (Let’schooseN=15) :
1. Choosean integer q suchthat N2
< q <2N2
let’s pick 256
2. Choosearandom integer x such that GCD(x,N) =1 let’s pick 7
3. Create two quantum registers (these registers must alsobe
entangled sothat the collapse of the input register
corresponds to the collapse of the output register)
• Input register: must contain enough qubits to represent
numbers aslarge asq-1. up to 255,so we need 8qubits
• Output register: must contain enough qubits torepresent
numbers aslarge asN-1. up to 14,so we need 4qubits

19. Shor’s Algorithm - PreparingData
4. Loadthe input register with an equally weighted
superposition of all integers from 0to q-1. 0to255
5. Loadthe output register withall zeros.
Thetotal stateof the systemat this point will be:
1
√256 a=0
255
∑|a, 000>
Input
R
egister
Output
R
egister
Note: the comma here
denotes that theregisters
are entangled

20. Shor’s Algorithm - Modular Arithmetic
6. Apply the transformation xa mod Nto each number in the
input register, storing the result of each computation in the
output register.
Input Register 7a Mod 15 Output Register
|0> 70 Mod 15 1
|1> 71 Mod 15 7
|2> 7
2
Mod 15 4
|3> 73 Mod 15 13
|4> 74 Mod 15 1
|5> 75 Mod 15 7
|6> 76 Mod 15 4
|7> 77 Mod 15 13
.
.

21. Shor’s Algorithm -Superposition
Collapse
7. Now take ameasurement on the output register. Thiswill
collapse the superposition to represent just one ofthe
results of thetransformation, let’s call this value c.
Our output register will collapse to represent one of the
following:
|1>,|4>,|7>,or |13>
For sakeof example, lets choose|1>

22. Shor’s Algorithm - Entanglement
8. Sincethe two registers are entangled, measuring the
output register will have the effect of partially collapsing
the input register into an equal superposition of each
state between 0 and q-1 that yielded c (the value of the
collapsed output register.)
Sincethe output register collapsed to |1>, the input register will partially collapse to:
|0>+ |4>+ |8>+ |12>,...
of64 values(0, 4, 8, . . . 252)
1
√64
1 1 1
√64 √64 √64
The probabilities in this caseare 1sinceour register is now in an equalsuperposition
64

23. Shor’s Algorithm - QFT
Wenow apply the Quantum Fourier transform on the
partially collapsed input register. TheFourier transform
hasthe effect of taking astate |a> and transformingit
into astate givenby: 1
√q
q-1
∑|c> *e
c=0
2iac / q
1
√256
255
∑|c> *e
c=0
2iac / 256
1
√64
∑|a> ,|1>
a  A
Note: Ais the set of all valuesthat 7a mod 15 yielded 1. In our caseA={0,
4, 8, …,252}
Sothe final state of the input register after theQFTis:
, |1>
∑
a A
1
√256
∑|c> *e
c=0
1 255
√64
2iac / 256

24. Shor’s Algorithm - QFT
TheQFTwill essentially peak the probability amplitudes at
integer multiples of q/4 in our case 256/4, or 64.
|0>, |64>, |128>, |192>,…
Sowe no longer havean equal superposition of states,the
probability amplitudes of the above states are now higher
than the other states inour register. Wemeasure the
register, and it will collapse with high probability to one of
these multiples of 64, let’s call thisvalue p.
With our knowledge of q, and p, there are methods of
calculating the period (one method is the continuous
fraction expansionof the ratio between q and p.)

25. Shor’s Algorithm - TheFactors
10. Now that we have the period, the factors of N can be
determined by taking the greatest common divisor of
Nwith respect to x ^ (P/2) + 1and
x ^ (P/2) - 1. Theidea here is that this computation
will be done on aclassicalcomputer.
Wecompute:
4/2
Gcd(7 +1, 15) = 5
Gcd(7 4/2
- 1, 15) =3
Successfully factored 15!

26. Shor’s Algorithm -Problems
▪TheQFTcomesup short and revealsthe wrong period.
Thisprobability is actually dependant on your choice of q.
Thelarger the q, the higher the probability of finding the
correct probability.
▪ Theperiod of the series ends up beingodd.
▪Quantum modular exponentiation, much slower thanthe
quantum Fourier transform.
If either of these casesoccur,we goback tothe
beginning and pick anew x.

27. 27
Applications
• Factoring – RSAencryption.
• Quantum simulation.
• Spin-off technology – spintronics, quantum cryptography.
• Spin-off theory – complexity theory, DMRGtheory,N-
represent ability theory.

28. 28
Recentworks on Shor’salgorithm
• In 2001, a7 qubit machine wasbuilt and programmed to
run Shor’salgorithm tosuccessfully factor 15, but no
entanglement isobserved.
• In 2012, the factorization of 21wasachieved.
• In April 2012, the factorization of143 wasachieved
• In April 2016 the 18-bit number 200099 was factored
using quantum annealing on a D-Wave 2X quantum
processor..
• Shortly after, 291311 was factored using NMR.

29. 29
Reference:
• Peter W.Shor“Polynomial-TimeAlgorithms for Prime Factorization
and DiscreteLogarithms on aQuantum Computer “, SIAMJournal
on Computing (1997).
• Michael A. Nielsen & IsaacChuang,‘Quantum computationand
quantum information’, Cambridgeuniversity press.
• Quantum Computing Explained - D.McMahon , (Wiley, 2007).
• An introduction to Quantum Computing - Oxford UniversityPress,
Jan,2007.
• www.eecis.udel.edu/~saunders/courses/879-03s/
• http://www.cs.berkeley.edu/~vazirani/

30. 30
Thankyou