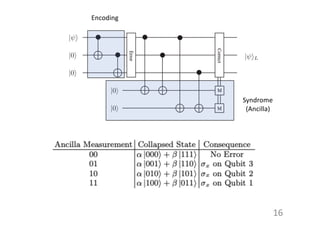
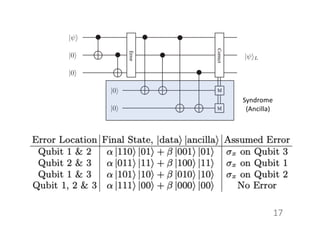
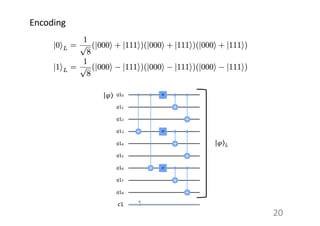
This document provides an introduction to quantum error correction. It discusses the types of quantum errors including coherent errors and environmental decoherence. It then describes the 3-qubit error correction code, which can correct one bit flip error by using syndrome measurements. Finally, it covers the 9-qubit code developed by Shor, which can correct both one bit flip and one phase flip error by combining 3-qubit codes and independently correcting for bit flip and phase flip errors.

1. Quantum Error Correction
for Beginners
section 1-9
2020/04/17 WebEx
National Institute of Informatics
Shin Nishio

2. Paper
[1] Simon J. Devitt, Kae Nemoto, William J. Munro
Quantum Error Correction for Beginners
(Submitted on 18 May 2009, last revised 21 Jun 2013 (this version, v4))
arXiv[quant-ph] 0905.2794
Hands-on: implementation based on [1], written in Qiskit by Shin
https://github.com/parton-quark/QEC-for-Beginners
Abstract
QEC and fault-tolerant quantum computation
• Theoretical aspect of QIS
• Significant development since 1995
• An introduction for researchers other than QEC
2

3. Paper
3
Xavier
Shin (1)
Shin (2)

4. 1. Introduction
4
Research
• Proposal of QEC
• concept of fault-tolerance
• Threshold theorem
• Protocols
• continuous, ion-traps, adiabatic…
• subsystem code, topological code
• Quantum Error Suppression: partially cancel
errors

5. 2. Preliminaries
5
• all operator is Unitary(Excluding measurement)
𝑈𝑈!
= 𝐼
†: Hermitian transpose
• No-cloning theorem
There is no unitary to replicate unknown quantum states.
∄𝑈, 𝑈(| ⟩ψ ⨂ ⟩0 = 𝑈(| ⟩ψ ⨂| ⟩ψ )

6. 3. Quantum Errors
6
Simple Algorithm
1. 𝑁 identity ops
| ⟩𝜑 !"#$%
= '
&
'
𝐼&| ⟩0 = | ⟩0
ideal result

7. 7
2. Three gate(Cancellation)
| ⟩φ !"#$%
= 𝐻𝐼𝐻| ⟩0 = 𝐻𝐼
(
)
, ⟩0 + | ⟩1 = 𝐻
(
)
, ⟩0 + | ⟩1 = | ⟩0
ideal result

8. 8
Errors
A. Coherent quantum errors
B. Environmental decoherence
C. loss, leakage measurement and initialization

9. 9
A. Coherent quantum errors
B. Environmental decoherence
C. loss, leakage measurement and initialization
e.g. Rotation around the X-axis
| ⟩φ !"#$% = %
&
'
𝑒&∈)*| ⟩0 = cos(𝑁𝜖) | ⟩0 + 𝑖 sin(𝑁𝜖) | ⟩1
Undesired gate op

10. 10
A. Coherent quantum errors
B. Environmental decoherence
C. loss, leakage measurement and initialization
e.g. Rotation around the X-axis
| ⟩φ !"#$% = %
&
'
𝑒&∈)*| ⟩0 = cos(𝑁𝜖) | ⟩0 + 𝑖 sin(𝑁𝜖) | ⟩1
Undesired gate op
Probability
𝑃 | ⟩0 = cos!
(𝑁𝜖) ≈ 1 − 𝑁𝜖 !
𝑃 | ⟩1 = sin!
(𝑁𝜖) ≈ 𝑁𝜖 !
𝑃"##$# ≈ 𝑁𝜖 !

11. 11
A. Coherent quantum errors
B. Environmental decoherence
C. loss, leakage measurement and initialization
Assumption (For simplicity)
• two level quantum system ! ⟩𝑒4 , | ⟩𝑒5
• Environment is initialized in the state | ⟩𝐸 = | ⟩𝑒4
• Environment couples to the qubit during the wait
• controlled flip when | ⟩1
• nothing when | ⟩0
Second algorithm

12. 12
A. Coherent quantum errors
B. Environmental decoherence
C. loss, leakage measurement and initialization
Second algorithm
𝐻𝐼𝐻| ⟩0 | ⟩𝐸 =
1
2
! ⟩0 + | ⟩1 | ⟩𝑒4 +
1
2
(! ⟩0 − | ⟩1 )| ⟩𝑒5
Error
measurement result
𝑇𝑟6 𝜌7 =
1
4
⟩|0 ⟨ |0 + ⟩|0 ⟨ |1 + ⟩|1 ⟨ |0 + ⟩|1 ⟨ |1
=
1
2
( ⟩|0 ⟨ |0 + ⟩|1 ⟨ |1 )
+
1
4
⟩|0 ⟨ |0 − ⟩|0 ⟨ |1 − ⟩|1 ⟨ |0 + ⟩|1 ⟨ |1
←classical mixture

13. 13
A. Coherent quantum errors
B. Environmental decoherence
C. loss, leakage measurement and initialization
Measurement Error
1. Positive Operator Value Measures(POVM’s)
𝐹* = 1 − 𝑝+ ⟩|0 ⟨ |0 + 𝑝+ ⟩|1 ⟨ |1
𝐹( = 1 − 𝑝+ ⟩|1 ⟨ |1 + 𝑝+ ⟩|0 ⟨ |0
2. Mapping
𝜌 → 𝜌,
= 1 − 𝑝+ 𝜌 + 𝑝+ 𝑋𝜌𝑋
Leakage
𝑈 ⟩|0 = 𝛼 ⟩|0 + 𝛽 ⟩|1 + 𝛾 ⟩|2

14. 14
A. Coherent quantum errors
B. Environmental decoherence
C. loss, leakage measurement and initialization
Qubit loss: tracing out
𝑇𝑟&(𝜌)
where 𝑖 is the index of the lost qubit
Initialization
• incoherent: initial state
𝜌& = 1 − 𝑝- ⟩|0 ⟨ |0 + 𝑝- ⟩|1 ⟨ |1
where 𝑝- is the probability of initialization
• coherent
⟩| 𝜑 = 𝛼 ⟩|0 + 𝛽 ⟩|1
where 𝑎 ) + 𝛽 ) = 1 and 𝛽 ) ≪ 1

15. 4. The three-qubit code
15
⟩| 𝜑
⟩|0
⟩|0
3-qubit code
• does not represent full quantum code
• cannot simultaneously correct for both
bit and phase flips
• encodes a single logical qubit into three
physical qubits
• # of errors that can be corrected: t
𝑡 =
𝑑 − 1
2

16. 16
Syndrome
(Ancilla)
Encoding

17. 17
Syndrome
(Ancilla)

18. 18
• no error correction scheme will, in general, fully restore
a corrupted state to the original logical state.
• The 3-qubit code can correct one bit-flip error
• others are relaxing these assumptions

19. 5. The nine-qubit code
19
9-qubit code by Shor
• uses 3-qubit code
• can correct
• 1 bit-flip & 1 phase-flip
• one of each
→sufficient to correct for an arbitrary single qubit error
} on one of the nine qubits
• bit-flip and phase-flip on the same qubit
→ Independently corrected

20. 20
Encoding
⟩| 𝜑
⟩| 𝜑 +

21. 21
Correction
• X errors(for each 3-qubit block): same as 3-qubit code
• Z errors
1. Change the basis
1st block
2nd block
3rd block
4. Change the basis
2. Check the parity(1st & 2nd ) 3. Check the parity(2nd & 3rd )

22. 22
Conclusion
• Quantum Errors
• coherent, environmental decoherence, loss, and so on
• the 3-qubit code
• only for bit-flip, uses syndrome
• the 9-qubit code
• combination of Z-error correction & X-error correction