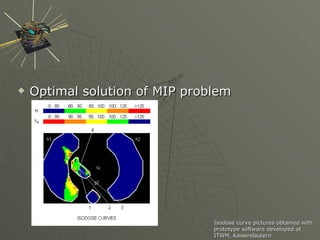
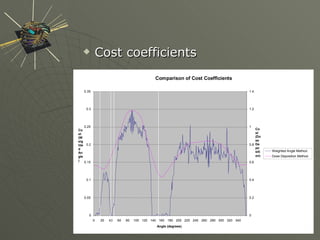
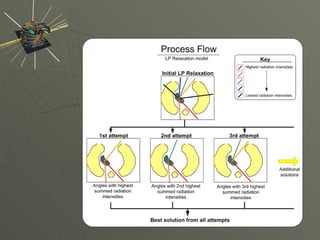
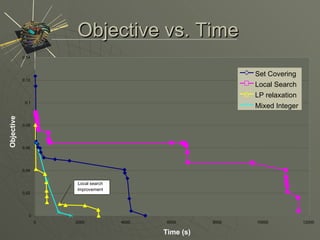
This document summarizes and compares different methods for optimizing irradiation directions in intensity-modulated radiation therapy (IMRT) planning. It formulates the problem as a mixed integer program and evaluates several solution methods including set covering, linear programming relaxation, local search, and a full mixed integer programming approach. Computational results show that all methods can generate good treatment plans within 10 minutes and that optimizing angles is important when few beams are used.

1. Optimisation of Irradiation Directions in IMRT Planning Rick Johnston Matthias Ehrgott Department of Engineering Science University of Auckland M. Ehrgott, R. Johnston Optimisation of Irradiation Directions in IMRT Planning, OR Spectrum 25(2):251-264, 2003

2. What is Radiotherapy?

3. Intensity modulation - improves treatment quality Inverse planning problem - conflicting objectives to irradiate tumour without damage to healthy organs IMRT

4. Model Formulation Discretisation of Body and Beam Voxels Bixels gantry

5. Angle Discretisation Linearises the problem A number of LPs to be solved Replicates physical setup

6. MOMIP Model Data L 1 = lower bound in tumour U k = upper bound in organ k R = number of directions to be used Variables and functions Intensity vector x = (x 11 ,...,x HN ) Direction choice vector y = (y 1 ,...,y H ) Deviation vector T = (T 1 ,...,T K ) Dose distribution vectors D k = (D k1 ,...,D kMk )

7. min (T 1 ,...,T K ) D 1 = P 1 x  (L 1 - T 1 ) 1 D k = P k x  (U k + T k ) 1 , k=2,...,K x hi  My h , h=1,…,H, i=1,…,N y 1 + ...+y H  R y h  {0,1} h=1,...,H T, x  0 To study effect of direction optimisation consider weighted sum min  1 T 1 +  2 T 2 + ... +  K T K Extension of multicriteria model by Hamacher/Küfer

8. Solution Methods Two-phase Methods 3. Set Covering 4. LP Relaxation Integrated Methods 1. Mixed Integer Formulation 2. Local Search Heuristics

9. Integrated Methods CPLEX 7.0 If R increases problem becomes easier, objective value improves For small R and small angle discretisation often no feasible solution found MIP SOLVER 1

10. Optimal solution of MIP problem Isodose curve pictures obtained with prototype software developed at ITWM, Kaiserslautern

11. Integrated Methods Alter each gantry position in turn to find better angles Steepest descent with randomised starting angles Solve LP for each selection of angles LOCAL SEARCH 2

12. Local Search Movie

13. Two-phase Methods Intuitive Considers all angles Relatively quick Fully irradiate every voxel in the tumour Avoid damage to healthy organs Benefits: SET COVERING 3

14. min C 1 y 1 +...+ C S y S Ay  1 y  {0,1} a ij =1 if and only if beam j hits voxel i Weighted angle method C j is sum of  k /U k over all organs at risk and voxels in beam j Dose deposition method C j is sum of  k P k (i,j)/U k over all voxels and all organs at risk

15. Cost coefficients

16. Set Covering Solution MIP Solution

17. Two-Phase Methods LP RELAXATION 4 Optimal solution of LP relaxation 10-40 beams used

19. Results All methods were successful in generating good treatment plans in a reasonable timeframe (10 min) Optimal beams were often counterintuitive Angle optimisation is important if few beams to be used

20. Solution with equidistant beams Solution with optimised beams

21. Comparison Objective 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 Problem 1 3 heads Problem 1 4 heads Problem 2 3 heads Problem 2 4 heads Problem 3 3 heads Set Covering LP relaxation Local Search Mixed Integer

22. Objective vs. Time Objective 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0 2000 4000 6000 8000 10000 12000 Time (s) Local search improvement Set Covering Local Search LP relaxation Mixed Integer