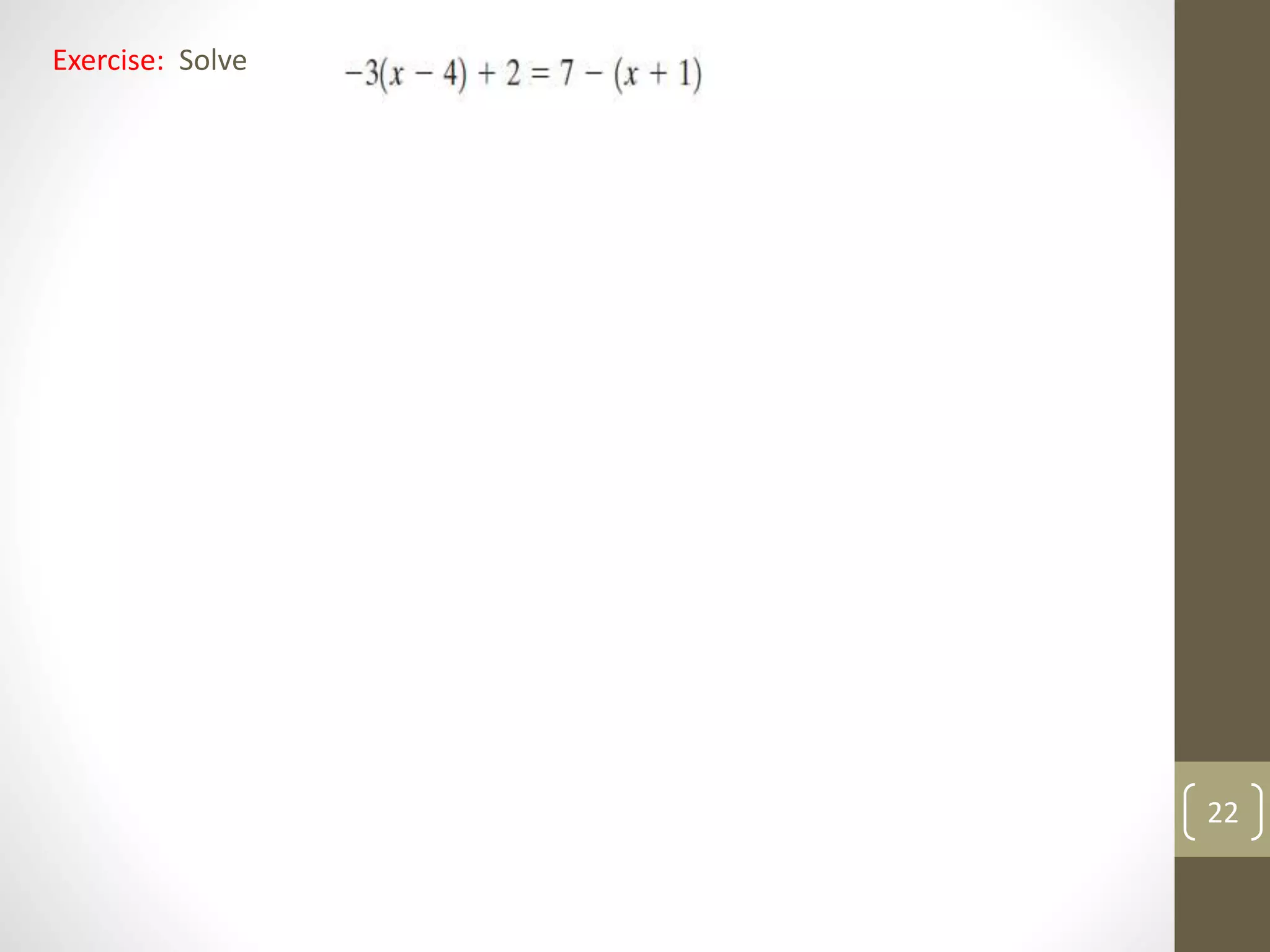This document summarizes key concepts from Chapter 3 of a math textbook, including: - How to solve linear equations in one variable using properties of equality like combining like terms and adding/subtracting the same quantity from both sides. - Examples of solving linear equations by performing inverse operations like subtraction and division. - Determining whether equations are linear based on the highest power of the variable, and providing examples of nonlinear equations. - Checking solutions by showing that both sides of the original equation are equal when the solution is substituted.

1. Chapter 3
Linear Equations, Inequalities,
Quadratic Equations, and Applications
MATH 020
Dr. Farhana Shaheen
1

2. Chapter3
Linear Equations, Inequalities,
Quadratic Equations, and
Applications
• 3.1 Linear Equations in One Variable
• 3.2 Applications of Linear Equations
• 3.3 Linear Inequalities in One Variable
• 3.4 Quadratic Equations
2

3. 3.1
3

4. 3.1 – Linear Equations in One Variable
Solve linear equations involving
fractions
Application of Linear Equations
Objective – Solve linear equations using properties of equality.
-Solve linear equations that can be simplified by combining like terms.
4

5. A. Linear Equations
5

6. 3.1 Linear Equations
Example 1: x + 4 = -2
Example 2: 2x + 5 = 10
Example 3: 5 - 3x = 8
Note: A linear equation is also called a first degree equation since the
highest power of x is 1.
6

7. Determinewither the followingequations are
linear equations in one variable:
1. 10y + 6 = 26
2. 2x + 3y = 11
3. (x  1)2 = 8
4. x is in radical
5. 75
3
2
 x
x
Two variables
x is squared
variable in the denominator
√
7
3x

8. Equivalent equations
Equivalent equations are equations that
have the same solution set:
• Example 2:
5x +2 = 17, 5x =15 and x =3 are
equivalent.
The solution set is {3}.
8

9. Example:
Solve each equations and check your solution:
• 𝒙 + 𝟑 = 𝟐
𝑥 + 3 − 3 = 2 − 3 *subtract 3 from each side of the equation
𝑥 = −1
Check the solution:
L.H.S = −1 + 3 = 2= R.H.S
So the solution is −1.
9

10. •
Example:2 Solve x – 5 = 3
Solution:
10

11. • 2𝑥 + 7 = 𝑥 − 3 *subtract x from each side of
2𝑥 + 7 − 𝑥 = 𝑥 − 3 − 𝑥 the equation
𝑥 + 7 = −3 *subtract 7 from each side of
𝑥 + 7 − 7 = −3 − 7 the equation
𝑥 = −10
Check the solution:
L.H.S= 2 −10 + 7 = −20 + 7 = −13
R.H.S= −10 − 3 = −13
Thus, the solution is −10.
Example:3 Solve 2x + 7 = x - 3
Solution:
11

12. • Example:
• Solve each equation and check your solution:
• 𝟐𝒙 = 𝟔
2𝑥
2
=
6
2
*Divide each side of the equation by 2
𝑥 = 3
12

13. •
Example:4
13

14. Solving Linear Equations
14

15. 15

16. 16

17. Example: Solve , and check your solution
Check the solution:
L.H.S =
R.H.S=
So the solution is
17

18. 18

19. 19

20. Example: Solve 3(x + 5) + 4 = 1 – 2(x + 6), and check your solution.
3(x + 5) + 4 = 1 – 2(x + 6)
3x + 15 + 4 = 1 – 2x – 12
3x + 19 = –2x – 11
3x +19 –19 = –2x – 11 –19
3x = –2x– 30
5𝑥
5
=
−30
5
The solution is 6.
Original equation
Simplify.
Simplify.
Subtract 19.
Add 2x.
Divide by 5.5x = –30
3x+ 2x = –2x+ 2x – 30
x = 6
20

21. Check the solution:
L.H.S = 3(–6 + 5) + 4
= 3(–1) + 4
= 3 + 4
=1
R.H.S= 1 – 2(– 6 + 6)
=1 – 2(0)
=1
So,–6 is a solution of 3(x + 5) + 4 = 1 – 2(x + 6).
21

22. Exercise: Solve
22

23. 23

24. 24

25. 25