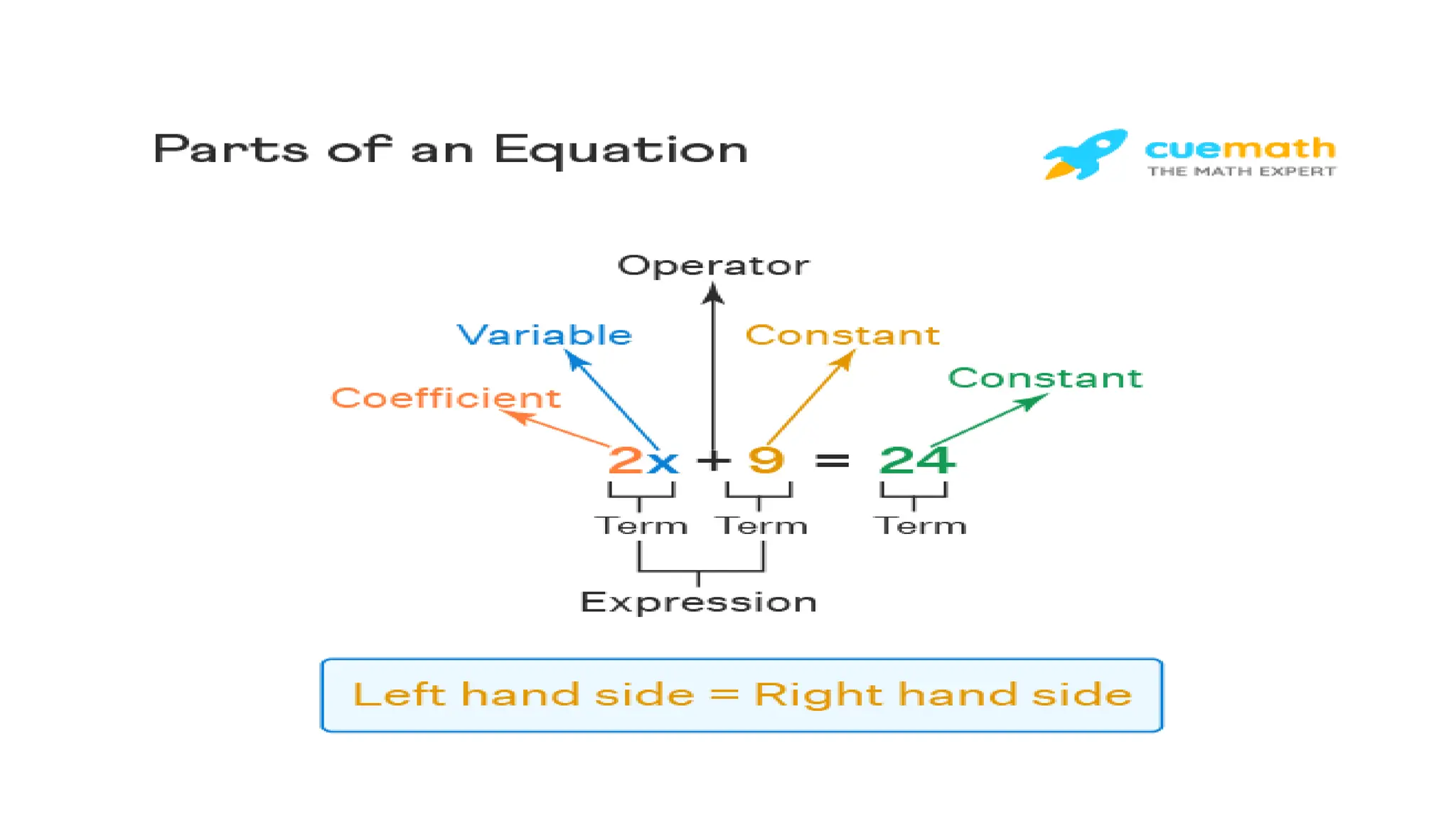
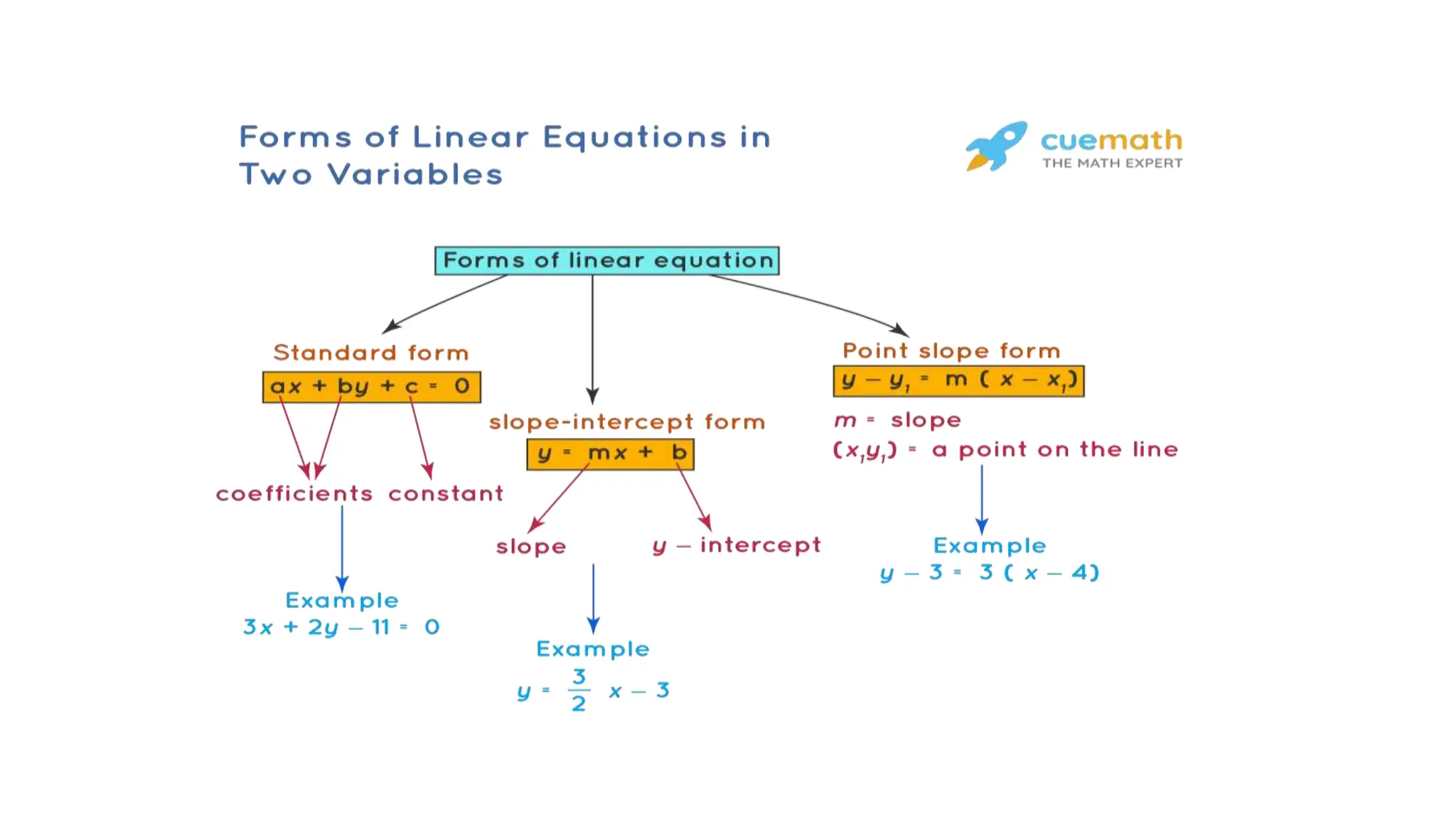
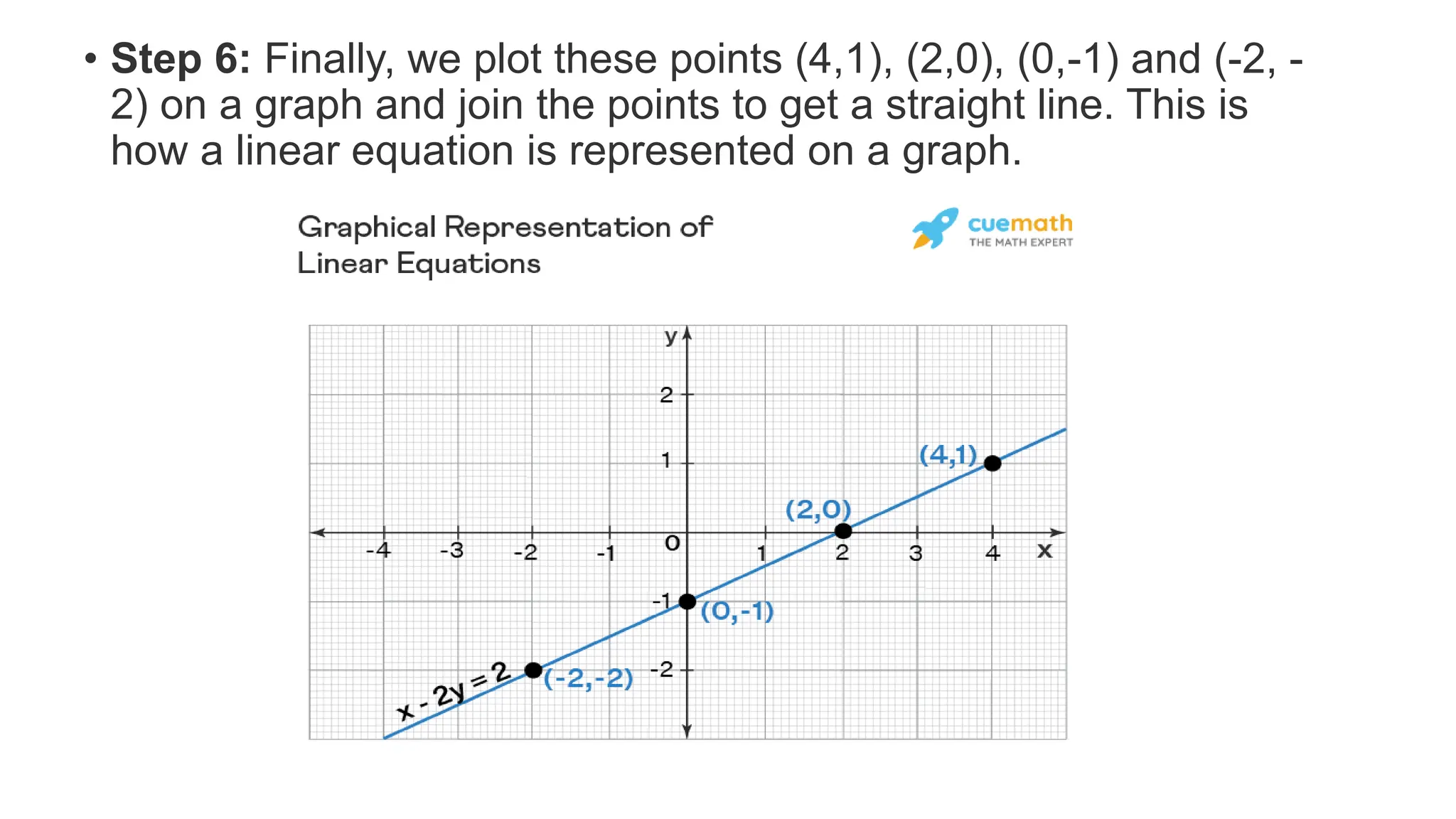
This document discusses equations and expressions. It defines equations as mathematical statements containing two algebraic expressions separated by an equal sign. Equations can be solved to find the value of an unknown variable. The document also discusses the different parts of an equation, how to solve equations by performing the same operations to both sides, and types of equations such as linear, quadratic and cubic equations. It provides examples of solving linear equations in one and two variables.

1. Equation and Expression
Lecture 5

2. What are Equations?
• Equations are mathematical statements containing
two algebraic expressions on both sides of an 'equal to (=)'
sign. It shows the relationship of equality between the
expression written on the left side with the expression written
on the right side.
• In every equation in math, we have, L.H.S = R.H.S (left hand
side = right hand side). Equations can be solved to find the
value of an unknown variable representing an unknown
quantity. If there is no 'equal to' symbol in the statement, it
means it is not an equation

3. • Look at the following examples. These will give you an idea of
the meaning of an equation in math.
Equations
Is it an equation?
1. y = 8x - 9 Yes
2. y + x2 - 7
No, because there is no
'equal to' symbol.
3. 7 + 2 = 10 - 1 Yes

4. Parts of an Equation
• There are different parts of an equation which include coefficients,
variables, operators, constants, terms, expressions, and an equal
to sign.
• When we write an equation, it is mandatory to have an "=" sign, and
terms on both sides. Both sides should be equal to each other.
• An equation doesn't need to have multiple terms on either of the sides,
having variables, and operators.
• An equation can be formed without these as well, for example, 5 + 10
= 15. This is an arithmetic equation with no variables.

6. • Expression: groups of terms connected by addition and
subtraction.

7. How to Solve an Equation?
• An equation is like a weighing balance with equal weights on both
sides. If we add or subtract the same number from both sides of an
equation, it still holds.
• Similarly, if we multiply or divide the same number into both sides of
an equation, it still holds. Consider the equation of a line, 3x − 2 = 4.
We will perform mathematical operations on the LHS and the RHS
so that the balance is not disturbed.
• Let's add 2 on both sides to reduce the LHS to 3x. This will not
disturb the balance. The new LHS is 3x − 2 + 2 = 3x and the new
RHS is 4 + 2 = 6.
• So, the equation becomes 3x = 6. Now, let's divide both sides by 3 to
reduce the LHS to x.
• Thus, the solution of the given equation of a line is x = 2.

8. • Let us take one more example of a basic equation: 3x - 20 = 7.
To bring all the constants on RHS, we have to add 20 to both
sides.
• This implies, 3x - 20 + 20 = 7 + 20, which can be simplified as
3x = 27. Now, divide both sides by 3. This will get you x = 9
which is the required solution of the equation.

9. Types of Equations
Based on the degree, equations can be classified into three
types. Following are the three types of equations in math:
• Linear Equations
• Quadratic Equations
• Cubic Equations

10. Linear Equations
• A linear equation is an equation in which the highest power of
the variable is always 1. It is also known as a one-degree
equation.
• The standard form of a linear equation in one variable is of the
form Ax + B = 0. Here, x is a variable, A is a coefficient and B is
constant.
• The standard form of a linear equation in two variables is of the
form Ax + By = C. Here, x and y are variables, A and B are
coefficients and C is a constant.

11. • An equation that has the highest degree of 1 is known as
a linear equation. This means that no variable in a linear
equation has a variable whose exponent is more than 1. The
graph of a linear equation always forms a straight line.
Equations Linear or Non-Linear
y = 8x - 9 Linear
y = x2 - 7 Non-Linear, the power of the variable x is 2
√y + x = 6 Non-Linear, the power of the variable y is 1/2
y + 3x - 1 = 0 Linear
y2 - x = 9 Non-Linear, the power of the variable y is 2

12. • Example: Solve the linear equation in one variable: 3x + 6 = 18.
• In order to solve the given equation, we bring the numbers on
the right-hand side of the equation and we keep the variable on
the left-hand side. This means, 3x = 18 - 6. Then, as we solve
for x, we get, 3x = 12. Finally, the value of x = 12/3 = 4.

13. Linear Equation in One Variable Questions with
Solutions
1. Convert the given statement into equation: An integer increased
by 5 equals 20.
Solution:
• Given statement: An integer increased by 5 equals 20.
• Assume that the unknown number is “x”.
• Hence, x increased by 5 means x + 5.
• Therefore, the equation x + 5 = 20
• So, an integer increased by 5 equals 20 means x + 5 = 20, which is the
required equation for the given statement.

14. 2. Convert the given equation into a statement: 5x = 25.
Solution:
• The equation given is 5x = 25.
• The statement equivalent to the equation 5x = 25 is “Five times the
number x equals 25”.

15. 3. Find the value of x for the equation 2x – 7 = 21. Also, verify the answer.
Solution:
Given equation: 2x – 7 = 21.
To solve the given equations, keep the variable x on one side and the constants on
the other side.
• Hence, the given equation becomes:
2x = 21 + 7
2x = 28
x = 28/2
x = 14
• Therefore, the value of x is 14.

16. • Verification:
Substitute x = 14 in the equation 2x – 7 = 21
Hence, 2(14) – 7 = 21
28 – 7 = 21
21 = 21
Hence, LHS = RHS.

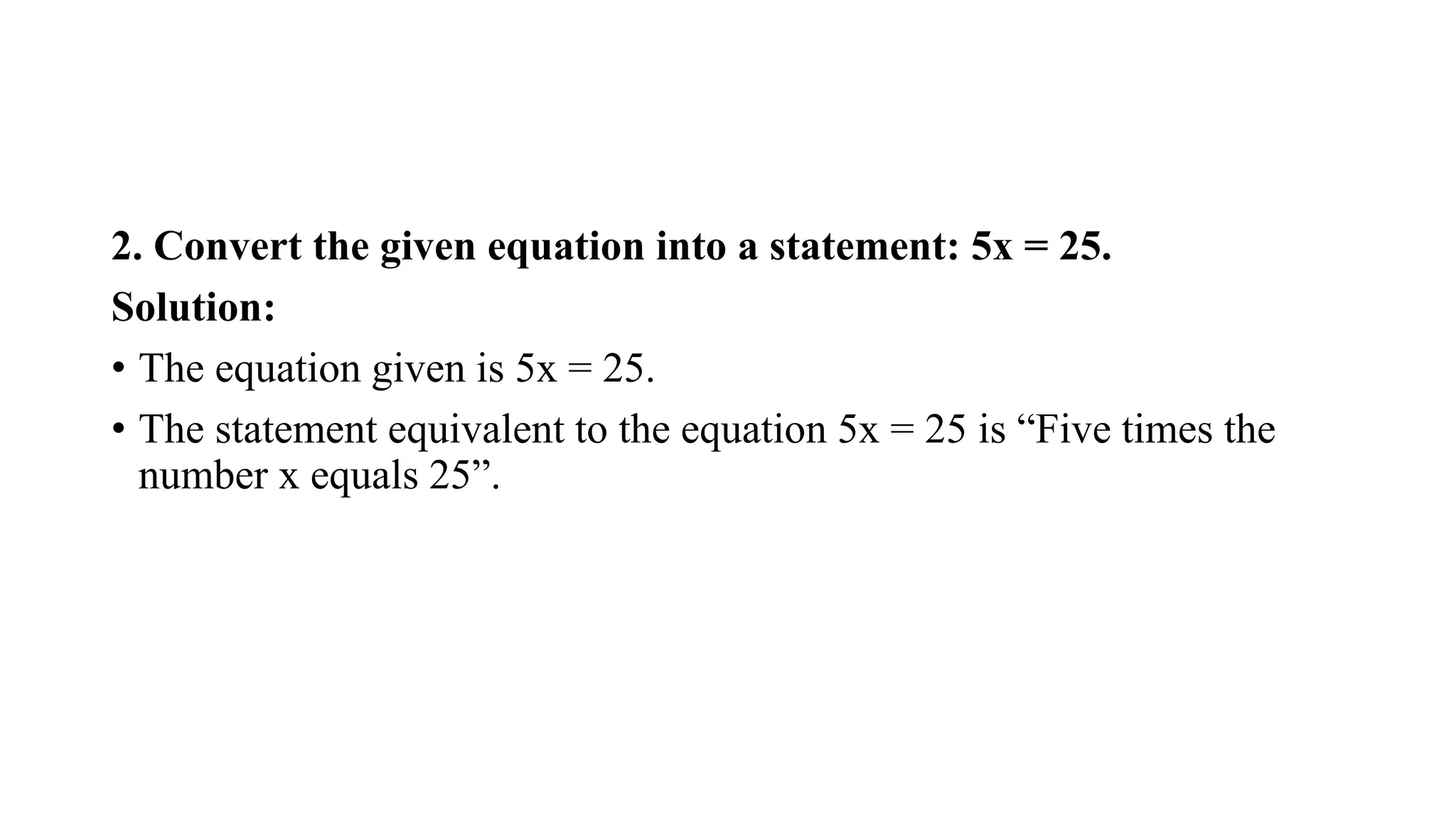
17. 4. Check whether x = 40 is the solution of the equation 5x/2 = 100.
Solution:
To check whether x = 40 is the solution or root of the equation 5x/2 =
100, put the value x = 40 in the equation 5x/2 = 100
⇒ [5(40)]/2 = 100
⇒ 200/2 = 100
⇒ 100 = 100
• Since, LHS = RHS, x = 40 is the solution of the equation 5x/2 = 100

18. Let’s try 
5. Find the number, if 15 is added to three times of the number
results in 45. Also, justify your answer.

19. Solution:
Given statement: 15 is added to three times of the number resulting in 45.
Let the unknown number be x.
Then according to the given statement, the equation formed is:
15 + 3x = 45
Now, keep the variable “x” on one side of the equation and constant on the
other side of the equation.
⇒ 3x = 45 -15
⇒ 3x = 30
⇒ x = 30/3
⇒ x = 10
Therefore, the required number is x = 10.

20. • Verification:
Substitute the value x =10 in the equation 15 + 3x = 45.
⇒ 15 + 3(10) = 45
⇒ 15 + 30 = 45
⇒ 45 = 45
Therefore, LHS = RHS.
Hence, verified.

21. 6. Check whether the given statements are true or false.
1.If x = 5, then 5x – 5 = 20
2.If x = 7, then 4x – 4 = 20.

22. Solution:
(a) Given equation: 5x – 5 = 20
If x = 5,
= 5(5) – 5
= 25 – 5
= 20
Hence, if x = 5, then 5x – 5 = 20.
Therefore, the given equation is true.
(b) Given equation: 4x – 4 = 20
If x = 7,
= 4(7) – 4
= 28 – 4
= 24
Hence, if x = 7, then 4x – 4 = 24.
Therefore, the given equation is
false..

23. Let’s try 
8. Solve the given linear equation: 17 + 6p = 9

24. Given linear equation: 17 + 6p = 9
• Now, keep the variable “p” on the left hand side and bring the constants
on the right hand side.
• Hence, we get
• ⇒ 6p = 9 – 17
• ⇒ 6p = -8
• ⇒ p = -8/6
• ⇒ p = -4/3
• Therefore, the value of p is -4/3.

25. Let’s try 
9. Find the two numbers, if the numbers are in the ratio 5 : 3 and
they differ by 18.

26. • Solution:
Let the unknown number be “p”.
Also, given that, the two numbers are
in the ratio 5 : 3.
According to given conditions, we
can write
⇒ 5p – 3p = 18
⇒ 2p = 18
⇒ p = 18/2
⇒ p = 9.
Therefore, the two numbers are:
• 5p = 5(9) = 45
• 3p = 3(9) = 27
Hence, the required two numbers are
45 and 27.

27. 10. The ages of Rahul and Ramya are in the ratio 5: 7. After 4 years,
the sum of their ages will be 56 years. Find their present ages.

28. Solution:
Assume that the ages of Rahul and Ramya are 5p and 7p.
After 4 years, the ages of Rahul and Ramya will be 5p + 4 and 7p + 4.
According to the given condition, we get the following equation:
(5p + 4) + (7p + 4) = 56
⇒ 12p + 8 = 56
⇒ 12p = 56 – 8
⇒ 12p = 48
⇒ p = 48/12
⇒ p = 4
Therefore, Rahul’s present age = 5(4) = 20
Ramya’s present age = 7(4) = 28.
Hence, the present age of Rahul and Ramya are 20 and 28, respectively.

29. Forms of Linear Equations in Two Variables
A linear equation in two variables can be in different forms like standard
form, intercept form and point-slope form. For example, the same
equation 2x + 3y=9 can be represented in each of the forms like 2x + 3y
- 9=0 (standard form), y = (-2/3)x + 3 (slope-intercept form), and y - 5/3
= -2/3(x + (-2)) (point-slope form). Look at the image given below
showing all these three forms of representing linear equations in two
variables with examples.

31. • Example: Solve the following system of equations using the substitution
method.
x+2y-7=0
2x-5y+13=0
• Solution: Let us solve the equation, x+2y-7=0 for y:
x+2y-7=0
⇒2y=7-x
⇒ y=(7-x)/2
• Substitute this in the equation, 2x-5y+13=0:
• 2x-5y+13=0
⇒ 2x-5((7-x)/2)+13=0
⇒ 2x-(35/2)+(5x/2)+13=0
⇒ 2x + (5x/2) = 35/2 - 13
⇒ 9x/2 = 9/2
⇒ x=1

32. • Substitute x=1 this in the equation y=(7-x)/2:
• y=(7-1)/2 = 3
• Therefore, the solution of the given system is x=1 and y=3.

33. Question: Find the value of variables which satisfies the following equation:
2x + 5y = 20 and 3x+6y =12.
Solution:
• Using the method of substitution to solve the pair of linear equation, we
have:
2x + 5y = 20…………………….(i)
3x+6y =12……………………..(ii)
Multiplying equation (i) by 3 and (ii) by 2, we have:
6x + 15y = 60…………………….(iii)
6x+12y = 24……………………..(iv)

34. Subtracting equation (iv) from (iii)
3y = 36
⇒ y = 12
Substituting the value of y in any of the equation (i) or (ii), we have
2x + 5(12) = 20
⇒ x = −20
Therefore, x=-20 and y =12 is the point where the given equations
intersect.

35. Question 7: The monthly incomes of A and B are in the ratio 8:7 and
their expenditures are in the ratio 19:16. If each saves ₹ 5000 per month,
find the monthly income of each.

36. Solution:
• Let the monthly incomes of A and B be 8x and 7x rupees respectively, and
let their monthly expenditure be 19y and 16y rupees respectively.
• Monthly savings of A = 8x – 19y = 5000 ….(i)
• Monthly savings of B = 7x – 16y = 5000 ….(ii)
• Multiplying (i) 16 and (ii) by 19 and subtracting (ii) from (i) we get
• (16 × 8x – 19 × 7x) = 5000 (16 – 19)
• ⇒ 5x = 15000 ⇒ x = 3000
• Monthly income of A is (8 × 3000) = ₹24,000
• Monthly income of B is (7 × 3000) = ₹21,000

37. Linear Equation Graph
• The graph of a linear equation in one variable x forms a vertical
line that is parallel to the y-axis and vice-versa, whereas, the
graph of a linear equation in two variables x and y forms a
straight line. Let us graph a linear equation in two variables with
the help of the following example.
• Example: Plot a graph for a linear equation in two variables,
x - 2y = 2.

38. • Let us plot the linear equation graph using the following steps.
• Step 1: The given linear equation is x - 2y = 2.
• Step 2: Convert the equation in the form of y = mx + b. This will give: y =
x/2 - 1.
• Step 3: Now, we can replace the value of x for different numbers and get
the resulting value of y to create the coordinates.
• Step 4: When we put x = 0 in the equation, we get y = 0/2 - 1, i.e. y = -1.
Similarly, if we substitute the value of x as 2 in the equation, y = x/2 - 1, we
get y = 0.
• Step 5: If we substitute the value of x as 4, we get y = 1. The value of x = -2
gives the value of y = -2. Now, these pairs of values of (x, y) satisfy the
given linear equation y = x/2 - 1.

39. • Herefore, we list the coordinates as shown in the following
table.
x 0 2 4 -2
y -1 0 1 -2

40. • Step 6: Finally, we plot these points (4,1), (2,0), (0,-1) and (-2, -
2) on a graph and join the points to get a straight line. This is
how a linear equation is represented on a graph.

42. • A quadratic equation is an algebraic equation of the second
degree in x. The quadratic equation in its standard form is ax2 + bx
+ c = 0, where a and b are the coefficients, x is the variable, and c is
the constant term. The important condition for an equation to be a
quadratic equation is the coefficient of x2 is a non-zero term (a ≠ 0).
For writing a quadratic equation in standard form, the x2 term is
written first, followed by the x term, and finally, the constant term is
written.

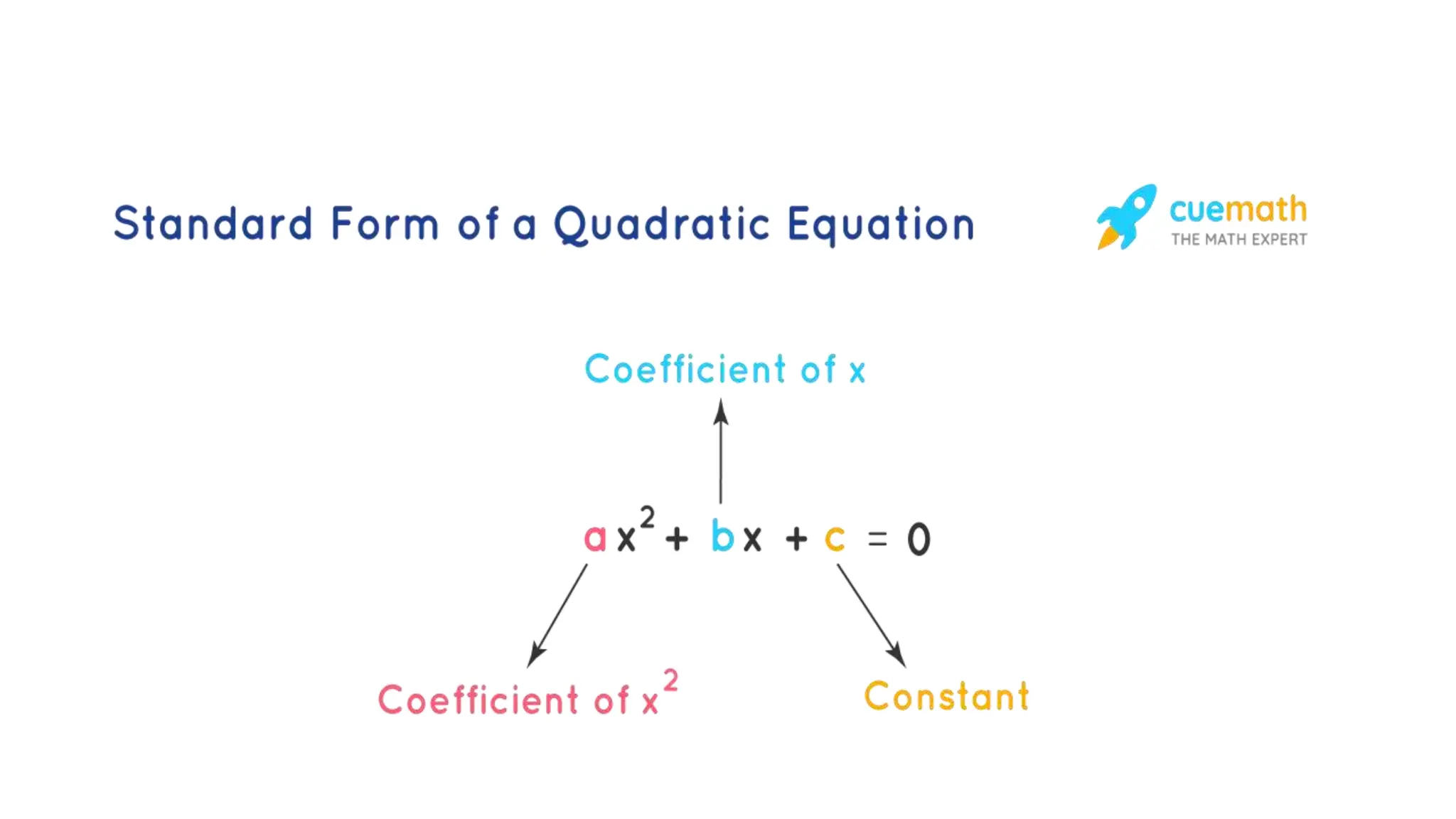
45. Example: Let us find the roots of the same equation that was
mentioned in the earlier section x2 - 3x - 4 = 0 using the quadratic
formula.
• a = 1, b = -3, and c = -4.
• x = [-b ± √(b2 - 4ac)]/2a
= [-(-3) ± √((-3)2 - 4(1)(-4))]/2(1)
= [3 ± √25] / 2
= [3 ± 5] / 2
= (3 + 5)/2 or (3 - 5)/2
= 8/2 or -2/2
= 4 or -1 are the roots.

46. What Is Cubic Equation Formula?
• The cubic equation formula can also be used to derive the curve of a
cubic equation. Representing a cubic equation using a cubic equation
formula is very helpful in finding the roots of the cubic equation.
A polynomial of degree n will have n number of zeros or roots. The
cubic equation is of the following form:
• ax3+bx2+cx+d=0

47. Need to Do More Practice!!