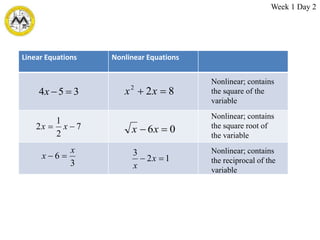
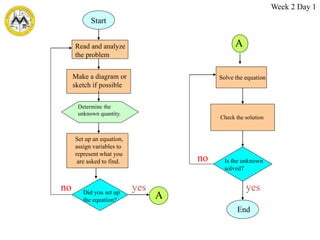
The document provides objectives and lessons for a week 1 algebra course covering linear equations. Key topics covered include classifying and solving different types of linear equations; properties of equality; and solving rational, absolute value, and radical equations. Methods taught for solving linear equations are simplifying expressions, gathering variables to one side, and isolating the variable. Rational equations are solved by determining excluded values, multiplying by the LCD, solving the resulting linear equation, and eliminating extraneous solutions.

1. MATH10
ALGEBRA
LINEAR EQUATIONS
Week 1 Day 1 Linear Equations (Algebra and Trigonometry, Young 2nd Edition, page 90-99)

2. GENERAL OBJECTIVE
• Classify equations as linear, fractional, or rational,
• Solve linear equations,
• Solve equations leading to the form ax+b=0, and
• Solve application problems involving linear equations by
developing mathematical models for real-life problems.
At the end of the lesson the students are expected to:
Week 1 Day 1

3. TODAY’S OBJECTIVE
• Identify an equation,
• Classify equations as identity, conditional or equivalent,
• Distinguish a consistent from an inconsistent equation,
• Enumerate the properties of equality.
At the end of the lesson the students are expected to:
Week 1 Day 1

4. An equation is a statement that two mathematical expressions are
equivalent or equal.
DEFINITION
EQUATION
The values of the unknown that makes the equation true are called
solutions or roots of the equation, and the process of finding the
solution is called solving the equation.
Example:
9
x2

11
7
x 
 x
3
2
x
3
7 


5
x
3
2
x
7
x
4 




1
2
x
x
2
x
3
x





Week 1 Day 1

5. KINDS OF EQUATIONS
• An identity equation is an equation that is true for any number
substituted to the variable.
1
2
1)
(x
.
3
)
3
(
.
3
4
4
3
.
2
2
2










x
x
c
x
x
x
x
b
x
x
a
Example:
Week 1 Day 1

6. • A conditional equation is an equation that is true only for certain
values of the unknown.
1
2)
3(x
.
0
12
4
.
2
3
2
.








x
c
x
b
x
x
a
Example:
Week 1 Day 1

7. • Two equations with exactly the same solutions are called
equivalent equations.
4
.
22
2
5
.
20
5
.




x
c
x
b
x
a
Example:
The following are equivalent equations.
Week 1 Day 1

8. • An inconsistent equation is an equation that has no solution.
• A consistent equation is an equation that has a solution.
Week 1 Day 1

9. EXAMPLE
Determine whether the given equation is an identity or a
conditional equation.
  
 
15
8
5
3
.
5
1
3
1
3
1
.
4
5
3
2
.
3
9
6
4
3
2x
.
2
3
3
9
.
1
2
2
2
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x


















Week 1 Day 1

10. For all real numbers a , b and c
1. Addition Property of Equality
If a = b then a + c = b + c
2. Subtraction Property of Equality
If a = b then a – c = b – c
3. Multiplication Property of Equality
If a = b then a ∙ c = b ∙ c
4. Division Property of Equality
If a =b then
0
c
where
c
b
c
a


PROPERTIES OF EQUALITY
Week 1 Day 1

11. TODAY’S OBJECTIVE
• Define linear equations in one variable,
• Determine the difference between linear and nonlinear
equations,
• Enumerate the steps in solving linear equations,
• Solve linear equations and equations involving fractions,
• Solve rational equations which are reducible to linear
equations,
• Define extraneous solution.
At the end of the lesson the students are expected to:
Week 1 Day 2

12. RECALL
• An identity equation is an equation that is true for any number
substituted to the variable.
• An equation is a statement that two mathematical expressions
are equivalent or equal.
• A conditional equation is an equation that is true only for certain
values of the unknown.
• Two equations with exactly the same solutions are called
equivalent equations.
• An inconsistent equation is an equation that has no solution.
• A consistent equation is an equation that has a solution.
Week 1 Day 2

13. DEFINITION
LINEAR EQUATION IN ONE VARIABLE
A linear equation in one variable is an equation that can
be written in the form
ax + b = 0
where a and b are real numbers and a  0
Example:
2x – 1 = 0, -5x = 10 + x, 3x + 8 = 2
Week 1 Day 2

14. Linear Equations Nonlinear Equations
3
5
4 

x 8
2
2

 x
x
7
2
1
2 
 x
x 0
6 
 x
x
3
6
x
x 
 1
2
3

 x
x
Nonlinear; contains
the square of the
variable
Nonlinear; contains
the reciprocal of the
variable
Nonlinear; contains
the square root of
the variable
Week 1 Day 2

15. SOLVING A LINEAR EQUATION IN ONE VARIABLE
Steps
1. Simplify the algebraic expressions on both sides of the equation.
2. Gather all the variable terms on one side of the equation and
all constant terms on the other side.
3. Isolate the variable.
4. Check the solution by substituting the value of the
unknown into the original equation.
Week 1 Day 2

16. EXAMPLE
STEP DESCRIPTION EXAMPLE
1 Simplify the algebraic expression
on both sides
2(x-1)+3 = x-3(x+1)
2x-2+3 = x-3x-3
2x+1 = -2x-3
2 Gather all the variables on one
side of the equation and all
constant terms on the other side.
2x+2x = -3-1
4x = -4
3 Isolate the variable
1
-
x
4
4
x



Problem #23 on page 97
Week 1 Day 2
Solve for the indicated variable: 2(x-1)+3=x-3(x+1)

17. Solve the following equations.
 
     
 
3
y
3
1
y
5
5
y
2
3
2
y
3
-
5y
2
-
25
97
.
pp
32
#









 
     
 
y
6
4
3
y
2
6
2
7
y
4
7
2
-
6y
9
8y
-
7
-
46
97
.
pp
36
#








Week 1 Day 2

18. Linear Equations Involving Fractions.
4
63
x
2
7
x
97
.
pp
39
#


15
1
x
6
5
2
x
3
5
-
x
-
1
97
.
pp
48
# 



Week 1 Day 2

19. SOLVING RATIONAL EQUATIONS THAT ARE REDUCIBLE
TO LINEAR EQUATIONS
A rational equation is an equation that contains one or more
rational expressions.
Extraneous solution are solutions that satisfy a transformed
equation but do not satisfy the original equation.
Steps
1. Determine any excluded values(denominator equals 0).
2. Multiply the equation by the LCD.
3. Solve the resulting linear equation.
4. Eliminate any extraneous solution.
Week 1 Day 2

20. a
7
12
2
a
2
93
.
pp
1.1.4
ex.
Classroom
.
1 

)
4
a
(
a
8
a
5
4
-
a
2
94
.
pp
1.1.5
ex.
Classroom
.
2



x
3
x
1
6
x
2
1
12
-
4x
1
95
.
pp
1.1.6
ex.
Classroom
.
3 2




3
x
1
5
-
2x
2
95
.
pp
1.1.7
ex.
Classroom
.
4



Solve the following equations.
4
2
1
u
u
u
Edition
2nd
Watson
and
Redlin
,
by Stewart
ry
Trigonomet
&
Algebra
78
page
1.1
exercise
.
5











EXAMPLE Week 1 Day 2

21. TODAY’S OBJECTIVE
• Solve equations using radicals
• Solve absolute value equations
• Solve literal equations
At the end of the lesson the students are expected to:
Week 1 Day 3

22. RECALL
• Steps in solving linear equations
• A rational equation is an equation that contains one or more
rational expressions.
• Steps in solving rational equations.
• Extraneous solution are solutions that satisfy a transformed
equation but do not satisfy the original equation.
Week 1 Day 3

23. SOLVING EQUATIONS USING RADICALS
solution
real
no
has
equation
the
a
and
even
is
n
if
a
and
even
is
n
if
a
odd
is
n
if
a
x
solution
a
has
a
x
equation
The
n
n
n
,
0
0
x






exist
not
does
because
solution
real
no
has
x
x
solution
real
one
only
has
x
x
solutions
real
two
has
x
x
solution
real
one
only
has
x
Examples
16
16
2
32
:
32
2
16
:
16
2
32
:
32
:
4
4
5
5
4
4
5
5

















Week 1 Day 3

24. 12
3
x
2
.
1 

Solve each equations:
Week 1 Day 3
5
1
x
3
.
2 

12
6
x
2
5
.
3 



25. ABSOLUTE VALUE EQUATIONS
DEFINITION The absolute value of a number a is given by
.
line
number
real
the
on
a
and
x
between
ce
tan
dis
the
is
a
x
,
generally
More
.
origin
the
to
a
of
ce
tan
dis
the
represents
it
that
and
0
a
if
a
0
a
if
a
a








Week 1 Day 3

26. Solve each equations: (examples on page 131)
14
5
7
x
3
.
2
3
5
x
2
.
1





Solve each equations:
2
x
3
1
-
x
.
17
15
6
5
x
3
.
13





EXAMPLE
Edition
2nd
Watson
and
Redlin
,
by Stewart
ry
Trigonomet
&
Algebra
131
page
from
Exercise 







Edition
2nd
Watson
and
Redlin
,
by Stewart
ry
Trigonomet
&
Algebra
133
page
from
Exercise 







Week 1 Day 3

27. SOLVING FOR ONE VARIABLE IN TERMS OF THE OTHER
Many formulas in the sciences involve several variables,
and it is often necessary to express one of the variables in
terms of the others.
2
r
r
mM
G
F
equation
the
in
M
iable
va
the
for
solve

lh
wh
lw
A
equation
the
in
w
iable
va
the
for
solve
2
2
2
r



Edition
2nd
Watson
and
Redlin
,
by Stewart
ry
Trigonomet
&
Algebra
72
-
71
page
from
Example 







Week 1 Day 3

28. SUMMARY
• LINEAR EQUATIONS ARE SOLVED BY :
1. Simplifying the algebraic expressions on both sides of the equation.
2. Gathering all the variable terms on one side of the equation and
all constant terms on the other side.
3. Isolating the variable.
4. Checking the solution by substituting the value of the
unknown into the original equation.
• RATIONAL EQUATIONS ARE SOLVED BY :
1. Determining any excluded values(denominator equals 0).
2. Multiplying the equation by the LCD.
3. Solving the resulting linear equation.
4. Eliminating any extraneous solution.
Week 1 Day 3

29. CLASSWORK
HOMEWORK
#s 31,33,35,43,46,51,55,57,61, 65 page 97-98
#s 32, 34, 42, 60 page 97
Week 1 Day 3

30. APPLICATION INVOLVING LINEAR
EQUATIONS
Week 2 Day 1 Application Involving Linear Equations (Algebra and Trigonometry, Young 2nd
Edition, page 100-113).

31. TODAY’S OBJECTIVE
• Develop mathematical models for real-life problems,
• Solve application problems involving common formulas,
• Solve number problems,
• Solve digit problems,
• Solve geometric problems, and
• Solve money and coin problems.
Week 2 Day 1

32. STEPS IN SOLVING WORD PROBLEMS
1. Read and analyze the problem carefully and make sure you
understand it.
2. Make a diagram or sketch, if possible.
3. Determine the unknown quantity. Choose a letter to
represent it.
4. Set up an equation. Assign a variable to represent what you
are asked to find.
5. Solve the equation for the unknown quantity.
6. Check the solution.
Week 2 Day 1

33. Start
Read and analyze
the problem
Make a diagram or
sketch if possible
Determine the
unknown quantity.
Did you set up
the equation?
Set up an equation,
assign variables to
represent what you
are asked to find.
A
no yes
A
Solve the equation
Check the solution
Is the unknown
solved?
no
yes
End
Week 2 Day 1

34. NUMBER PROBLEMS
1. Find three consecutive odd integers so that the sum of the
three integers is 5 less than 4 times the first.
(Example 2 page 102)
2. Find two consecutive even integer s so that 18 times the
smallest number is 2 more than 17 times the larger number.
(Classroom Ex. 1.2.2 page 102)
Week 2 Day 1

35. GEOMETRY PROBLEMS
1. A rectangle 3 inches wide has the same area as a square with
9 inch sides. What are the dimensions of the rectangle?
(Your Turn problem page 103)
2. Consider two circles, a smaller one and a larger one. If the
larger has a radius that is 3 feet larger than that of the smaller
circle and the ratio of the circumferences is 2:1, what are the
radii of the two circles. (#21 page 110)
Week 2 Day 1

36. DIGIT PROBLEMS
1. In an integer between 10 and 100, the unit’s digit is 3 greater
than the ten’s digit. Find the integer, if it is 4 times as large as
the sum of its digits.
(from Internet Guide to Engineering Mathematics)
2. A certain two digit number is equal to 9 times the sum of its
digits. If 63 were subtracted from the number the digits would
be reversed. Find the number.
(from Internet Guide to Engineering Mathematics)
3. The sum of the digits of a two-digit number is 11. If we
interchange the digits then the new number formed is 45 less
than the original. Find the original number.
(onlinemathlearning .com)
Week 2 Day 1

37. MONEY AND COIN PROBLEMS
1. A change purse contains an equal number of pennies, nickels
and dimes. The total value of the coins is $1.44. How many of
each type does the purse contain?
(# 25 page 89 Algebra and Trig. By Stewart, Redlin and Watson, 2nd edition)
2. Mary has $3.00 in nickels, dimes and quarters. If she has twice
as many dimes as quarters and five more nickels than dimes,
how many coins of each type doe she have?
(# 26 page 89 Algebra and Trig. By Stewart, Redlin and Watson, 2nd edition)
Week 2 Day 1

38. TODAY’S OBJECTIVE
• Solve investment problems,
• Solve age problems, and
• Solve mixture problems.
At the end of the lesson the students are expected to:
Week 2 Day 2

39. INVESTMENT PROBLEMS
1. An ambitious 14-year old has saved $1,800 from chores and
odd jobs around the neighborhood. If he puts this money into a
CD that pays a simple interest rate of 4% a year, how much
money will he have in his CD at the end of 18 months?
(Classroom Ex. 1.2.4 page 104)
2. Theresa earns a full athletic scholarship for college, and her
parents have given her the $20,000 they had saved to pay for
her college tuition. She decides to invest that money with an
overall goal of earning 11% interest. She wants to put some the
money in a low-risk investment that has been earning 8% a year
and the rest of the money in a medium-risk investment that
typically earns 12% a year. How much money should she put in
each investment to reach her goal?
(Example #5 page 105)
Week 2 Day 2

40. AGE PROBLEMS
1. A father is four times as old as his daughter. In 6 years, he will
be three times as old as she is now. How old is the daughter
now?
(# 22 page 89 Algebra and Trig. By Stewart, Redlin and Watson, 2nd edition)
2. A movie star, unwilling to give his age, posed the following
riddle to a gossip columnist. “Seven years ago, I was eleven
times as old ad my daughter. Now I am four times as old as
she is.” How old is the star?
(# 23 page 89 Algebra and Trig. By Stewart, Redlin and Watson, 2nd edition)
Week 2 Day 2

41. MIXTURE PROBLEMS
1. A mechanic is working on the coolant system of a vehicle with
a capacity of 11.0 liters. Currently the system is filled with
coolant that is 45% ethylene glycol. How much fluid must be
drained and replaced with 100% ethylene glycol so that the
system will be filled with coolant that is 60% ethylene glycol?
(Classroom Ex. 1.2.6 page 106)
2. For a certain experiment, a student requires 100 ml of a
solution that is 8% HCl(hydrochloric acid). The storeroom has
only solutions that are 5% and 15% HCl. How many milliliters
of each available solution should be mixed to get a 100 ml of
8% HCl?
(# 33 page 111)
Week 2 Day 2

42. MIXTURE PROBLEMS
3. A cylinder contains 50 liters of a 60% chemical solution.
How much of this solution should be drained off and
replaced with a 40% solution to obtain a final strength of
46%?
(#30 page 37 Applied College Algebra and Trig. By Linda Davis 3rd edition)
Week 2 Day 2

43. TODAY’S OBJECTIVE
• Solve uniform motion problems,
• Solve work problems, and
• Solve clock problems.
At the end of the lesson the students are expected to:
Week 2 Day 3

44. UNIFORM MOTION PROBLEMS
1. You and your roommate decided to take a road trip to the
beach one weekend. You drove all the way to the beach at an
average speed of 60 mph. Your roommate drove all ath e way
back (on the same route, but with no traffic) at an average
rate of 75mph. If the total trip drive took a total of 9 hours,
how many miles was the trip to the beach?
(Classroom Ex. 1.2.7 page 108)
2. A Cessna 150 averages 150 mph in still air. With a tailwind it is
able to make a trip in 2 1/3 hours. Because of the headwind, it
is only able to make a return trip in 3 ½ hours. What is the
average wind speed?
(Your turn problem page 108)
Week 2 Day 3

45. UNIFORM MOTION PROBLEMS
3. A motorboat can maintain a constant speed of 16 mph relative
to the water. The boat makes a trip upstream to a marina in 20
minutes. The return trip takes 15 minutes. What is the speed
of the current? (# 41 page 111)
4. On a trip Jerry drove a steady speed for 3 hours. An accident
slowed his speed by 30 mph for the last part of the trip. If the
190-mile trip took 4 hours, what was his speed during the first
part of the trip?
(#37 page 37 Applied College Algebra and Trig. By Linda Davis 3rd edition)
Week 2 Day 3

46. WORK PROBLEMS
1. Connie can clean her house in 2 hours. If Alvaro helps her,
they can clean the house in 1 hour and 15 minutes together.
How long would it take Alvaro to clean the house by himself?
(Example #8 page 109)
2. Next-door neighbors Bob and Jim use hoses from both houses
to fill Bob’s swimming pool. They know it takes 18 hours using
both hoses. They also knew that Bob’s hose, used alone, takes
20% less time that Jim’s hose alone. How much time is
required to fill the pool by each hose alone?
(#48 page 91 Algebra and Trig. By Stewart, Redlin and Watson, 2nd edition)
Week 2 Day 3

47. WORK PROBLEMS
3. It takes 7 people 12 hours to complete a job. If they worked at
the same rate, how many people would it take to complete
the job in 16 hours.
(#22 page 37 Applied College Algebra and Trig. By Linda Davis 3rd edition)
Week 2 Day 3

48. CLOCK PROBLEMS
1. What time after 8 o’ clock will the hands of the continuously
driven clock be opposite each other?
2. What time after 5:00 am will the hands of the continuously
driven clock extend in opposite direction?
3. What time after 3:00 pm will the hands of the continuously
driven clock are together for the first time?
4. What time after 4 o’ clock will the hands of the continuously
driven clock from a right angle?
Week 2 Day 3

49. SUMMARY
In real world many kinds of application problems can be solved
through modeling with linear equations. The following
procedure will help you develop the model. Some problems
require development of a mathematical model, while others rely
on common formulas.
1. Read and analyze the problem carefully and make sure you
understand it.
2. Make a diagram or sketch, if possible.
3. Determine the unknown quantity. Choose a letter to represent
it.
4. Set up an equation. Assign a variable to represent what you are
asked to find.
5. Solve the equation for the unknown quantity.
6. Check the solution.
Week 2 Day 3

50. CLASSWORK
HOMEWORK
#s 15,19,31,34,38,42,44,47,50,73 page 110-113
Classroom example 1.2.6 page 106 and 1.2.7 page 108
Week 2 Day 3