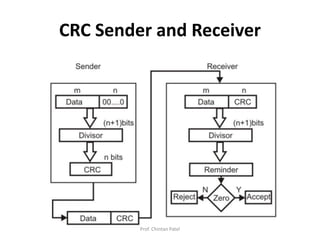
This document discusses Cyclic Redundancy Check (CRC), a technique used to detect errors in digital data during transmission or storage. CRC works by calculating a checksum based on the remainder of binary long division of the transmitted data divided by a fixed, predetermined polynomial. The sender appends the CRC checksum to the end of the message before transmission. The receiver re-calculates the CRC and checks if it matches, to detect any errors introduced during transmission. Examples are provided to demonstrate how CRC encoding and decoding works using different generator polynomials.


![• Procedure at sender side :
1. Determine size of original massage (k bits)
2. Establish Generator Polynomial (r + 1 bits).
3. Append r zeros with original message [x = (k (Message)+ r (zeros))]
4. Divide this x by the generator polynomial.
5. Append remainder(also considered as a FCS of r bits) with original
message k.
6. Transmit this data.
• Procedure at Receiver side :
1. Receive k + r bits
2. Establish Generator Polynomial(r+1 bits)
3. Divide this bits by generator polynomial.
4. If remainder is all bits 0 , no error in transmission
Prof. Chintan Patel](https://image.slidesharecdn.com/crc-140821211949-phpapp01/85/Crc-3-320.jpg)