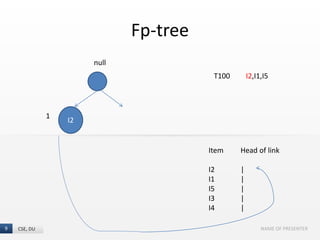
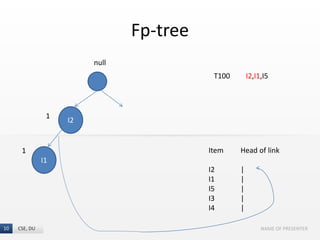
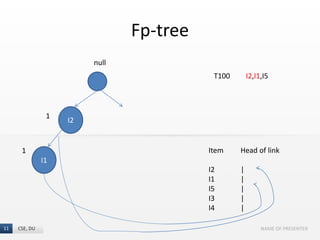
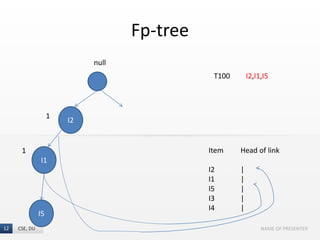
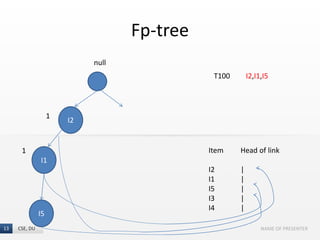
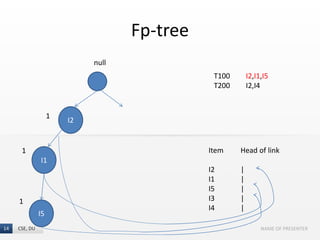
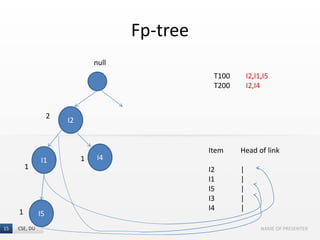
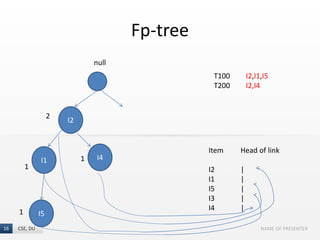
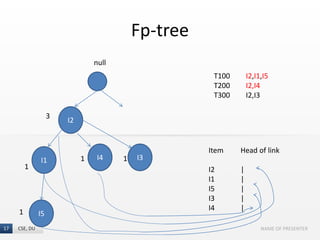
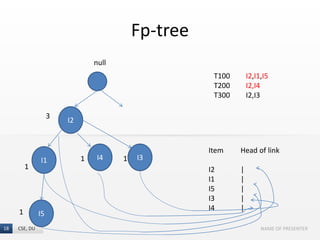
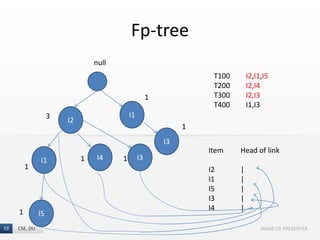
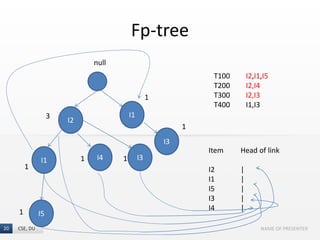
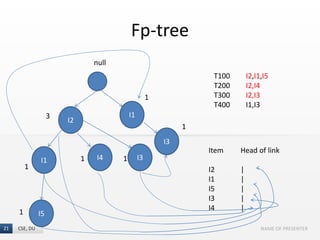
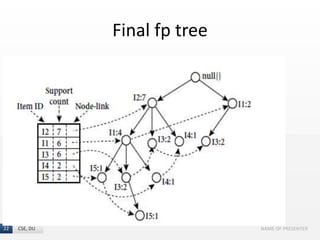
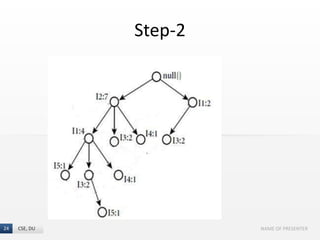
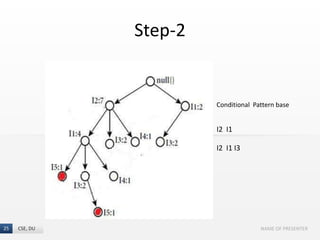
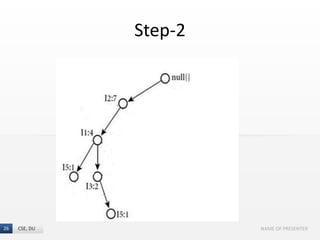
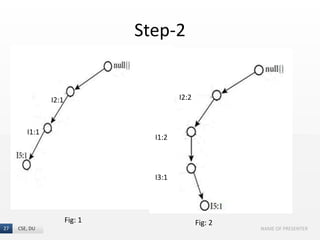
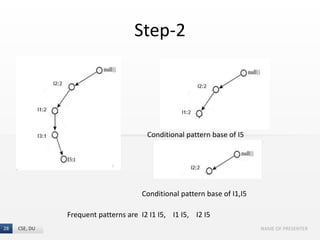
The document presents the FP-Growth algorithm, an efficient method for mining frequent patterns in data without candidate generation, utilizing a divide-and-conquer strategy. It details the FP-tree construction process, including scanning the database and creating conditional FP-trees for mining. The algorithm is noted for its reduced memory usage and efficiency in discovering both long and short frequent patterns.

1. 1 I NAME OF PRESENTER
FP Algorithm
Ashis Kumar Chanda
Department of Computer Science and Engineering
University of Dhaka

2. 2 I NAME OF PRESENTERCSE, DU2
Key concepts
oIntroduction
o Idea of FP
o FP-construction
o Analysis of FP

3. 3 I NAME OF PRESENTERCSE, DU3
Introduction
The First & main algorithm of Data mining is
Apriori
But it has some Bottleneck
Bottleneck: candidate-generation and test
So, a question arise
Can we avoid candidate generation?

4. 4 I NAME OF PRESENTERCSE, DU4
Idea of FP
Frequent pattern growth adopts a divide-and-
conquer strategy
It just scan database two times & use no
candidate set
We define two parts in FP-construction

5. 5 I NAME OF PRESENTERCSE, DU5
FP-construction
Stpe-1:
1. First scan database, find frequent number
of each element
2. Then sort them in descending order
3. Now make a tree with root as null
4. Now scan database secondly, sort
transaction according to descending
support count
T100: I1, I2, I5
T100: I2, I1, I5

6. 6 I NAME OF PRESENTERCSE, DU6
FP-construction
TID List items
T100 I2,I1,I5
T200 I2,I4
T300 I2,I3
T400 I2,I1,I4
---- ---
---- ---

7. 7 I NAME OF PRESENTER
Fp-tree
7
null
T100 I2,I1,I5
CSE, DU

8. 8 I NAME OF PRESENTER
Fp-tree
8
null
T100 I2,I1,I5
I2
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

9. 9 I NAME OF PRESENTER
Fp-tree
9
null
T100 I2,I1,I5
I2
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

10. 10 I NAME OF PRESENTER
Fp-tree
10
null
T100 I2,I1,I5
I2
I1
1
1 Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

11. 11 I NAME OF PRESENTER
Fp-tree
11
null
T100 I2,I1,I5
I2
I1
1
1 Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

12. 12 I NAME OF PRESENTER
Fp-tree
12
null
T100 I2,I1,I5
I2
I1
I5
1
1 Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

13. 13 I NAME OF PRESENTER
Fp-tree
13
null
T100 I2,I1,I5
I2
I1
I5
1
1 Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

14. 14 I NAME OF PRESENTER
Fp-tree
14
null
T100 I2,I1,I5
T200 I2,I4
I2
I1
I5
1
1
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

15. 15 I NAME OF PRESENTER
Fp-tree
15
null
T100 I2,I1,I5
T200 I2,I4
I2
I1
I5
I4
2
1
1
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

16. 16 I NAME OF PRESENTER
Fp-tree
16
null
T100 I2,I1,I5
T200 I2,I4
I2
I1
I5
I4
2
1
1
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

17. 17 I NAME OF PRESENTER
Fp-tree
17
null
T100 I2,I1,I5
T200 I2,I4
T300 I2,I3
I2
I1
I5
I4 I3
3
1
1
1 1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

18. 18 I NAME OF PRESENTER
Fp-tree
18
null
T100 I2,I1,I5
T200 I2,I4
T300 I2,I3
I2
I1
I5
I4 I3
3
1
1
1 1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

19. 19 I NAME OF PRESENTER
Fp-tree
19
null
T100 I2,I1,I5
T200 I2,I4
T300 I2,I3
T400 I1,I3
I2
I1
I5
I4 I3
3
1
1
1 1
I1
1
I3
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

20. 20 I NAME OF PRESENTER
Fp-tree
20
null
T100 I2,I1,I5
T200 I2,I4
T300 I2,I3
T400 I1,I3
I2
I1
I5
I4 I3
3
1
1
1 1
I1
1
I3
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

21. 21 I NAME OF PRESENTER
Fp-tree
21
null
T100 I2,I1,I5
T200 I2,I4
T300 I2,I3
T400 I1,I3
I2
I1
I5
I4 I3
3
1
1
1 1
I1
1
I3
1
Item Head of link
I2 |
I1 |
I5 |
I3 |
I4 |
CSE, DU

22. 22 I NAME OF PRESENTER
Final fp tree
22 CSE, DU

23. 23 I NAME OF PRESENTER
FP-construction
• Step-2:
• Now make conditional FP-tree by perform
mining recursively
• Then perform concatenation of the suffix
pattern
• And we get generated frequent patterns
23 CSE, DU

24. 24 I NAME OF PRESENTER
Step-2
24 CSE, DU

25. 25 I NAME OF PRESENTER
Step-2
25
I2 I1
I2 I1 I3
Conditional Pattern base
CSE, DU

26. 26 I NAME OF PRESENTER
Step-2
26 CSE, DU

27. 27 I NAME OF PRESENTER
Step-2
27
I2:1
I1:1
I2:2
I1:2
I3:1
Fig: 1 Fig: 2
CSE, DU

28. 28 I NAME OF PRESENTER
Step-2
28
dd
Conditional pattern base of I5
Conditional pattern base of I1,I5
Frequent patterns are I2 I1 I5, I1 I5, I2 I5
CSE, DU

29. 29 I NAME OF PRESENTERCSE, DU29
Final Output

30. 30 I NAME OF PRESENTERCSE, DU30
Analysis of FP
 No candidate element
 Scan database only two times
 No need to use huge memory
 Efficient for mining both long & short
frequent patterns

31. 31 I NAME OF PRESENTERCSE, DU31
Complexity
Complexity of searching through all paths
is bounded by
O(header_count2 * depth of tree)
Creation of a new cFP-Tree occurs also

32. 32 I NAME OF PRESENTERCSE, DU32
FP-Tree size
The FP-Tree usually has a smaller size
– Best case scenario:
all transactions contain the same set of items
• 1 path in the FP-tree
– Worst case scenario: every transaction has a unique set of
items (no items in common)
The size of the FP-tree depends on how the items are
ordered
Ordering by decreasing support is typically used but it
does not always lead to the smallest tree (it's a heuristic)

33. 33 I NAME OF PRESENTERCSE, DU33
References
- Data Mining Concepts & Techniques
by J. Han & M. Kamber
- Database system Concept
by Abraham Sillberschatz, Korth, Sudarshan
- Lecture of Dr. S. Srinath
Institute of Technology at Madras, India