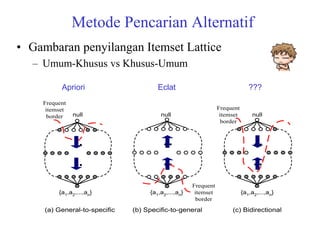
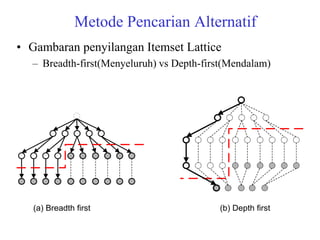
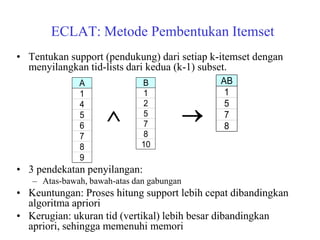
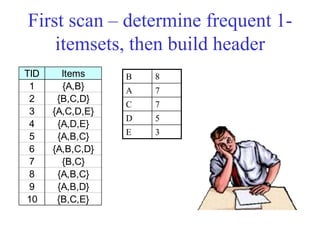
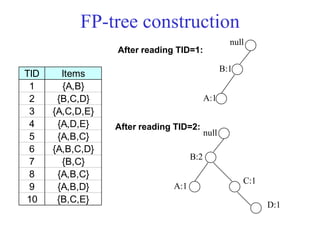
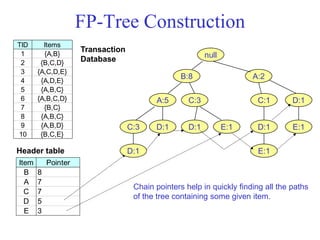
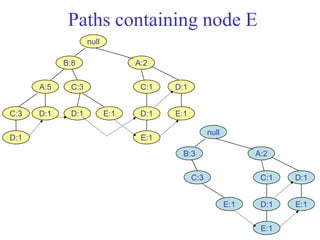
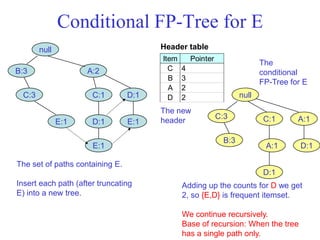
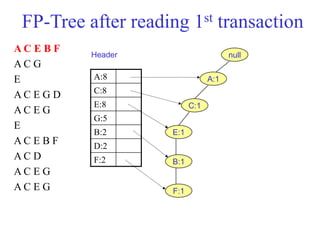
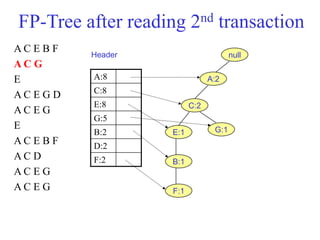
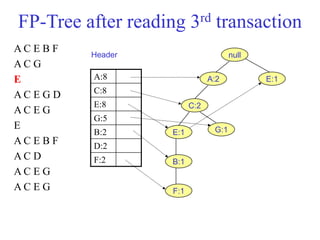
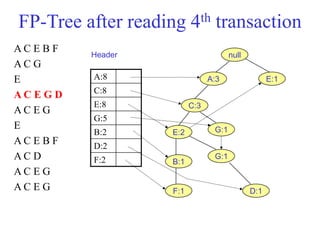
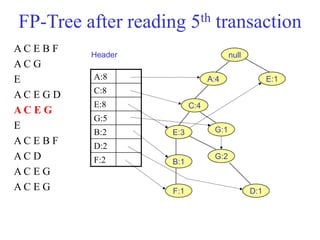
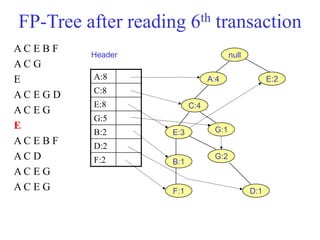
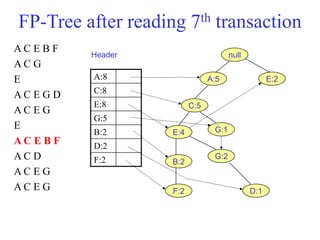
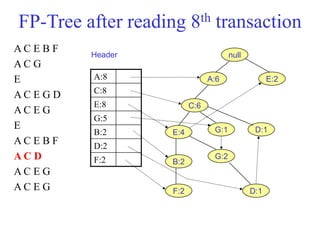
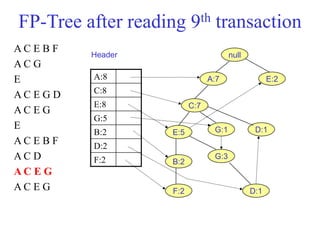
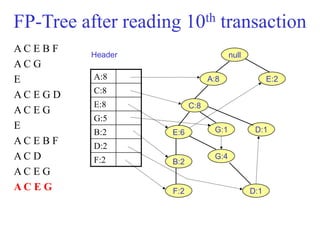
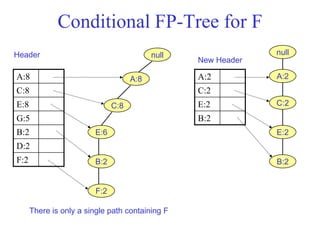
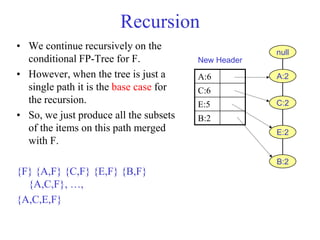
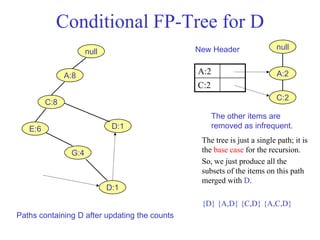
The document discusses the Eclat algorithm for mining frequent itemsets, highlighting its methodology and advantages, including faster support counting compared to the Apriori algorithm. It details the construction of transaction ID tables and the use of vertical data layouts for efficient itemset generation. The document also covers the construction and traversal of FP-trees in the FP-Growth algorithm for deriving frequent itemsets recursively.

1. ALGORITMA ECLAT
SERTI LONDONGALLO
KRISTI W. SAIYA
BRYAN NAWANJAYA ARTIKA
ABADI GUNAWAN AZIS
B:8
A:5
null
C:3
D:1
A:2
C:1
D:1
E:1
D:1
E:1C:3
D:1
D:1 E:1

2. Metode Pencarian Alternatif
• Gambaran penyilangan Itemset Lattice
– Umum-Khusus vs Khusus-Umum
Frequent
itemset
border null
{a1,a2,...,an}
(a) General-to-specific
null
{a1,a2,...,an}
Frequent
itemset
border
(b) Specific-to-general
..
..
..
..
Frequent
itemset
border
null
{a1,a2,...,an}
(c) Bidirectional
..
..
Apriori Eclat ???

3. • Gambaran penyilangan Itemset Lattice
– Breadth-first(Menyeluruh) vs Depth-first(Mendalam)
(a) Breadth first (b) Depth first
Metode Pencarian Alternatif

4. ECLAT: Metode Pembentukan Itemset
• ECLAT: untuk setiap item, dinyatakan dalam tabel
transaction ids (tids); tampilan data vertikal
TID Items
1 A,B,E
2 B,C,D
3 C,E
4 A,C,D
5 A,B,C,D
6 A,E
7 A,B
8 A,B,C
9 A,C,D
10 B
Horizontal
Data Layout
A B C D E
1 1 2 2 1
4 2 3 4 3
5 5 4 5 6
6 7 8 9
7 8 9
8 10
9
Vertical Data Layout
TID-list

5. ECLAT: Metode Pembentukan Itemset
• Tentukan support (pendukung) dari setiap k-itemset dengan
menyilangkan tid-lists dari kedua (k-1) subset.
• 3 pendekatan penyilangan:
– Atas-bawah, bawah-atas dan gabungan
• Keuntungan: Proses hitung support lebih cepat dibandingkan
algoritma apriori
• Kerugian: ukuran tid (vertikal) lebih besar dibandingkan
apriori, sehingga memenuhi memori
A
1
4
5
6
7
8
9
B
1
2
5
7
8
10
 
AB
1
5
7
8

6. First scan – determine frequent 1-
itemsets, then build header
TID Items
1 {A,B}
2 {B,C,D}
3 {A,C,D,E}
4 {A,D,E}
5 {A,B,C}
6 {A,B,C,D}
7 {B,C}
8 {A,B,C}
9 {A,B,D}
10 {B,C,E}
B 8
A 7
C 7
D 5
E 3

7. FP-tree construction
TID Items
1 {A,B}
2 {B,C,D}
3 {A,C,D,E}
4 {A,D,E}
5 {A,B,C}
6 {A,B,C,D}
7 {B,C}
8 {A,B,C}
9 {A,B,D}
10 {B,C,E}
null
B:1
A:1
After reading TID=1:
After reading TID=2:
null
B:2
A:1
C:1
D:1

8. FP-Tree Construction
TID Items
1 {A,B}
2 {B,C,D}
3 {A,C,D,E}
4 {A,D,E}
5 {A,B,C}
6 {A,B,C,D}
7 {B,C}
8 {A,B,C}
9 {A,B,D}
10 {B,C,E}
Transaction
Database
Item Pointer
B 8
A 7
C 7
D 5
E 3
Header table
B:8
A:5
null
C:3
D:1
A:2
C:1
D:1
E:1
D:1
E:1C:3
D:1
D:1 E:1
Chain pointers help in quickly finding all the paths
of the tree containing some given item.

9. FP-Growth (I)
• FP-growth generates frequent itemsets from an FP-tree by
exploring the tree in a bottom-up fashion.
• Given the example tree, the algorithm looks for frequent
itemsets ending in E first, followed by D, C, A, and finally, B.
• Since every transaction is mapped onto a path in the FP-tree, we
can derive the frequent itemsets ending with a particular item,
say, E, by examining only the paths containing node E.
• These paths can be accessed rapidly using the pointers
associated with node E.

10. Paths containing node E
B:3
null
C:3
A:2
C:1
D:1
E:1
D:1
E:1E:1
B:8
A:5
null
C:3
D:1
A:2
C:1
D:1
E:1
D:1
E:1C:3
D:1
D:1 E:1

11. Conditional FP-Tree for E
• We now need to build a conditional FP-Tree for E, which is the
tree of itemsets include in E.
• It is not the tree obtained in previous slide as result of deleting
nodes from the original tree.
• Why? Because the order of the items change.
– In this example, D has a higher than E count.

12. Conditional FP-Tree for E
Adding up the counts for D we get
2, so {E,D} is frequent itemset.
We continue recursively.
Base of recursion: When the tree
has a single path only.
B:3
null
C:3
A:2
C:1
D:1
E:1
D:1
E:1E:1
The set of paths containing E.
Insert each path (after truncating
E) into a new tree.
Item Pointer
C 4
B 3
A 2
D 2
Header table
The new
header
C:3
null
B:3
C:1
A:1
D:1
A:1
D:1
The
conditional
FP-Tree for E

13. FP-Tree Another Example
A B C E F O
A C G
E I
A C D E G
A C E G L
E J
A B C E F P
A C D
A C E G M
A C E G N
A:8
C:8
E:8
G:5
B:2
D:2
F:2
A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
Freq. 1-Itemsets.
Supp. Count 2
Transactions Transactions with items sorted based
on frequencies, and ignoring the
infrequent items.

14. FP-Tree after reading 1st transaction
A:8
C:8
E:8
G:5
B:2
D:2
F:2
A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
null
A:1
C:1
E:1
B:1
F:1
Header

15. FP-Tree after reading 2nd transaction
A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:2
C:2
E:1
B:1
F:1
Header

16. FP-Tree after reading 3rd transaction
A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:2
C:2
E:1
B:1
F:1
Header
E:1

17. A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
FP-Tree after reading 4th transaction
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:3
C:3
E:2
B:1
F:1
Header
E:1
G:1
D:1

18. A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
FP-Tree after reading 5th transaction
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:4
C:4
E:3
B:1
F:1
Header
E:1
G:2
D:1

19. A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
FP-Tree after reading 6th transaction
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:4
C:4
E:3
B:1
F:1
Header
E:2
G:2
D:1

20. A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
FP-Tree after reading 7th transaction
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:5
C:5
E:4
B:2
F:2
Header
E:2
G:2
D:1

21. A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
FP-Tree after reading 8th transaction
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:6
C:6
E:4
B:2
F:2
Header
E:2
G:2
D:1
D:1

22. A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
FP-Tree after reading 9th transaction
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:7
C:7
E:5
B:2
F:2
Header
E:2
G:3
D:1
D:1

23. A C E B F
A C G
E
A C E G D
A C E G
E
A C E B F
A C D
A C E G
A C E G
FP-Tree after reading 10th transaction
G:1
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:8
C:8
E:6
B:2
F:2
Header
E:2
G:4
D:1
D:1

24. Conditional FP-Tree for F
A:8
C:8
E:8
G:5
B:2
D:2
F:2
null
A:8
C:8
E:6
B:2
F:2
Header
There is only a single path containing F
A:2
C:2
E:2
B:2
null
A:2
C:2
E:2
B:2
New Header

25. Recursion
• We continue recursively on the
conditional FP-Tree for F.
• However, when the tree is just a
single path it is the base case for
the recursion.
• So, we just produce all the subsets
of the items on this path merged
with F.
{F} {A,F} {C,F} {E,F} {B,F}
{A,C,F}, …,
{A,C,E,F}
A:6
C:6
E:5
B:2
null
A:2
C:2
E:2
B:2
New Header

26. Conditional FP-Tree for D
A:2
C:2
null
A:2
C:2
New Headernull
A:8
C:8
E:6
G:4
D:1
D:1
Paths containing D after updating the counts
The other items are
removed as infrequent.
The tree is just a single path; it is
the base case for the recursion.
So, we just produce all the
subsets of the items on this path
merged with D.
{D} {A,D} {C,D} {A,C,D}