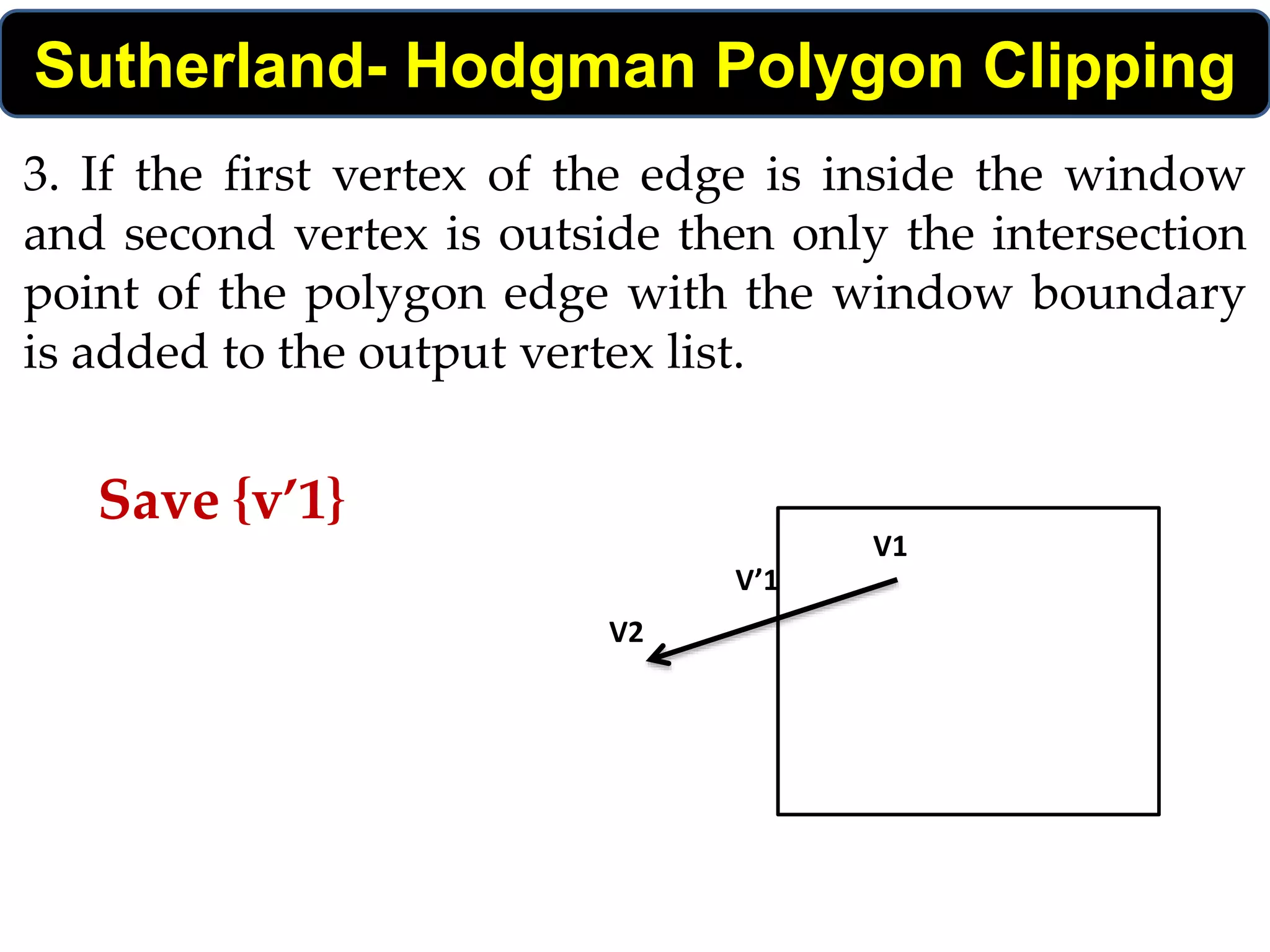
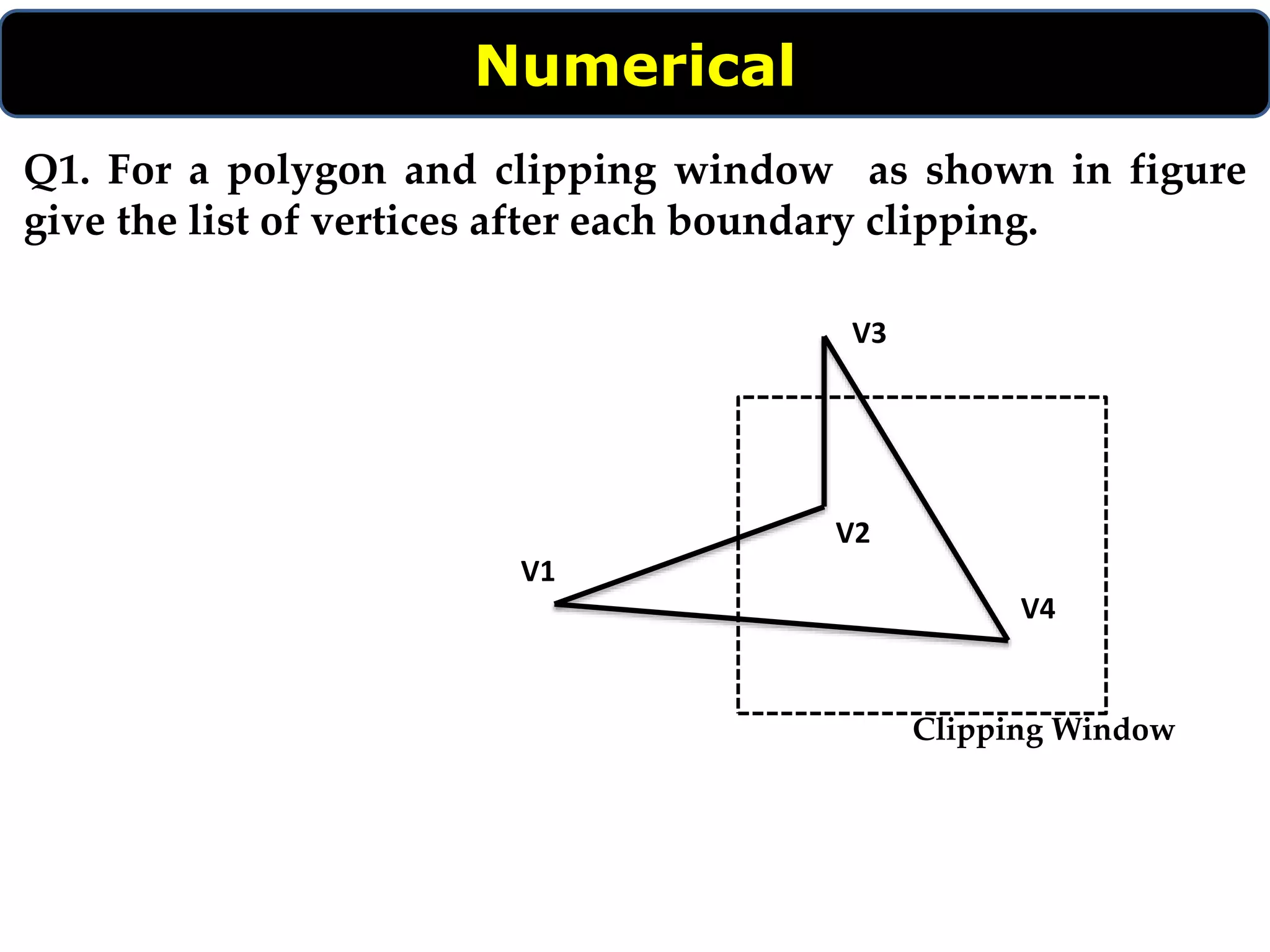
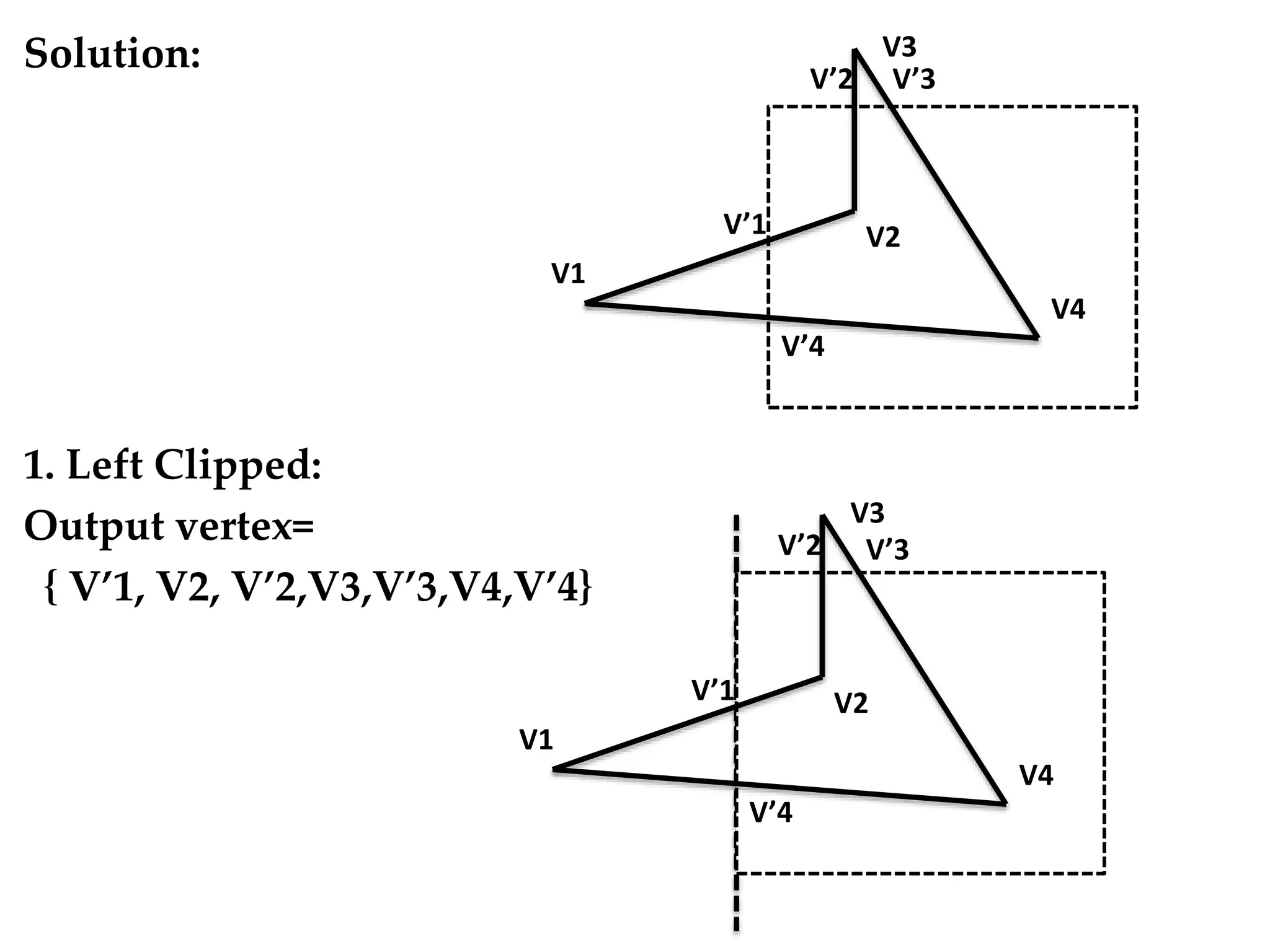
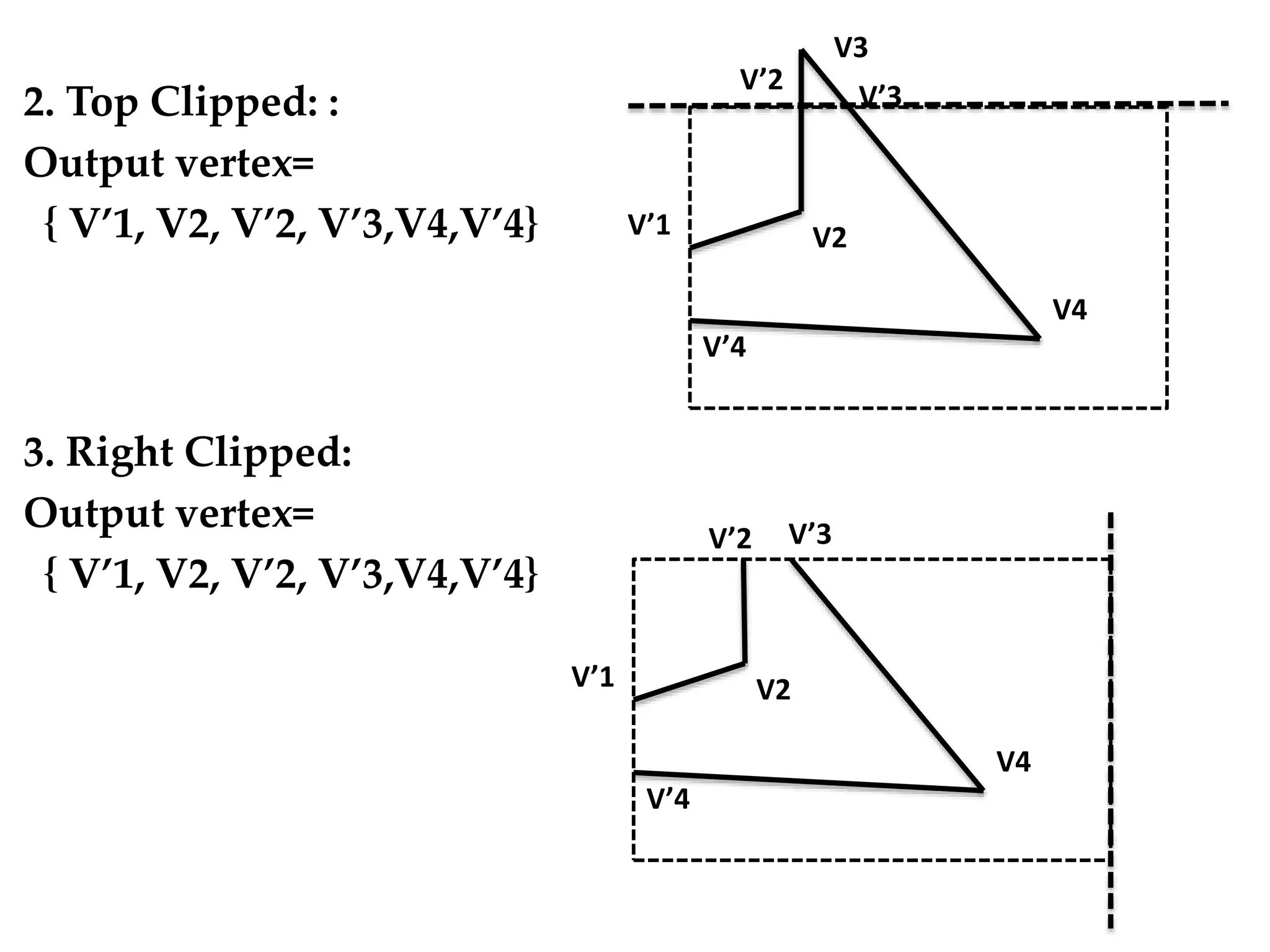
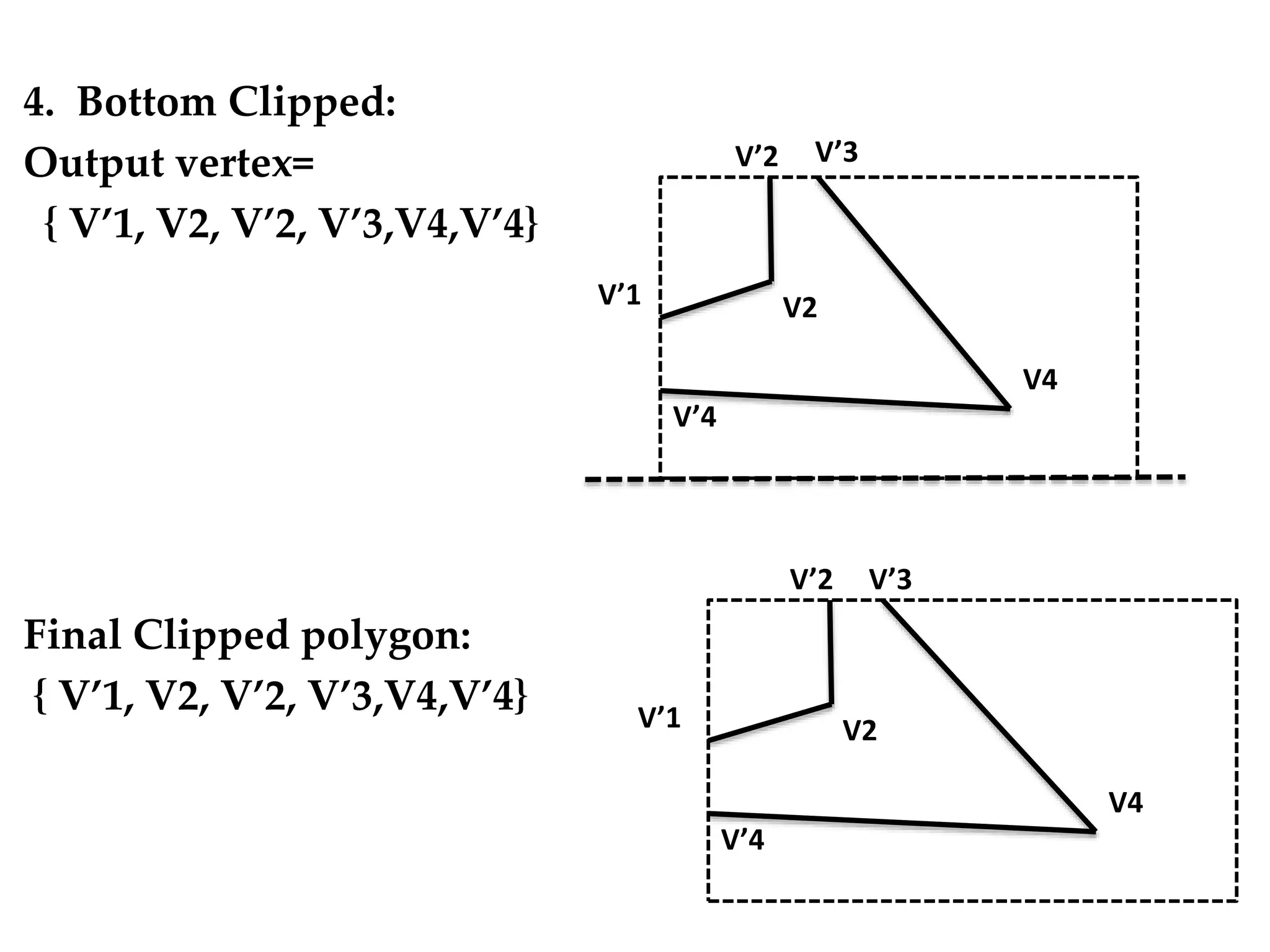
The Sutherland-Hodgman algorithm clips polygons by clipping against each edge of the clipping window in a specific order: left, top, right, bottom. It works by testing each edge of the polygon against the clipping window boundary and either keeping or discarding vertices based on whether they are inside or outside the window. The algorithm results in a clipped polygon that only includes vertices and edge intersections that are inside the clipping window.

1. Computer Graphics
Sutherland - Hodgman
(Polygon Clipping)
Covered by:-
Arvind Kumar
Assistant Professor
Vidya College of Engg.

2. Sutherland- Hodgman Polygon Clipping
The Sutherland-Hodgman algorithm performs a
clipping of a polygon against each window edge in
turn.
The order to clip the polygon should be:
1. Clipping against the left side of the clip window.
2. Clipping against the top side of the clip window.
3. Clipping against the right side of the clip window.
4. Clipping against the bottom side of the clip window.

3. Sutherland- Hodgman Polygon Clipping
After Clipped

4. Sutherland- Hodgman Polygon Clipping
It consist of Four Cases:
1. If the first vertex of the edge is outside the window
and second vertex is inside then the intersection
point of the polygon edge with the window
boundary and the second vertex are added to the
output vertex list.
Save {v’1 and v2} V1
V’1
V2

5. Sutherland- Hodgman Polygon Clipping
2. If the both vertices of the edge are inside the
window. Then only second vertex is added to the
output vertex list.
Save {v2}
V1
V2

6. Sutherland- Hodgman Polygon Clipping
3. If the first vertex of the edge is inside the window
and second vertex is outside then only the intersection
point of the polygon edge with the window boundary
is added to the output vertex list.
Save {v’1}
V2
V’1
V1

7. Sutherland- Hodgman Polygon Clipping
4. If the both vertices of the edge are outside the
window. Then nothing is added to the output vertex
list.
Save {∅}
V1
V2

8. Numerical
Q1. For a polygon and clipping window as shown in figure
give the list of vertices after each boundary clipping.
Clipping Window
V1
V2
V3
V4

9. Solution:
1. Left Clipped:
Output vertex=
{ V’1, V2, V’2,V3,V’3,V4,V’4}
V’3
V1
V2
V3
V4
V’1
V’2
V’4
V1
V2
V3
V4
V’1
V’2
V’4
V’3

10. 2. Top Clipped: :
Output vertex=
{ V’1, V2, V’2, V’3,V4,V’4}
3. Right Clipped:
Output vertex=
{ V’1, V2, V’2, V’3,V4,V’4}
V’3
V2
V3
V4
V’1
V’2
V’4
V2
V4
V’1
V’2
V’4
V’3

11. 4. Bottom Clipped:
Output vertex=
{ V’1, V2, V’2, V’3,V4,V’4}
Final Clipped polygon:
{ V’1, V2, V’2, V’3,V4,V’4}
V2
V4
V’1
V’2
V’4
V’3
V2
V4
V’1
V’2
V’4
V’3