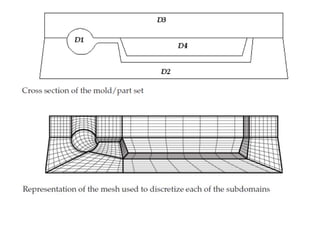
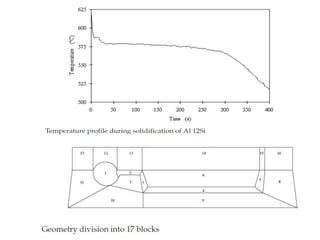
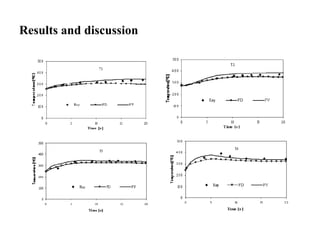
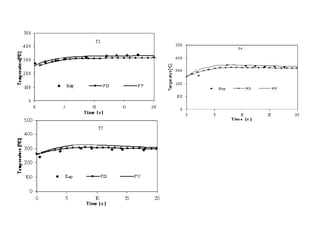
This document presents a numerical study comparing finite difference and finite volume methods for solving the heat transfer equation during solidification in a complex casting geometry. The study uses a multi-block grid with bilinear interpolation and generalized curvilinear coordinates. Results show good agreement between the two discretization methods, with a slight advantage for the finite volume method due to its use of more nodal information. The multi-block grid approach reduces computational time and allows complex geometries to be accurately modeled while overcoming issues at block interfaces.

1. NUMERICAL METHODS FOR
2-D HEAT TRANSFER
KARTHIKA M
202112010
CHEMICAL ENGINEERING
19.04.2013

2. • Due to the increasing complexities
encountered in the development of modern
technology, analytical solutions usually are not
available.
• For these problems, numerical solutions
obtained using high-speed computer are very
useful, especially when the geometry of the
object of interest is irregular, or the boundary
conditions are nonlinear.

3. 
Numerical methods are necessary to solve many practical
problems in heat conduction that involve:
– complex 2D and 3D geometries
– complex boundary conditions
– variable properties

An appropriate numerical method can produce a useful
approximate solution to the temperature field T(x,y,z,t); the
method must be
– sufficiently accurate
– stable
– computationally efficient

4. General Features





A numerical method involves a discretization process, where
the solution domain is divided into subdomains and nodes
The PDE that describes heat conduction is replaced by a
system of algebraic equations, one for each subdomain in
terms of nodal temperatures
A solution to the system of algebraic equations almost always
requires the use of a computer
As the number of nodes (or subdomains) increase, the
numerical solution should approach the exact solution
Numerical methods introduce error and the possibility of
solution instability

5. Types of Numerical Methods
1. The Finite Difference Method (FDM)
– subdomains are rectangular and nodes form a
regular grid network
– nodal values of temperature constitute the
numerical solution; no interpolation functions are
included
– discretization equations can be derived from
Taylor series expansions or from a control volume
approach

6. 2. The Finite Element Method (FEM)
– subdomain may be any polygon shape, even with
curved sides; nodes can be placed anywhere in
subdomain
– numerical solution is written as a finite series sum
of interpolation functions, which may be linear,
quadratic, cubic, etc.
– solution provides nodal temperatures and
interpolation functions for each subdomain

7. • In heat transfer problems, the finite difference method
is used more often and will be discussed here.
• The finite difference method involves:
 Establish nodal networks
 Derive finite difference approximations for the
governing equation at both interior and exterior nodal
points
 Develop a system of simultaneous algebraic nodal
equations
 Solve the system of equations using numerical schemes

8. The Nodal Networks
The basic idea is to subdivide the area of interest into sub-volumes with the distance
between adjacent nodes by Dx and Dy as shown. If the distance between points is small
enough, the differential equation can be approximated locally by a set of finite difference
equations. Each node now represents a small region where the nodal temperature is a
measure of the average temperature of the region.
Example:
Dx
m,n+1
m-1,n
m,n
m+1, n
Dy
m,n-1
x=mDx, y=nDy
m+½,n
m-½,n
intermediate points

9. Finite Difference Approximation
q 1 T
Heat Diffusion Equation:  T  
,
k  t
k
where  =
is the thermal diffusivity
 C PV
2

No generation and steady state: q=0 and
 0,  2T  0
t
First, approximated the first order differentiation
at intermediate points (m+1/2,n) & (m-1/2,n)
T
DT

x ( m 1/ 2,n ) Dx
T
DT

x ( m 1/ 2,n ) Dx
( m 1/ 2,n )
Tm 1,n  Tm ,n

Dx
( m 1/ 2,n )
Tm ,n  Tm 1,n

Dx

10. Finite Difference Approximation (cont.)
Next, approximate the second order differentiation at m,n
 2T
x 2
 2T
x 2

m ,n
m ,n
T / x m 1/ 2,n  T / x m 1/ 2,n
Dx
Tm 1,n  Tm 1,n  2Tm ,n

( Dx ) 2
Similarly, the approximation can be applied to
the other dimension y
 2T
y 2
m ,n
Tm ,n 1  Tm ,n 1  2Tm ,n

( Dy ) 2

11. Finite Difference Approximation (cont.)
Tm 1,n  Tm 1,n  2Tm ,n Tm ,n 1  Tm ,n 1  2Tm ,n
  2T  2T 

 x 2  y 2  
2
( Dx )
( Dy ) 2

 m ,n
To model the steady state, no generation heat equation: 2T  0
This approximation can be simplified by specify Dx=Dy
and the nodal equation can be obtained as
Tm 1,n  Tm 1,n  Tm ,n 1  Tm ,n 1  4Tm ,n  0
This equation approximates the nodal temperature distribution based on
the heat equation. This approximation is improved when the distance
between the adjacent nodal points is decreased:
DT T
DT T
Since lim( Dx  0)

,lim( Dy  0)

Dx x
Dy y

12. A System of Algebraic Equations
• The nodal equations derived previously are valid for all interior
points satisfying the steady state, no generation heat equation.
For each node, there is one such equation.
For example: for nodal point m=3, n=4, the equation is
T2,4 + T4,4 + T3,3 + T3,5 - 4T3,4 =0
T3,4=(1/4)(T2,4 + T4,4 + T3,3 + T3,5)
• Derive one equation for each nodal point (including both
interior and exterior points) in the system of interest. The result is
a system of N algebraic equations for a total of N nodal points.

13. Matrix Form
The system of equations:
a11T1  a12T2   a1N TN  C1
a21T1  a22T2 
 a2 N TN  C2
a N 1T1  a N 2T2 
 a NN TN  CN
A total of N algebraic equations for the N nodal points and the system can be
expressed as a matrix formulation: [A][T]=[C]
 a11 a12
a
a22
21
where A= 


aN 1 aN 2
a1N 
 T1 
 C1 
T 
C 
a2 N 
 , T   2  ,C   2 

 
 

 
 
aNN 
TN 
C N 

14. Numerical Solutions
Matrix form: [A][T]=[C].
From linear algebra: [A]-1[A][T]=[A]-1[C], [T]=[A]-1[C]
where [A]-1 is the inverse of matrix [A]. [T] is the solution vector.
• Matrix inversion requires cumbersome numerical computations and is not efficient if
the order of the matrix is high (>10).
• For high order matrix, iterative methods are usually more efficient. The famous
Jacobi & Gauss-Seidel iteration methods will be introduced in the following.

15. Iteration
General algebraic equation for nodal point:
i 1
a T
j 1
ij
j
 aiiTi 
N
aT
j i 1
ij
j
 Ci ,
(Example : a31T1  a32T2  a33T3 
 a1N TN  C1 , i  3)
Rewrite the equation of the form:
N
aij ( k 1)
Ci i 1 aij ( k )
(k )
Ti    T j   T j
aii j 1 aii
j i 1 aii
Replace (k) by (k-1)
for the Jacobi iteration
• (k) - specify the level of the iteration, (k-1) means the present level and (k) represents
the new level.
• An initial guess (k=0) is needed to start the iteration.
• By substituting iterated values at (k-1) into the equation, the new values at iteration
(k) can be estimated
• The iteration will be stopped when maxTi(k)-Ti(k-1), where  specifies a
predetermined value of acceptable error

16. CASE STUDY
Finite Volume Method Analysis of Heat Transfer in
Multi-Block Grid During Solidification
Eliseu Monteiro1, Regina Almeida2 and Abel Rouboa3
1CITAB/UTAD - Engineering Department of
University of Tr´as-os-Montes e Alto Douro, Vila Real
2CIDMA/UA - Mathematical Department of
University of Tr´as-os-Montes e Alto Douro, Vila Real
3CITAB/UTAD - Department of Mechanical Engineering and
Applied Mechanics of University of Pennsylvania,
Philadelphia, PA
1,2Portugal
3USA

17. The governing differential equation for the solidification problem may
be written in the following conservative form
∂ (ρCPφ)
∂t
= ∇· (k∇φ) + q˙
(1)
where ∂(ρCPφ) ∂t represents the transient contribution to the
conservative energy equation (φ temperature); ∇· (k∇φ) is the
diffusive contribution to the energy equation and q˙ represents the
energy released during the phase change.

18. undary conditions

19. Numerical solution method
• Finite volume method

21. Finite difference method

24. Results and discussion

26. • Iterative performance of the three different
numerical methods are also given.

27. Concluding remarks
A multi-block grid generated by bilinear interpolation was successfully applied in
combination with a generalized curvilinear coordinates system to a complex
geometry in a casting solidification scenario. To model the phase change a
simplified two dimensional mathematical model was used based on the energy
differential equation. Two discretization methods: finite differences and finite
volume were applied in order to determine, by comparison with experimental
measurements, which works better in these conditions. For this reason a coarse
grid was used. A good agreement between both discretization methods was
obtained with a slight advantage for the finite volume method. This could be
explained due to the use of more information by the finite volume method to
compute each temperature value than the finite differences method. The multiblock grid in combination with a generalized curvilinear coordinates system has
considerably advantages such as:

28. • better capacity to describe the contours through a lesser
number of elements, which considerably reduces the
computational time;
• - any physical feature of the cast part or mold can be
straightforwardly defined and obtained in a specific zone of
the domain;
• - the difficulty of the several virtual interfaces created by the
geometry division are easily overcome by the continuity
condition

29. THANK YOU