This document details a numerical methods lab work focused on using Fortran to solve a simple heat equation for a copper rod under two boundary conditions: Dirichlet and von Neumann. The lab involves applying finite difference methodologies to analyze temperature variations at different nodes of the rod over time, highlighting stability concerns with various values of the finite difference parameter 'c'. It concludes with insights gained from the project and references for further learning about Fortran.

1. Numerical Methods Lab Work 2
By
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh
Submitted to
KOZHANOVA Ksenia

2. ABSTRACT
FORTRAN is used as a numerical and scientific computing language. The main objective
of the lab work is to understand FORTRAN language using which we solve simple
numerical problems and compare different methodologies. Through this project we make
use of various functions of FORTRAN and solve a FDM simple heat equation problem
applying different conditions viz. Dirichlet and Von Neumann. The given problems are
solved analytically then built and compiled using a free integrated development
environment called CODE::BLOCKS [1] which is an open source platform for FORTRAN
and C.

3. CONTENTS:
List of figures.
1. A simple heat flow experiment using 1D Heat Equation. 1
2. Finite Difference Explicit Method. 2
3. Finite Difference Implicit Method. 9
CONCLUSION 11
REFERENCE 12

4. LIST OF FIGURES.
 Fig 1: Rod considered for the problem.
Dirichlet Boundary,
 Fig 2: Temperature variation at each node of c value 0.25
 Fig 3: Temperature variation at each node of C value 0.49
 Fig 4: Temperature variation at each node of C value 0.51
 Fig 5: Temperature variation at each node of C value 0.75
Von Neumann Boundary,
 Fig 6: Temperature variation at each node of C value 0.25
 Fig 7: Temperature variation at each node of C value 0.49
 Fig 8: Temperature variation at each node of C value 0.55
 Fig 9: Temperature variation at each node of C value 0.75

5. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 1 | P a g e
1. A simple heat flow experiment using 1D Heat Equation.
A Copper rod of length L = 1m and diameter is 1 cm with lateral sides insulated is subjected to
external temperature T0, until the temperature of the rod reaches T0. At time t=0, the ends of the rod
are subjected to T1 and T2 temperature with the given boundary conditions solve the heat equation
and write in non-dimensional form.
Fig 1: Rod considered for the problem.
Initial and boundary conditions,
T (0, x) = T0 = 400 Initial
T(t,0) = T1 = 300 Dirichlet condition
T (t, L) = T2 = 500 Dirichlet condition
𝜌𝐶 𝑝
𝜕𝑇
𝜕𝑡
+
𝜕
𝜕𝑥
(−𝜆
𝜕𝑇
𝜕𝑥
) = 0 ………….(1)
Where,
𝝆 is Density (kg/m3
)
Cp is the Heat capacity
𝝀 is the conductivity.
Assuming 𝜆 as constant equation 1 can be written as,
𝜕𝑇
𝜕𝑡
= 𝛼
𝜕2 𝑇
𝜕𝑥2 ……………..(2)
Where,
𝛼 =
𝜆
𝜌𝐶 𝑝
Non Dimensionalization of the equation,
𝑇̃ = T
𝑥̃ = x
𝑡̃ = t

6. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 2 | P a g e
𝜕𝑇̃
𝜕𝑡̃
=
𝜕2
𝑇̃
𝜕𝑥̃2
2. Finite Difference Explicit Method:
Using second order centered difference for space derivative and simple first order forward
difference for time derivative. The scheme results in,
𝜕 = T (t + 𝛥𝑡) - T (t)
𝜕𝑡 𝛥𝑡
Using the above scheme,
∂T
∂t
=
Tj
k+1
−Tj
k
∆t
.………………... (3)
Substituting the equation no. 3,
𝜕2 𝑇
𝜕𝑥2 =
𝑇𝑗+1
𝑘
−2𝑇𝑗
𝑘
+𝑇𝑗−1
𝑘
(∆𝑥)2 …………. (4)
Using the equation no. 3 and 4,
𝑇𝑗
𝑘+1
− 𝑇𝑗
𝑘
=
∆𝑡
∆𝑥2 (𝑇𝑗+1
𝑘
− 2𝑇𝑗
𝑘
+ 𝑇𝑗−1
𝑘
) ………. (5)
Considering,
𝑐 =
∆𝑡
∆𝑥2
This equation helps in finding the temperature evolution at different stages,
𝑻𝒋
𝒌+𝟏
= 𝒄. 𝑻𝒋−𝟏
𝒌
+ (𝟏 − 𝟐𝒄)𝑻𝒋
𝒌
+ 𝒄. 𝑻𝒋+𝟏
𝒌
Discretizing Boundary conditions:
Boundary conditions and initial conditions for the problem is given for two cases. Imposed
temperature in the two ends of the rod,
T(1,t)=300 indicating 𝑻 𝟏
𝒌
= 𝟑𝟎𝟎
T(L,t)=500 indicating 𝑻 𝑵
𝒌
= 𝟓𝟎𝟎

7. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 3 | P a g e
The initial condition is T(x, 1) = 400 indicating 𝑇𝑗
1
= 400
Applying the boundary conditions in the obtained equation 5 with j varying from 2 to N-1
𝑇𝑗
𝑘+1
= 𝑐𝑇𝑗−1
𝑘
+ (1 − 2𝑐)𝑇𝑗
𝑘
+ 𝑐𝑇𝑗+1
𝑘
The equation for the second node can be written as,
𝑇2
𝑘+1
= 𝑐𝑇1
𝑘
+ (1 − 2𝑐)𝑇2
𝑘
+ 𝑐𝑇3
𝑘
𝑇2
𝑘+1
= 300𝑐 + (1 − 2𝑐)𝑇2
𝑘
+ 𝑐𝑇3
𝑘
The equation for the last but one node can be written as,
𝑇 𝑁−1
𝑘+1
= 𝑐𝑇 𝑁−2
𝑘
+ (1 − 2𝑐)𝑇 𝑁−1
𝑘
+ 𝑐𝑇 𝑁
𝑘
𝑇 𝑁−1
𝑘+1
= 𝑐𝑇 𝑁−2
𝑘
+ (1 − 2𝑐)𝑇 𝑁−1
𝑘
+ 500𝑐
Writing the system of equations in the matrix form:
𝑻 𝒌+𝟏
= 𝑨𝑻 𝒌
+ 𝑩
(
𝑇1
𝑘+1
⋮
𝑇 𝑁
𝑘+1
) = [
1 − 2𝑐 𝑐 0
𝑐 ⋱ ⋱
0 ⋱ 1 − 2𝑐
] (
𝑇1
𝑘
⋮
𝑇 𝑁
𝑘
) + [
300
⋮
500
]
Here (1-2c) occupies the main diagonal and c the lower and upper diagonal. B is the boundary
condition matrix with only two entries at the extreme nodes and the other values are 0.
By applying the derived equation into program graphs for temperature values as function of time for
different length divisions can be obtained.

8. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 4 | P a g e
Fig 2: Temperature variation at each node of c value 0.25
Fig 3: Temperature variation at each node of C value 0.49
As shown in the graphs 1 and 2 the temperature at each node after some amount of time converges
showing that it gains equilibrium. This is considered true only when c value is less than 0.5 which is
evident from the graph 3 and 4. As c increased to 0.5, the system became marginally stable. The
reason of referring the system has been deduced from unstable solutions where c takes a value above
0.5.
290
340
390
440
490
-0.15 0.05 0.25 0.45 0.65 0.85 1.05
Temparature(K)
LENGTH (L)
C = 0.25
270
320
370
420
470
-0.15 0.05 0.25 0.45 0.65 0.85 1.05
Temperature(K)
LENGTH (L)
C = 0.49

9. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 5 | P a g e
Fig 4: Temperature variation at each node of C value 0.51
Fig 5: Temperature variation at each node of C value 0.75
For values of c > 0.5, the system becomes unstable. The resulting graphs are varying and dissimilar
when compared to graphs of stable system. Oscillations in temperature curves can be seen as time
progress occurs, which indicates instability in the system. In c = 0.75, instabilities begin to start
earlier which say that as c is increased further, oscillations occur rapidly.
Von Neumann Boundary condition:
Imposed temperature on one end of the rod and a flux on another end of the rod,
T (1, t) = 300 indicating,
-2E+30
-1.5E+30
-1E+30
-5E+29
0
5E+29
1E+30
1.5E+30
2E+30
-0.15 0.05 0.25 0.45 0.65 0.85 1.05
Temperature(K)
LENGTH (L)
C = 0.51
-4E+38
-3E+38
-2E+38
-1E+38
0
1E+38
2E+38
3E+38
4E+38
-0.15 0.05 0.25 0.45 0.65 0.85 1.05
Temperature(K)
LENGTH (L)
C = 0.75

10. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 6 | P a g e
𝑇1
𝑘
= 300 𝑎𝑛𝑑
𝜕𝑇( 𝑡, 𝐿)
𝜕𝑥
= 50
This temperature is maintained at all time in this problem. The initial condition is same as the
previous case given by T(x, 1) = 400 indicating 𝑇𝑗
1
= 400
Applying the boundary conditions in the obtained with j varying from 2 to N-1:
𝑇𝑗
𝑘+1
= 𝑐𝑇𝑗−1
𝑘
+ (1 − 2𝑐)𝑇𝑗
𝑘
+ 𝑐𝑇𝑗+1
𝑘
The equation for the second node is same as the previous case:
𝑇2
𝑘+1
= 300𝑐 + (1 − 2𝑐)𝑇2
𝑘
+ 𝑐𝑇3
𝑘
The equation for the second last node using the Von Neumann boundary condition:
𝜕𝑇(𝑡, 𝐿)
𝜕𝑥
= 50
Is expressed using backward scheme as follows:
𝑇 𝑁
𝑘
= 50𝛥𝑥 + 𝑇 𝑁−1
𝑘
We get the final equation as∶
𝑇 𝑁−1
𝑘+1
= 𝑐𝑇 𝑁−2
𝑘
+ (1 − 2𝑐)𝑇2
𝑘
+ 50𝛥𝑥 + 𝑇 𝑁−1
𝑘
Applying center difference scheme to the boundary conditions we get,
𝜕𝑇
𝜕𝑥
=
𝑇𝑛+1
𝑘
− 𝑇𝑛−1
𝑘
2∆𝑥
= 50
Where 𝑇𝑛+1
𝑘
= 100 × ∆𝑥 + 𝑇𝑛−1
𝑘
is a ghost node that updates the values of Tn in the
equation.
By applying the derived equation into program graphs for temperature values as function of time for
different length divisions can be obtained.

11. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 7 | P a g e
Fig 6: Temperature variation at each node of C value 0.25
Fig 7: Temperature variation at each node of C value 0.49
290
310
330
350
370
390
410
430
0 0.2 0.4 0.6 0.8 1
Temperature(K)
LENGTH (L)
C = 0.25
290
310
330
350
370
390
410
430
0 0.2 0.4 0.6 0.8 1
Temperature(K)
LENGTH (L)
C = 0.49

12. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 8 | P a g e
Fig 8: Temperature variation at each node of C value 0.55
Fig 9: Temperature variation at each node of C value 0.75
From the obtained graphs, it can be seen that the effect of the Von Neumann boundary condition on
right end of the bar is observed from the plots. The temperature value at this end is drastically
decreased comparing with that of Dirichlet boundary condition. It can be observed that the solution
of temperature variation for von Neumann condition takes more time to intersect compared to
Dirichlet. From the stability point of view, for values of c > 0.5, oscillations occur with increasing
time resulting in instability.
-2.5E+38
-2E+38
-1.5E+38
-1E+38
-5E+37
0
5E+37
1E+38
1.5E+38
2E+38
2.5E+38
-0.15 0.05 0.25 0.45 0.65 0.85 1.05
Temperature(K)
LENGTH (L)
C = 0.55
-3E+15
-2E+15
-1E+15
0
1E+15
2E+15
3E+15
-0.15 0.05 0.25 0.45 0.65 0.85 1.05
Temperature(K)
LENGTH (L)
C = 0.75

13. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 9 | P a g e
3. Finite difference implicit method:
In this method, the forward difference scheme is applied for time derivative and center second
difference scheme is applied for space derivative for the next time step as follows.
𝜕𝑇
𝜕𝑡
=
𝑇𝑗
𝑘+1
− 𝑇𝑗
𝑘
∆𝑡
𝜕2
𝑇
𝜕𝑥2
=
𝑇𝑗+1
𝑘+1
− 2𝑇𝑗
𝑘+1
+ 𝑇𝑗−1
𝑘+1
(∆𝑥)2
Substituting the above equations in the equation no. 1, and considering,
𝑐 =
∆𝑡
(∆𝑥)2,
The following equation is obtained,
𝑻(𝒌) = −𝒄. 𝑻𝒋−𝟏
𝒌+𝟏
+ (𝟏 + 𝟐𝒄)𝑻𝒋
𝒌+𝟏
− 𝒄. 𝑻𝒋+𝟏
𝒌+𝟏
……………(6)
The following boundary conditions are applied to the above stated equation. Boundary conditions
and initial conditions for the problem is given for two cases. Imposed temperature in the two ends
of the beam,
T(1,t)=300 indicating 𝑻 𝟏
𝒌
= 𝟑𝟎𝟎
T(L,t)=500 indicating 𝑻 𝑵
𝒌
= 𝟓𝟎𝟎
This temperature is maintained at all times for this problem. The initial condition is T(x, 1) =400
indicating 𝑻𝒋
𝟏
= 𝟒𝟎𝟎
Applying the boundary conditions in the obtained equation 6 with j varying from 2 to N-1
𝑇𝑗
𝑘
= −𝑐𝑇𝑗−1
𝑘+1
+ (1 + 2𝑐)𝑇𝑗
𝑘+1
− 𝑐𝑇𝑗+1
𝑘+1
The equation for the second node can be written as,
𝑇2
𝑘
= −𝑐𝑇1
𝑘+1
+ (1 + 2𝑐)𝑇2
𝑘+1
+ 𝑐𝑇3
𝑘+1

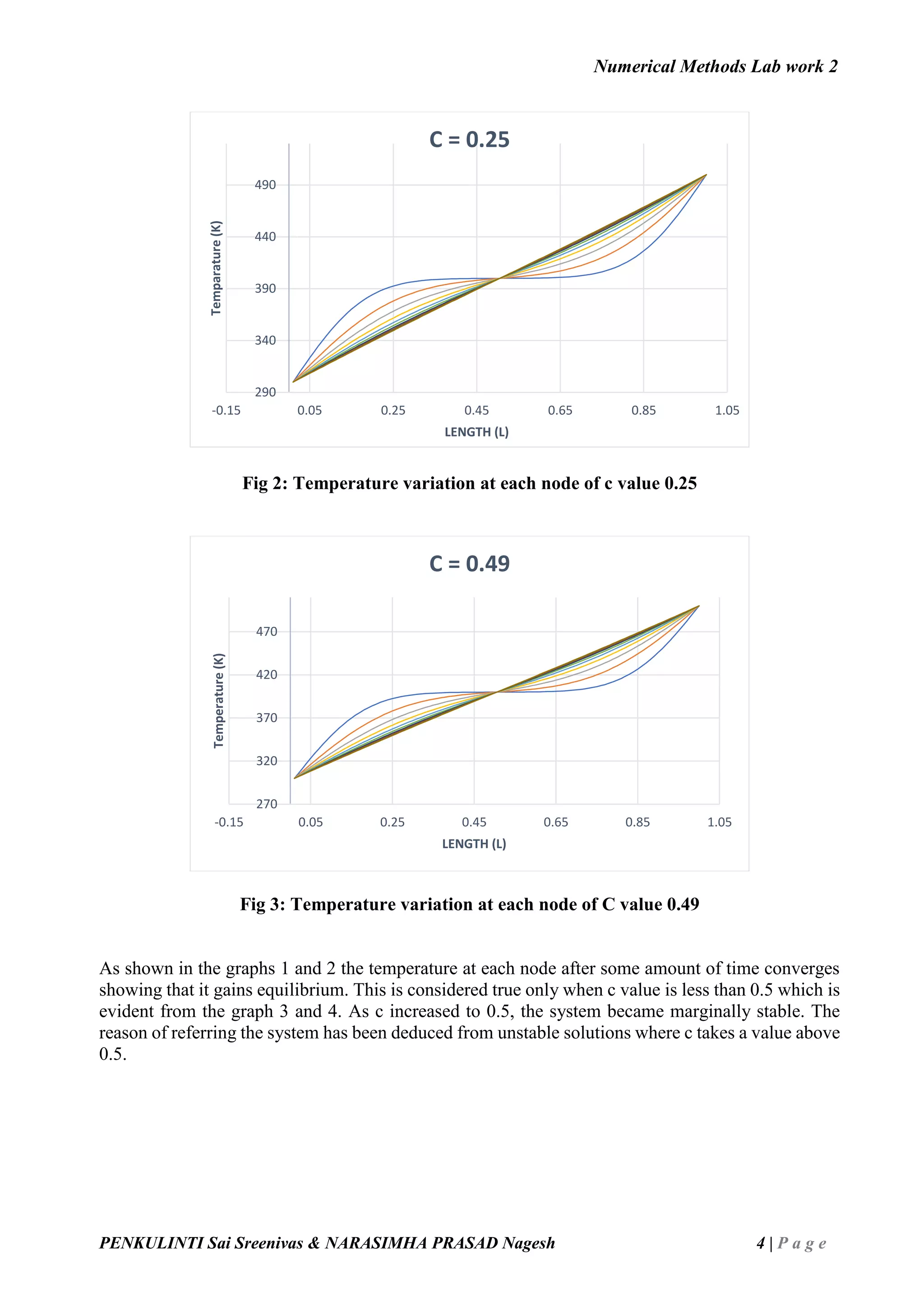
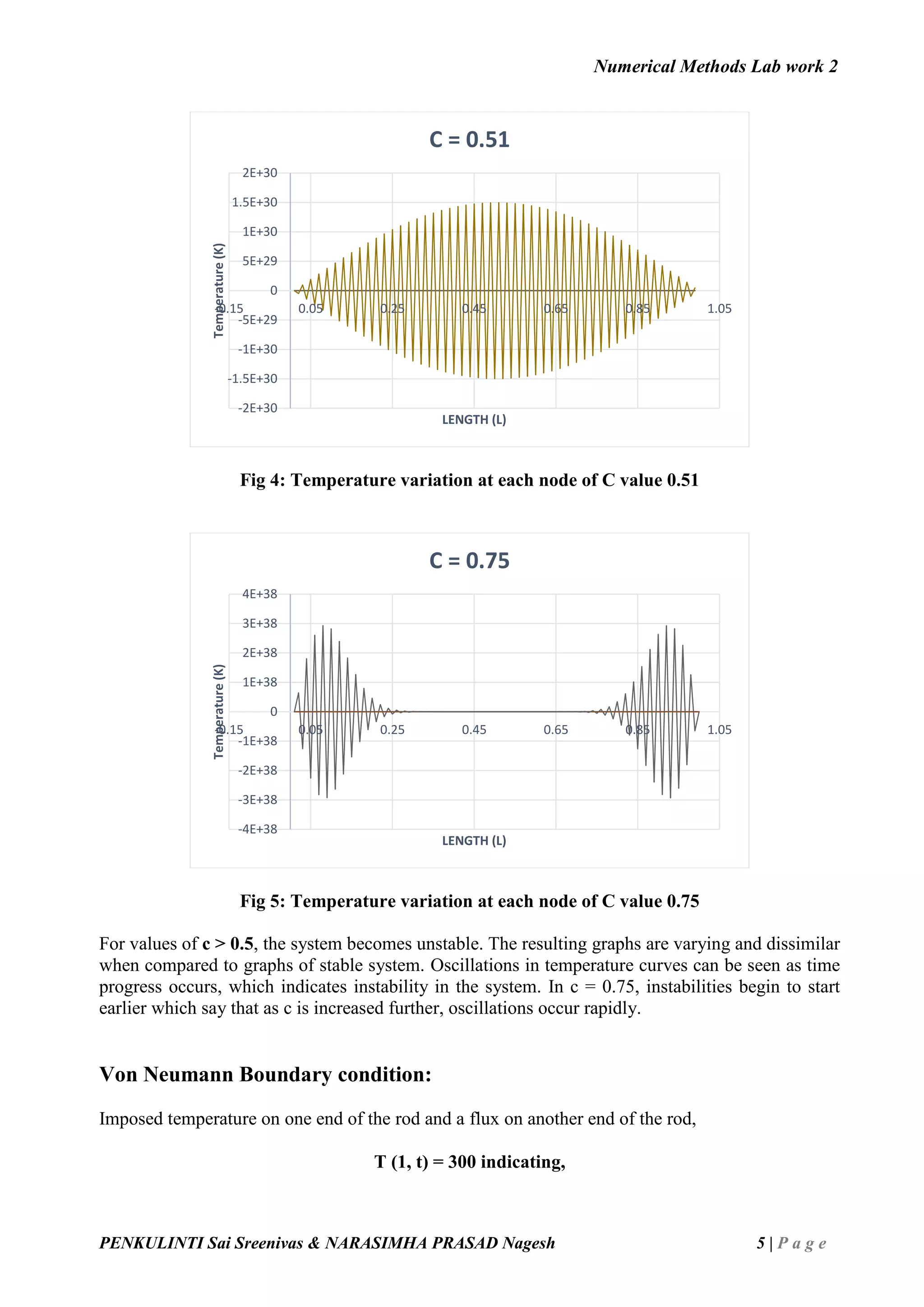
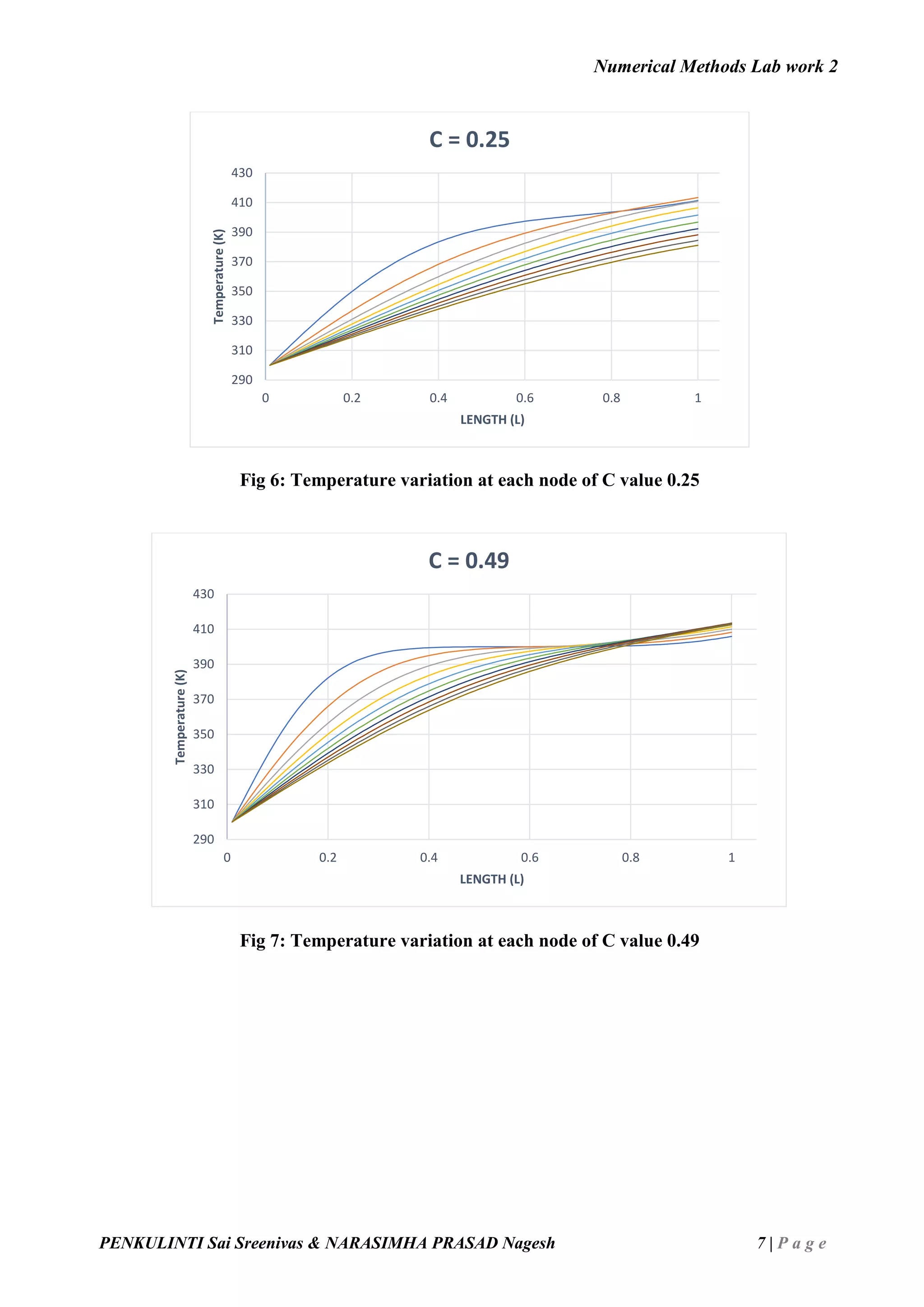
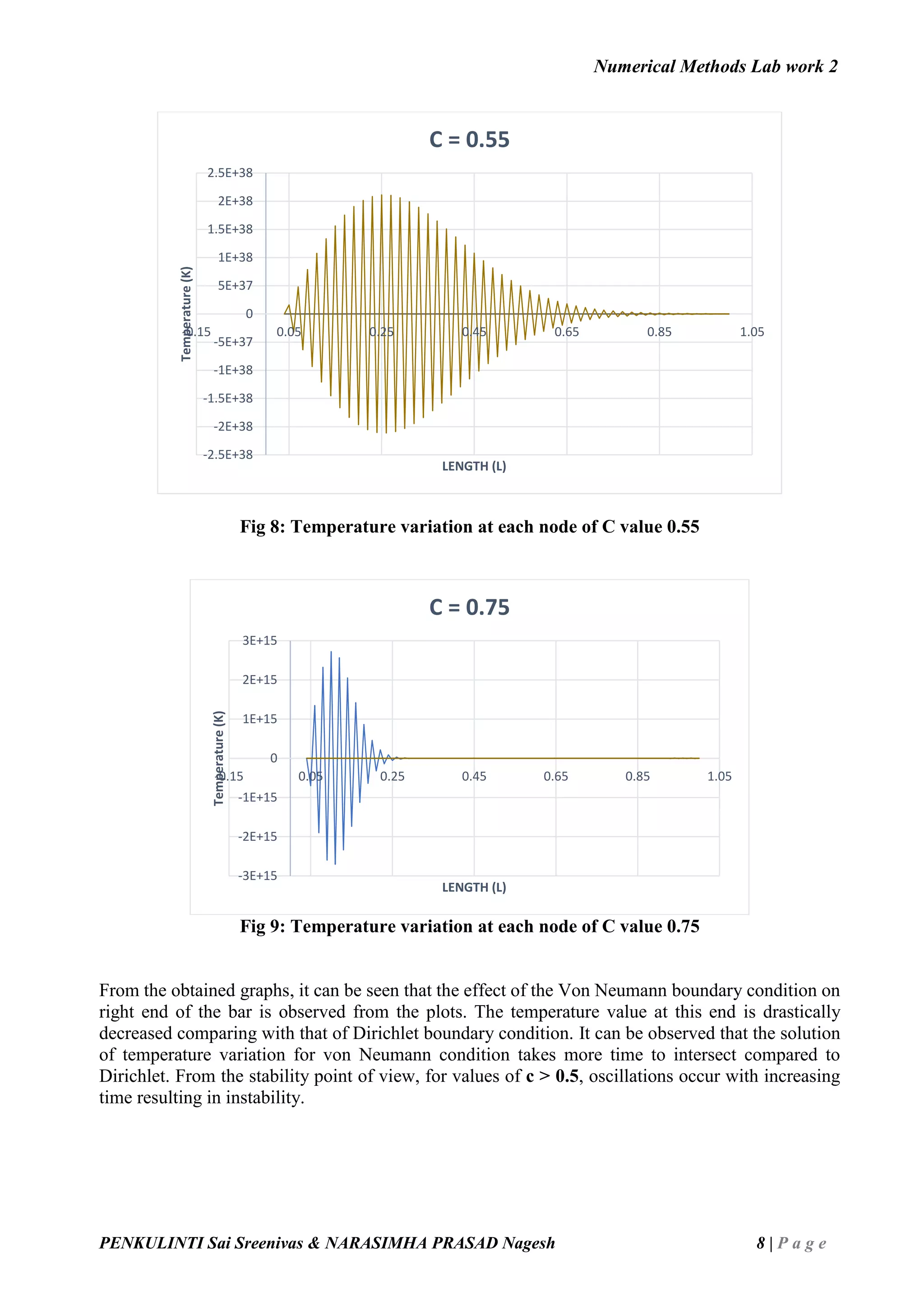
14. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 10 | P a g e
The equation for the last but one nod can be written as,
𝑇 𝑁−1
𝑘
= −𝑐𝑇 𝑁−1
𝑘+1
+ (1 + 2𝑐)𝑇 𝑁
𝑘+1
− 𝑐𝑇 𝑁+1
𝑘+1
This temperature is maintained at all times for this problem. The initial condition is same as the
previous one given by T(x, 1) = 400 indicating,
𝑇𝑗
1
= 400
Applying the boundary conditions in the obtained equation with j varying from 2 to N-1
𝑇𝑗
𝑘
= −𝑐𝑇𝑗−1
𝑘+1
+ (1 + 2𝑐)𝑇𝑗
𝑘+1
− 𝑐𝑇𝑗+1
𝑘+1
Writing the system of equation in the matrix form
𝐴. 𝑇 𝑘+1
= 𝑇 𝑘
+ 𝐵
[
1 + 2𝑐 −𝑐 0
−𝑐 ⋱ ⋱
0 ⋱ 1 + 2𝑐
] (
𝑇1
𝑘+1
⋮
𝑇 𝑁
𝑘+1
) = (
𝑇1
𝑘
⋮
𝑇 𝑁
𝑘
) + [
300
⋮
500
]
Where A is tridiagonal matrix with 1+2c as the main diagonal and -c as the lower and upper diagonal.
B is the boundary condition matrix with only two entries at the extreme nodes and the other values
being 0.

15. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 11 | P a g e
CONCLUSION
Altogether in this lab work we used finite difference method to solve a heat equation and apply the
same to a rod which is heated from one end. Here application of two different boundary conditions
is done viz. Dirichlet and Von Neumann through which we solve the given problem. This task helped
in understanding application of FDM on heat equation analysis and also made us familiarize with
different boundary conditions. The implicit mode of solving is done analytically by which we obtain
the matrix form of the given problem as written in the report. In order to execute the program for
implicit it is required to make use of DGESV function which is not submitted in this lab work. We
tried programming the code where we got few errors which we were unable to rectify.

16. Numerical Methods Lab work 2
PENKULINTI Sai Sreenivas & NARASIMHA PRASAD Nagesh 12 | P a g e
REFERENCES
1. Team CODE::BLOCKS, http://www.codeblocks.org/downloads/26
Version 17.12, Dated 30 Dec 2017.
2. Tutorials Point – Fortran Tutorials, https://www.tutorialspoint.com/fortran/index.htm
3. Stanford education - Learn Fortran, https://web.stanford.edu/class/me200c/tutorial_90/
4. Moodle ENSMA – Numerical Methods Links, https://moodle.ensma.fr/course/
5. https://en.wikipedia.org/wiki/Talk%3ANeumann_boundary_condition for Vonn Neumann
condition.
6. https://en.wikipedia.org/wiki/Nondimensionalization for non dimensionalization.