Embed presentation
Downloaded 2,498 times



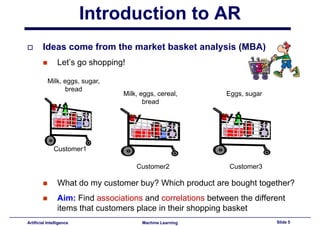

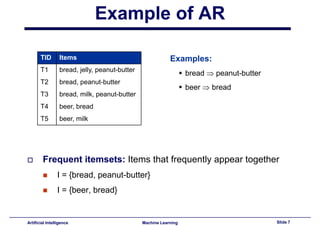


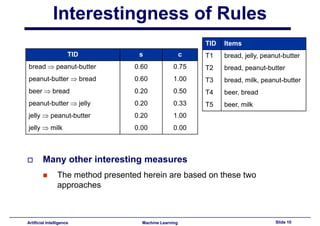


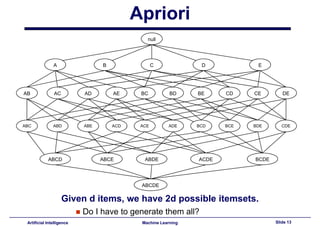

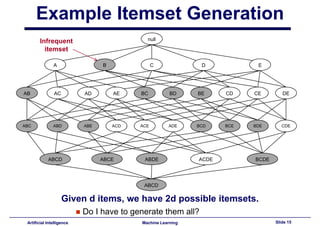
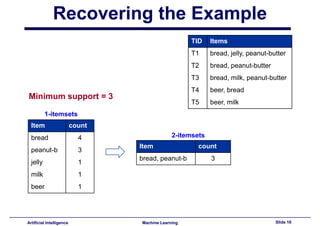



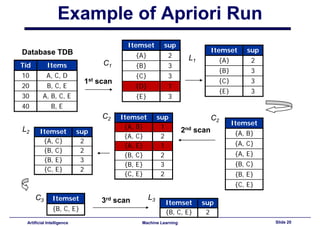



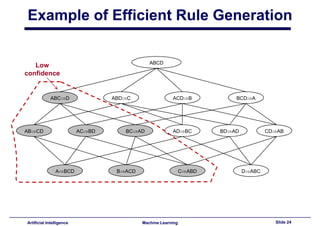



This document provides an introduction to association rule mining. It begins with an overview of association rule mining and its application to market basket analysis. It then discusses key concepts like support, confidence and interestingness of rules. The document introduces the Apriori algorithm for mining association rules, which works in two steps: 1) generating frequent itemsets and 2) generating rules from frequent itemsets. It provides examples of how Apriori works and discusses challenges in association rule mining like multiple database scans and candidate generation.


























