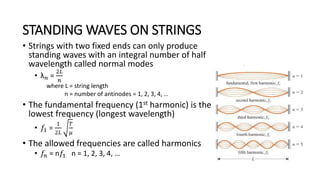
This document discusses standing waves on violin strings. It explains that standing waves are stationary waves formed by the superposition of two harmonic waves moving in opposite directions. Standing waves can be generated when a string is plucked with both ends fixed. The string will form nodes at points of zero amplitude and antinodes at points of maximum amplitude. For a string with two fixed ends, only certain integral multiples of half wavelengths are allowed as normal modes of vibration. The fundamental frequency of the string depends on the string length, tension, and linear mass density.

1. STANDING WAVES
ON
VIOLIN STRINGS

2. STANDING WAVES
• Are stationary (as opposed to travelling waves)
• Vs
STANDING WAVE TRAVELLING WAVE

3. STANDING WAVES
• Are the superposition of two
harmonic waves with equal
amplitude, frequency and
wavelengths but moving in
opposite direction
v
v
Resulting Standing Wave
from adding the two
harmonic waves

4. STANDING WAVES
• Can be generated by plucking a string with
both ends fixed
• Nodes are points with zero amplitudes
• Antinodes are points with maximum
amplitudes

5. STANDING WAVES ON STRINGS
• Strings with two fixed ends can only produce
standing waves with an integral number of half
wavelength called normal modes
• λ 𝑛 =
2𝐿
𝑛
where L = string length
n = number of antinodes = 1, 2, 3, 4, …
• The fundamental frequency (1st harmonic) is the
lowest frequency (longest wavelength)
• 𝑓1 =
1
2𝐿
𝑇
𝜇
where T = tension in the string
𝜇 = linear mass density of the string =
𝑚𝑎𝑠𝑠 𝑜𝑓 𝑠𝑡𝑟𝑖𝑛𝑔
𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑠𝑡𝑟𝑖𝑛𝑔
• The allowed frequencies are called harmonics
• 𝑓𝑛 = n𝑓1 n = 1, 2, 3, 4, …

6. QUESTION PART 1
Tom wants to make a violin for his sister as a birthday present.
Violins usually make sound frequencies ranging from
200~3000Hz. He has a few 30 cm long strings with linear mass
densities:
A 2.8 × 10−4
kg/m
B 4.0 × 10−4
kg/m
C 0.62 g/m
Which string should he use to make the violin in order to get a
fundamental frequency of 700Hz if the tension in the string is
kept at 70 N?

7. Hints
• What variables are given in the question?
• The fundamental frequency (𝑓1), tension (T), and string length (L)

8. Hints
• What variables are given in the question?
• The fundamental frequency (𝑓1), tension (T), and string length (L)
• Which equation to use when solving for linear mass density?
• 𝑓1 =
1
2𝐿
𝑇
𝜇
where T = tension in the string
𝜇 = linear mass density of the string =
𝑚𝑎𝑠𝑠 𝑜𝑓 𝑠𝑡𝑟𝑖𝑛𝑔
𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑠𝑡𝑟𝑖𝑛𝑔

9. Solution — Tom should use string B
𝑓1 = 700 Hz T = 70 N L = 30 cm = 0.30 m
𝑓1 =
1
2𝐿
𝑇
𝜇
Solve for 𝜇
𝑓1 × 2𝐿 =
𝑇
𝜇
(𝑓1 × 2𝐿) 2
=
𝑇
𝜇
𝜇 =
𝑇
( 𝑓1×2𝐿)
2 =
70 𝑁
(700 𝐻𝑧×2×0.30𝑚)
2 = 3.97× 10−4 kg/ m
≈ 4.0 × 10−4
kg/m

10. QUESTION PART 2
The violin string broke after a few weeks, but Tom
doesn’t have anymore of the same string. If he
uses a string with linear mass density of 4.7 ×
10−4
kg/m, what should the tension be in the
string in order to produce the same sound
frequency (700 Hz)?

11. Hints
• What variables are given in the question?
• The fundamental frequency (𝑓1), linear mass density (𝜇),
and string length (L)

12. Hints
• What variables are given in the question?
• The fundamental frequency (𝑓1), linear mass density (𝜇),
and string length (L)
• Which equation to use when solving for tension?
• 𝑓1 =
1
2𝐿
𝑇
𝜇
where T = tension in the string
𝜇 = linear mass density of the string =
𝑚𝑎𝑠𝑠 𝑜𝑓 𝑠𝑡𝑟𝑖𝑛𝑔
𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑠𝑡𝑟𝑖𝑛𝑔

13. Solution
𝑓1 = 700 Hz 𝜇 = 4.7 × 10−4
kg/m L = 30 cm = 0.30 m
𝑓1 =
1
2𝐿
𝑇
𝜇
Solve for T
𝑓1 × 2𝐿 =
𝑇
𝜇
(𝑓1 × 2𝐿) 2
=
𝑇
𝜇
T = (𝑓1 × 2𝐿) 2
× 𝜇 = (700𝐻𝑧 × 2 × 0.30𝑚) 2
× 4.7 × 10−4
kg/m
= 82.9 N
≈ 83 N

14. THANK YOU FOR WATCHING