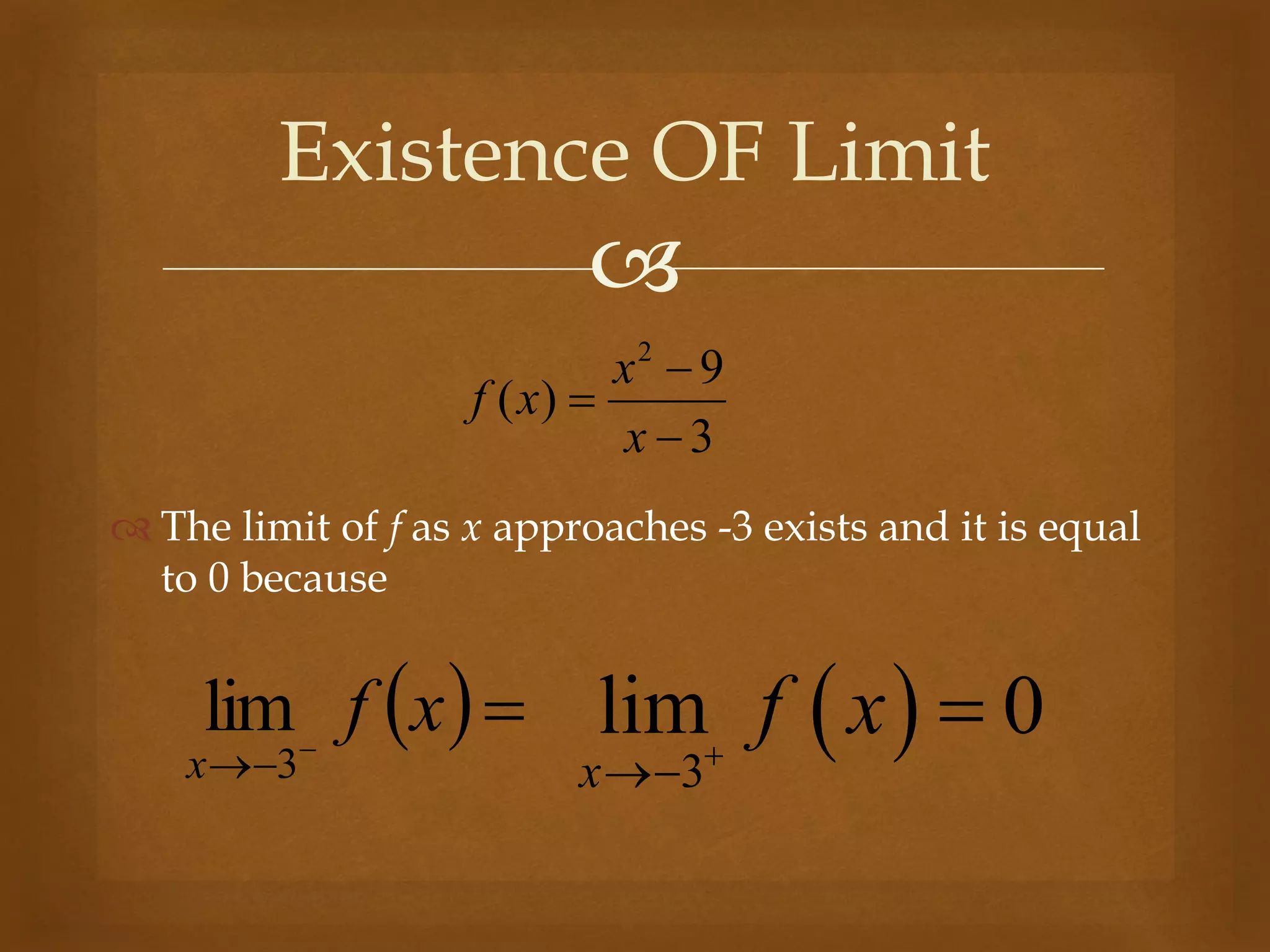Embed presentation
Downloaded 159 times





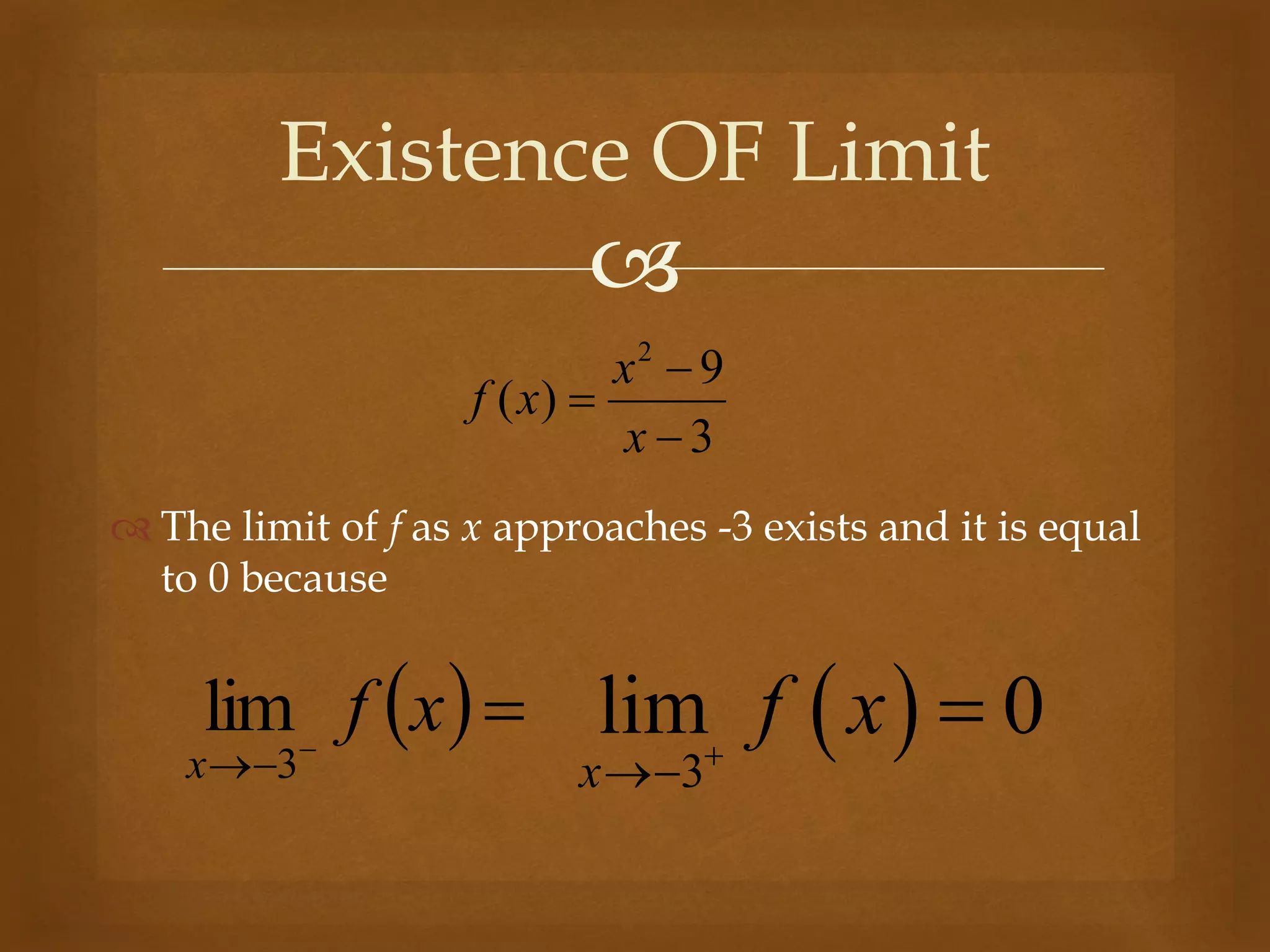









The document discusses different types of limits in calculus and analysis. A limit describes the behavior of a function near a particular input value. There are several types of limits including one-sided limits as x approaches a from the left or right, direct substitution limits where the value is simply substituted, and limits involving techniques like factoring, rationalization, as x approaches infinity, trigonometric functions, or the number e.