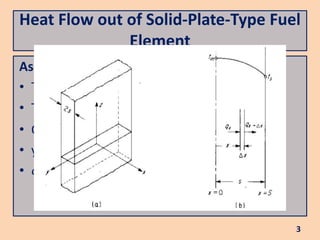
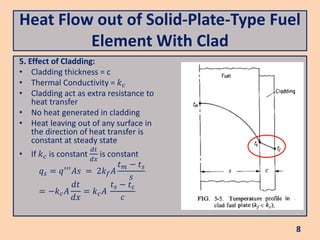
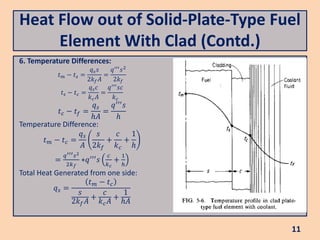
The document discusses heat flow in a solid-plate-type fuel element, detailing the methods to derive the Poisson equation for heat conduction and temperature distribution. It explains the effects of thermal conductivity, boundary conditions, and the impact of cladding on heat transfer. Additionally, it covers the heat transfer from the fuel element to coolant and the resulting temperature differences.

1. • 𝑡𝑚 − 𝑡𝑠 =
𝑞′′′𝑅2
4𝑘𝑓
• 𝑞(𝑟) = 𝜋𝑟2
𝐿𝑞′′′
• 𝑞𝑠 = 𝜋𝑅2𝐿𝑞′′′
• 𝑞𝑠 = 4𝜋𝑘𝑓𝐿(𝑡𝑚 − 𝑡𝑠)
• Therefore: 𝑞𝑠 = 2𝑘𝑓𝐴𝑠
𝑡𝑚−𝑡𝑠
𝑅
1

2. Syed Muhammad Haris
Chapter 5
Lecture 2

3. Heat Flow out of Solid-Plate-Type Fuel
Element
Assumptions:
• Thin, Bare and Plate-type fuel element
• Thermal Conductivity 𝑘𝑓
• Cross-Sectional Area = Constant
• y and z dimension → infinity
• 𝜙 𝑎𝑛𝑑 𝑞′′′
= Constant
3

4. Heat Flow out of Solid-Plate-Type Fuel
Element (Contd.)
1 (a) First Method to Get Poisson Equation:
– General Heat Conduction Equation:
𝛻2𝑡 +
𝑞′′′
𝑘
=
1
𝛼
𝜕𝑡
𝜕𝜃
– Poisson Equation:
𝛻2𝑡 +
𝑞′′′
𝑘
= 0
– For one-dimension i.e. x-dimension
𝑑2
𝑡
𝑑𝑥2
+
𝑞′′′
𝑘
= 0
4

5. Heat Flow out of Solid-Plate-Type Fuel
Element (Contd.)
1 (b) Second Method to Get Poisson
Equation:
– Applying Heat Balance:
𝐻𝑒𝑎𝑡 𝐶𝑟𝑜𝑠𝑠𝑖𝑛𝑔
𝑃𝑙𝑎𝑛𝑒 𝑥 + Δ𝑥
=
𝐻𝑒𝑎𝑡 𝐶𝑟𝑜𝑠𝑠𝑖𝑛𝑔
𝑃𝑙𝑎𝑛𝑒 𝑥
+
𝐻𝑒𝑎𝑡 𝐺𝑒𝑛𝑒𝑟𝑎𝑡𝑒𝑑
𝑖𝑛 𝐿𝑎𝑦𝑒𝑟
𝑞𝑥+Δ𝑥 = 𝑞𝑥 + 𝑞′′′
𝐴Δ𝑥
𝑞′′′𝐴Δ𝑥 = −𝑘𝑓𝐴
𝑑2𝑡
𝑑𝑥2
Δ𝑥
𝑑2𝑡
𝑑𝑥2
+
𝑞′′′
𝑘
= 0
5

6. Heat Flow out of Solid-Plate-Type Fuel
Element (Contd.)
2. Integration to get
temperature
distribution:
𝑑2𝑡
𝑑𝑥2
= −
𝑞′′′
𝑘
=
𝑞′′′𝑅2
𝑘𝑓
𝑡 = −
𝑞′′′
2𝑘𝑓
𝑥2
+ 𝐶1𝑥 + 𝐶2
6
3. Boundary Conditions:
𝑑𝑡
𝑑𝑥
= 0 𝑎𝑡 𝑥 = 0
𝑡 = 𝑡𝑚 𝑎𝑡 𝑥 = 0
𝑑𝑡(𝑥)
𝑑𝑥
= −
𝑞′′′
𝑘𝑓
𝑥
𝑡(𝑥) = −
𝑞′′′
2𝑘𝑓
𝑥2 + 𝑡𝑚
Surface Temperature:
𝑡 = 𝑡𝑠 𝑎𝑡 𝑥 = 𝑠
𝑡𝑠 = 𝑡𝑚 −
𝑞′′′
2𝑘𝑓
𝑠2

7. Heat Flow out of Solid-Plate-Type Fuel
Element (Contd.)
4. Heat Conducted out
from a plane
Between x=0 and x:
𝑞𝑠 = 𝐿𝑞′′′
𝑟2
Total Heat Generated from
one side (x=s):
𝑞𝑠 = 𝑞′′′
𝐴𝑠
As: 𝑡𝑠 = 𝑡𝑚 −
𝑞′′′
2𝑘𝑓
𝑠2
⇒ 𝑞′′′ = 2𝑘𝑓
𝑡𝑚 − 𝑡𝑠
𝑠2
7
Total Heat Generated
from both sides (As =
2𝐴):
𝑞𝑠 = 2𝑘𝑓𝐴𝑠
𝑡𝑚 − 𝑡𝑠
𝑠

8. Heat Flow out of Solid-Plate-Type Fuel
Element With Clad
5. Effect of Cladding:
• Cladding thickness = c
• Thermal Conductivity = 𝑘𝑐
• Cladding act as extra resistance to
heat transfer
• No heat generated in cladding
• Heat leaving out of any surface in
the direction of heat transfer is
constant at steady state
• If 𝑘𝑐 is constant
𝑑𝑡
𝑑𝑥
is constant
𝑞𝑠 = 𝑞′′′𝐴𝑠 = 2𝑘𝑓𝐴
𝑡𝑚 − 𝑡𝑠
𝑠
= −𝑘𝑐𝐴
𝑑𝑡
𝑑𝑥
= 𝑘𝑐𝐴
𝑡𝑠 − 𝑡𝑐
𝑐
8

9. Heat Flow out of Solid-Plate-Type Fuel
Element With Clad (Contd.)
6. Temperature Differences:
𝑡𝑚 − 𝑡𝑠 =
𝑞𝑠𝑠
2𝑘𝑓𝐴
=
𝑞′′′
𝑠2
2𝑘𝑓
𝑡𝑠 − 𝑡𝑐 =
𝑞𝑠𝑐
𝑘𝑐𝐴
=
𝑞′′′
𝑠𝑐
𝑘𝑐
Temperature Difference:
𝑡𝑚 − 𝑡𝑐 =
𝑞𝑠
𝐴
𝑠
2𝑘𝑓
+
𝑐
𝑘𝑐
=
𝑞′′′𝑠2
2𝑘𝑓
+
𝑞′′′𝑠𝑐
𝑘𝑐
Total Heat Generated from one side:
𝑞𝑠 =
𝐴 𝑡𝑚 − 𝑡𝑐
𝑠
2𝑘𝑓
+
𝑐
𝑘𝑐
Total Heat Generated from both sides:
𝑞2𝑠 =
𝐴𝑠 𝑡𝑚 − 𝑡𝑐
𝑠
2𝑘𝑓
+
𝑐
𝑘𝑐
9

10. Heat Flow out of Solid-Plate-Type Fuel
Element With Clad and Coolant
7. Heat transfer form Fuel Element to
Coolant:
• Bulk Coolant Temperature = 𝑡𝑓
• Heat Transfer Coefficient= h
• No heat generated in cladding and
coolant
• Heat leaving out of any surface in
the direction of heat transfer is
constant at steady state
• If 𝑘𝑐 is constant
𝑑𝑡
𝑑𝑥
is constant
𝑞𝑠 = 𝑞′′′𝐴𝑠 = 2𝑘𝑓𝐴
𝑡𝑚 − 𝑡𝑠
𝑠
= −𝑘𝑐𝐴
𝑑𝑡
𝑑𝑥
= 𝑘𝑐𝐴
𝑡𝑠 − 𝑡𝑐
𝑐
= ℎ𝐴(𝑡𝑐 − 𝑡𝑓)
10

11. Heat Flow out of Solid-Plate-Type Fuel
Element With Clad (Contd.)
6. Temperature Differences:
𝑡𝑚 − 𝑡𝑠 =
𝑞𝑠𝑠
2𝑘𝑓𝐴
=
𝑞′′′
𝑠2
2𝑘𝑓
𝑡𝑠 − 𝑡𝑐 =
𝑞𝑠𝑐
𝑘𝑐𝐴
=
𝑞′′′
𝑠𝑐
𝑘𝑐
𝑡𝑐 − 𝑡𝑓 =
𝑞𝑠
ℎ𝐴
=
𝑞′′′
𝑠
ℎ
Temperature Difference:
𝑡𝑚 − 𝑡𝑐 =
𝑞𝑠
𝐴
𝑠
2𝑘𝑓
+
𝑐
𝑘𝑐
+
1
ℎ
=
𝑞′′′𝑠2
2𝑘𝑓
+𝑞′′′
𝑠
𝑐
𝑘𝑐
+
1
ℎ
Total Heat Generated from one side:
𝑞𝑠 =
𝑡𝑚 − 𝑡𝑐
𝑠
2𝑘𝑓𝐴
+
𝑐
𝑘𝑐𝐴
+
1
ℎ𝐴
11