Download to read offline
More Related Content
Similar to G9-Science-Q2-Week-1-Quantum.pptxppycppt
G9-Science-Q2-Week-1-Quantum.pptxppycppt
- 1. Quantum Theory and theAtom ELECTRONS IN ATOMS AND THE PERIODIC TABLE PREPARED BY: TYPE YOUR NAME HERE
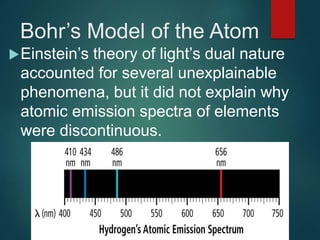
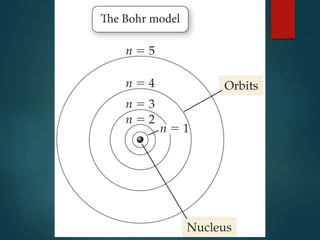
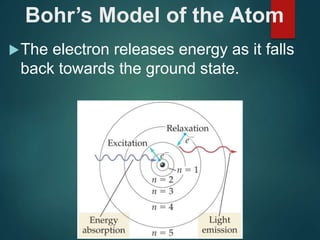
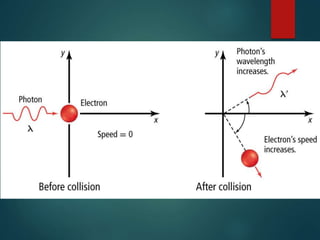
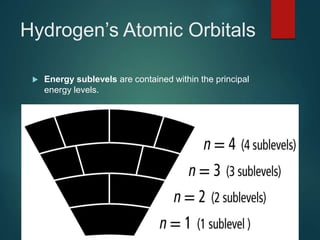
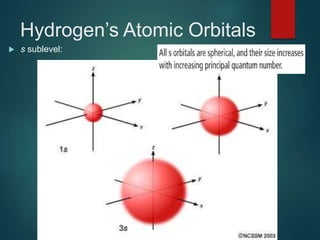
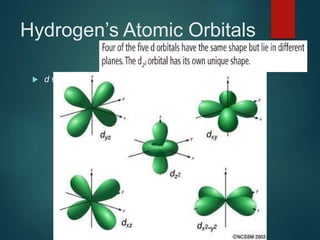
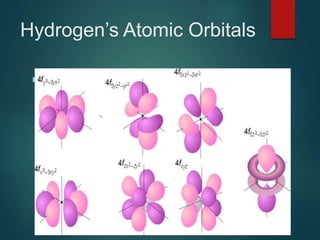
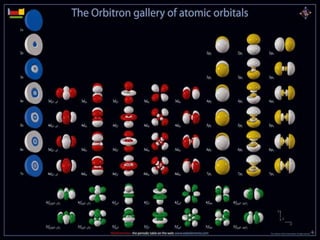
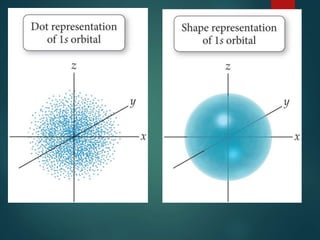
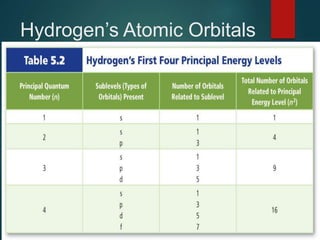
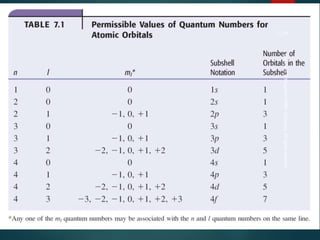
- 2. LEARNING OBJECTIVE Explainhow the Quantum Mechanical Model of the atom describes the energies and positions of the electrons
- 3. Learning Goals Comparethe Bohr and quantum mechanical models of the atom. Explain the impact of de Broglie’s wave particle duality and the Heisenberg uncertainty principle on the current view of electrons in atoms. Identify the relationships among a hydrogen atom’s energy levels, sublevels, and atomic orbitals.
- 4. Bohr’s Model ofthe Atom Einstein’s theory of light’s dual nature accounted for several unexplainable phenomena, but it did not explain why atomic emission spectra of elements were discontinuous.
- 5. Bohr’s Model ofthe Atom In 1913, Niels Bohr, a Danish physicist working in Rutherford’s laboratory, proposed a quantum model for the hydrogen atom that seemed to answer this question.
- 7. Bohr’s Model ofthe Atom The lowest allowable energy state of an atom is called its ground state. When an atom gains energy, it is in an excited state.
- 8. Bohr’s Model ofthe Atom Bohr suggested that an electron moves around the nucleus only in certain allowed circular orbits.
- 9. Bohr’s Model ofthe Atom Each orbit was given a number, called the quantum number. Bohr orbits are like steps of a ladder, each at a specific distance from the nucleus and each at a specific energy.
- 10. Bohr’s Model ofthe Atom Hydrogen’s single electron is in the n = 1 orbit when it is in the ground state. When energy is added, the electron moves to the n = 2 orbit.
- 11. Bohr’s Model ofthe Atom The electron releases energy as it falls back towards the ground state.
- 12. Bohr’s Model ofthe Atom Bohr’s model explained the hydrogen’s spectral lines, but failed to explain any other element’s lines. For this and other reasons, the Bohr model was replaced with a more sophisticated model called the quantum-mechanical or wave- mechanical model.
- 13. Quantum Mechanical Model Louisde Broglie (1892–1987) hypothesized that particles, including electrons, could also have wavelike behaviors. Electrons do not behave like particles flying through space. We cannot, in general, describe their exact paths.
- 14. Quantum Mechanical Model Heisenbergshowed it is impossible to take any measurement of an object without disturbing it. The Heisenberg uncertainty principle states that it is fundamentally impossible to know precisely both the velocity and position of a particle at the same time.
- 16. Quantum Mechanical Model The onlyquantity that can be known is the probability for an electron to occupy a certain region around the nucleus.
- 17. Quantum Mechanical Model Schrödingertreated electrons as waves in a model called the quantum mechanical model of the atom. Schrödinger’s equation applied equally well to elements other than hydrogen (unlike Bohr’s model).
- 18. Quantum Mechanical Model Orbitals aredifferent from orbits in that they represent probability maps that show a statistical distribution of where the electron is likely to be found.
- 19. Quantum Mechanical Model Inthe quantum-mechanical model, a number and a letter specify an orbital. The lowest-energy orbital is called the 1s orbital. It is specified by the number 1 and the letter s.
- 20. Hydrogen’s Atomic Orbitals Thenumber is called the Principal quantum number (n) and it indicates the relative size and energy of atomic orbitals. n specifies the atom’s major energy levels, called the principal energy levels.
- 21. Hydrogen’s Atomic Orbitals Energy sublevels are contained within the principal energy levels.
- 22. Hydrogen’s Atomic Orbitals Each energy sublevel relates to orbitals of different shape. s s, p s, p, d s, p, d, f
- 23. Hydrogen’s Atomic Orbitals s sublevel:
- 24. Hydrogen’s Atomic Orbitals p sublevel:
- 25. Hydrogen’s Atomic Orbitals d sublevel:
- 26. Hydrogen’s Atomic Orbitals f sublevel:
- 28. Hydrogen’s Atomic Orbitals Orbitals are sometimes represented by dots, where the dot density is proportional to the probability of finding the electron. The dot density for the 1s orbital is greatest near the nucleus and decreases farther away from the nucleus. The electron is more likely to be found close to the nucleus than far away from it.
- 30.
- 31. Hydrogen’s Atomic Orbitals At any given time, hydrogen’s electron can occupy just one orbital. When hydrogen is in the ground state, the electron occupies the 1s orbital. When the atom gains a quantum of energy, the electron is excited to one of the unoccupied orbitals.
- 32. Quantum Numbers Aset of quantum numbers gives an information about the atomic orbital where an electrons may be found A. principal B. Azimuthal C. Magnetic D. Spin
- 33. A. Principal quantumnumber (n) - indicates the energy level n= 1,2,3,4 …. B. Azimutham Quantum Number (ℓ) - specifies the sublevel or subshell ℓ= 0 to n-1
- 34. c. Magnetic quantumnumber (mℓ) - indicates the specific orbital within the sublevel where the electron is found -ℓ to +ℓ Example: n=1, ℓ = 0 , mℓ = 0 n =2, ℓ = 0,1 , mℓ = 0, -1, 0, +1
- 35. D. Spin quantumNumber - according to Pauli Exclusion Principle, only a maximum of two electrons can occupy an orbital, and they must have opposite spins to minimize repulsion between them. + ½ or - ½
- 36.
- 37. 1.What are thepossible sets of quantum numbers that can describe a 2p electron in an atom? 2. Give the set of quantum numbers for each of the six electrons that occupy the 4p orbitals
- 38. 3.Give the electronconfiguration of Li. Give the set of quantum numbers that describe the outermost electron in lithium as shown in the orbital diagram below. 4. Give the set of quantum numbers of Cr
- 39. Determine the elementwhose outermost valence electron is represented by the following quantum numbers. a. n=1, l= 0, ml= 0, ms=-1/2 b. n=2, l=1, ml= 0, ms= +1/2 c. n=3, l=1, ml= 0, ms= +1/2 d. n=4, l=2, ml= 0, ms= +1/2 e. n= 6, l=0, ml= 0, ms= -1/2
- 40. Which of thefollowing are permissible sets of quantum numbers? n = 4, l = 4, ml = 0, ms = ½ n = 3, l = 2, ml = 1, ms = -½ n = 2, l = 0, ml = 0, ms = ³/² n = 5, l = 3, ml = -3, ms = ½ 7 | 40
- 41. Content, images,text, etc. used belong to the rightful owner. No copyright infringement intended.