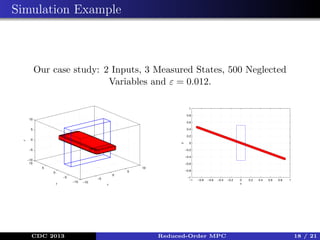
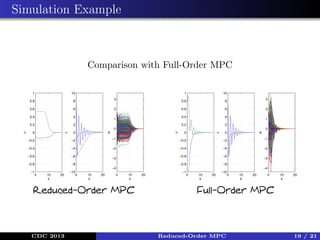
This document presents a method for model predictive control (MPC) using reduced-order models. Many physical systems are modeled using partial differential equations with thousands of states, making MPC computationally challenging. The method reduces the model order by treating some states as disturbances and estimating their bounds. An invariance result shows the error remains bounded. The MPC optimization problem is formulated subject to the reduced constraints. Simulation results show the reduced-order MPC matches full-order MPC performance while being significantly faster to compute.

1. Constrained Model Predictive Control Based on
Reduced-Order Models
Pantelis Sopasakis, Daniele Bernardini, and
Alberto Bemporad
IMT Institute for Advanced Studies Lucca
December 13, 2013
52nd IEEE Conf. Decision & Control,
Florence, Italy, 2013.
CDC 2013
Reduced-Order MPC
1 / 21

2. Model Reduction: Motivation
Challenge:
A lot of systems are modelled
with (∞-dimensional) PDEs
and whose approximations comprise tens of thousands of states.
MPC faces its limitations as the
state dimension goes into such
orders of magnitude.
CDC 2013
Reduced-Order MPC
2 / 21

3. Model Reduction: Motivation
Examples:
1. Sloshing of liquids (Ardakani & Bridges, 2011)
2. Distribution of anti-tumour drugs (Jackson & Byrne, 2000)
3. HVAC systems (Moukalled et al., 2011)
4. Seismic excitation of buildings (Banerji & Samanta, 2011)
5. Control of Flexible Structures (Rao et al., 1990)
CDC 2013
Reduced-Order MPC
3 / 21

4. Model Reduction
Consider a linear time-invariant control system in the form:
xk+1 = A11 xk + A12 wk + B1 uk
wk+1 = A21 xk + A22 wk + B2 uk ,
where:
1. xk ∈ Rnx is the measured (dominant) state,
2. wk ∈ Rnw is the unmeasured (neglected) state
Assumption 1. The pair (A11 , B1 ) is stabilizable and K is stabilizing gain for it.
CDC 2013
Reduced-Order MPC
4 / 21

5. Model Reduction
We impose the following state and input constraints:
xk ∈ X , uk ∈ U, ∀k ∈ N,
and we assume that we have some information about the position
of the initial value of the neglected variables:
w0 ∈ W
{w ∈ Rnw |w W −1 w ≤ 1}.
Assumption 2 (Reduced Model). There exists an ε ∈ (0, 1) so
that A22 W ⊆ εW (can be written as ε2 W − A22 W A22 0).
CDC 2013
Reduced-Order MPC
5 / 21

6. The Nominal System
We consider the following nominal system:
zk+1 = A11 zk + B1 vk ,
with zk ∈ Rnx , v ∈ Rnu . Define AK
and apply the feedback
uk =
vk
A11 + B1 K and e
+
MPC control action
Kek
x−z
.
Error feedback
The error dynamics is given by:
ek+1 = AK ek + A12 wk
Stable
CDC 2013
Disturbance
Reduced-Order MPC
6 / 21

7. An Invariance Result
Define the set
ˆ(∞)
SK
T1 W ⊕ T2 X ⊕ T3 U,
where
T1
T2
CDC 2013
T1 (I − A22 )−1 A21
T3
Reduced-Order MPC architecture.
(I − AK )−1 A12
T1 (I − A22 )−1 B2 .
If xk ∈ X , uk ∈ U for all k ∈ N
ˆ(∞)
ˆ(∞)
and e0 ∈ SK , then ek ∈ SK
for all k ∈ N.
Reduced-Order MPC
7 / 21

8. Ellipsoid+Polytope=?
Notice that:
ˆ(∞)
SK
T1 W ⊕ T2 X ⊕ T3 U ,
Ellipsoid
Reduced-Order MPC architecture.
CDC 2013
Polytope
Solution: The polytope ΓB∞ ,
with Γ = (T1 W T1 )1/2 is a
minimum-volume outbounding
parallelotope for T1 W.
Reduced-Order MPC
8 / 21

9. The MPC formulation
Let us introduce the sets
Z
X
ˆ(∞)
SK
V
U
ˆ(∞)
K SK ,
Along the prediction horizon N we impose the constraints:
zk ∈ Z, ∀k ∈ N[1,N −1]
vk ∈ V, ∀k ∈ N[0,N −1]
and the terminal constraint
zN ∈ Zf .
CDC 2013
Reduced-Order MPC
9 / 21

10. The MPC optimization problem is:
PN (z) : VN (z) = min VN (z, v),
v∈V(z)
where the cost function is given by:
N −1
VN (z, v)
zN P zN +
zk QzK + vk Rvk ,
k=0
and V(z) is the following multi-valued mapping:

z0 =z,



z =A11 zk +B1 vk , ∀k∈N[1,N −1] ,
V(z)
v k+1
zk ∈ Z, ∀k∈N[1,N −1] ,



vk ∈ V, ∀k∈N[0,N −1] , zN ∈ Zf
CDC 2013
Reduced-Order MPC




.



10 / 21

11. Exponential Robust Stability
Let κN be the MPC control action and
κN (z, x) = K(x − z) + κN (z).
˜
ˆ(∞)
The set SK × {0} is exponentially stable for the system
xk+1 = A11 xk + B1 (˜ N (zk , xk )) + A12 wk
κ
zk+1 = A11 zk + B1 κN (zk ),
(with state variable [ x ]) over the domain of attraction
z
(∞)
ˆ
(ZN ⊕ SK ) × ZN .
CDC 2013
Reduced-Order MPC
11 / 21

12. Can we do better?
1. The estimation wk ∈ W for all k ∈ N can be very
conservative for k = 0,
2. Online measurements of xk and uk can be used to estimate
the whereabouts of wk+i|k by sets Wk+i|k – then:
j
Ai A12 Wk+i|k .
K
ek+j|k ∈ Sk+j|k =
i=0
3. All online operations must be carried out in low
dimensional spaces.
CDC 2013
Reduced-Order MPC
12 / 21

13. Set Membership Estimator
A set membership estimator for wk consists of a correction and
a prediction step concisely written as:
Wk−1|k =
w ∈ Wk−1|k−1 |A12 w=xk −A11 xk−1 −B1 uk−1
Wk|k = A21 xk−1 + B2 uk−1 ⊕ A22 Wk−1|k ,
while along the prediction horizon we have:
Wk+j|k = A21 Xk+j−1|k ⊕ B2 U ⊕ A22 Wk+j−1|k ,
where
Xk+j|k = X ∩ (A11 Xk+j−1|k ⊕ B1 U ⊕ A12 Wk+j−1|k ).
CDC 2013
Reduced-Order MPC
13 / 21

14. Lightweight Set Membership Estimator
We compute sets Hk+j|k so that
hk+j|k
A12 wk ∈ Hk+j|k ,
with
H0|0 = A12 W0|0
¯
W0|0 = W ←
Polytopic
Overapprox. of W.
The set membership estimator is given by:
k−1
Hk|k =
A12 Ak W
22
A2 (A21 xj + B2 uj )
22
⊕ A12
j=0
k−1
¯
⊆ εk A12 W ⊕ A12
T (xj , uj , εj )B∞
j=0
CDC 2013
Reduced-Order MPC
14 / 21

15. Lightweight Set Membership Estimator
Along the prediction horizon we have:
Hk+j|k = A12 A21 Xk+j−1|k ⊕A12 B2 U⊕εHk+j−1|k ,
Xk+j|k = X ∩ (A11 Xk+j−1|k ⊕ Hk+j−1|k ⊕ B1 U).
The error is then bound in
j
Ai Hk+i|k
K
Sk+j|k =
i=0
CDC 2013
Reduced-Order MPC
15 / 21

16. Model Predictive Control
The MPC problem becomes...
VN (zk , Hk|k ) =
min
¯
v∈V(zk ,Hk|k )
VN (zk , v),
where the set of constraints encompasses:
zk+j|k ∈ Zk+j|k X Sk+j|k
Vk+j|k U
KSk+j|k
Reduced-Order MPC
architecture in presence of a
set-membership estimator.
CDC 2013
Reduced-Order MPC
16 / 21

17. Exponential Robust Stability
Stability Result:
Assume that Hk|k → H and let S
(I − AK )−1 H . The set
S × {0}
is exponentially stable for the dynamics of [ x ].
z
Reduced-Order MPC
architecture in presence of a
set-membership estimator.
CDC 2013
Reduced-Order MPC
17 / 21

18. Simulation Example
Our case study: 2 Inputs, 3 Measured States, 500 Neglected
Variables and ε = 0.012.
1
0.8
10
0.6
0.4
5
y
z
0.2
0
−5
0
−0.2
−0.4
−10
10
−0.6
5
10
5
0
−5
y
CDC 2013
−0.8
0
−1
−1
−5
−10
−10
−0.8
−0.6
−0.4
x
Reduced-Order MPC
−0.2
0
x
0.2
0.4
0.6
0.8
1
18 / 21

19. Simulation Example
Comparison with Full-Order MPC
1
10
0.8
8
0.6
6
0.4
4
0.2
2
0
1
0
6
0.4
4
0.2
1
8
0.6
2
10
0.8
3
2
0
0
3
2
1
−0.2
−4
−0.6
−6
−0.8
−8
−0.2
−4
−0.6
−6
−0.8
−3
−1
−2
−0.4
−2
w
x
u
−1
−2
−0.4
0
w
x
u
0
−8
−2
−3
−4
−1
−4
−10
0
10
k
20
−1
0
10
k
20
0
10
k
Reduced-Order MPC
CDC 2013
20
−10
0
10
k
20
0
10
k
20
0
10
k
20
Full-Order MPC
Reduced-Order MPC
19 / 21

20. Simulation Example
Reduced-Order MPC is of course way faster...
Table : Computational times
Reduced-Order
MPC
Computation of P , K, Z, V, Zf
Solution of the MPC problem (avg.)
Solution of the MPC problem (st. dev)
CDC 2013
Full-Order
MPC
1.3s
8.4ms
±0.42ms
14.4s
14297ms
±859ms
Reduced-Order MPC
20 / 21

21. Thank you for your attention!
CDC 2013
Reduced-Order MPC
21 / 21

22. References
1. H. A. Ardakani and T. J. Bridges, “Shallow-water sloshing in vessels
undergoing prescribed rigid-body motion in three dimensions,” J.
Fluid Mechanics, vol. 667, pp. 474519, 2011.
2. T. L. Jackson and H. M. Byrne, “A mathematical model to study the
effects of drug resistance and vasculature on the response of solid
tumors to chemotherapy,” Math. Biosc., vol. 164, no. 1, pp. 17 38,
2000.
3. F. Moukalled, S. Verma, and M. Darwish, “The use of CFD for
predicting and optimizing the performance of air conditioning
equipment,” Int. J. Heat and Mass Transfer, vol. 54, no. 13, pp. 549
563, 2011.
4. P. Banerji and A. Samanta, “Earthquake vibration control of
structures using hybrid mass liquid damper,” Engineering Structures,
vol. 33, no. 4, pp. 1291 1301, 2011.
CDC 2013
Reduced-Order MPC
21 / 21

23. References
5. S. Rao, T. Pan, and V. Venkayya, “Modeling, control, and design of
flexible structures: A survey,” Appl. Mech. Rev., vol. 43, no. 5, 1990.
6. T.Bui-Thanh,K.Willcox,O.Ghattas,andB.vanBloemenWaanders,
Goal-oriented, model-constrained optimization for reduction of largescale systems, Journal of Computational Physics, vol. 224, no. 2, pp.
880 896, 2007.
7. T. L. Jackson and H. M. Byrne, “A mathematical model to study the
effects of drug resistance and vasculature on the response of solid
tumors to chemotherapy,” Math. Biosc., vol. 164, no. 1, pp. 17 38,
2000.
CDC 2013
Reduced-Order MPC
21 / 21