The document presents a comprehensive study on fast parallelizable scenario-based stochastic optimization, focusing on stochastic optimal control problems, their formulations, and solution methods. It includes discussions about the forward-backward line-search algorithm, dual gradient algorithms, and Hessian-vector product computations, showcasing their implementations and results using NVIDIA GPUs. The work aims to enhance computational efficiency in solving complex optimization problems across various applications.

1. Fast parallelizable scenario-based stochastic
optimization
Ajay K. Sampathirao∗, Pantelis Sopasakis∗,
Alberto Bemporad∗, Panos Patrinos∗∗
∗ IMT School for Advanced Studies Lucca, Italy,
∗∗ ESAT, KU Leuven, Belgium.
September 14, 2016

2. I. Stochastic Optimal Control

3. Stochastic Optimal Control
Optimisation problem:
V (p) = min
π={uk}k=N−1
k=0
E Vf (xN , ξN ) +
N−1
k=0
k(xk, uk, ξk) ,
s.t x0 = p,
xk+1 = Aξk
xk + Bξk
uk + wξk
,
Sampathirao et al., 2015, 2016.

4. Stochastic Optimal Control
Optimisation problem:
V (p) = min
π={uk}k=N−1
k=0
E Vf (xN , ξN ) +
N−1
k=0
k(xk, uk, ξk) ,
s.t x0 = p,
xk+1 = Aξk
xk + Bξk
uk + wξk
,
where:
At time k we measure xk and ξk−1
Sampathirao et al., 2015, 2016.

5. Stochastic Optimal Control
Optimisation problem:
V (p) = min
π={uk}k=N−1
k=0
E Vf (xN , ξN ) +
N−1
k=0
k(xk, uk, ξk) ,
s.t x0 = p,
xk+1 = Aξk
xk + Bξk
uk + wξk
,
where:
At time k we measure xk and ξk−1
E[·]: conditional expectation wrt the product probability measure
Sampathirao et al., 2015, 2016.

6. Stochastic Optimal Control
Optimisation problem:
V (p) = min
π={uk}k=N−1
k=0
E Vf (xN , ξN ) +
N−1
k=0
k(xk, uk, ξk) ,
s.t x0 = p,
xk+1 = Aξk
xk + Bξk
uk + wξk
,
where:
At time k we measure xk and ξk−1
E[·]: conditional expectation wrt the product probability measure
Casual policy uk = ψk(p,ξξξk−1), with ξξξk = (ξ0, ξ1, . . . , ξk)
Sampathirao et al., 2015, 2016.

7. Stochastic Optimal Control
Optimisation problem:
V (p) = min
π={uk}k=N−1
k=0
E Vf (xN , ξN ) +
N−1
k=0
k(xk, uk, ξk) ,
s.t x0 = p,
xk+1 = Aξk
xk + Bξk
uk + wξk
,
where:
At time k we measure xk and ξk−1
E[·]: conditional expectation wrt the product probability measure
Casual policy uk = ψk(p,ξξξk−1), with ξξξk = (ξ0, ξ1, . . . , ξk)
and Vf can encode constraints
Sampathirao et al., 2015, 2016.

8. Splitting of k
The stage cost is a function k : IRn
× IRm
× Ωk → ¯IR
k(xk, uk, ξk) = φk(xk, uk, ξk) + ¯φk(Fkxk + Gkuk, ξk),
where φ is real-valued, convex, smooth, e.g.,
φk(xk, uk, ξk) = xkQξk
xk + ukRξk
uk,
and ¯φ is proper, convex, lsc, and possibly non-smooth, e.g.,
¯φk(xk, uk, ξk) = δ(Fkxk + Gkuk | Yξk
).

9. Scenario tree

10. Splitting
We have
f(x)=
N−1
k=0
µk
i=1
pi
kφ(xi
k,ui
k,i) +
µN
i=1
pi
N φN (xi
N , i)+δ(x|X(p)),
g(Hx)=
N−1
k=0
µk
i=1
pi
k
¯φ(Fi
kxi
k+Gi
kui
k,i)+
µN
i=1
pi
N
¯φN (Fi
N xi
N , i),
where
X(p) = {x : xj
k+1 = Aj
kxi
k + Bj
kui
k + wj
k, j ∈ child(k, i)}

11. Dual optimization problem
For the primal problem
minimize f(x) + g(Hx),
its Fenchel dual is
minimize f∗
(−H y)
f◦(y)
+ g∗
(y)
g◦(y)
.
We need to be able to compute
1. proxγg◦
(Moreau decomposition)
2. f◦(y) (Conjugate subgradient theorem)
3. Products of the form 2f◦(y) · d
Under very weak assumptions, strong duality holds.

12. II. The Forward-Backward
Line-Search Algorithm

13. Problem statement
minimize ϕ(x) := f(x) + g(x)
f, g closed proper convex
f : IRn
→ IR is L-smooth
f(z) ≤ Qf
1/L(z; x) := f(x) + f(x), z − x + L
2 z − x 2
, ∀x, z
g : IRn
→ IR ∪ {+∞} has easily computable proximal mapping
proxγg(x) = arg min
z∈IRn
g(z) + 1
2γ z − x 2
Parikh & Boyd, 2014.

14. Forward-Backward Splitting (FBS)
xk+1
= arg min
z
Qf
γ(z; xk
) + g(z)
x0
ϕ(x0)
ϕ = f + g

15. Forward-Backward Splitting (FBS)
xk+1
= arg min
z
Qf
γ(z; xk
) + g(z)
x0
ϕ(x0)
ϕ = f + g

16. Forward-Backward Splitting (FBS)
xk+1
= arg min
z
Qf
γ(z; xk
) + g(z)
x0
ϕ(x0)
ϕ = f + g
Qf
γ(z; x0
) + g(z)

17. Forward-Backward Splitting (FBS)
xk+1
= arg min
z
Qf
γ(z; xk
) + g(z)
x0 x1
ϕ(x0)
ϕ(x1)
ϕ = f + g
Qf
γ(z; x0
) + g(z)

18. Forward-Backward Splitting (FBS)
xk+1
= arg min
z
Qf
γ(z; xk
) + g(z)
x0 x1 x2
ϕ(x0)
ϕ(x1)
ϕ(x2)
ϕ = f + g
Qf
γ(z; x1
) + g(z)

19. Forward-Backward Splitting (FBS)
xk+1
= arg min
z
Qf
γ(z; xk
) + g(z)
x0 x1 x2 x3
ϕ(x0)
ϕ(x1)
ϕ(x2)
ϕ(x3)
ϕ = f + g
Qf
γ(z; x2
) + g(z)

20. Forward-Backward Splitting (FBS)
The basic FBS algorithm is
xk+1 = proxγg(xk − γ f(xk))
which is a fixed point iteration for
x = proxγg(x − γ f(x)).

21. Forward Backward Envelope
ϕγ(x) = min
z
f(x) + f(x), z − x + 1
2γ z − x 2
+ g(z)
x
ϕ(x)
ϕγ(x)
ϕ
Stella et al., 2016 arXiv:1604.08096; Patrinos and Bemporad, 2013.

22. Forward Backward Envelope
ϕγ(x) = min
z
f(x) + f(x), z − x + 1
2γ z − x 2
+ g(z)
x
ϕ(x)
ϕγ(x)
ϕ
Stella et al., 2016 arXiv:1604.08096; Patrinos and Bemporad, 2013.

23. Forward Backward Envelope
ϕγ(x) = min
z
f(x) + f(x), z − x + 1
2γ z − x 2
+ g(z)
x
ϕ(x)
ϕγ(x)
ϕ
ϕγ
Stella et al., 2016 arXiv:1604.08096; Patrinos and Bemporad, 2013.

24. Forward Backward Envelope
Key property. The FBE ϕγ is always real-valued and
inf ϕ = inf ϕγ
arg min ϕ = arg min ϕγ
Minimizing ϕ becomes equivalent to solving an unconstrained optimization
problem. If f ∈ C2 then ϕγ ∈ C1 and
ϕγ(x) = (I − γ 2
f(x))Rγ(x),
so, arg min ϕγ = zer ϕγ.
Stella et al., 2016.

25. LBFGS on FBE
Algorithm 1 Forward-Backward L-BFGS
1: choose γ ∈ (0, 1/L), x0, m (memory), (tolerance)
2: Initialize an LBFGS buffer with memory m
3: while Rγ(xk) > do
4: dk ← −Bk ϕγ(xν) (Using the LBFGS buffer)
5: xk+1 ← xk + τkdk, τk: satisfies Wolfe conditions
6: sk ← xk+1 − xk, qk ← ϕγ(xk+1) − ϕγ(xk), ρk ← sk, qk
7: if ρk > 0 then
8: Push (sk, qk, ρk) into the LBFGS buffer

26. Global LBFGS
Algorithm 2 Global Forward-Backward L-BFGS
1: choose γ ∈ (0, 1/L), x0, m (memory), (tolerance)
2: Initialize an LBFGS buffer with memory m
3: while Rγ(xk) > do
4: dk ← −Bk ϕγ(xν) (Using the LBFGS buffer)
5: wk ← xk + τkdk, so that ϕγ(wk) ≤ ϕγ(xk)
6: xk+1 ← proxγg(wk − γ f(wk))
7: sk ← xk+1 − xk, qk ← ϕγ(xk+1) − ϕγ(xk), ρk ← sk, qk
8: if ρk > 0 then
9: Push (sk, qk, ρk) into the LBFGS buffer
Stella et al., 2016.

27. Global LBFGS
Any direction dk can be used (LBFGS, nonlinear CG, etc)
Adaptive version: when L is not known
ϕ(xk) converges to ϕ as O(1/k)∗
Linear convergece if ϕ is strongly convex
In practice it is very fast
∗
Provided ϕ has bounded level sets; Stella et al., 2016.

28. Stochastic optimal control
The dual gradient, fo(y), is computed using the conjugate subgradient
theorem
fo(y) = H arg min
z
{ z, H y + f(z)},
which is an unconstrained problem and can be solved with a Ricatti-type
recursion.

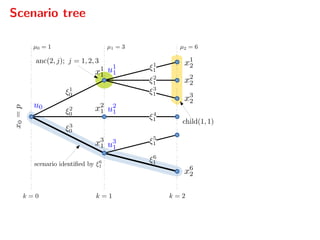
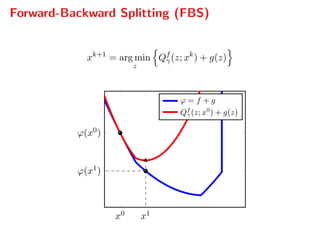
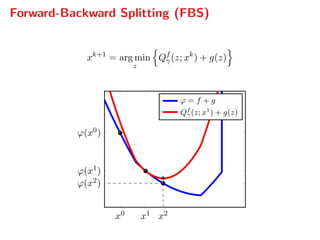
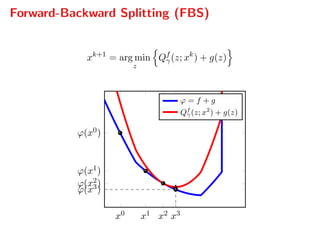
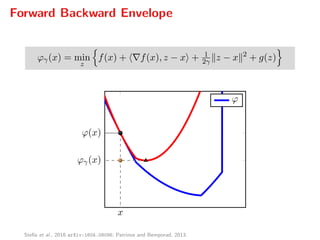
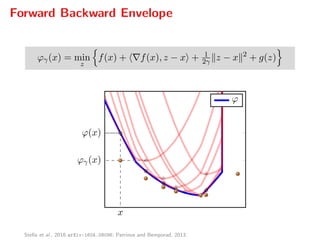
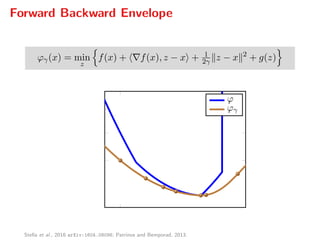
29. Dual gradient
Algorithm 3 Dual gradient computation
Input: y, Factorization matrices
Output: x∗ = {xi
k, ui
k}, so that f◦(y) = Hx∗
1: qi
N ← yi
N , ∀i ∈ N[1,µN ], x1
0 ← p
2: for k = N − 1, . . . , 0 do
3: for i = 1, . . . , µk do in parallel
4: ui
k ← Φi
kyi
k + j∈child(k,i) Θj
kqj
k+1 + σi
k matvec only
5: qi
k ← Di
k yi
k + j∈child(k,i) Λj
k qj
k+1 + ci
k
6: for k = 0, . . . , N − 1 do
7: for i = 1, . . . , µk do in parallel
8: ui
k ← Ki
kxi
k + ui
k
9: for j ∈ child(k, i) do in parallel
10: xj
k+1 ← Aj
kxi
k + Bj
kui
k + wj
k

30. Hessian-vector products
Algorithm 4 Computation of Hessian-vector products
Input: Vector d
Output: {ˆxi
k, ˆui
k} = 2f◦(y)d
1: ˆqi
N ← di
N , ∀i ∈ N[1,µN ], ˆx1
0 ← 0
2: for k = N − 1, . . . , 0 do
3: for i = 1, . . . , µk do in parallel
4: ˆui
k ← Φi
kdi
k + j∈child(k,i) Θj
k ˆqj
k+1 matvec only
5: ˆqi
k ← Di
k di
k + j∈child(k,i) Λj
k ˆqj
k+1
6: for k = 0, . . . , N − 1 do
7: for i = 1, . . . , µk do in parallel
8: ui
k ← Ki
k ˆxi
k + ˆui
k
9: for j ∈ child(k, i) do in parallel
10: ˆxj
k+1 ← Aj
k ˆxi
k + Bj
k ˆui
k

31. III. Results

32. Implementation
Implementation on NVIDIA Tesla 2075
Mass-spring system
10 states, 20 inputs, N = 15
Binary scenario tree

33. Convergence speed
50 100 150 200 250 300 350
Iterations
10 -3
10 -2
10 -1
10 0
Rλ
Dual APG
LBFGS FBE
LBFGS FBE (Global)

34. Runtimes (average)
6 8 10 12 14
log
2
(scenarios)
10 -2
10 -1
10 0
10 1
10 2
runtime(s)
LBFGS (Global)
APG
Gurobi

35. Runtimes (max)
6 8 10 12 14
log
2
(scenarios)
0
10
20
30
40
50
60
runtime(s)
LBFGS (Global)
APG

36. Iterations
6 8 10 12 14
0
100
200
iterations
Average
Maximum
6 8 10 12 14
log 2
(scenarios)
0
500
1000
iterations

37. References
1. A.K. Sampathirao, P. Sopasakis, A. Bemporad and P. Patrinos, “Proximal
quasi-Newton methods for scenario-based stochastic optimal control,” IFAC 2017,
submitted.
2. A.K. Sampathirao, P. Sopasakis, A. Bemporad and P. Patrinos, “Stochastic
predictive control of drinking water networks: large-scale optimisation and GPUs,”
IEEE CST (prov. accepted), arXiv:1604.01074
3. A.K. Sampathirao, P. Sopasakis, A. Bemporad and P. Patrinos, “Distributed
solution of stochastic optimal control problems on GPUs,” in Proc. 54th IEEE
Conf. on Decision and Control, Osaka, Japan, 2015, pp. 7183–7188.
4. L. Stella, A. Themelis and P. Patrinos, “Forward-backward quasi-Newton methods
for nonsmooth optimization problems,” arXiv:1604.08096, 2016.
5. P. Patrinos and A. Bemporad, “Proximal Newton methods for convex composite
optimization,” IEEE CDC 2013.
6. N. Parikh and S. Boyd, “Proximal Algorithms,” Foundations and Trends in
Optimization, 1(3), pp. 123–231, 2014.
7. J. Nocedal and S. Wright, “Numerical Optimization,” Springer, 2006.

38. Thank you for your attention.