This document provides information on determining sample sizes for research studies. It defines key terms like population, sample size, margin of error, and confidence level. It presents different formulas for calculating sample sizes based on whether the population is known or unknown, such as Yamane's formula, Cochran's formula, and formulas for case-control and cohort study designs. Examples are provided to demonstrate how to use the formulas to determine required sample sizes for various study scenarios and levels of confidence. References for further information on sampling techniques are also included.

1. Sample size determination
Miss Nazziwa Aisha
0705687875
aishanazziwa“@yahoo.ca
1

2. Sample size determination
2
 Sample size: refers to the number of
individuals included in a research study as a
representative of the total population.
 The sample size is determined from the target
study population.
 Sample size determination is the most crucial
methodological part of a research study.
 It is essential for an investigator to estimate
optimum sample size to produce reliable
results.

3. 3

4. Definition of Terms
4
 True Population value: The actual value of a
population parameter (e.g. prevalence).
 Margin of Error: amount of error you wish to allow
in your results.
 Confidence Level: It tells us how confident we are
that if a study was repeatedly done, we would get the
same results. Usually 90%, 95% & 99%.
 Standard Deviation: It tells us the variance in data
with reference to the mean of the sample.

5. Definition of Terms
5

6. Definition Cont’d
Z-value: this is in relation to the Confidence
level. It is got from the Z table as indicated
below;
6
Confidence Level Z-score
90% 1.645
95% 1.96
99% 2.58

7. LLM/IPSK/UCU/OIL & GAS----DAVID TIBAMANYA 7

8. Sample size determination Cont’d.
8
 From the study population and applying confidence
levels of 95% and a margin of error of 5%, the
sample size can be determined using
 Morgan and Krejcie table
 Formulae

9. Morgan and Krejcie Table
It is used when the population is known
9

10. Formulae
10
Yamane’s formula
It is used when population is known
n= N/(1+Ne2)
Where n= sample size
N=study population
E=error of margin
For a study whose confidence level is 95%, e=5%
90%, e=10% etc

11. Yamen’s formula-Example
11
Suppose we want to evaluate a program where
1000 medical doctors were encouraged to adopt a
new practice; i.e. if Confidence level is 95% and
margin of error +/- 5%
n= N/(1+Ne2)
n= 1000/1+1000*0.052
n= 1000/2.5
n=400

12. Cochran’s formula
It is used for unknown population
12
n= (z2pq)/e2
Where n=sample size
Z=considering a confidence level of 95%, the z-value is
read from the normal distribution table Z=1.96
p=estimate proportion of an attribute present in a given
population (for maximum sample size p is usually
50%= 0.5
q=1-p
e=error of margin=5% or 0.05

13. Cochran Formula-Example
Examples
A local health department wishes to estimate the prevalence of
tonsillitis among children under five years of age in its locality.
It is known that the true rate is unlikely to exceed 20%. The
department wants to estimate the prevalence to within 5
percentage points of the true value, with 95% confidence.
How many children should be included in the sample?
13

14. Cochran Formula-Example
Solution:
• Proportion (Prevalence of tonsillitis in the population)
=20%
• Confidence level CI=95% (i.e. Z1-α/2=1.96)
Absolute precision (15%-25%) 5 percentage points
• The sample size formula for estimating a population
proportion with a given absolute precision is:
14

15. Cochran Formula-Example
• Z 1-α/2 = CI (95%), => Z 1-α/2 =1.96.
• P=20% => P= 0.20
• q= (1-P) => q =1-0.20 Therefore q= 0.80
• d =5% => d = 0.05.
Substituting the values for each the formula, we get:
• n =
(1.96)2(0.20)(1−0.20)
(0.05)2
=> n =
(1.96𝑥1.96)(0.20)(0.80)
(0.05𝑥0.05)
n = 245.86 ≈ 246
Therefore, for P = 0.20, d = 0.05 a sample size of 246
would be needed.
15

16. Cochran Formula-cont..
Example 2:
A researcher wants to carry out a descriptive study to
understand the prevalence of diabetes mellitus among
adults in Kampala city. A previous study stated that
diabetes in the adult population was 40%. At 95% CI
and 5% margin of error, calculate the sample required
to conduct the new research?
=> n=
(1.96𝑥1.96)(0.40)(0.60)
(0.05𝑥0.05)
n=368.79
• n= 369+37 (considering 10% dropout of study participants)
NB: I.e. Z1-α/2 =1.96, P=40%=0.4, q=1-p, =>q =1-0.4 = 0.6, d = 5% = 0.05

17. ANALYTICAL STUDIES
(i) Sample Size Estimation for Case–control Studies:
Case – Control study is a study that determines the cause
and effect, to see if exposure is correlated with an
outcome (i.e. disease or condition of interest) or not.
Sample size, when proportion parameter of the study or
data are on nominal/ordinal scale:
17

18. Case Control studies cont….
n= Desired number of samples
r= Control to cases ratio (r=1 if same numbers of
subject in both groups)
Z1-β = It is the desired power (0.84 for 80% power and
1.28 for 90% power)
Z1-α/2 = Confidence Interval. (At 95% CI =1.96 or 5%
error and at 99% CI or 1% error CI=2.58) 18

19. Case Control studies cont….
P= Proportion of population P =
𝑃1+𝑃2
2
NB: P1 = Proportion in cases, P2 = Proportion in controls
Desired power Z1-β is the probability that the
researcher will not commit type II error during
analysis.
19

20. Example
A researcher wants to conduct a case–control design to
identify the link between deep vein thrombosis and
pulmonary embolism. He decides to work at 95% CI and
80% power of the study. He assumes expected
proportion in case is 40% and control group is 30% and
decides to have same number of cases in both groups.
Find out the optimum sample size for each group in
study.

21. 21
=> n =
(1+1)
1
x
0.35(1−0.35)(0.84+1.96)2
(0.40−0.30)2
(n) = 2*178.36 (n) = 356.72
(n) = 357+36 (considering 10% dropout of study participants) Sample size
(n) = 393
P1 = 40% = 0.4 P2 = 30% = 0.3 r = 1 Z1-β = 0.84
Z1-α/2 = 1.96 P = 0.4+0.3/2 = 0.35
The researcher have to take a minimum of 393 subjects
in case as well as in the control group

22. Same Size Estimation for Cohort Studies
22
Sample Size estimation for a Cohort study
n =
[𝑍1
−
𝛼
/
2
√{
1+1
𝑚
𝑃 1−𝑃 }+𝑍1
−
𝛽√ {𝑃0∗
1−𝑃0
𝑚
𝑃1(1−𝑃1) ]2
(𝑃0−𝑃1)2
n = Total number of desired study subjects (cases)
m = Number of subjects (control)/experimental subject
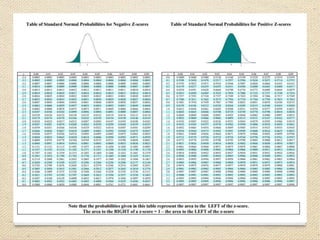
Z 1-β = desired power (0.84 for 80% P & 1.28 for 90% P)
Z1-α/2 = Critical value for level of confidence. (At 95% CI
=1.96 and at 99% CI or 1% CI= 2.58)

23. P0 = Possibility of event in controls
P1 = Possibility of event in experimental
p =
𝑃1+𝑚𝑃0
𝑀+1
Example:
A researcher wants to identify the impact of
smoking on lung cancer. A previous study stated that
proportion of lung cancer in the case group is 30%
and in the control group is 20%. Calculate the
sample size, if a researcher wishes to conduct the
study at 95% CI and 80% power with equal number
of case and control subjects.

24. n=
[1.96√{
1+1
1
0.25 1−0.25 }+0.84√ {0.2∗
1−0.2
1
0.3(1−0.3) ]2
(0.2−0.3)2
n =
[1.96√{ 2 0.25 0.75 }+0.84√ {0.2∗ 0.8 0.3(0.7) ]2
(0.2−0.3)2
n =
[1.96𝑥0.612+0.84𝑥0.1833 ]2
(−0.1)2
n =
[1.19952+0.153972 ]2
(0.01)
n =
1.83194
(0.01)
(n) = 183.17
(n) = 183+18 = 201 (considering 10% dropout rate)

25. 25

26. References
26
 Crochan, W.G. (1963). Sampling techniques, 2nd ed., Newyork: John Wiley
and Sons, Inc.
 Yamane, T. (1967). Statistics, An introductory analysis, 2nd ed., New York:
Harper and Row.
 Krejcie, R. V., & Morgan, D. W. (1970). Determining sample size for
research activities. Educational and psychological measurement, 30(3),
607-610.