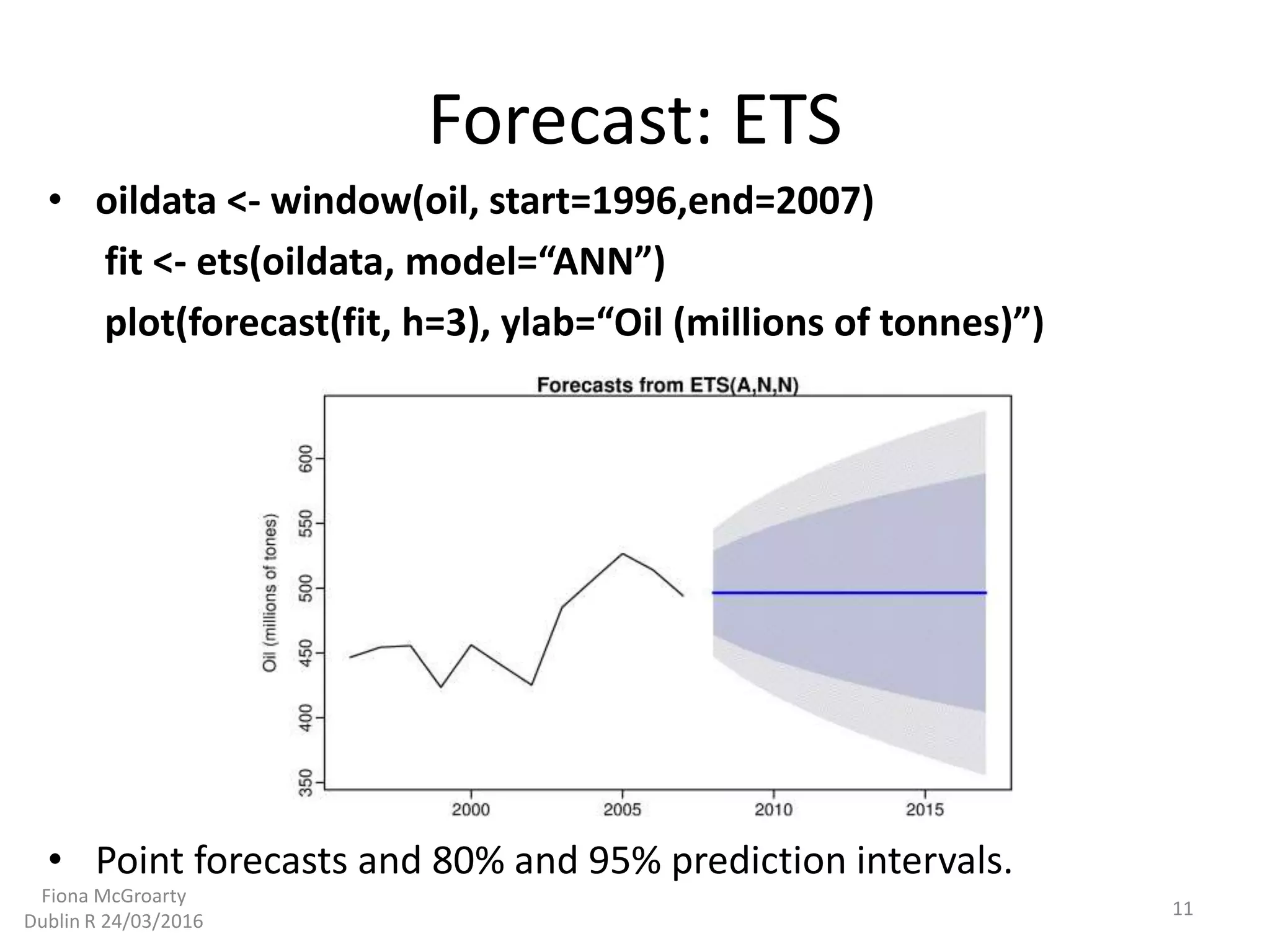
- The document discusses techniques for time series forecasting including exponential smoothing (ETS) and ARIMA models. It provides examples of using the forecast package in R to predict values based on historical time series data, decompose time series into seasonal, trend and error components, and select the best fitting ETS or ARIMA model. The goal is to predict things like wind speed or energy demand at various forecast horizons like hours or days ahead.

1. Time Series Analysis & fpp
• Used to predict wind speeds at forecast horizons of 10
minutes to 1 day ahead, based on historical wind speeds (10
minute averages).
• Forecast package: Rob Hyndman
• https://www.otexts.org/fpp - good explanations and worked
examples.
1
Fiona McGroarty
Dublin R 24/03/2016

2. Time Series Data
• Forecasting extrapolates trend and seasonal patterns.
• Trend : long term increased/decrease.
• Seasonal: e.g. daily
weekly, yearly (fixed
& known length).
• Cycle: rises/falls that
are not a fixed period
(variable & unknown
length).
Trend: Generally increasing
Seasonal Pattern: Sharp rise at the
end of each year (stockpiling)
• Observations (at regular intervals) sequentially over time.
2
Fiona McGroarty
Dublin R 24/03/2016

3. Autocorrelations
• Correlation: lags 4 & 8 –
seasonal pattern, peaks are
4 quarters apart.
• Linear relationship between
lagged values of a time series
(quarterly beer production):
Lag.plot(beer2, lags=9).
• Corr. Coefficient -1 ≤ r ≤ 1.
• Correlation: lags 2 & 6 –
troughs are 2 quarters
behind peaks.
3
Fiona McGroarty
Dublin R 24/03/2016

4. Autocorrelations
• Plot ACF (acf(beer2)):
• White Noise: 95% of spikes
are within ±2/T (T = length
of time series=50).
4
Fiona McGroarty
Dublin R 24/03/2016

5. Autocorrelations
• Plot ACF (acf(beer2)):
• White Noise: 95% of spikes
are within ±2/T (T = length
of time series=50).
5
Fiona McGroarty
Dublin R 24/03/2016

6. Simple Forecasts (Benchmarks)
• Naïve method: forecast = value of last observation:
naive(beer2, h=11) or rwf(beer2, h=11).
• Average method: forecast = mean of historical data:
meanf(beer2, h=11).
• Seasonal naïve: forecast = value of last observation from the
previous season
(month/quarter/year ...)
snaive(beer2, h=11).
6
Fiona McGroarty
Dublin R 24/03/2016

7. Simple Forecasts (Benchmarks)
• Drift: variation on naïve, allow forecast to increase/decrease
over time: rwf (dj2, h=42, drift=TRUE)
7
Fiona McGroarty
Dublin R 24/03/2016

8. Time Series Decomposition
• fit <- stl (elecequip,
t.window=15,
s.window=“periodic”,
robust=TRUE).
Plot(fit).
• Time series decomposition: yt = St + Tt + Et or yt = St × Tt × Et
Electrical equipment orders. (Seasonal, Trend, Error)
• Set trend window and seasonal
window sizes – small values
allow more rapid changes.
8
Fiona McGroarty
Dublin R 24/03/2016

9. Forecast: ETS
• Effects of components can be additive (A), multiplicative (M) or
ignored (N, none). EG ETS (MAN) forecasts by multiplying errors
(M), adding trends (A) and ignoring seasonal effects (N).
SES: Simple Exponential Smoothing
Holts Linear Method
Additive Holts-Winter Method
Multiplicative Holts-Winter Method
Holts-Winter damped method
• ETS (ANN) SES with + errors; ETS (MNN) SES with × errors.
• Some are numerically unstable e.g. if data contains 0 or neg. values.
• ETS(ZZZ) – runs all (stable) ETS models and returns the optimal one.
• ETS (Error, Trend, Seasonal OR ExponenTial Smoothing)
9
Fiona McGroarty
Dublin R 24/03/2016

10. EG: Forecasts using Holt’s method
10
Fiona McGroarty
Dublin R 24/03/2016

11. Forecast: ETS
• oildata <- window(oil, start=1996,end=2007)
fit <- ets(oildata, model=“ANN”)
plot(forecast(fit, h=3), ylab=“Oil (millions of tonnes)”)
• Point forecasts and 80% and 95% prediction intervals.
11
Fiona McGroarty
Dublin R 24/03/2016

12. ARIMA Models
• ARIMA (p, d, q) e.g. ARIMA101 model uses one past time-
lagged wind speed autocorrelation term (p = 1), is not
differentiated (d = 0) and uses one past forecast error (q = 1).
• ARIMA = Auto Regression (detects similarity in the data using
timelagged values of the variable) Integrated (the data may
have to be differentiated a number of times to make it
stationary) Moving Average (using weighted moving average
of the past few forecast errors).
• Can specify the ARIMA (p, d, q) model to use, or use
auto.arima
12
Fiona McGroarty
Dublin R 24/03/2016

13. ARIMA Models
• fit <- auto.arima (usconsumption[,1], seasonal=FALSE
plot(forecast(fit, h=10), include=80)
• Best ARIMA model is returned, in this case it’s ARIMA(0,0,3).
• fit <- Arima(usconsumption[,1], order=c(0,0,3))
13
Fiona McGroarty
Dublin R 24/03/2016

14. Lots of other things to consider….
• Stationarity of data
• Transforming data before forecasting – differentiating…
• Error Metrics! Calculate MAE, RMSE,…..
14
Fiona McGroarty
Dublin R 24/03/2016