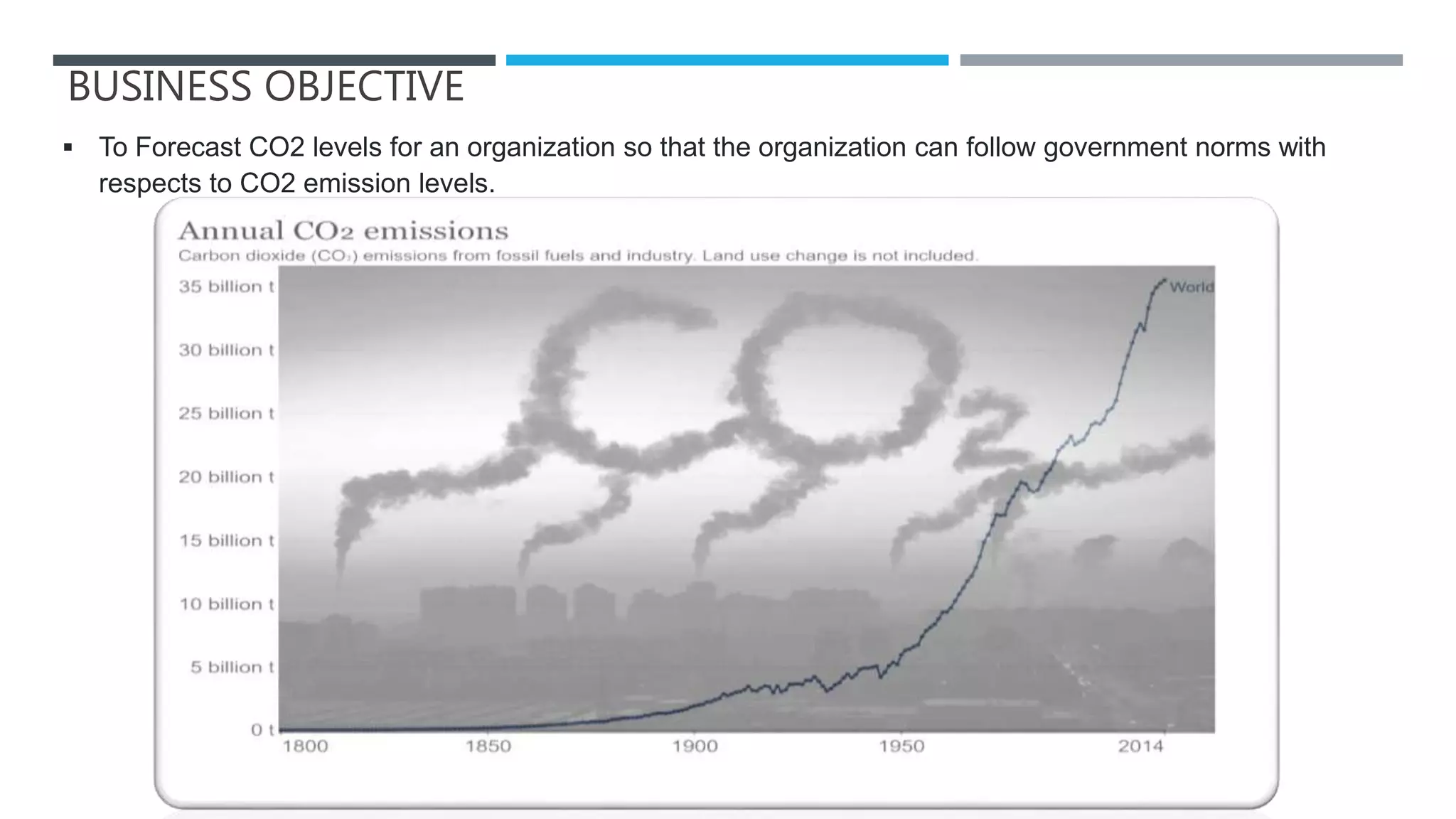
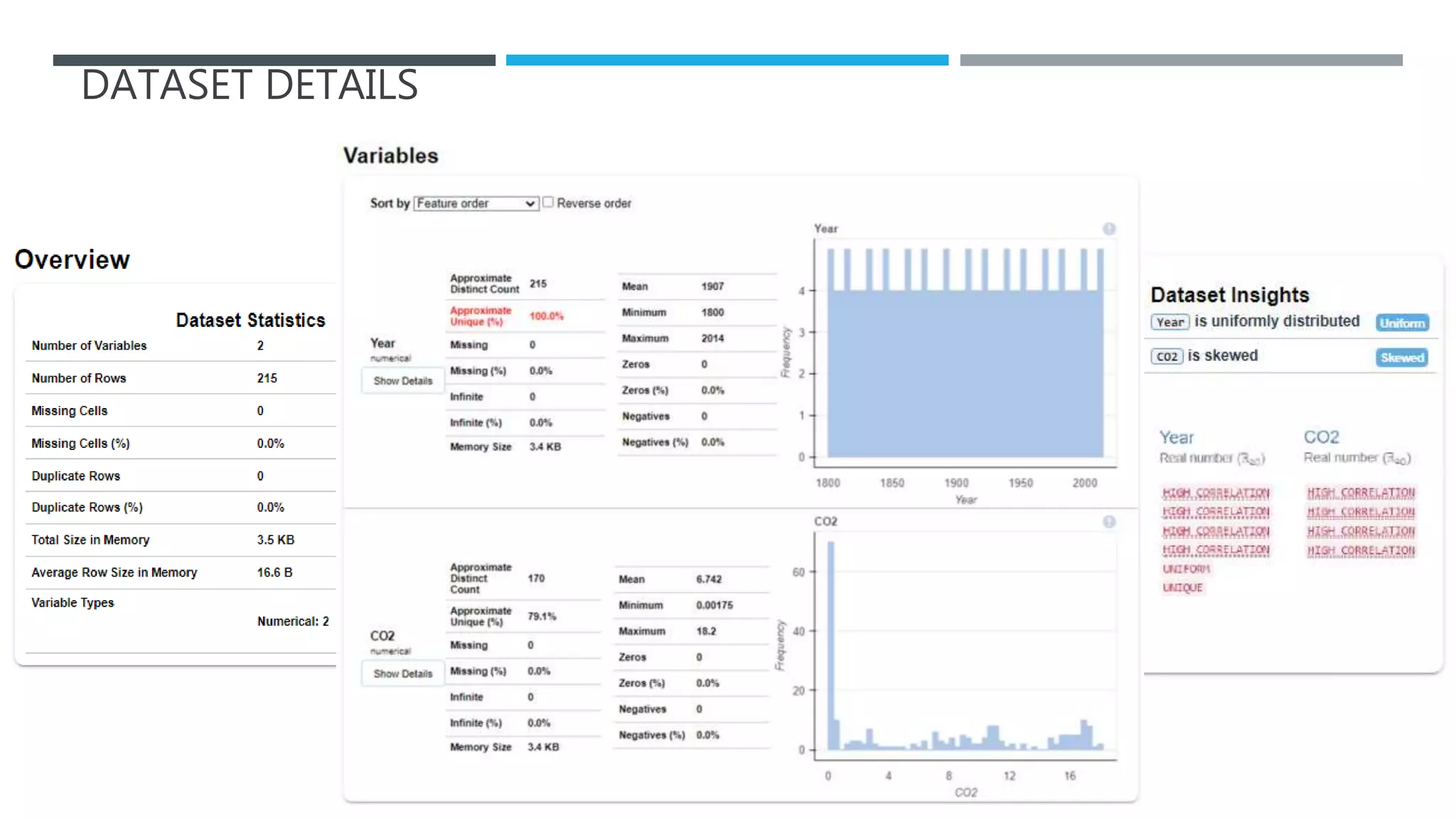
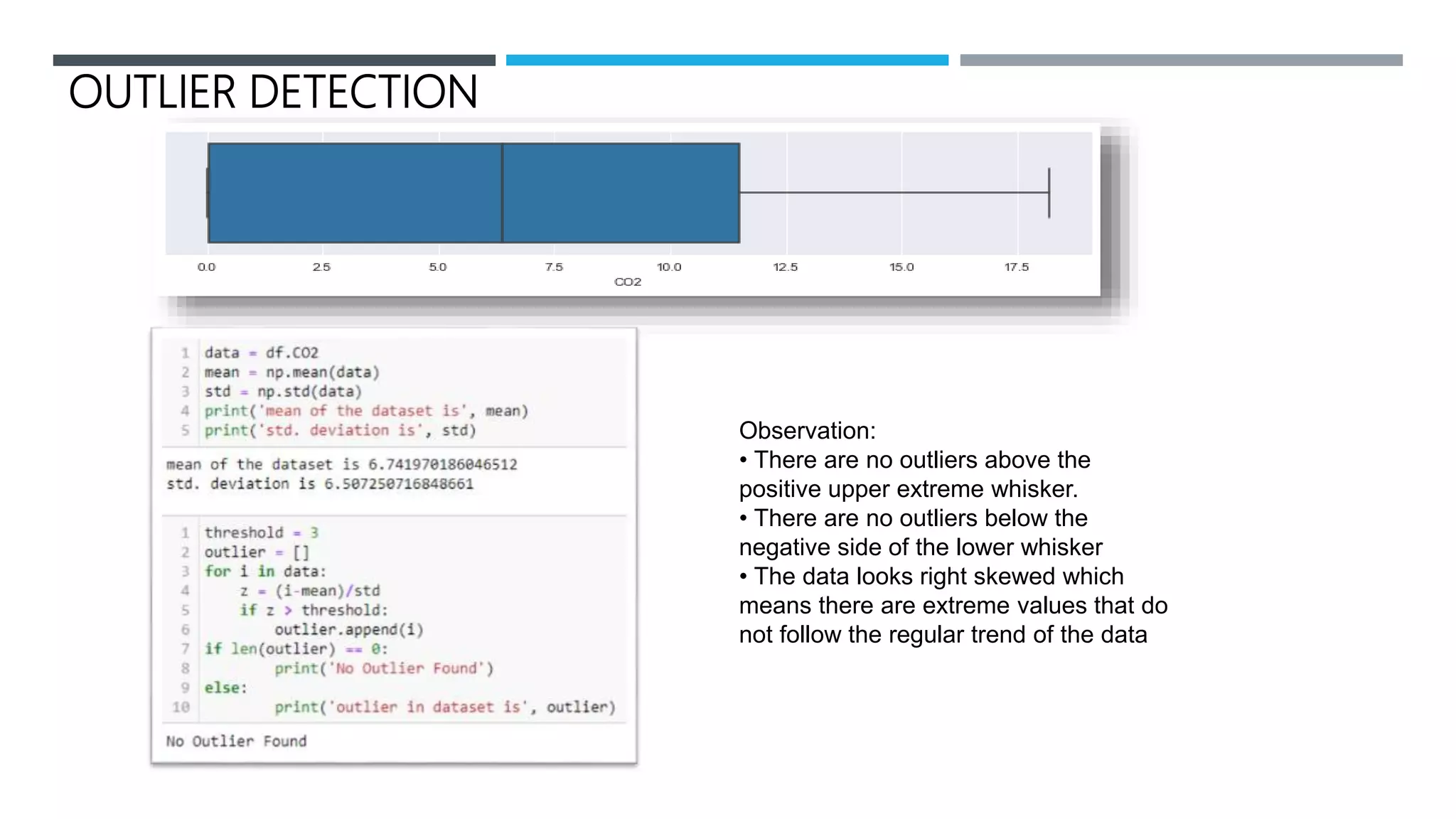
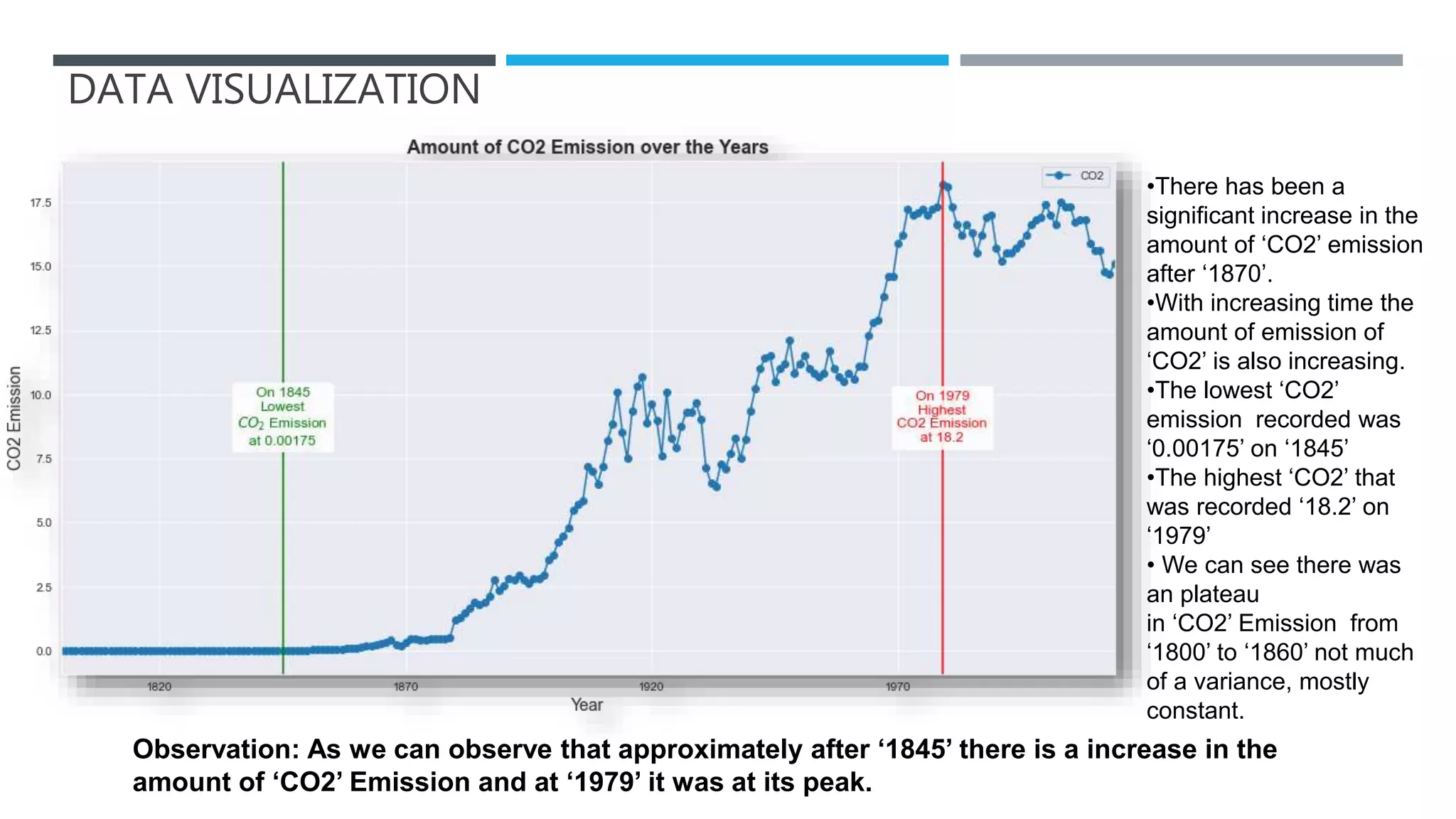
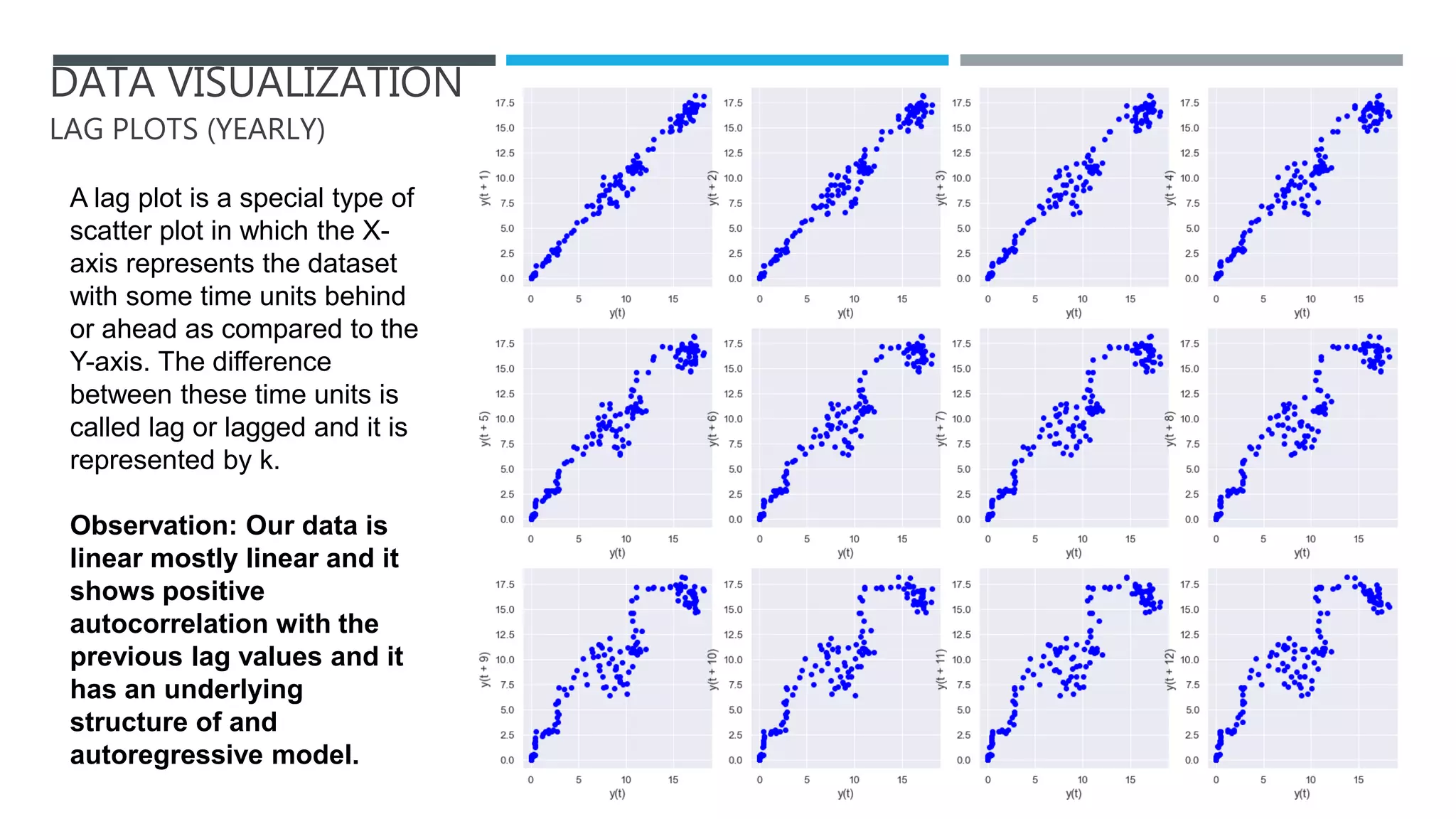
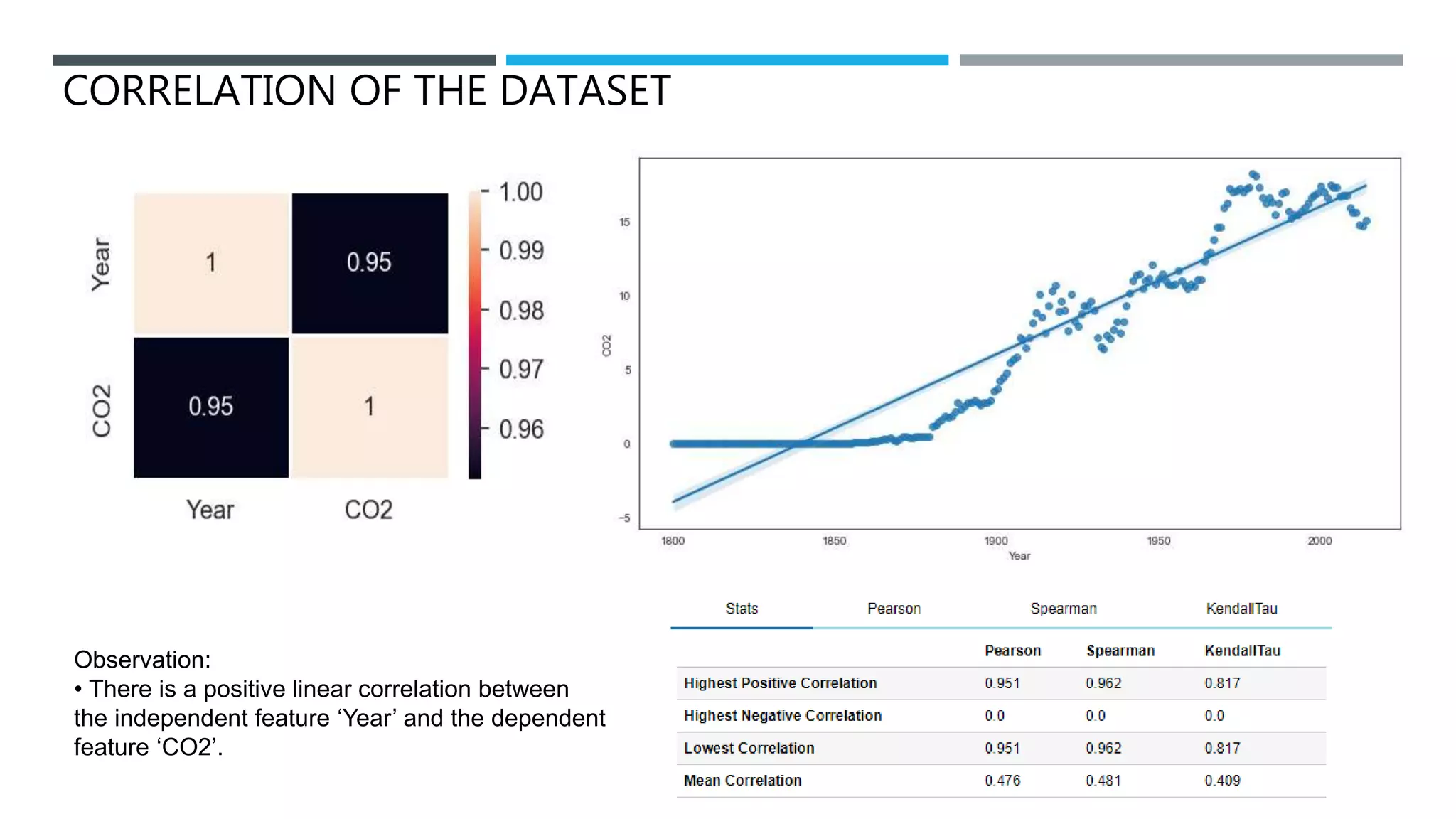
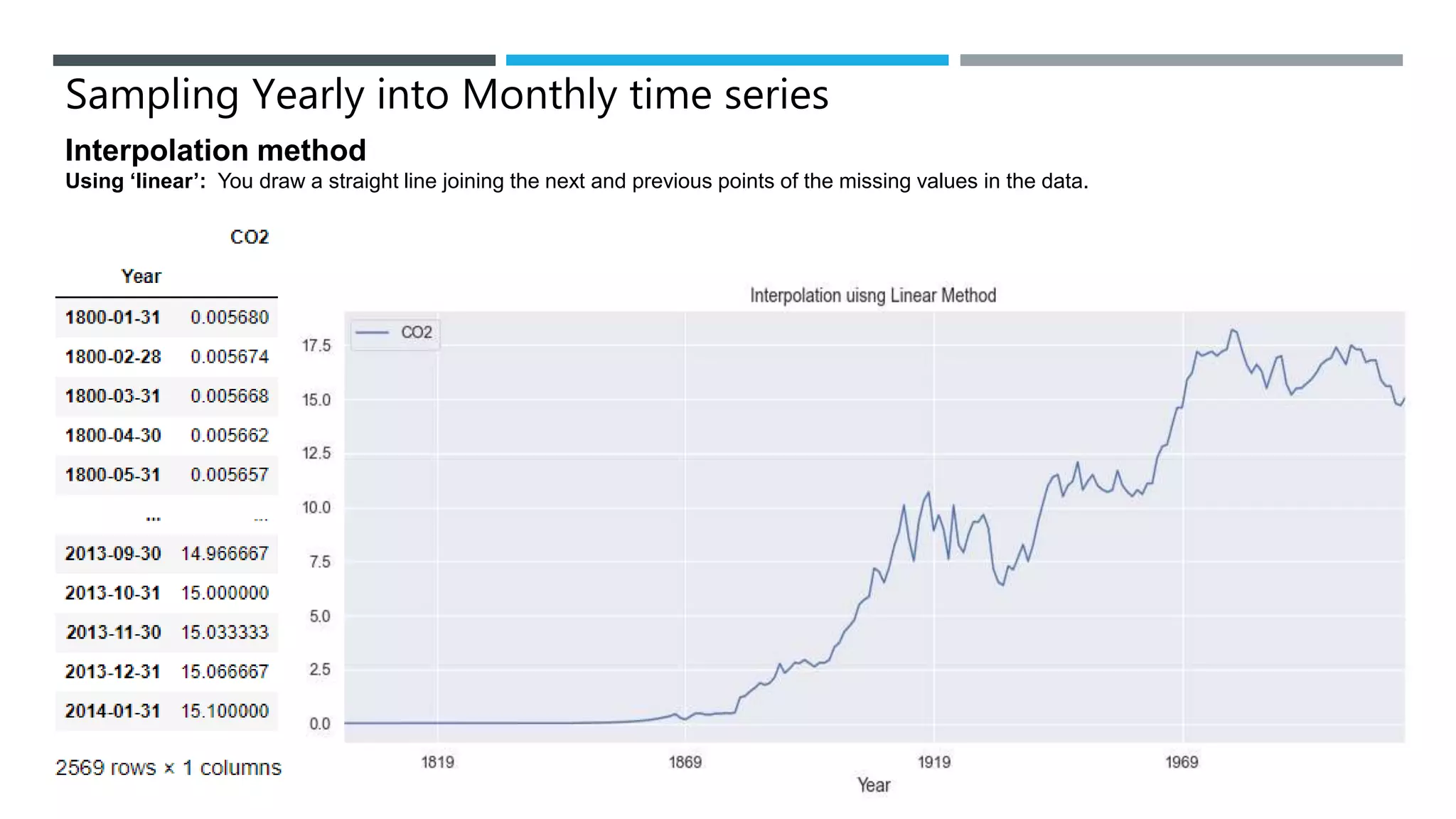
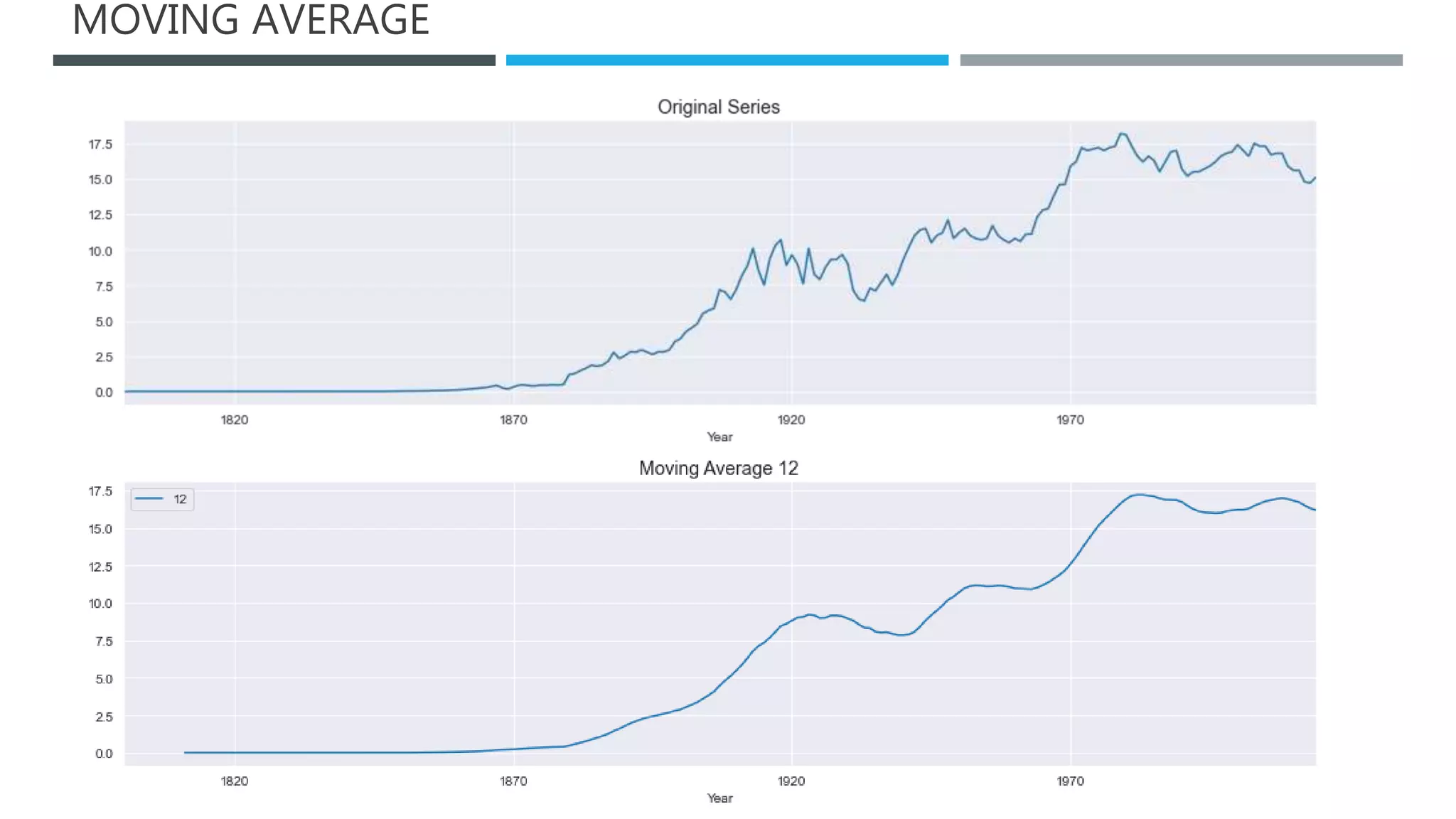
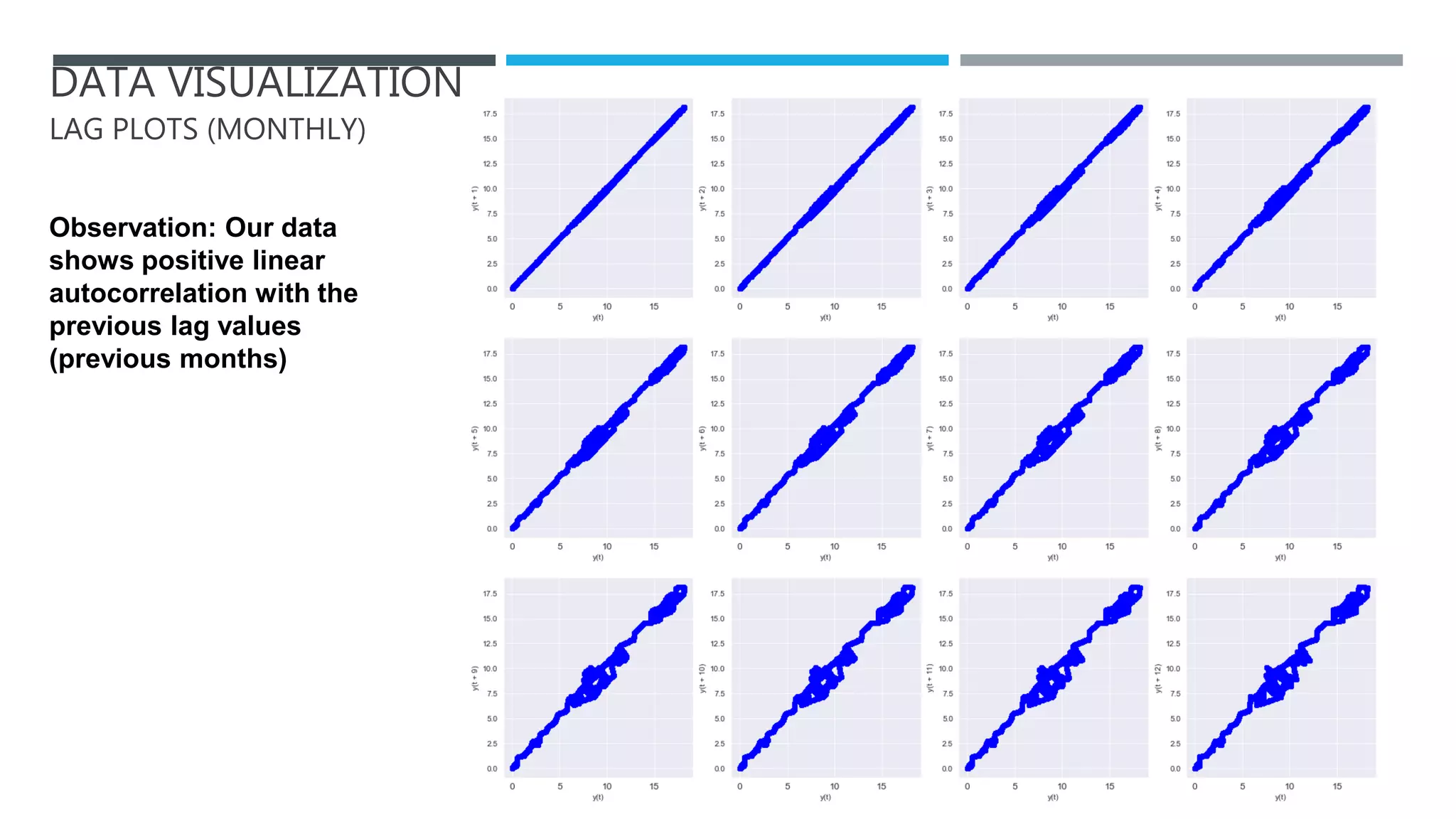
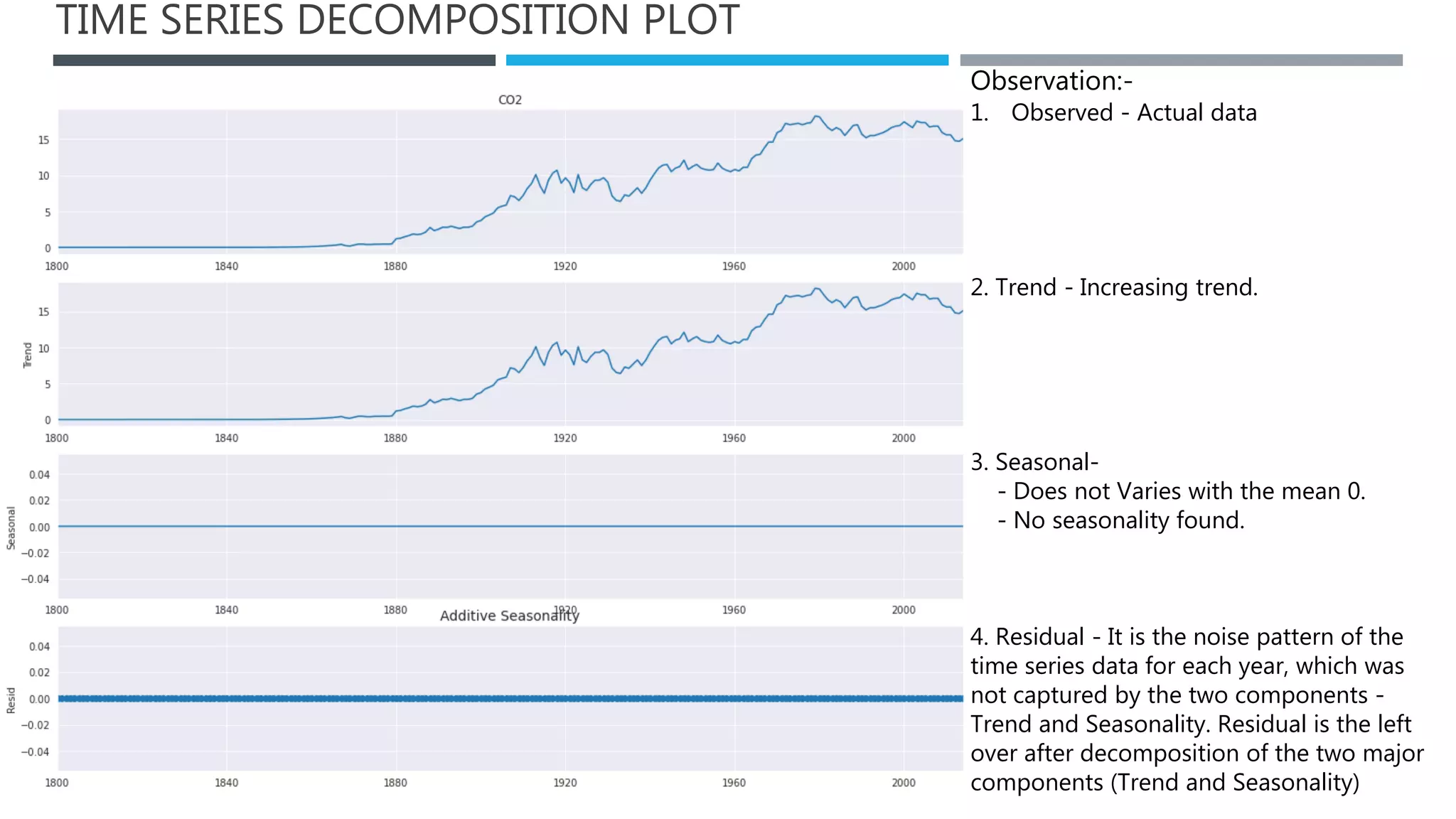
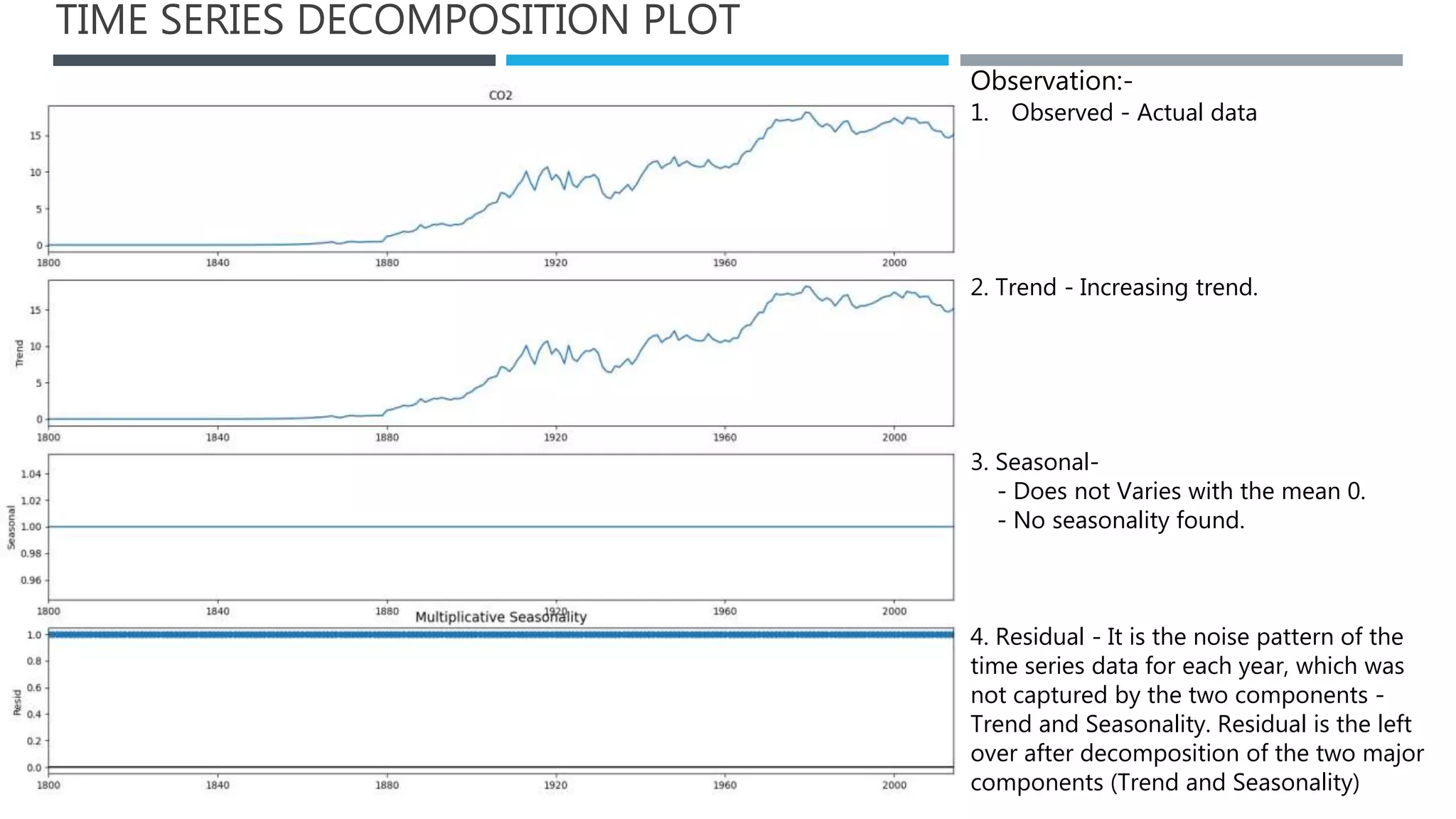
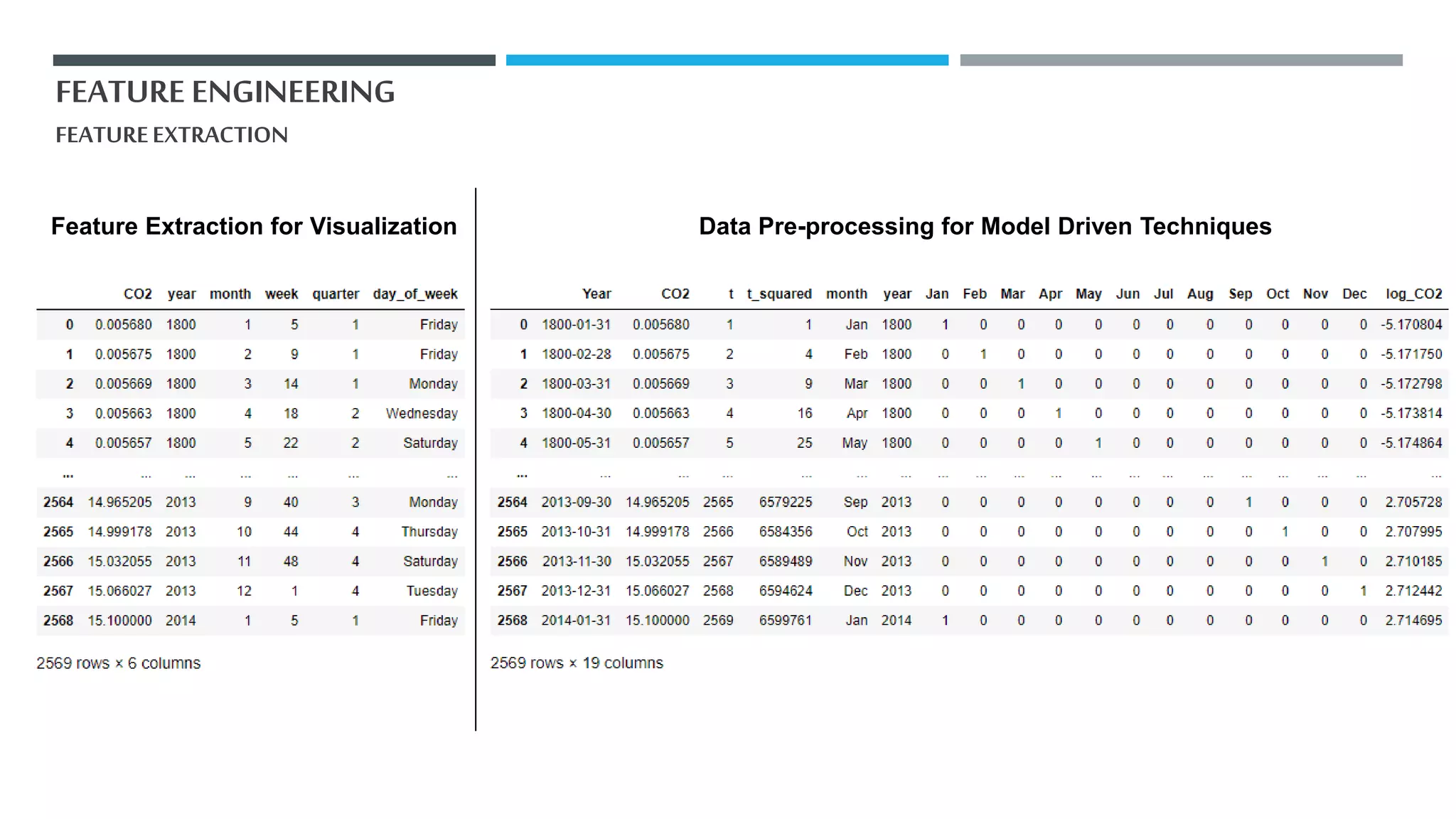
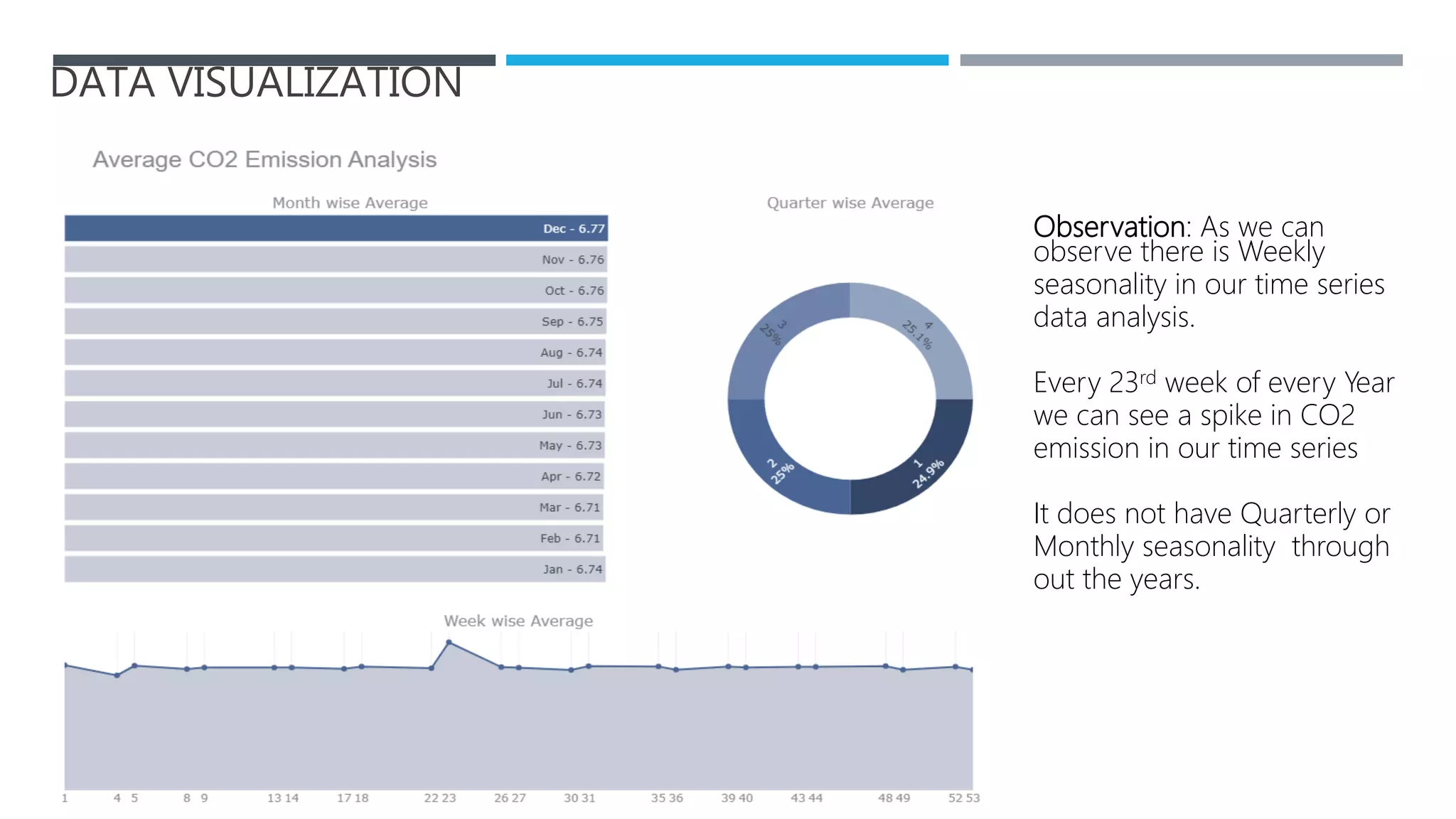
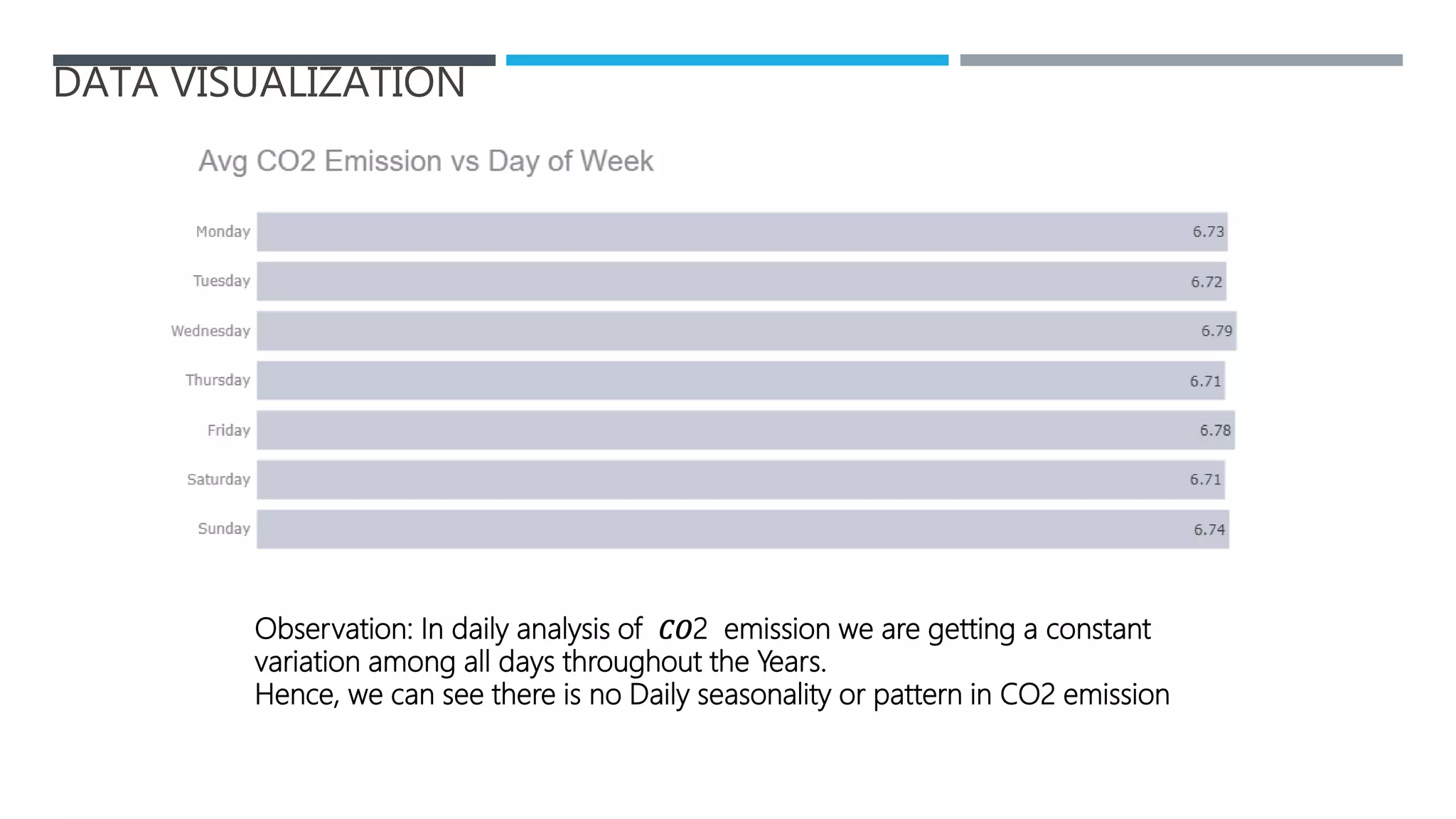
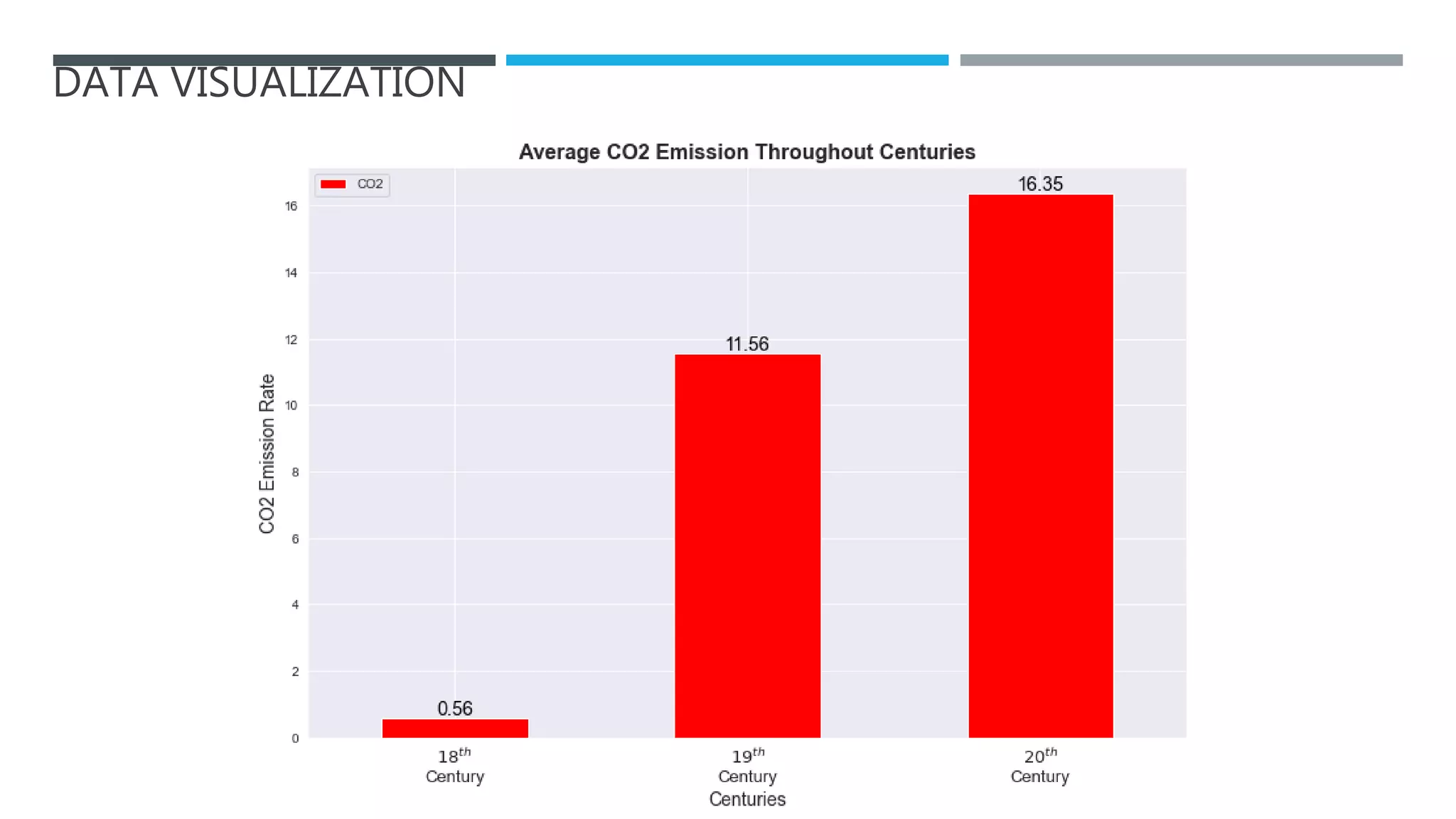
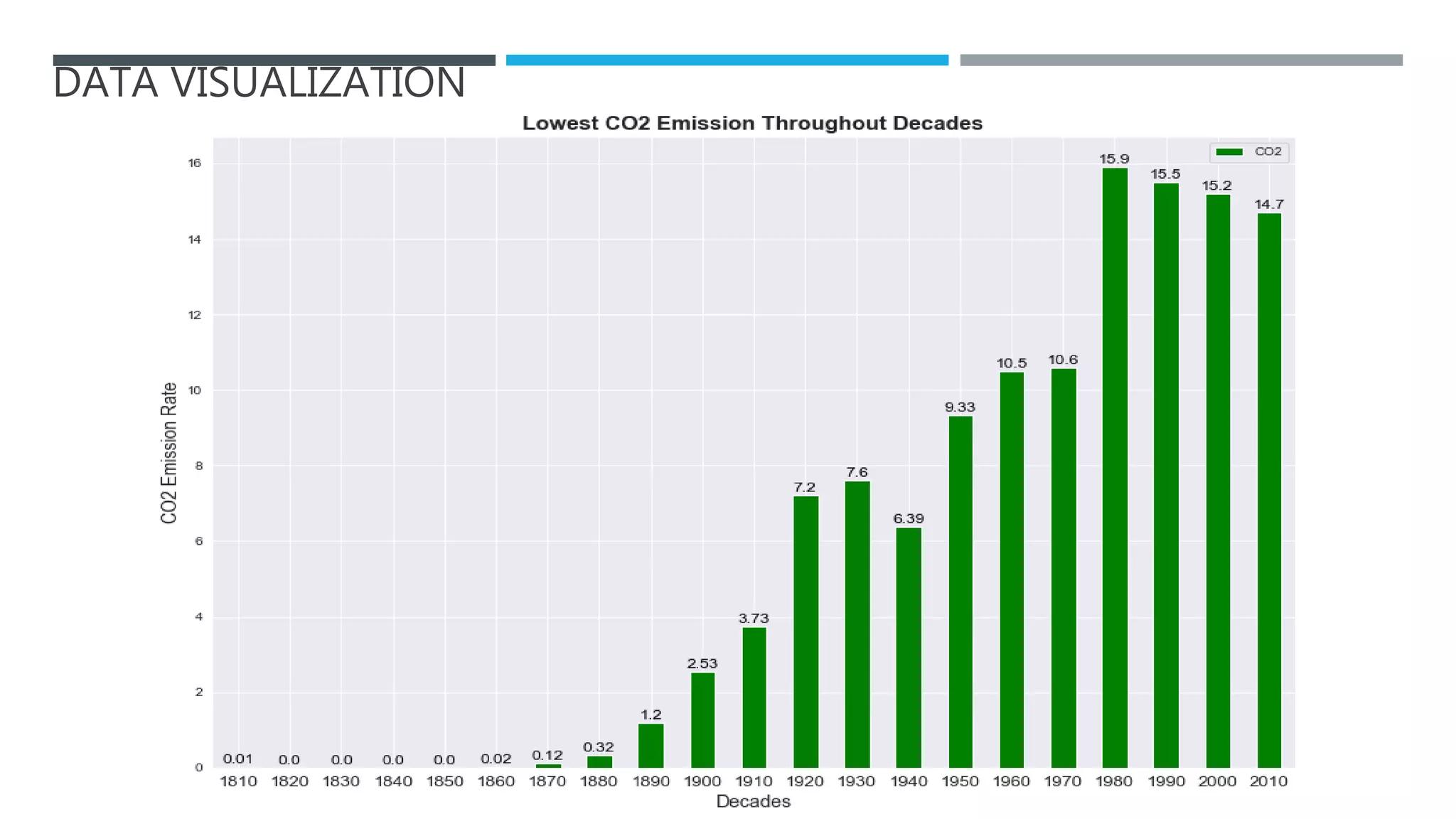
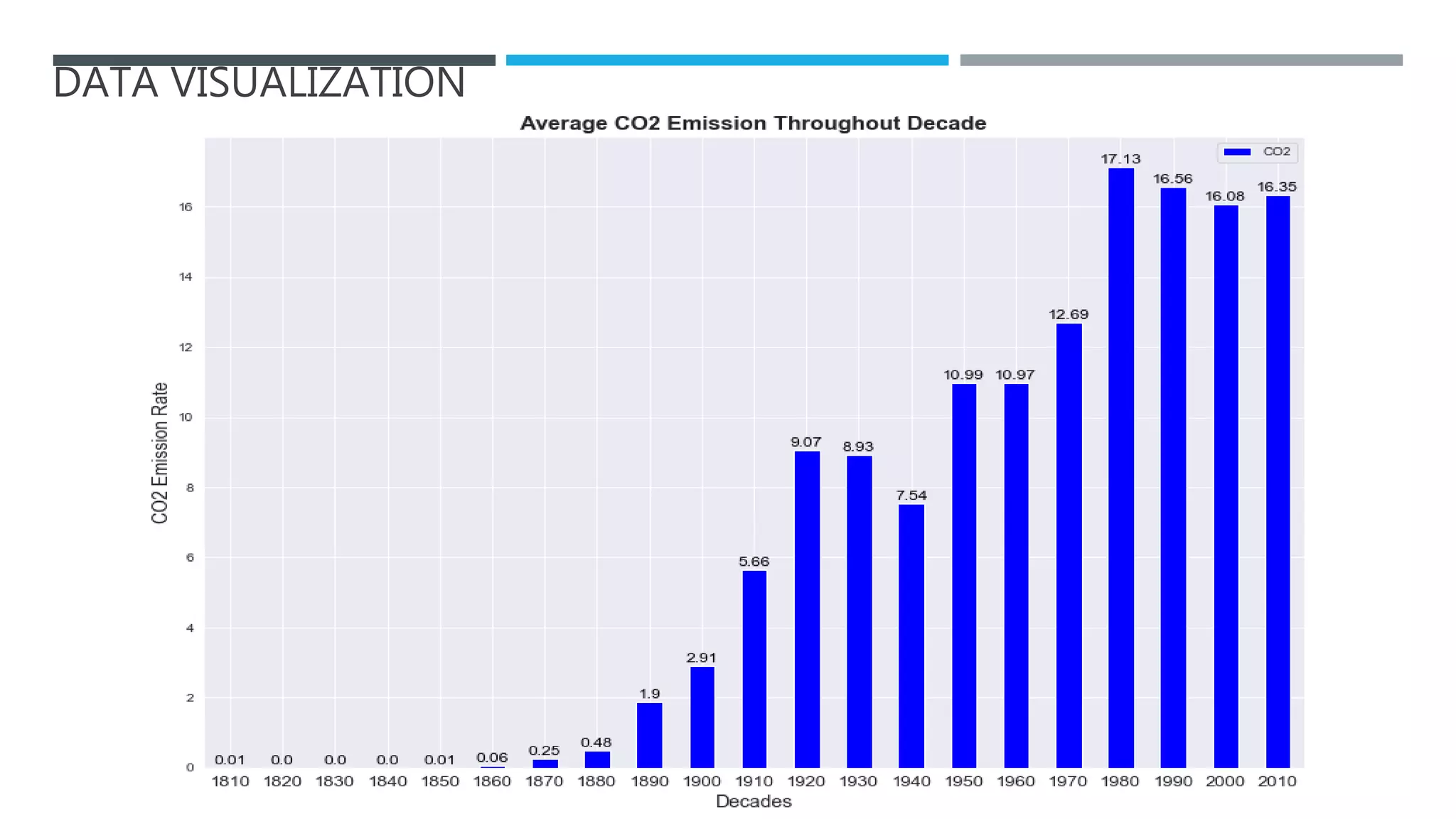
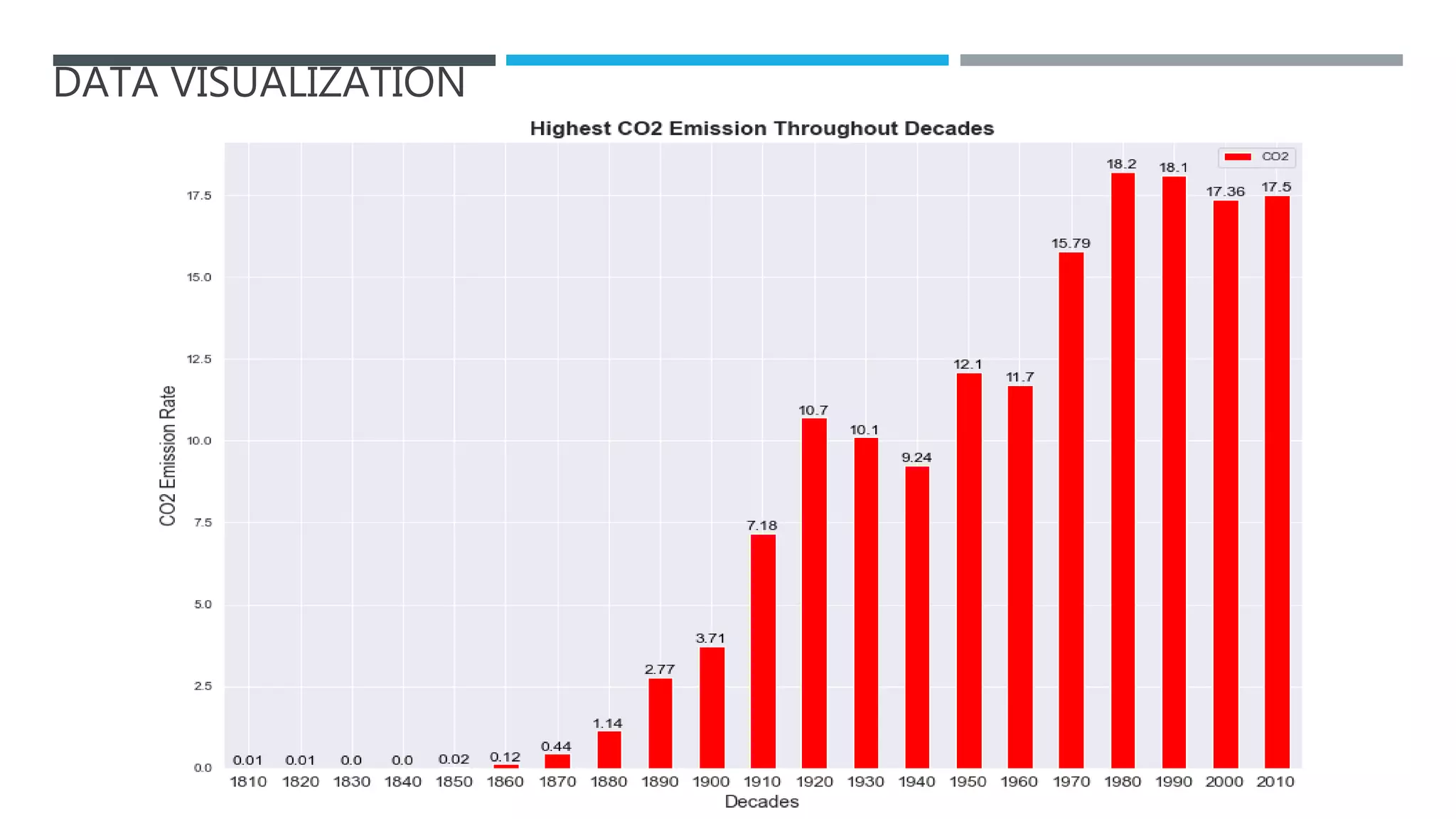
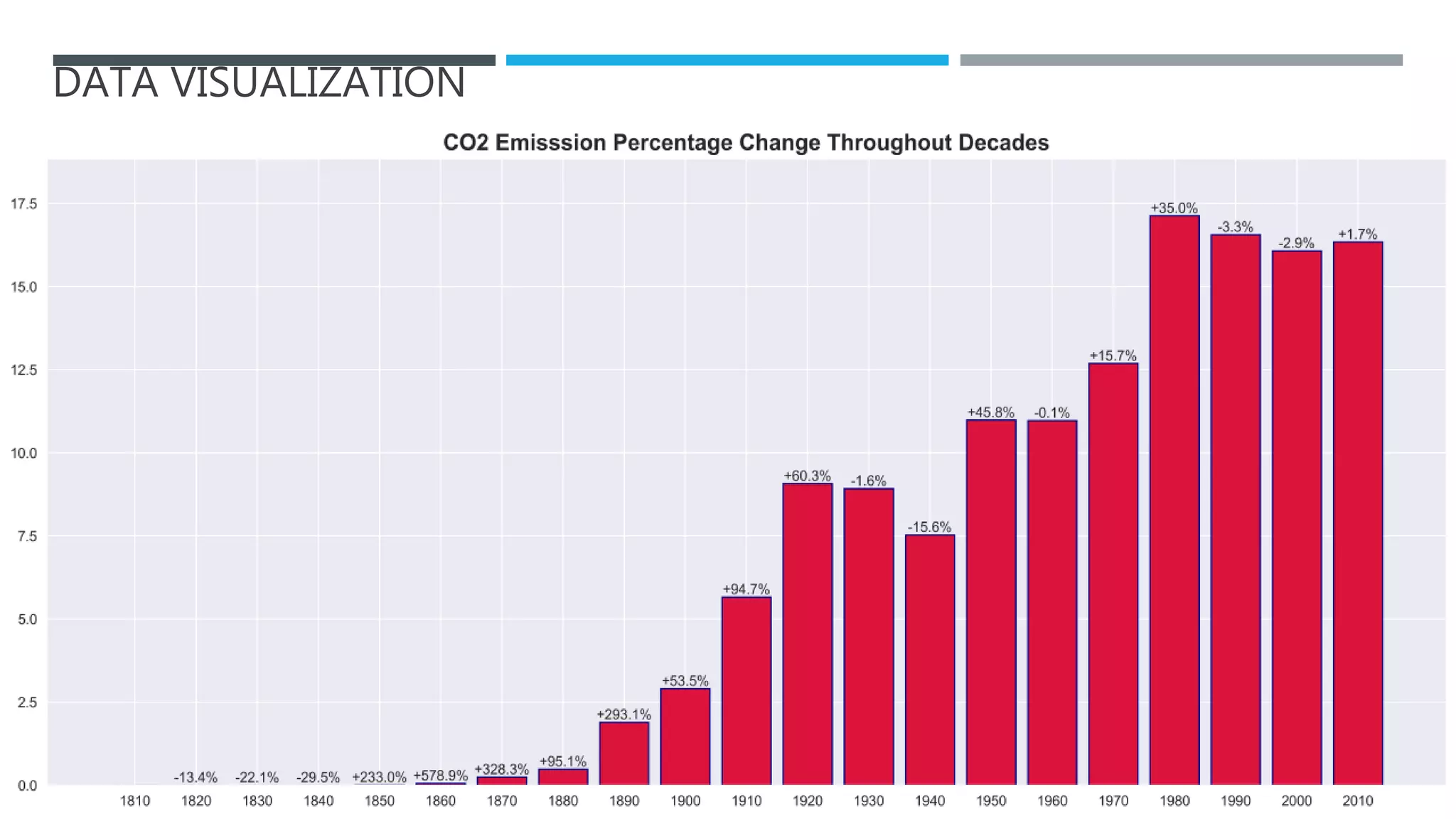
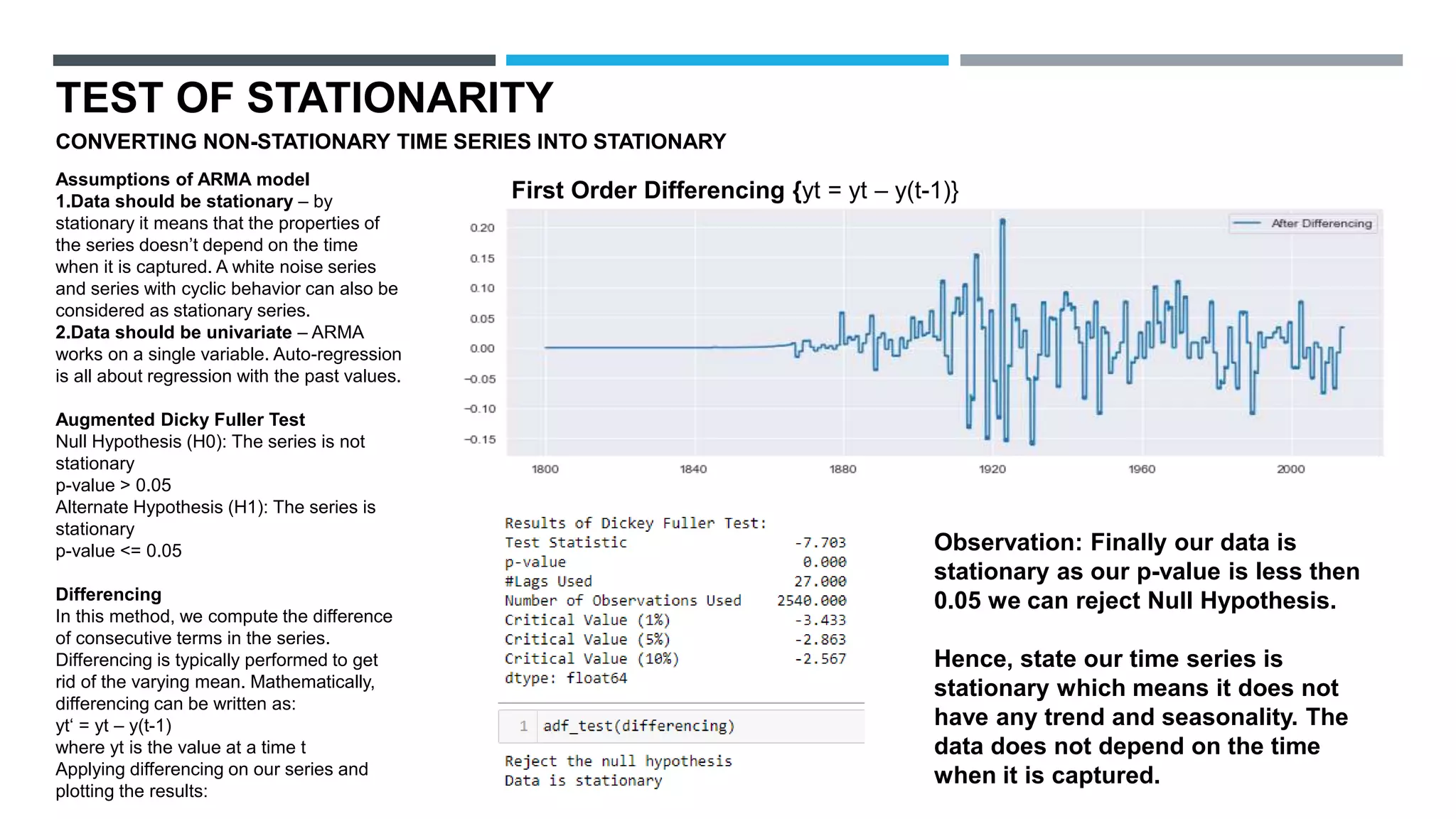
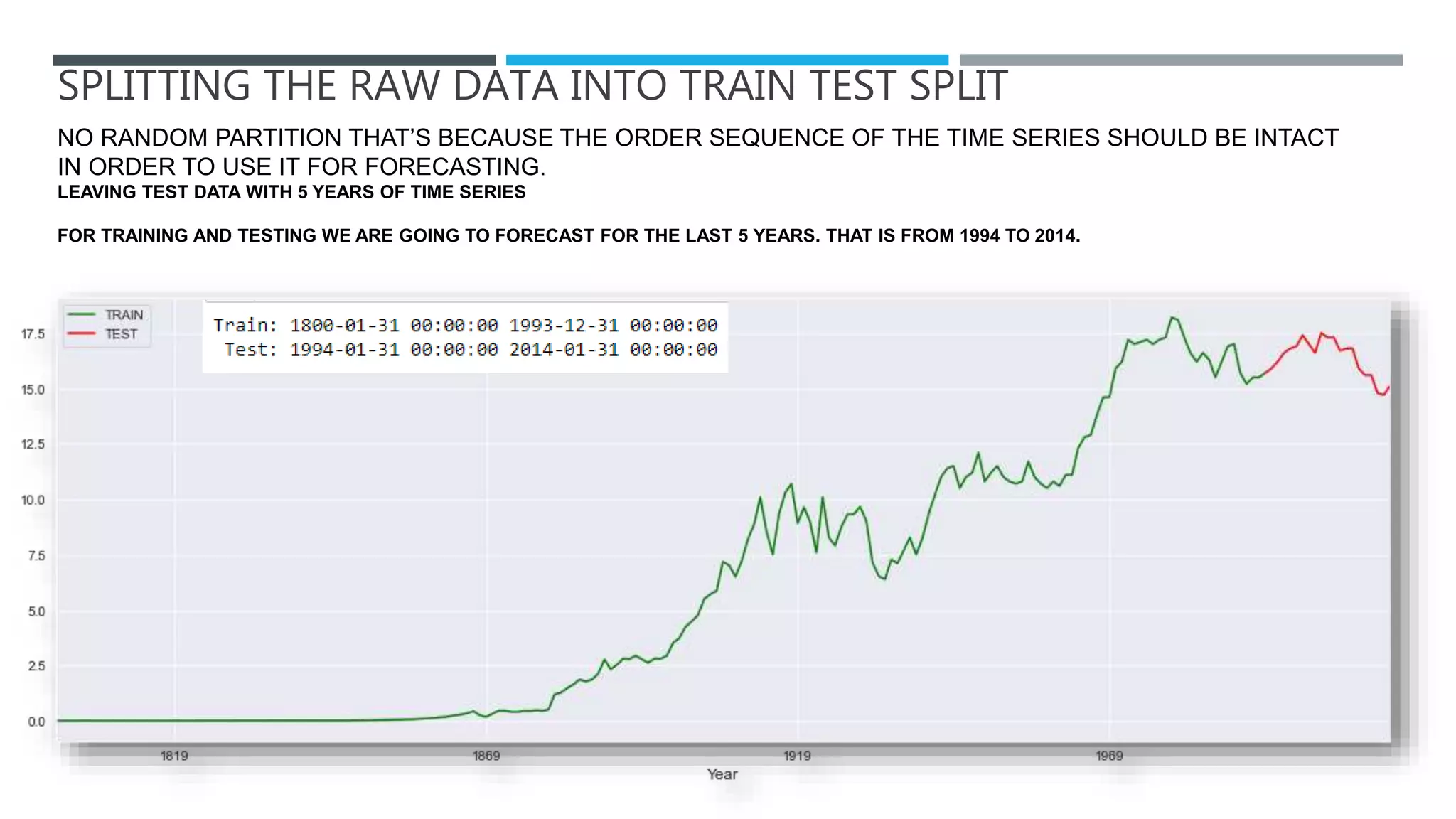
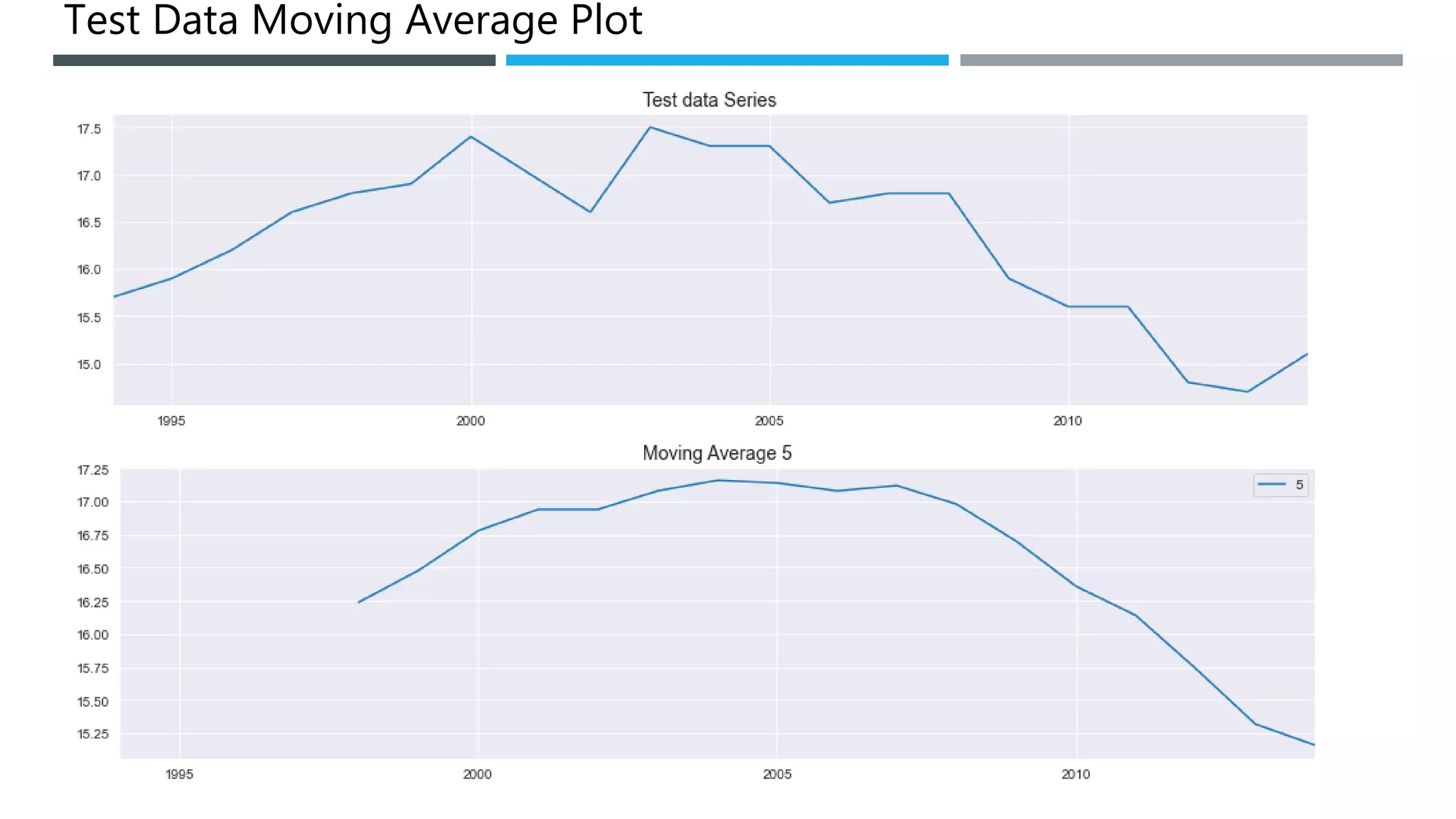
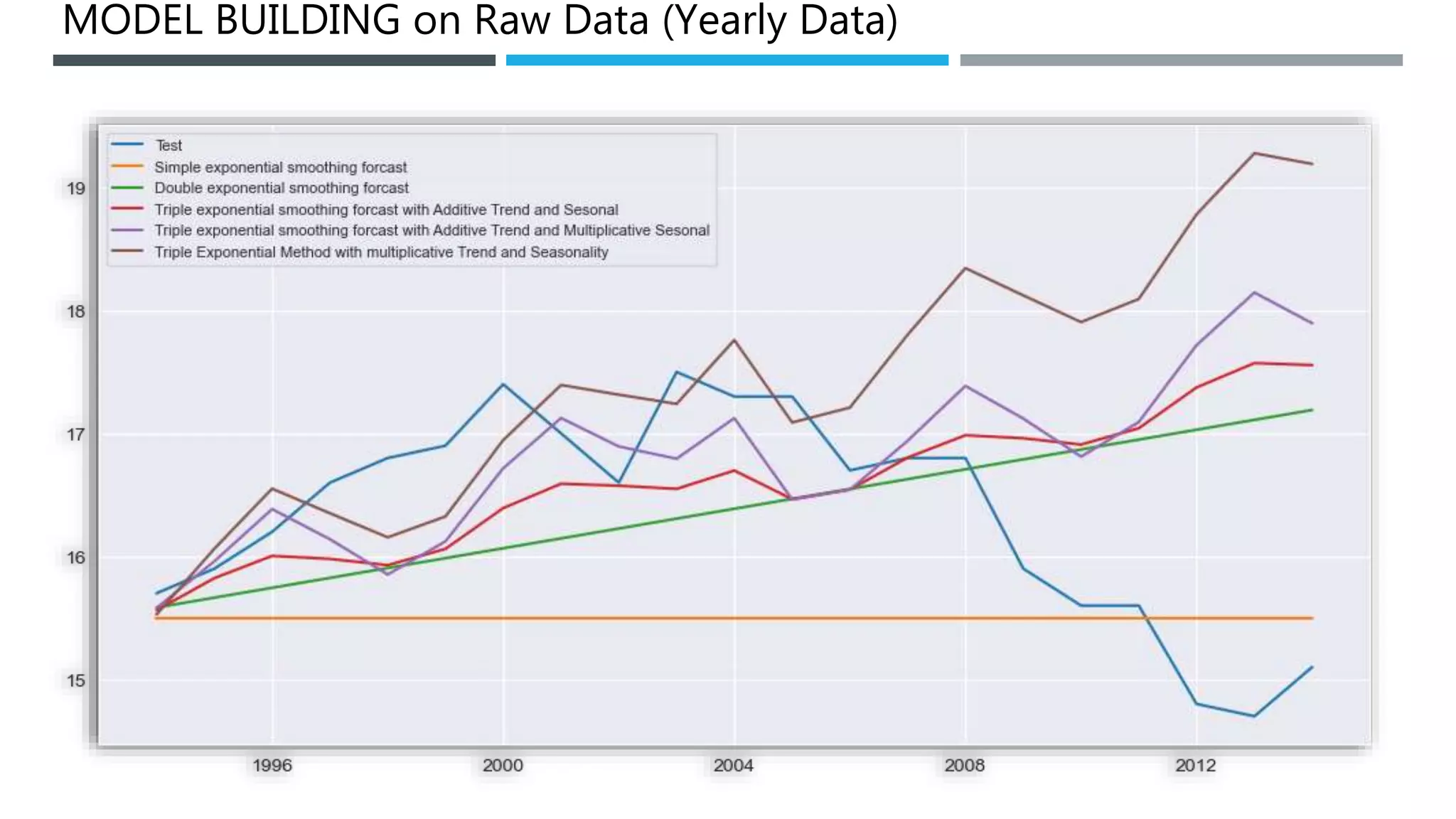
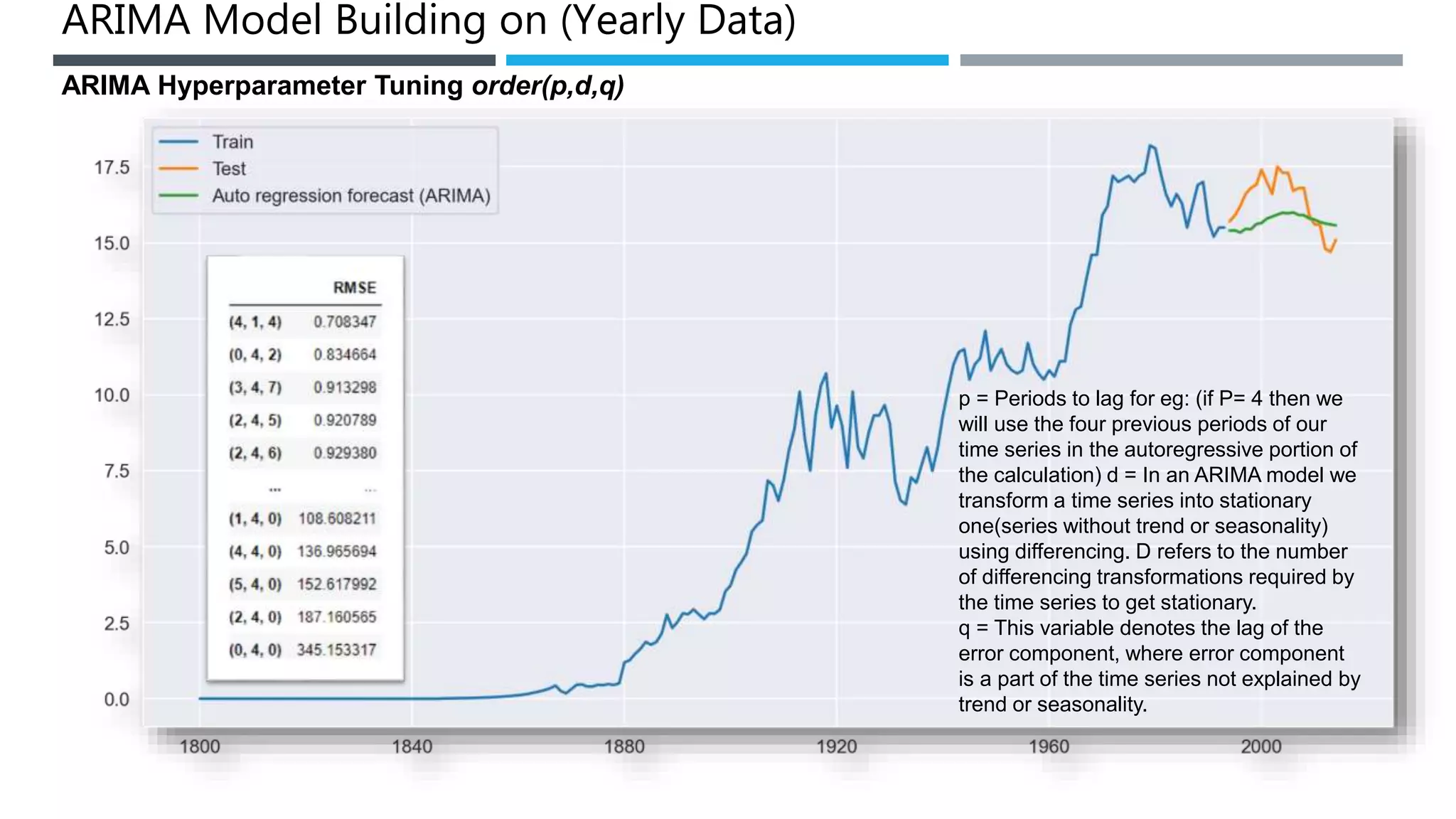
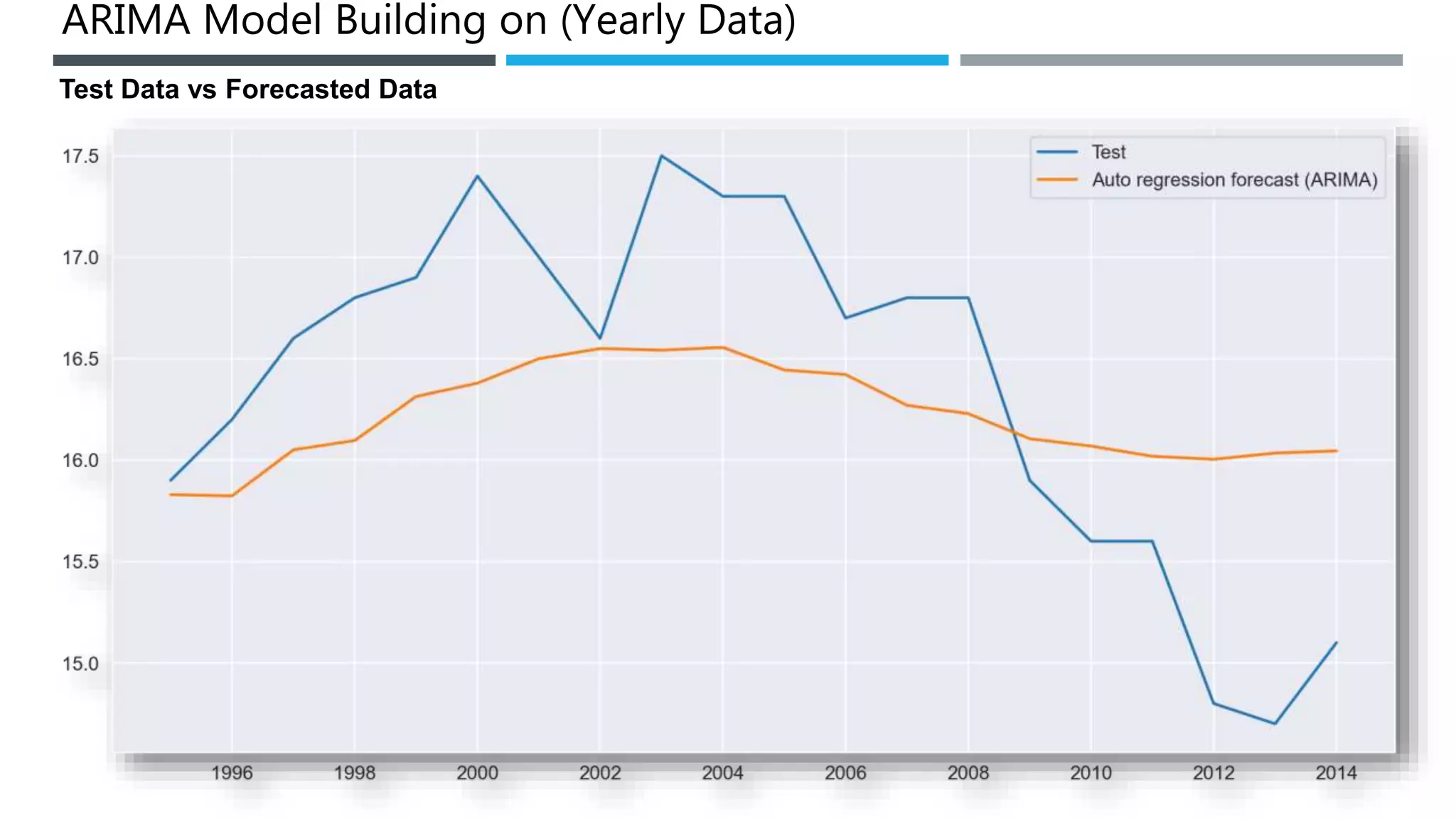
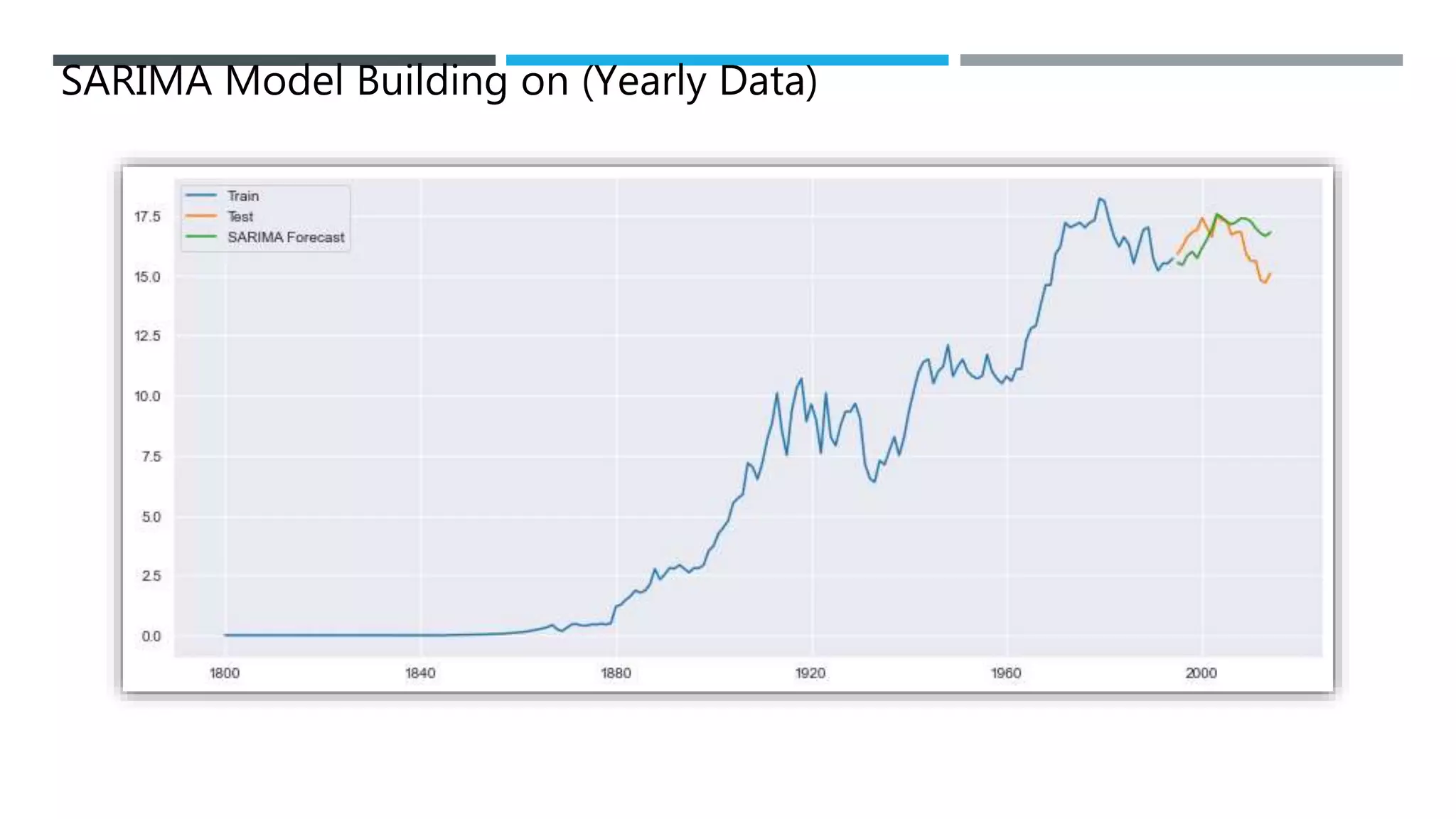
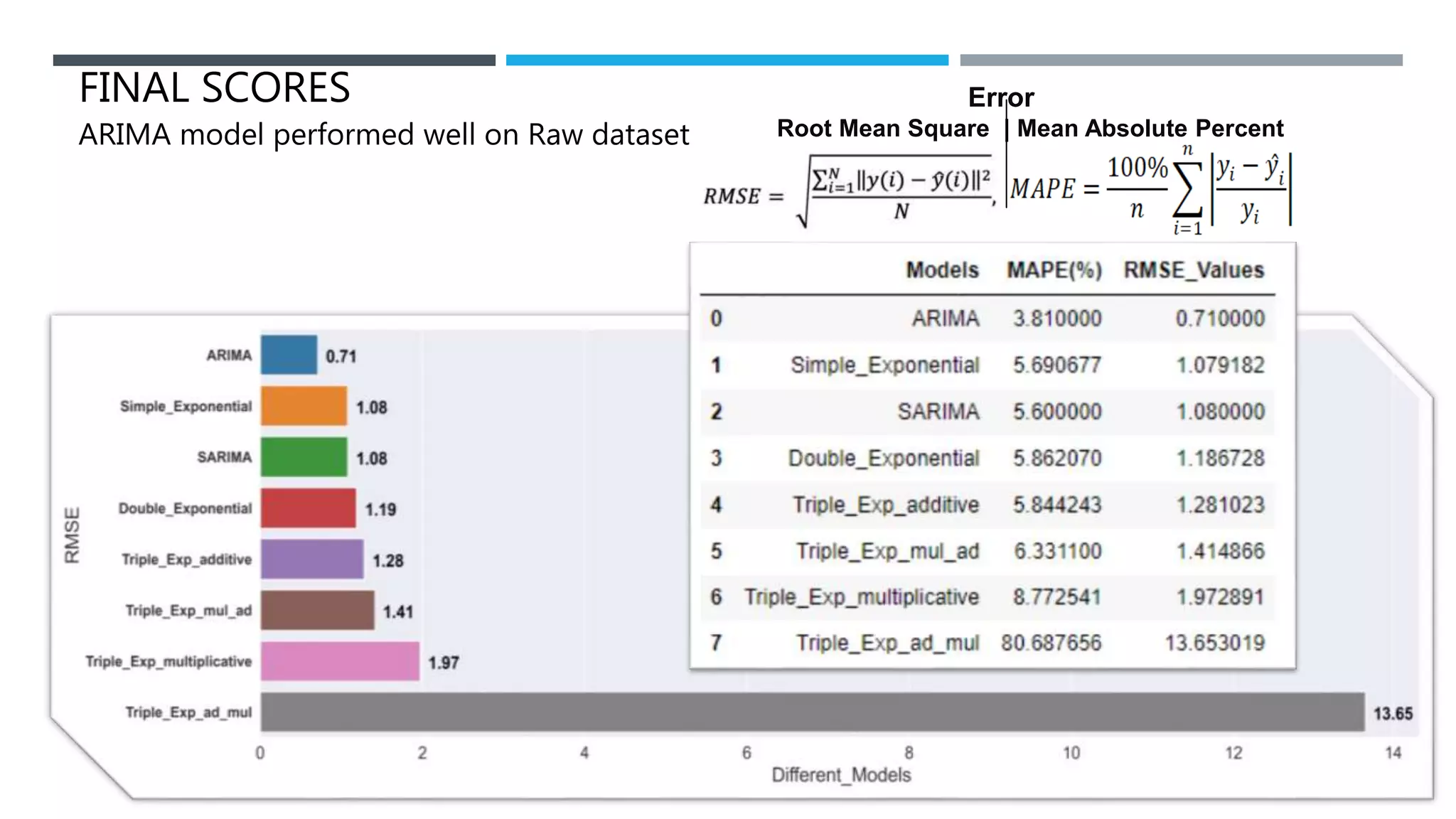
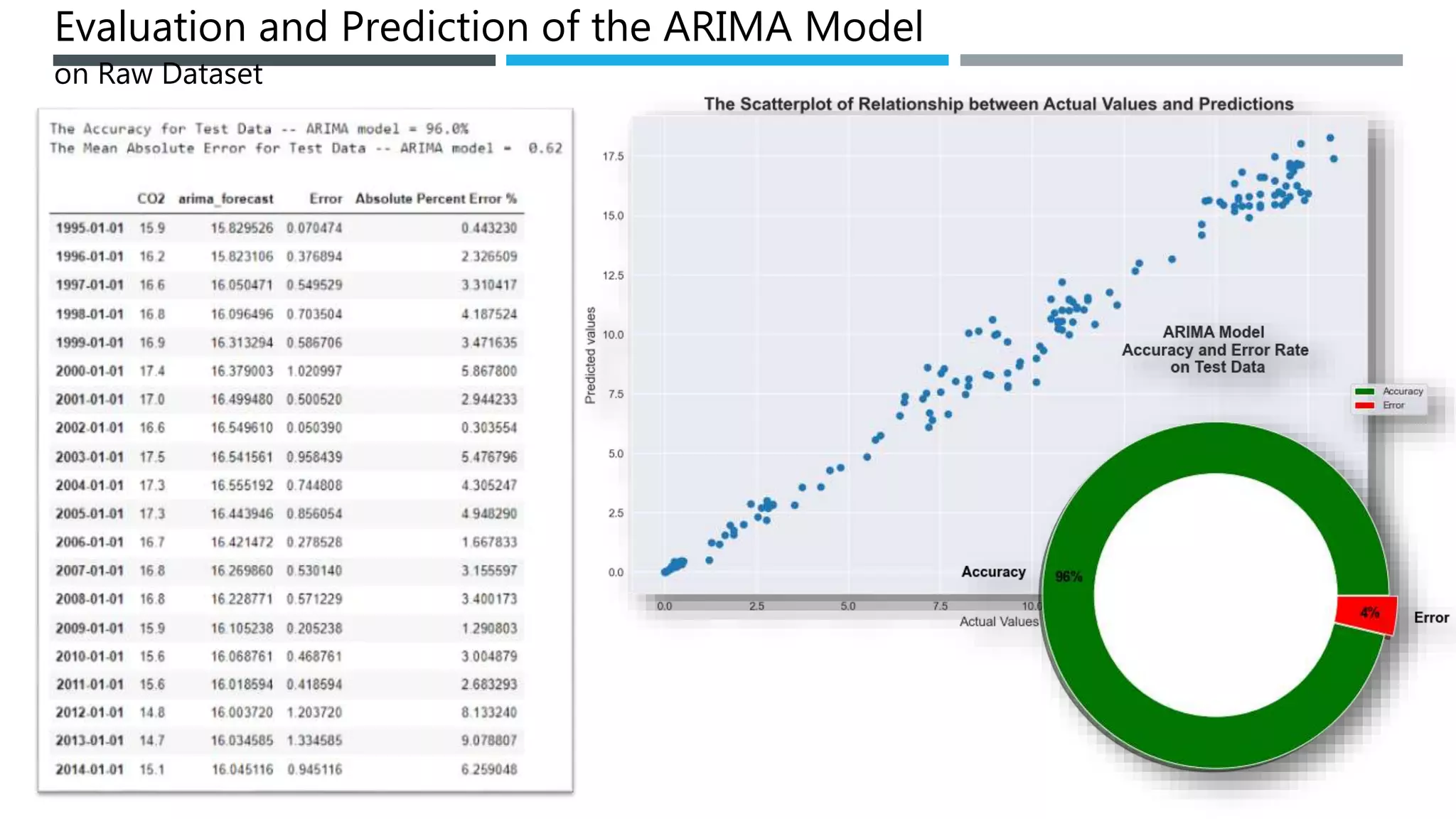
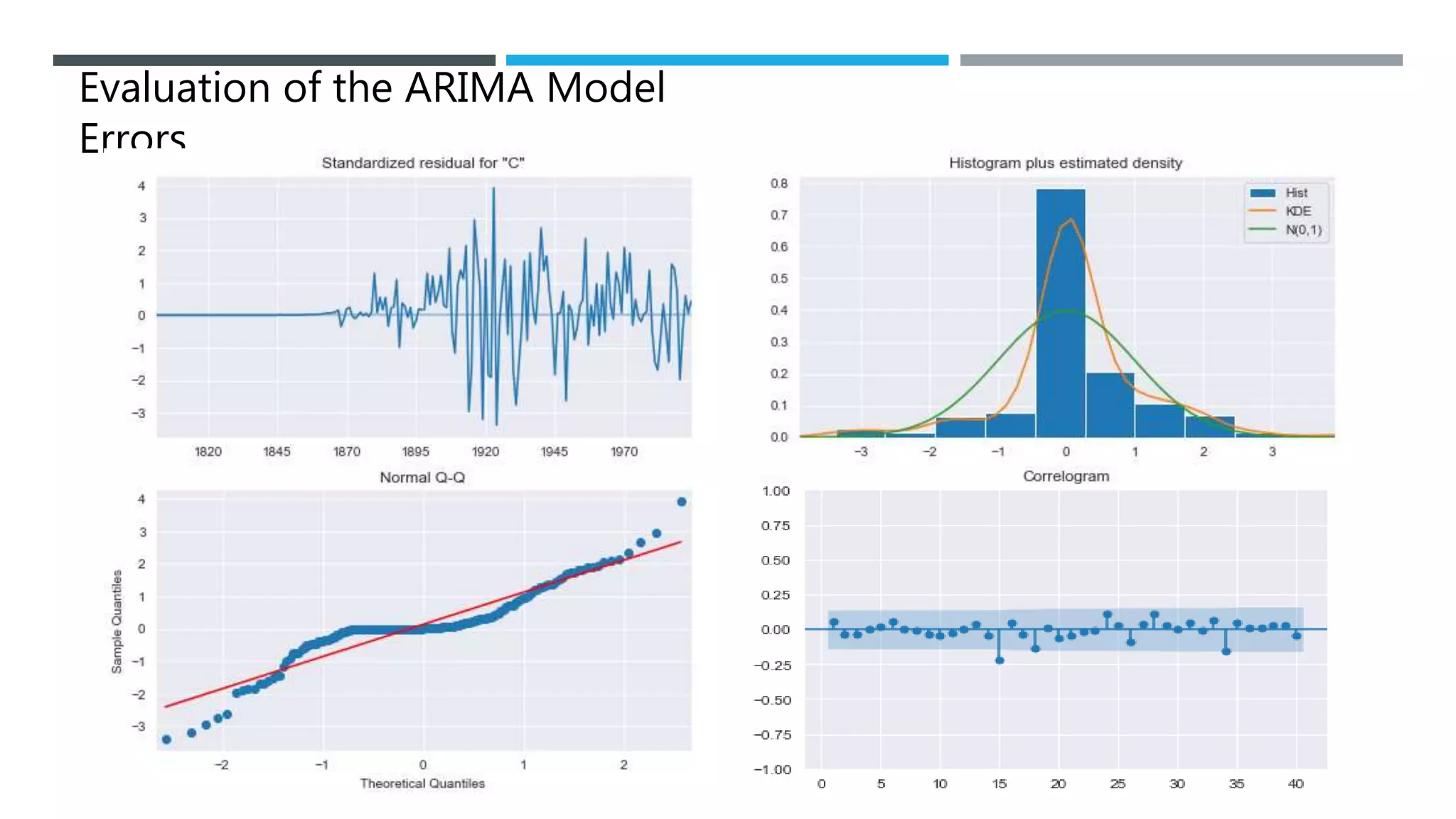
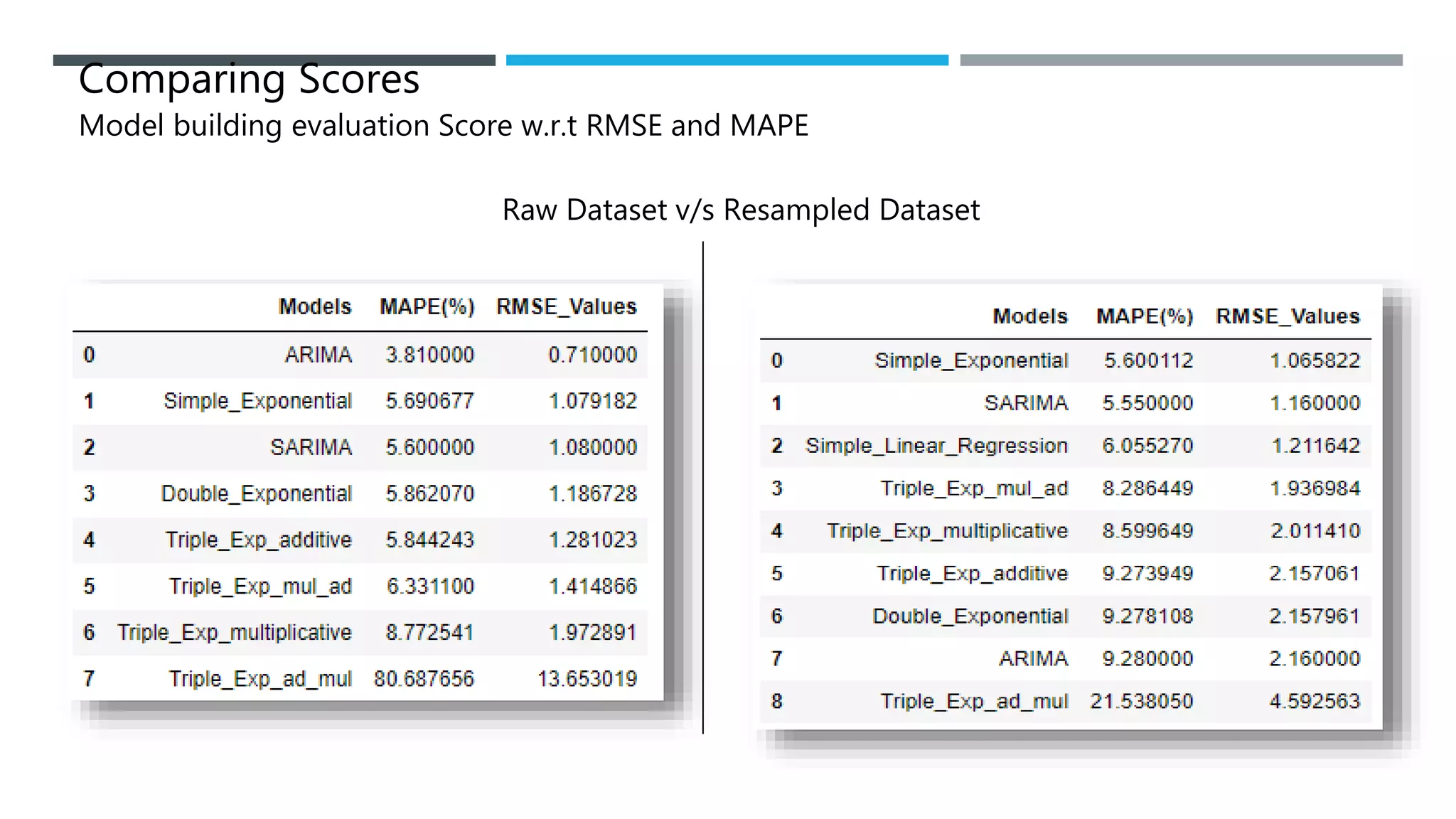
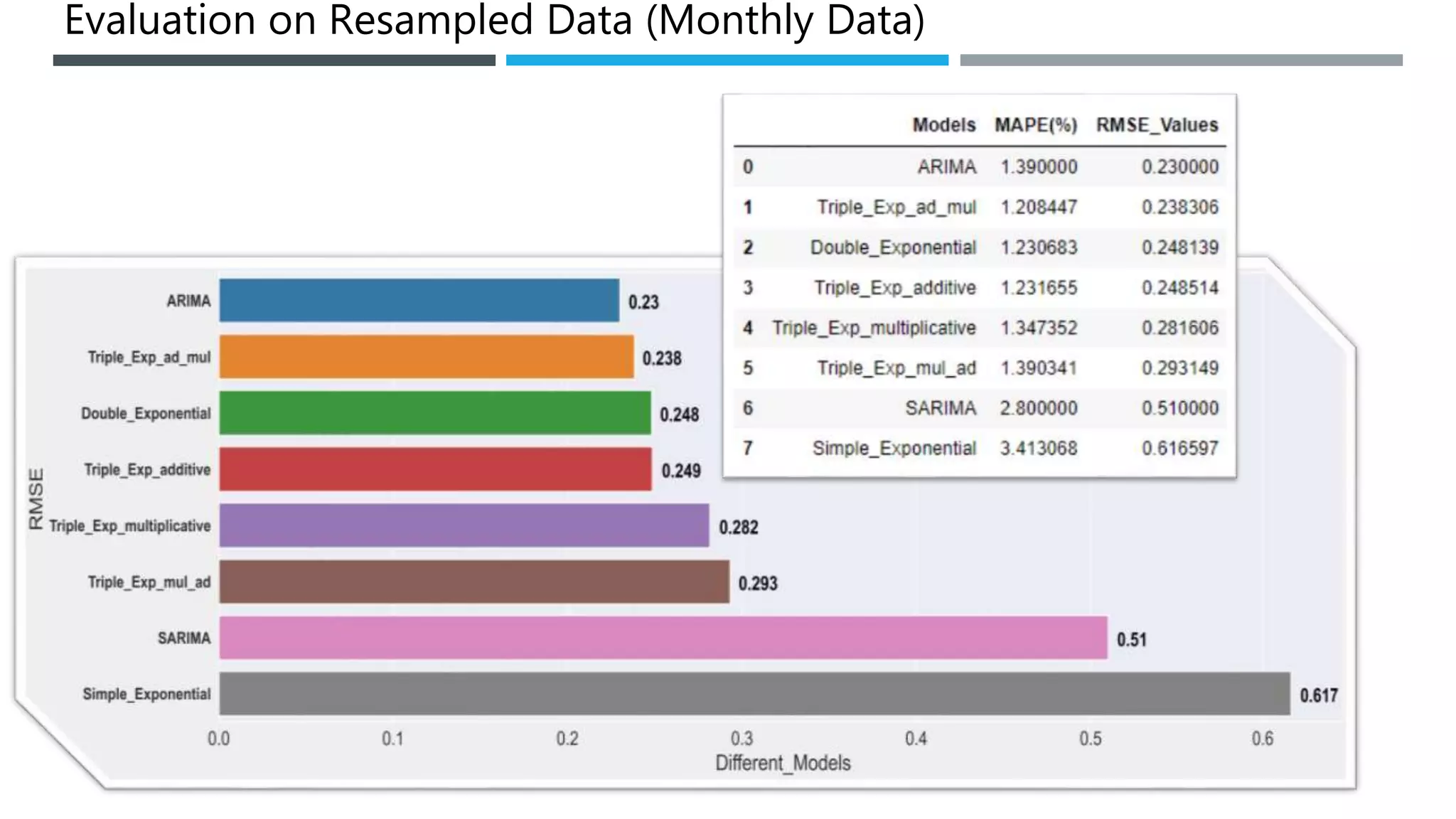
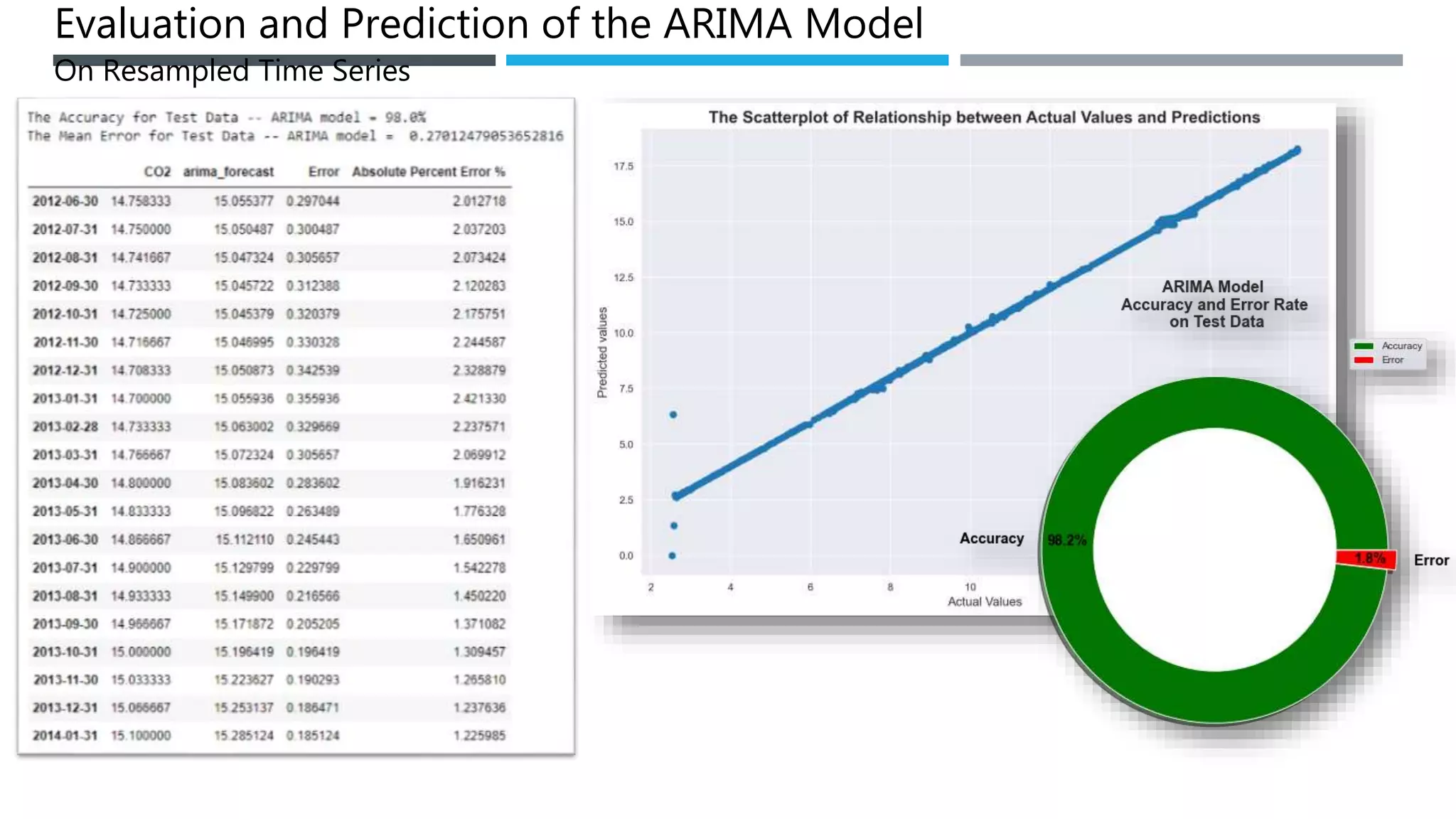
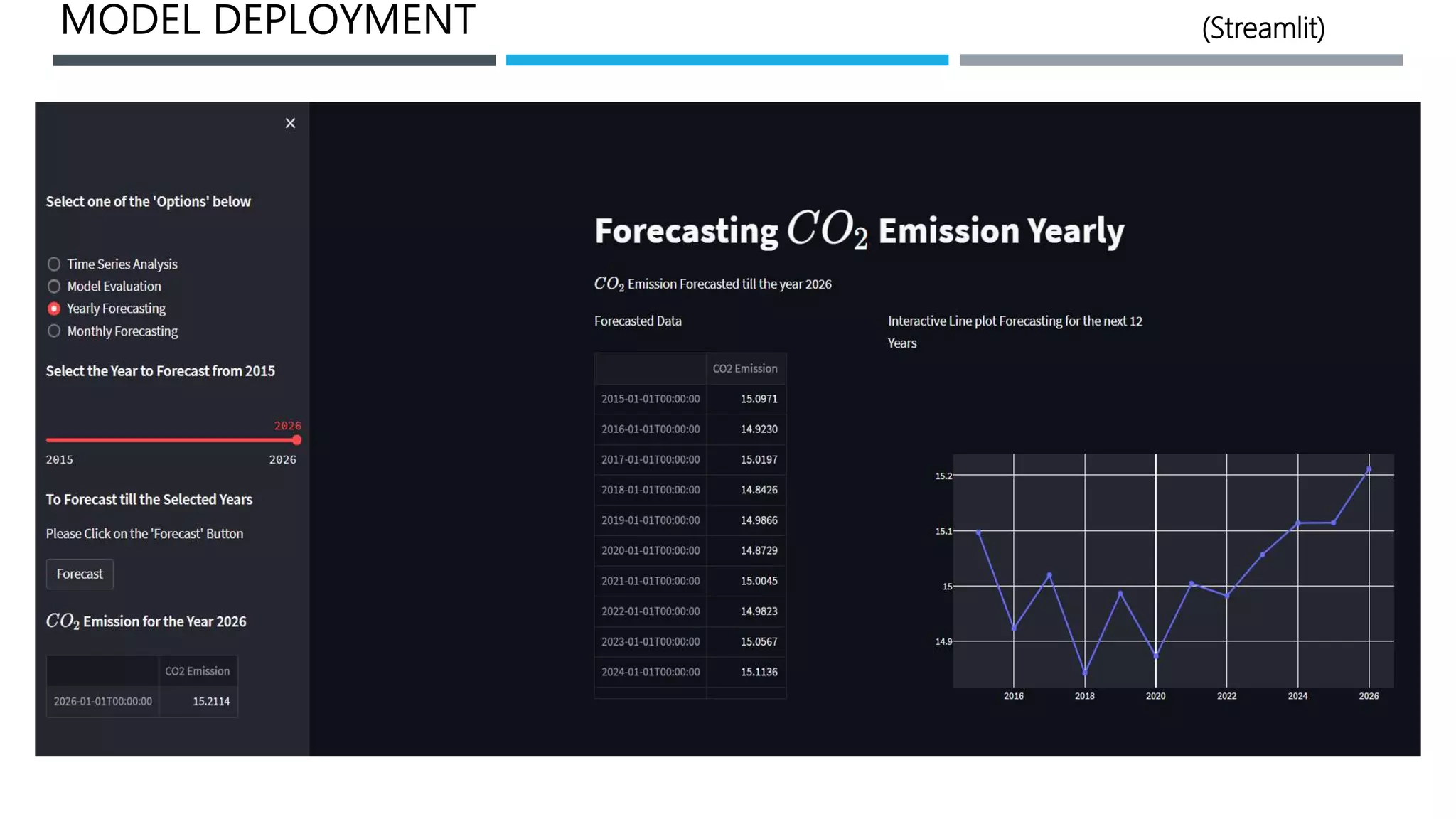
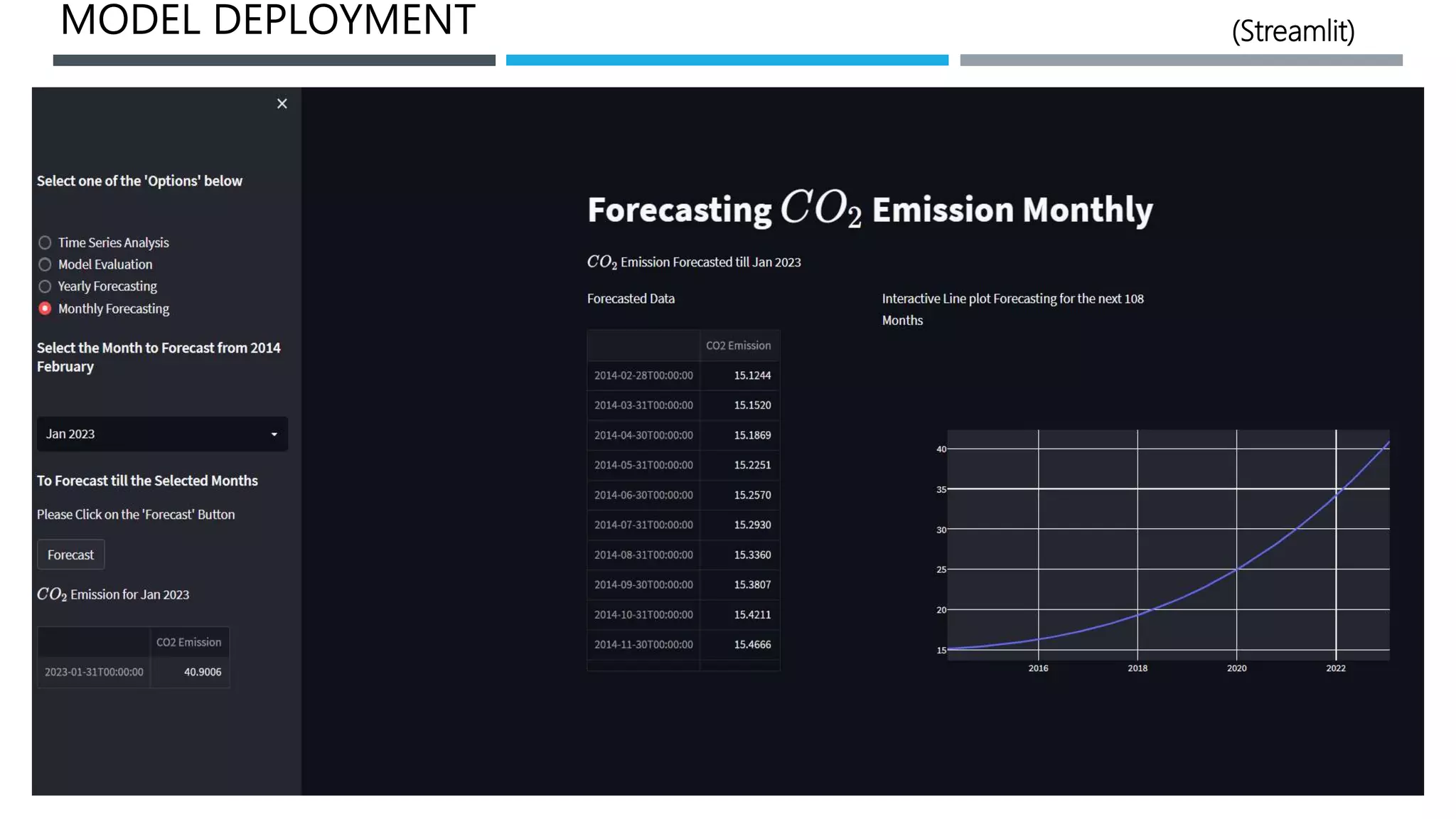
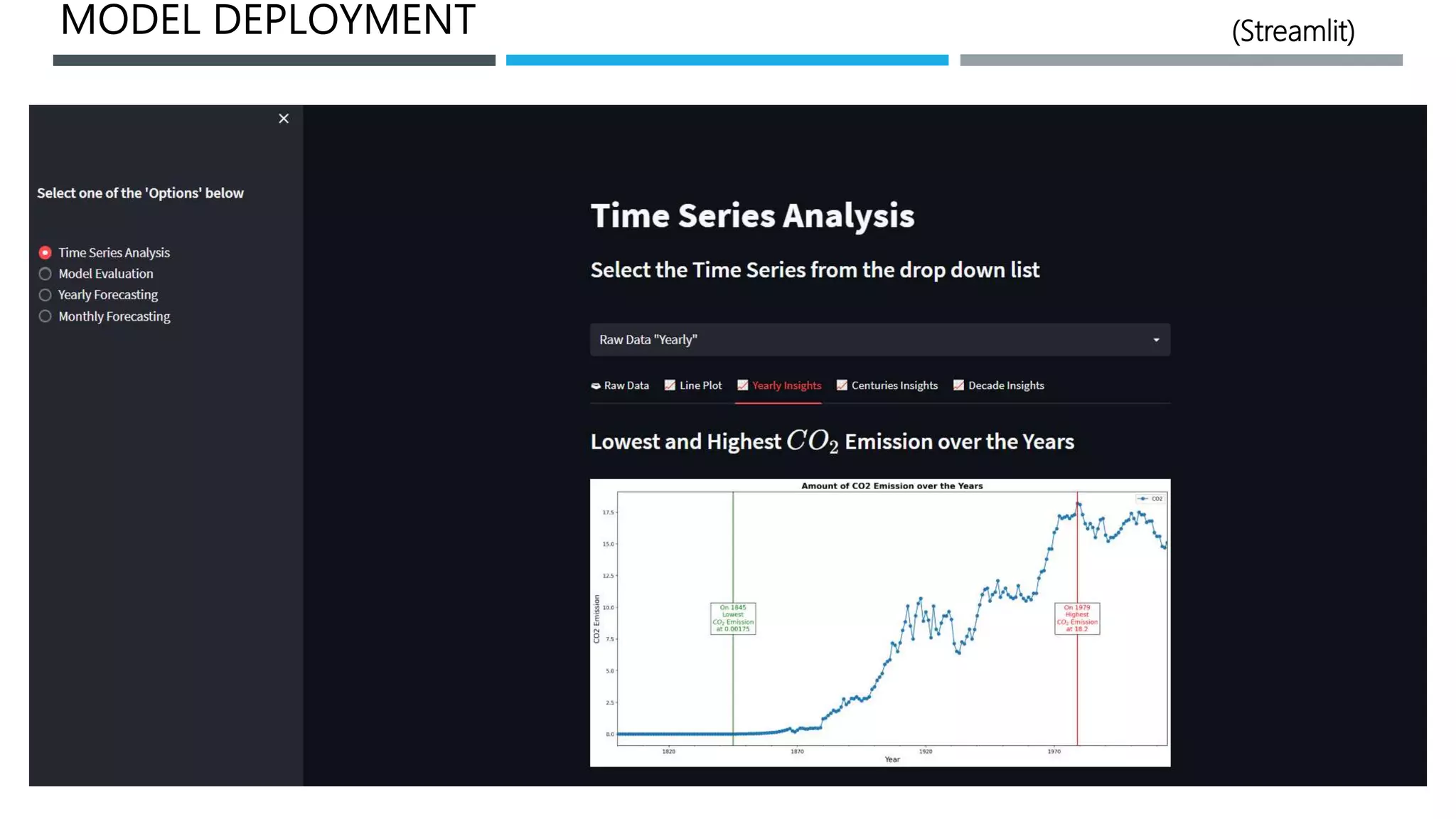
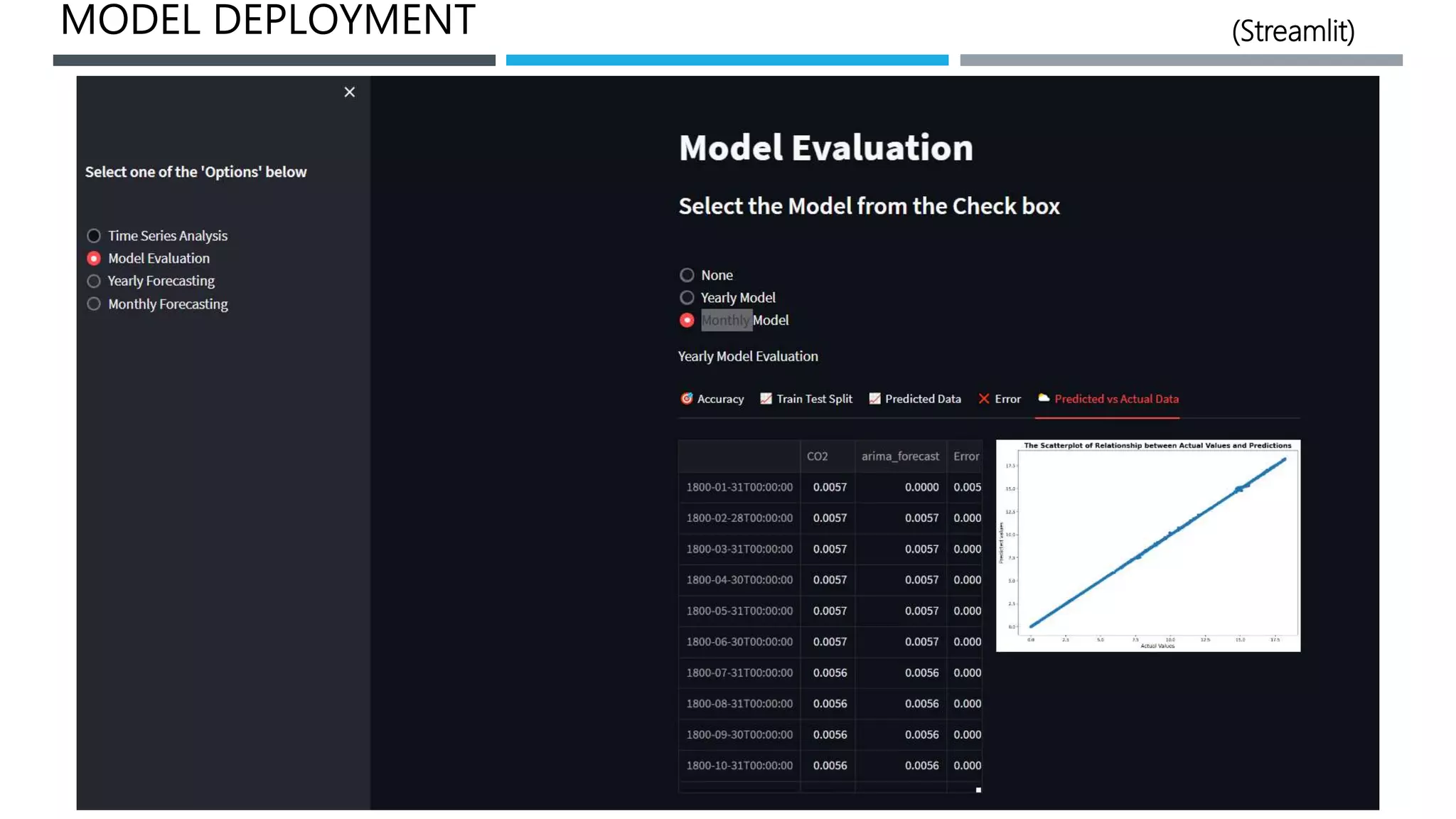
The document outlines a project to forecast CO2 emissions for an organization, ensuring compliance with government norms while addressing the significance of global warming. It details data analysis techniques, model selection criteria, and the challenges faced, such as skewed data and lack of seasonality, as well as methodologies like ARIMA and SARIMA for accurate predictions. The aim is to achieve better accuracy in short-term forecasts necessary for informed decision-making in climate change conventions.