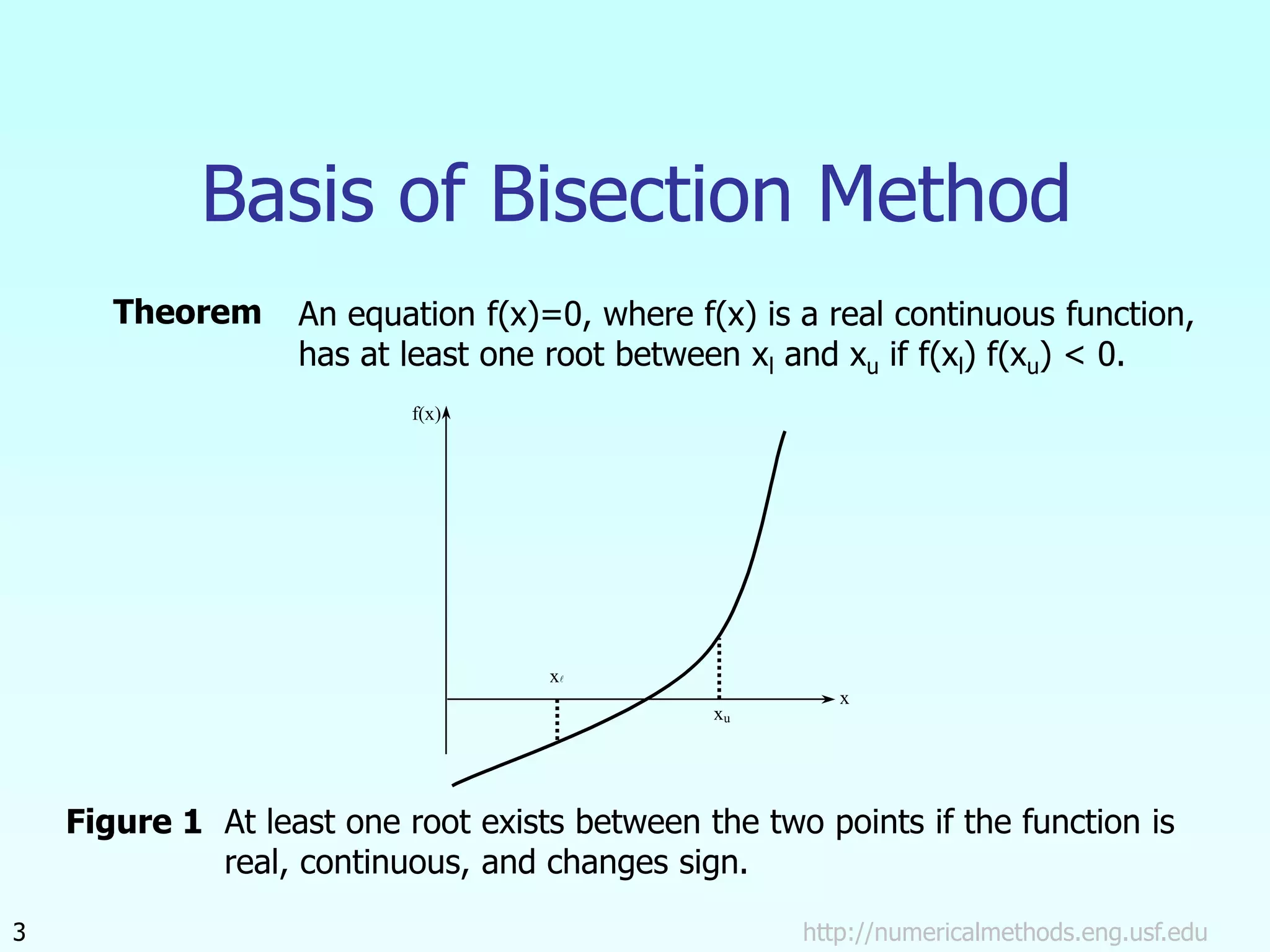
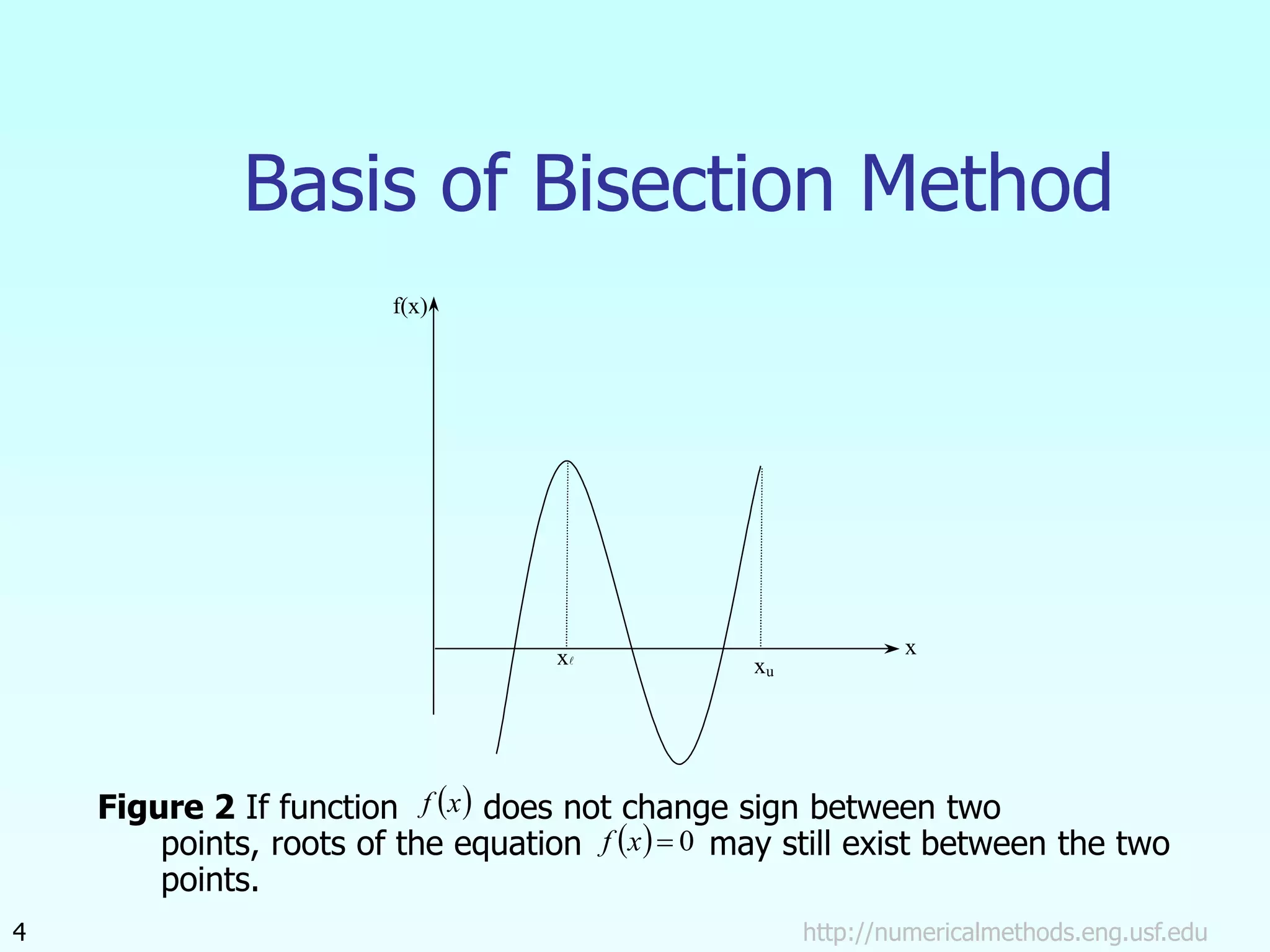
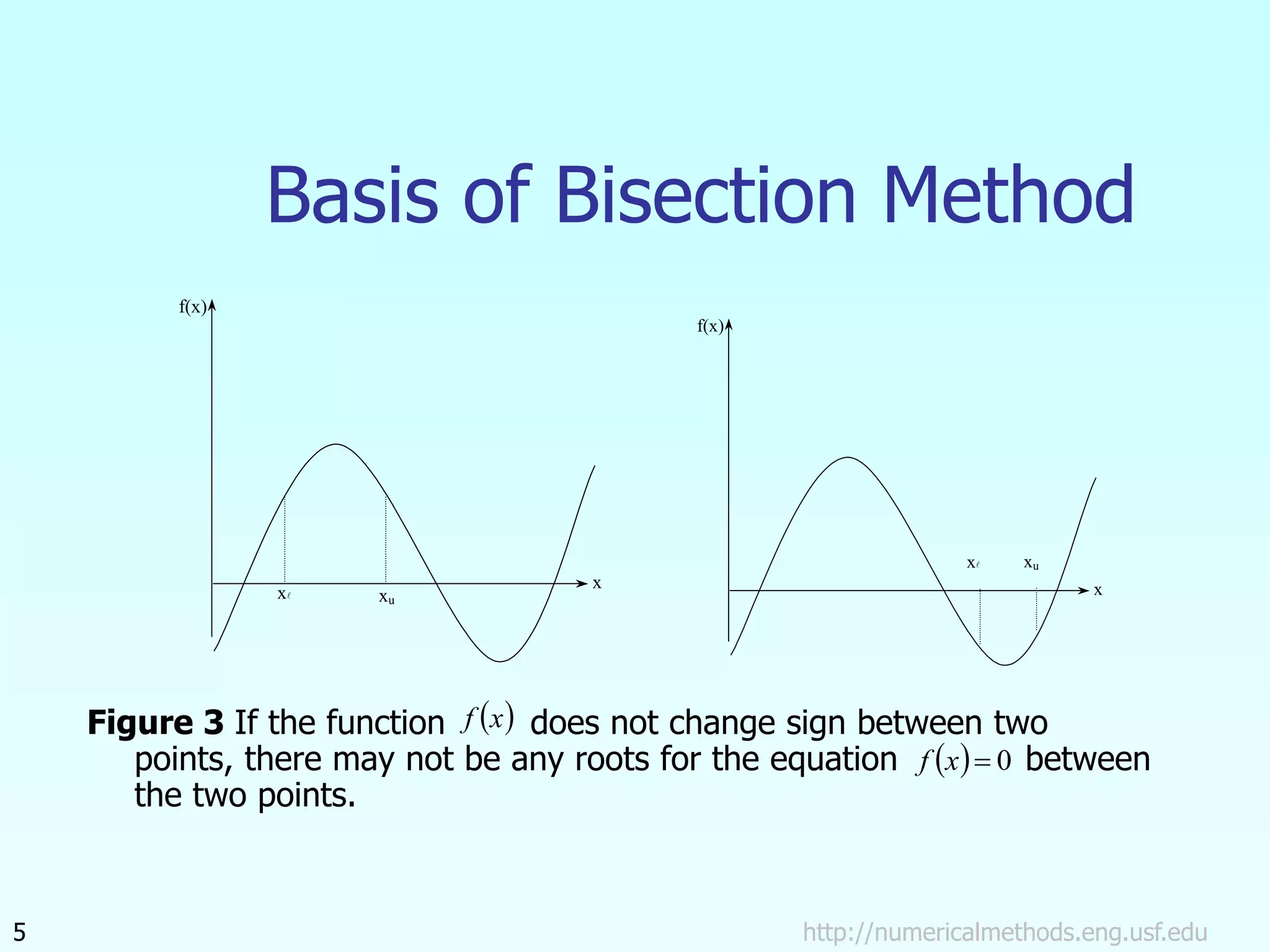
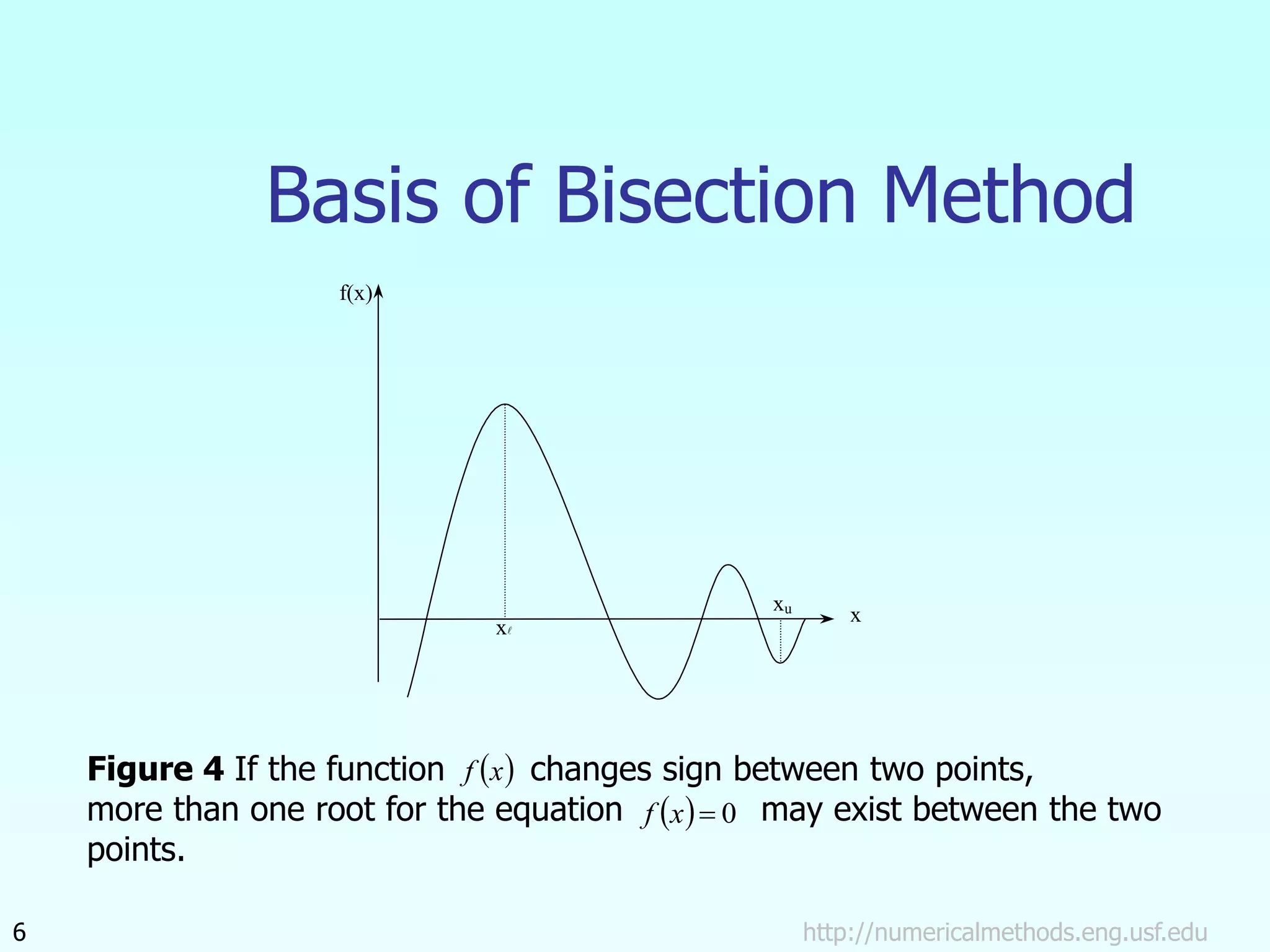
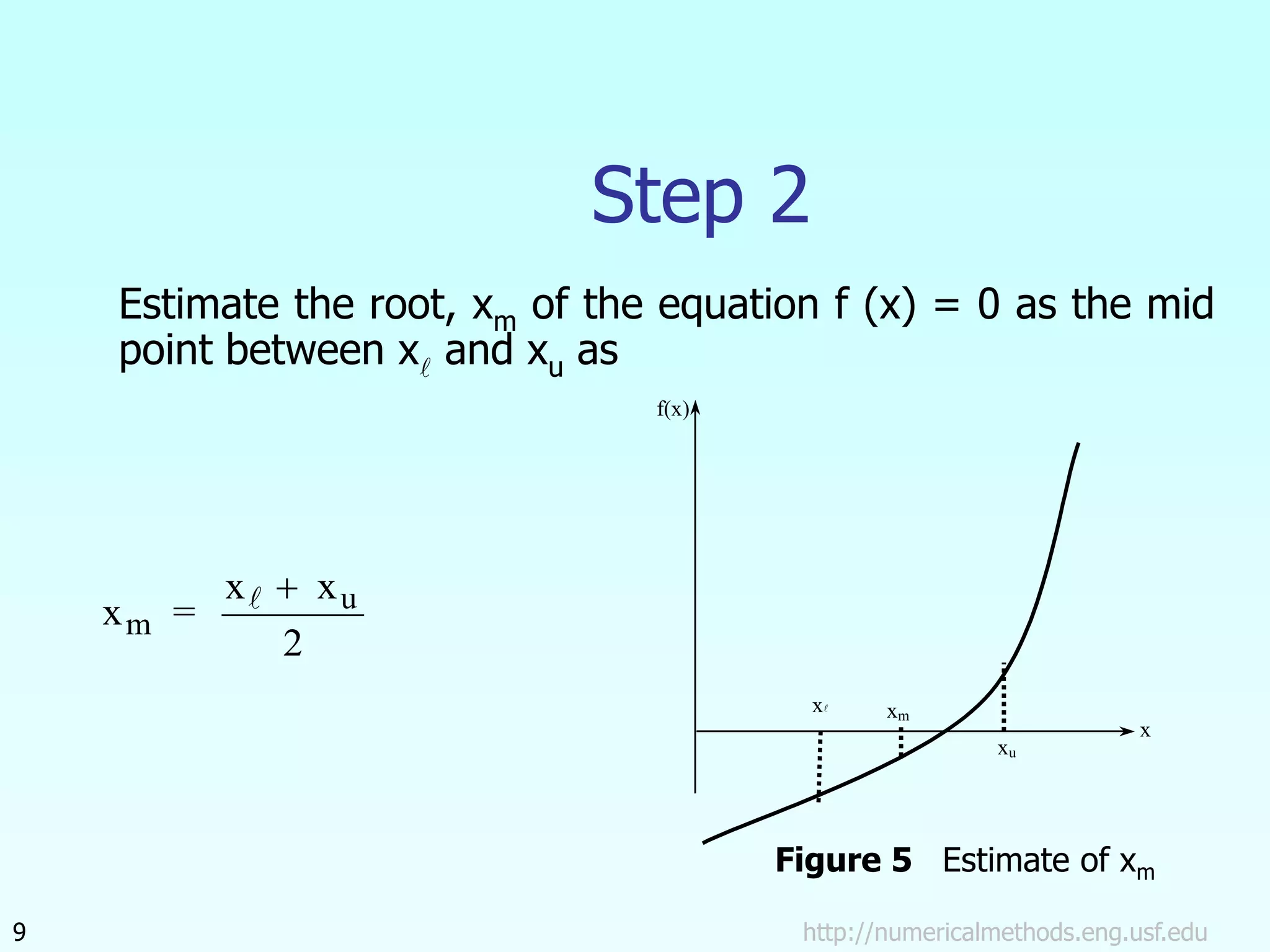
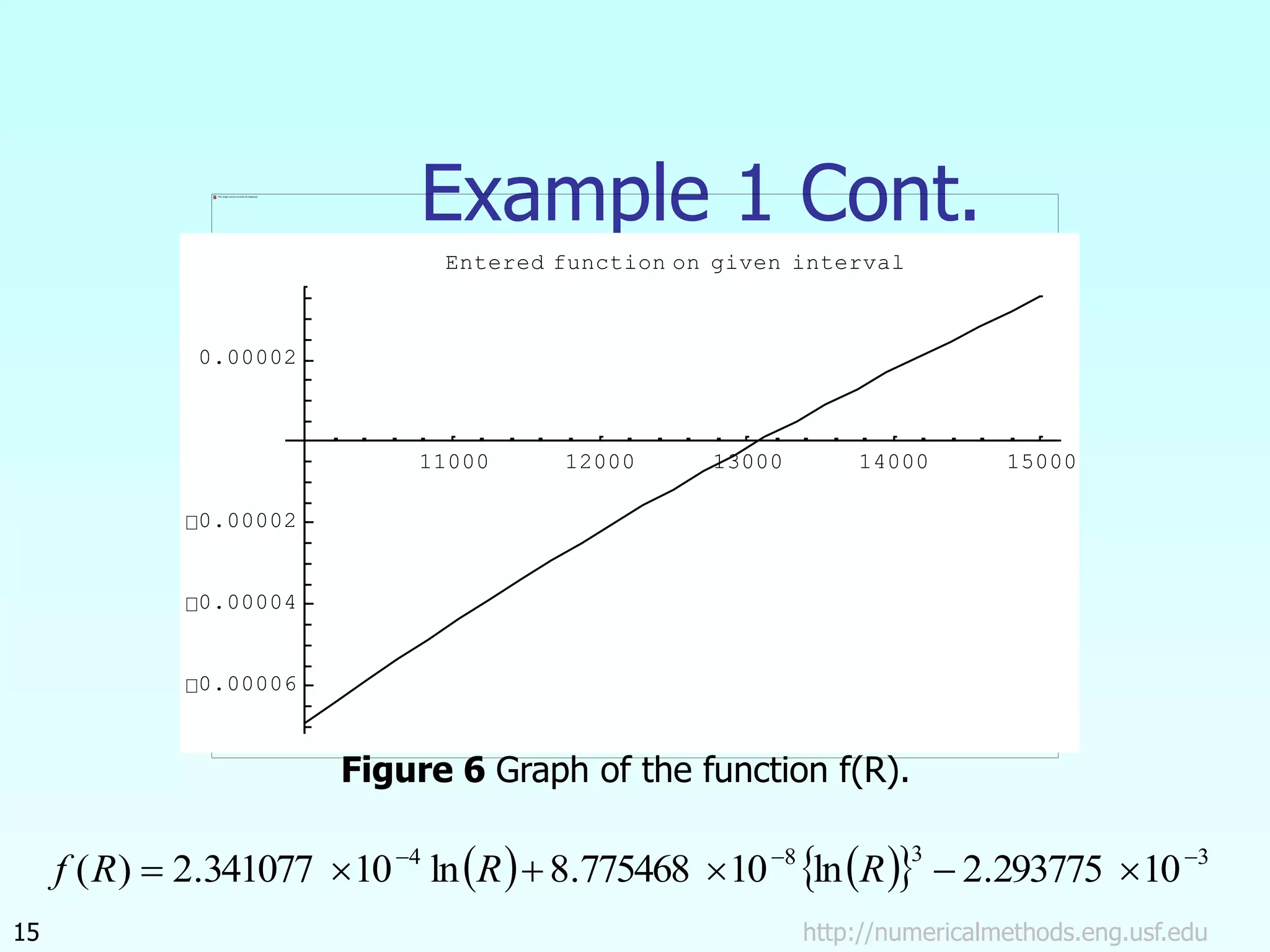
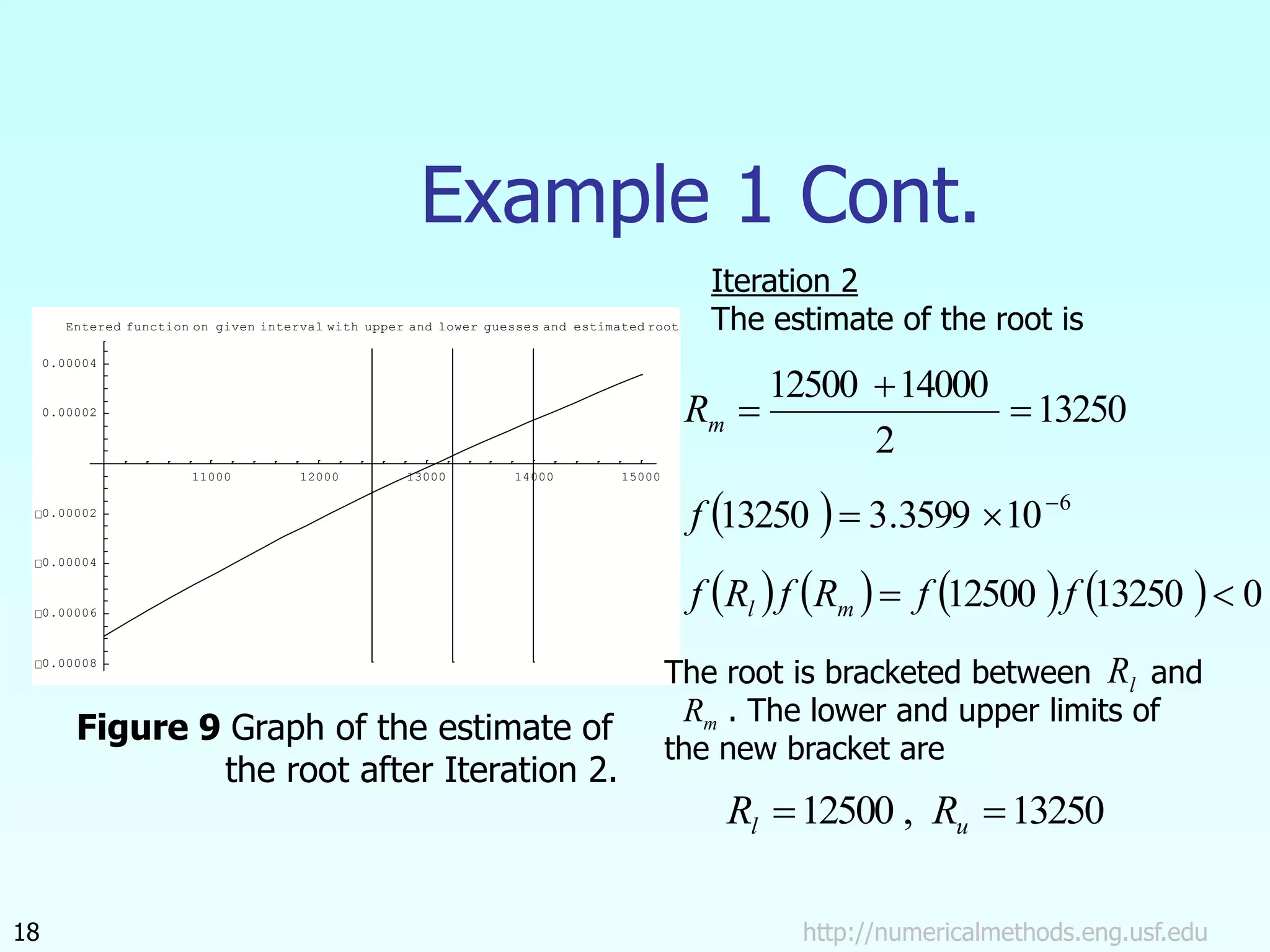
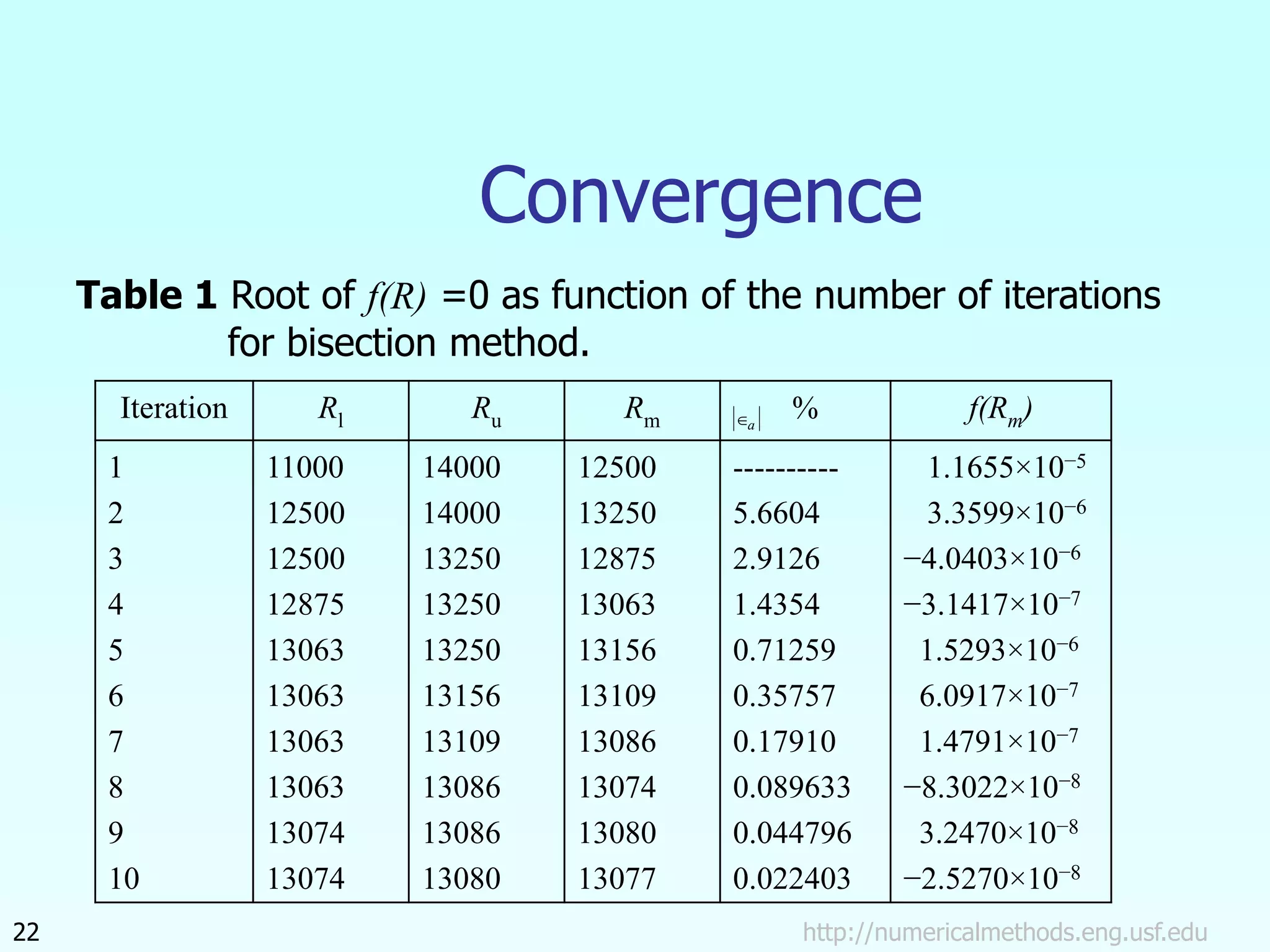
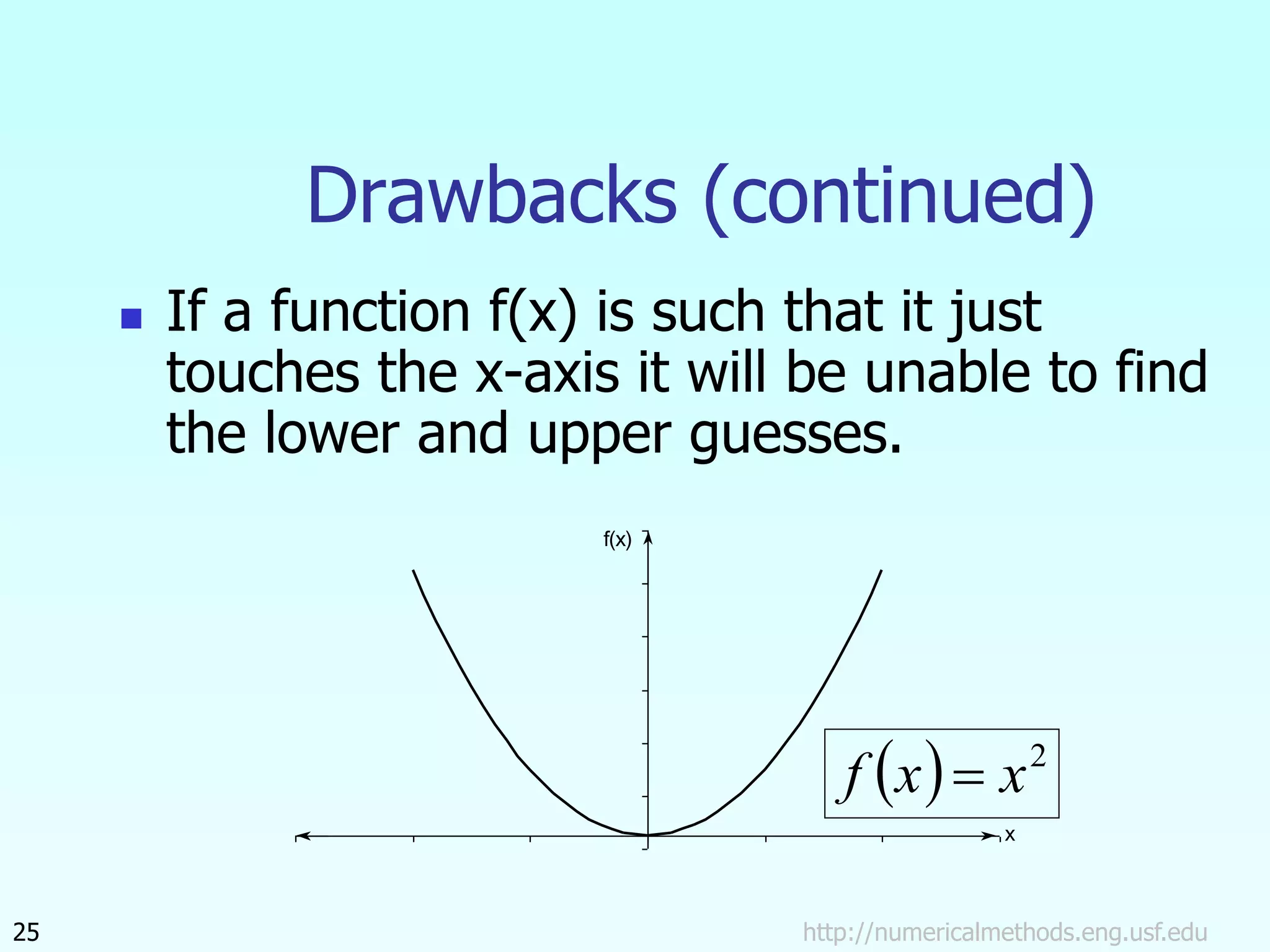
The document discusses the bisection method for finding roots of equations. It begins by outlining the basis of the bisection method, which is that if a continuous function changes sign between two points, there is a root between those points. It then provides the step-by-step algorithm for implementing the bisection method to iteratively find a root. An example application to finding the resistance of a thermistor at a given temperature is also included. The document concludes by discussing the advantages and drawbacks of the bisection method.