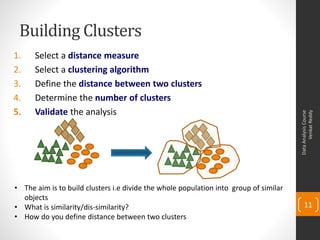
The document provides an overview of topics to be covered in a data analysis course, including cluster analysis and decision trees. The course will cover descriptive statistics, probability distributions, correlation, regression, hypothesis testing, clustering methods like k-means, and decision tree techniques like CHAID. Clustering involves grouping similar objects together to identify homogeneous clusters that are heterogeneous from each other. Applications of clustering include market segmentation, credit risk analysis, and operations. The document gives an example of clustering students based on their exam scores.