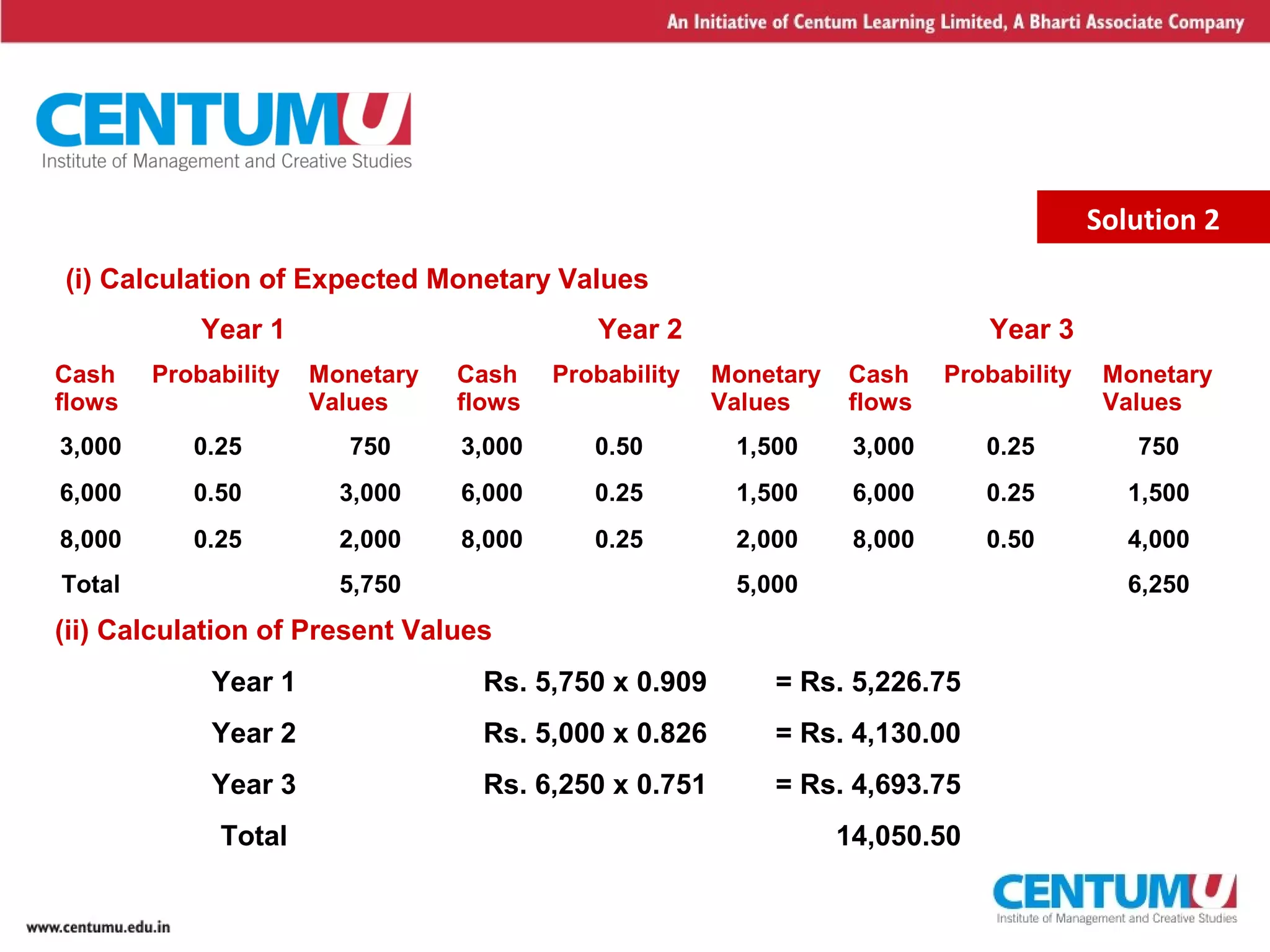
The document discusses various techniques for analyzing risk in capital budgeting decisions: - Risk refers to situations where probabilities of outcomes are known, while uncertainty refers to unknown probabilities. Risk is less variable than uncertainty. - Sensitivity analysis determines how sensitive NPV is to changes in variable assumptions by changing one variable at a time. - Scenario analysis considers multiple scenarios and their probabilities to arrive at an expected NPV. - Examples demonstrate calculating NPVs and expected returns for projects with different potential cash flows and probabilities. This provides insight into variability and risk.

2. 2
Presenting…

3. 3
Risk
The decision situations with reference to risk analysis in Capital Budgeting
Decisions can be broken up into three types (i) Risk, (ii) Uncertainty and (iii)
Certainty
Risk: The risk situation is one in which the probabilities of occurrence of a particular
event are known.
Uncertainty: The risk situation is one in which the probabilities of occurrence of a
particular event are not known.
The difference between risk and uncertainty, therefore lies in the fact that variability
is less in risk than in uncertainty.
Risk with reference to Capital Budgeting, results from the variation between the
estimated and the actual returns. The greater the variability between the two, the
more risky is the project.

4. 4
Sensitivity Analysis
Sensitivity analysis is simply the method for determining how sensitive our NPV
analysis is to changes in our variable assumptions. In this analysis, each variable is
fixed except one and by changing this one variable, the effect on NPV or IRR can be
seen. It answers “what if” questions, e.g. “What if sales decline by 30%?”
To begin a sensitivity analysis, we must first come up with a base-case scenario.
This is typically the NPV using assumptions we believe are most accurate.
From there, we can change various assumptions we had initially made based on
other potential assumptions.
NPV is then recalculated, and the sensitivity of the NPV based on the change in
assumptions is determined.
Depending on our confidence in our assumptions, we can determine how potentially
risky a project can be.

5. 5
Scenario Analysis
Scenario analysis takes sensitivity analysis a step further.
Rather than just looking at the sensitivity of our NPV analysis to changes in our
variable assumptions, scenario analysis also looks at the probability distribution of
the variables.
Like sensitivity analysis, scenario analysis starts with the construction of a base
case scenario.
From there, other scenarios are considered, known as the "best-case scenario" and
the "worst-case scenario".
Probabilities are assigned to the scenarios and computed to arrive at an expected
value.
Given its simplicity, scenario analysis is one the most frequently used risk-analysis
techniques.

6. 6
Example 1
From the under mentioned facts, compute the NPVs of the two projects for
each of the possible cash flows.
Project X (‘000 Rs.) Project Y (‘000 Rs.)
Initial Cash Outlays (t = 0) 40 40
Cash inflow estimates (t = 1-15)
Worst 6 0
Most Likely 8 8
Best 10 16
Required rate of return 0.10 0.10
Economic Life (years) 15 15

7. 7
Solution 1
The NPV of each project, assuming a 10% required rate of return, can be calculated
for each of the possible cash flows.
Expected Cash Inflows
Project X Project Y
PV NPV PV NPV
Worst Rs. 45,636 Rs. 5,636 Nil (Rs. 40,000)
Most Likely Rs. 60,848 Rs. 20,848 Rs. 60,848 Rs. 20,848
Best Rs. 76,060 Rs. 36,060 Rs. 1,21,696 Rs. 81,696
Project X is less risky than Project Y. The actual selection of the project will depend
on the decision maker’s attitude towards risk. If the decision maker is conservative,
he will select Project X as there is no possibility of suffering losses. On the other
hand if he is willing to take risks, he will choose Project Y as it has the possibility of
paying a very high return as compared to Project X.
Such analysis in spite of being crude does provide the decision maker with more
than one estimate of the project’s outcome and thus an insight into the variability of
the returns.

8. 8
Probability
Assigning probability to expected cash flows provides a more precise measure of
the variability of cash flows. The concept of probability is helpful as it indicates the
percentage chance of occurrence of each possible cash flow.
For instance, if some expected cash flow has 0.6 probability of occurrence, it means
that the given cash flow is likely to be obtained in 6 out of 10 times. Likewise if a
cash flow has a probability of 1, it is certain to occur.
Probability helps in estimating the expected return on the project.
The expected value of a project is a weighted average return, where the weights are
the probabilities assigned to the various expected events, that is the expected
monetary values of the estimated cash flows multiplied by the probabilities.

9. 9
Example 2
Year 1 Year 2 Year 3
Cash flows Probability Cash flows Probability Cash flows Probability
Rs. 3,000 0.25 Rs. 3,000 0.50 Rs. 3,000 0.25
Rs. 6,000 0.50 Rs. 6,000 0.25 Rs. 6,000 0.25
Rs. 8,000 0.25 Rs. 8,000 0.25 Rs. 8,000 0.50
The following information is available regarding the expected cash flows generated,
and their probability for Company X. What is the expected return on the project?
Assuming 10% as the discount rate, find out the present values of the expected
monetary values.

10. 10
Solution 2
Year 1 Year 2 Year 3
Cash
flows
Probability Monetary
Values
Cash
flows
Probability Monetary
Values
Cash
flows
Probability Monetary
Values
3,000 0.25 750 3,000 0.50 1,500 3,000 0.25 750
6,000 0.50 3,000 6,000 0.25 1,500 6,000 0.25 1,500
8,000 0.25 2,000 8,000 0.25 2,000 8,000 0.50 4,000
Total 5,750 5,000 6,250
(i) Calculation of Expected Monetary Values
(ii) Calculation of Present Values
Year 1 Rs. 5,750 x 0.909 = Rs. 5,226.75
Year 2 Rs. 5,000 x 0.826 = Rs. 4,130.00
Year 3 Rs. 6,250 x 0.751 = Rs. 4,693.75
Total 14,050.50

11. 11
Example 3
State Probability Rate of Return
Security A Security B
Recession 0.20 -0.15 0.20
Normal 0.50 0.20 0.30
Boom 0.30 0.60 0.40
The following are the different states of economy, the probability of occurrence of
that state and the expected rate of return from Security A and B in these different
states.
Find out the expected returns and the standard deviations for these two securities.
Suppose an investor has Rs. 20,000 to invest. He invests Rs. 15,000 in security A and
balance in Security B, what will be the expected return and the standard deviation of
the portfolio?

12. 12
The expected returns RA and RB are just the possible returns multiplied by the
associated probabilities as follows:
RA = (0.20 x – 0.15) + (0.50 x 0.20) + (0.30 x 0.60)
= 25 %
RB = (0.20 x 0.20) + (0.50 x 0.30) + (0.30 x 0.40)
= 31 %
The standard deviations can now be calculated as follows:
σA = [0.20 (- 0.15 – 0.25)2
+ 0.50 (0.20 – 0.25)2
+ 0.30 (0.60 – 0.25)2
]1/2
= (0.0700)1/2
= 26.46 %
σB = [0.20 (0.20 – 0.31)2
+ 0.50 (0.30 – 0.31)2
+ 0.30 (0.40 – 0.31)2
]1/2
= (0.0049)1/2
= 7 %
Solution 3
The expected return and standard deviation of the portfolio of the
investor are:
Expected return = (0.75 x 0.25) + (0.25 x 0.31) = 26.5 %
Continued….

13. 13
Solution 3
Note: As the investor is investing Rs. 15,000 in A and Rs. 5000 in B, his portfolio will
consist of 0.75 of A and 0. 25 of B.
State Probability Expected Return
Recession 0.20 (0.75 x – 0.15) + (0.25 x 0.20) = - 0.0625
Normal 0.50 (0.75 x 0.20) + (0.25 x 0.30) = 0.2250
Boom 0.30 (0.75 x 0.60) + (0.25 x 0.40) = 0.5500
Expected Return = (0.20 x – 0.0625) + (0.50 x 0.2250) + (0.30 x 0.5500)
= 26.5 %
The standard deviation of the portfolio is:
σ = [0.20 (- 0.0625-0.265)2
+ 0.50(0.225 – 0.265)2
+ 0.30(0.550 – 0.265)2
]1/2
= [0.0466]1/2
= 21.59%
Alternatively, expected return and standard deviation can also be found by:

14. 14
QUESTIONS ?QUESTIONS ?

15. 15
Thank you
Centum U – Institute of Management & Creative Studies
37 Link Road, Lajpat Nagar,
New Delhi-110024
Tel: 91-11-46120700-04, Toll Free: 1800-103-4457
E-mail: singh_rana@yahoo.com