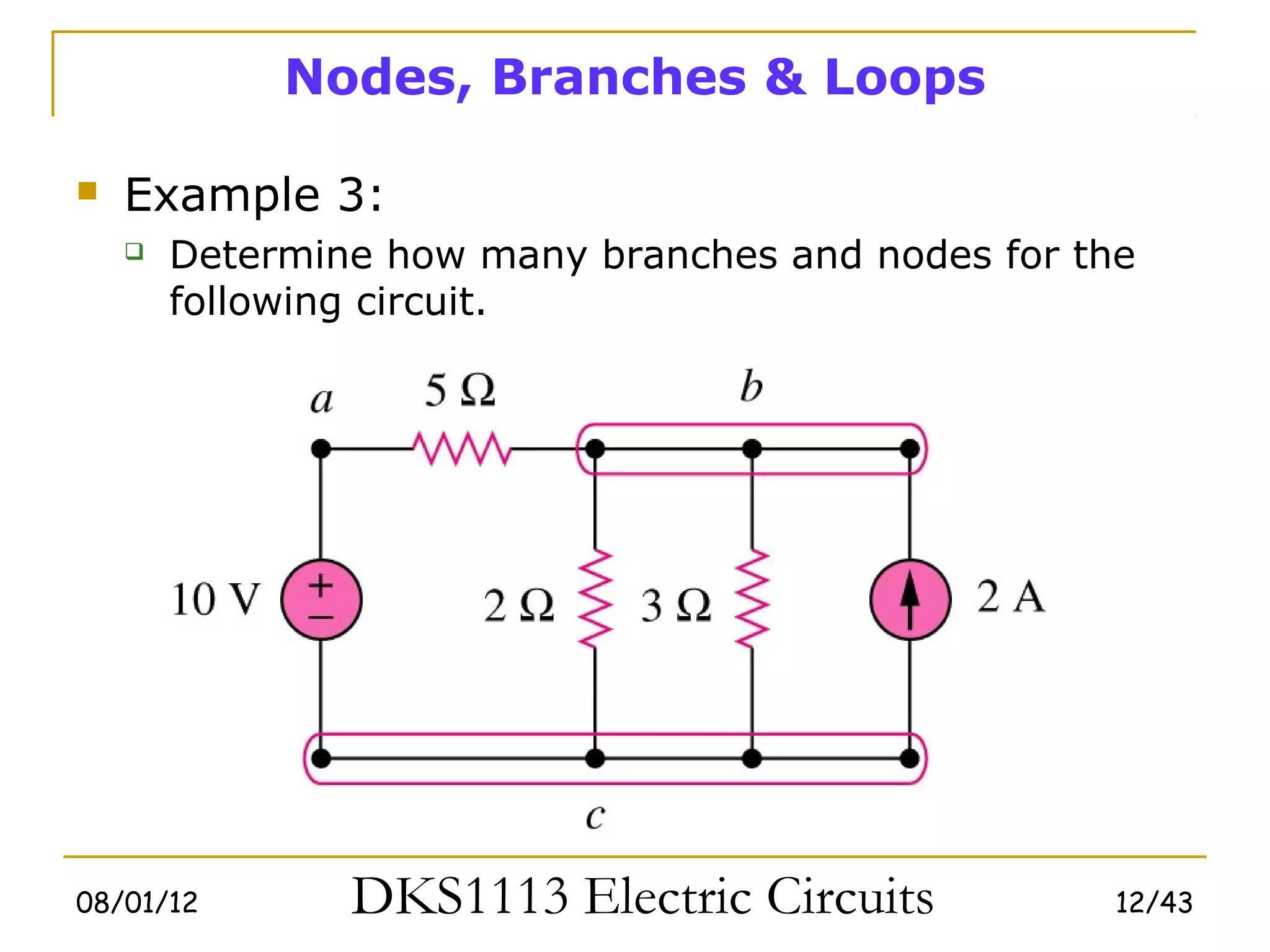
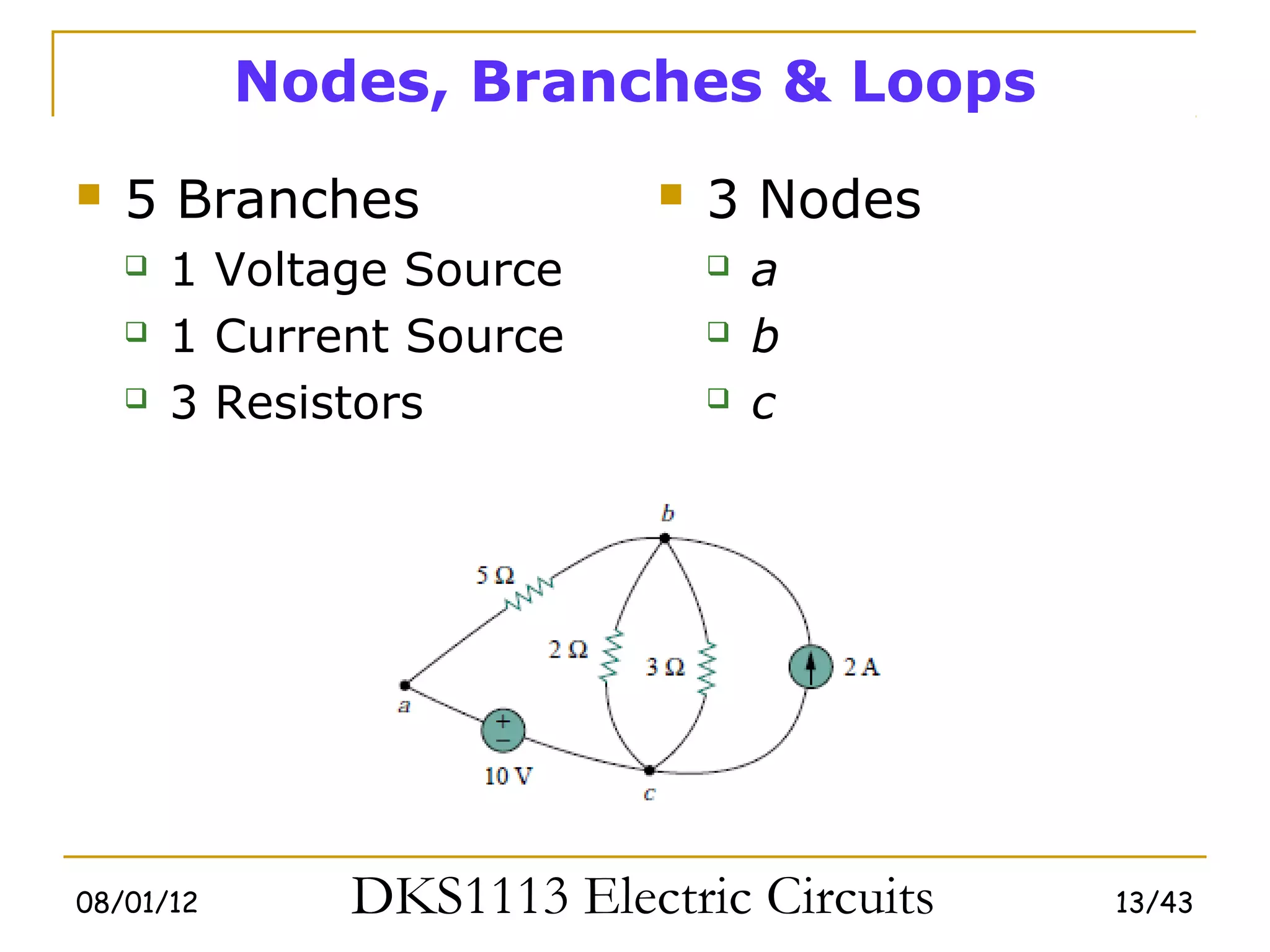
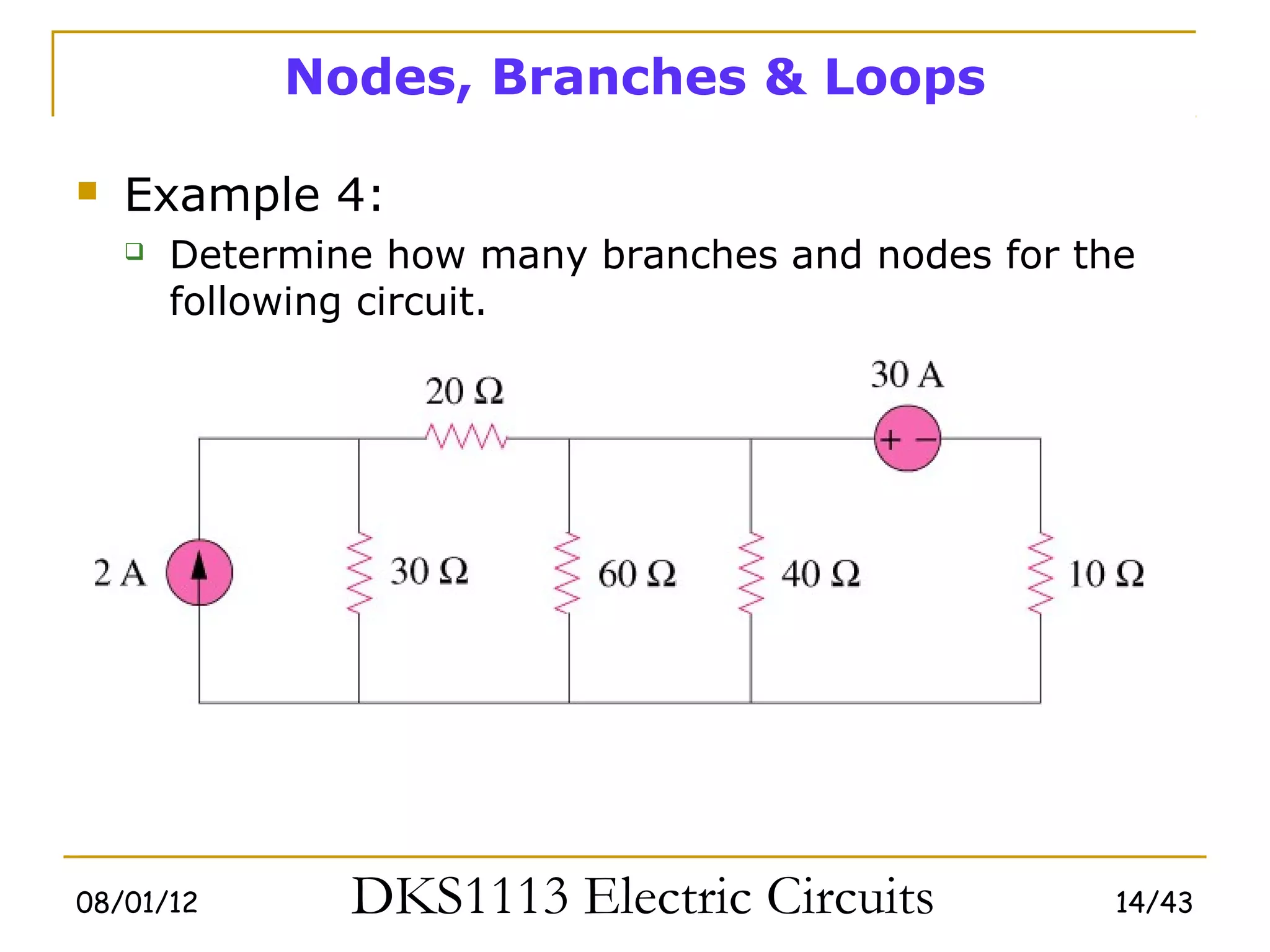
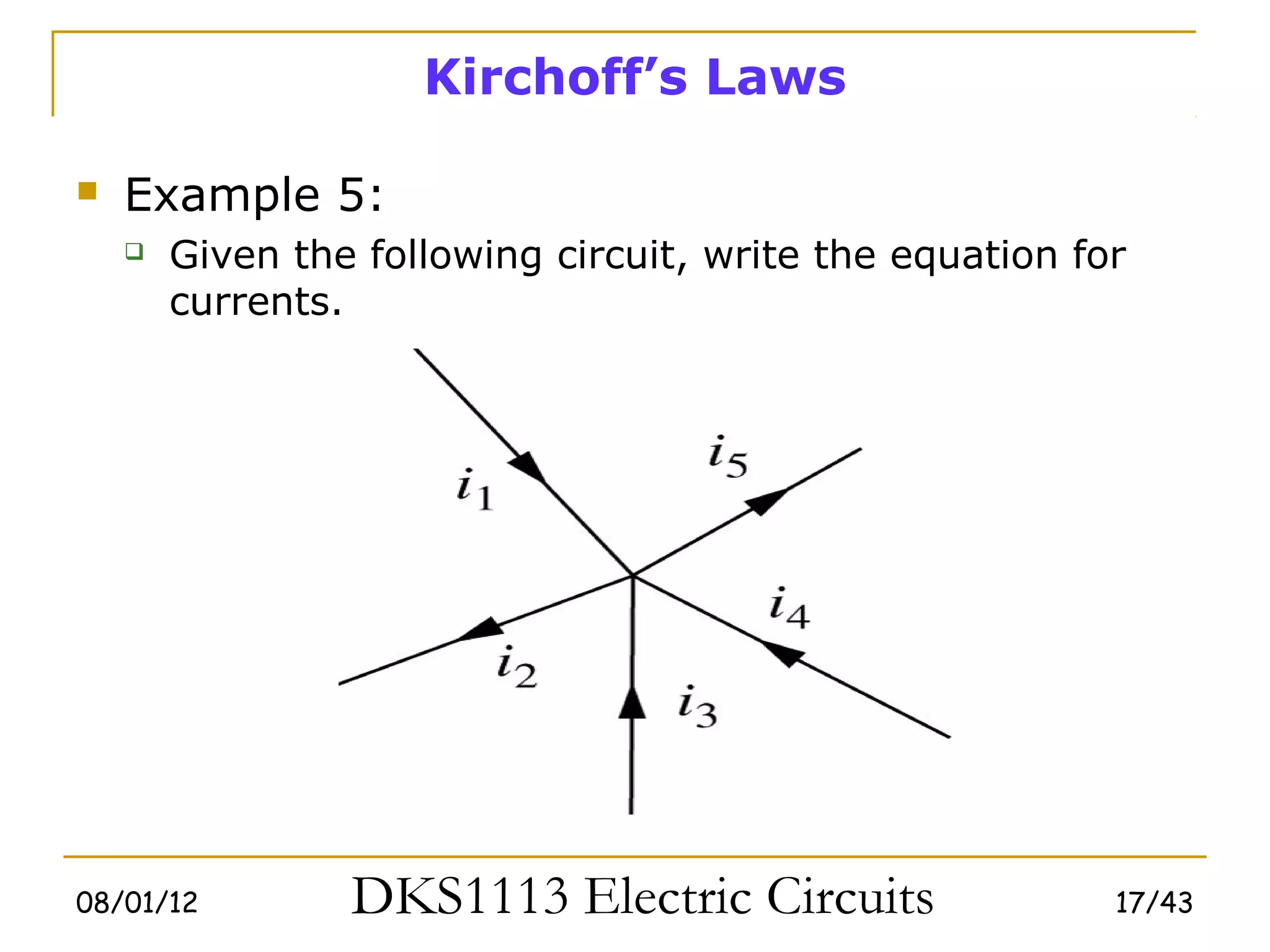
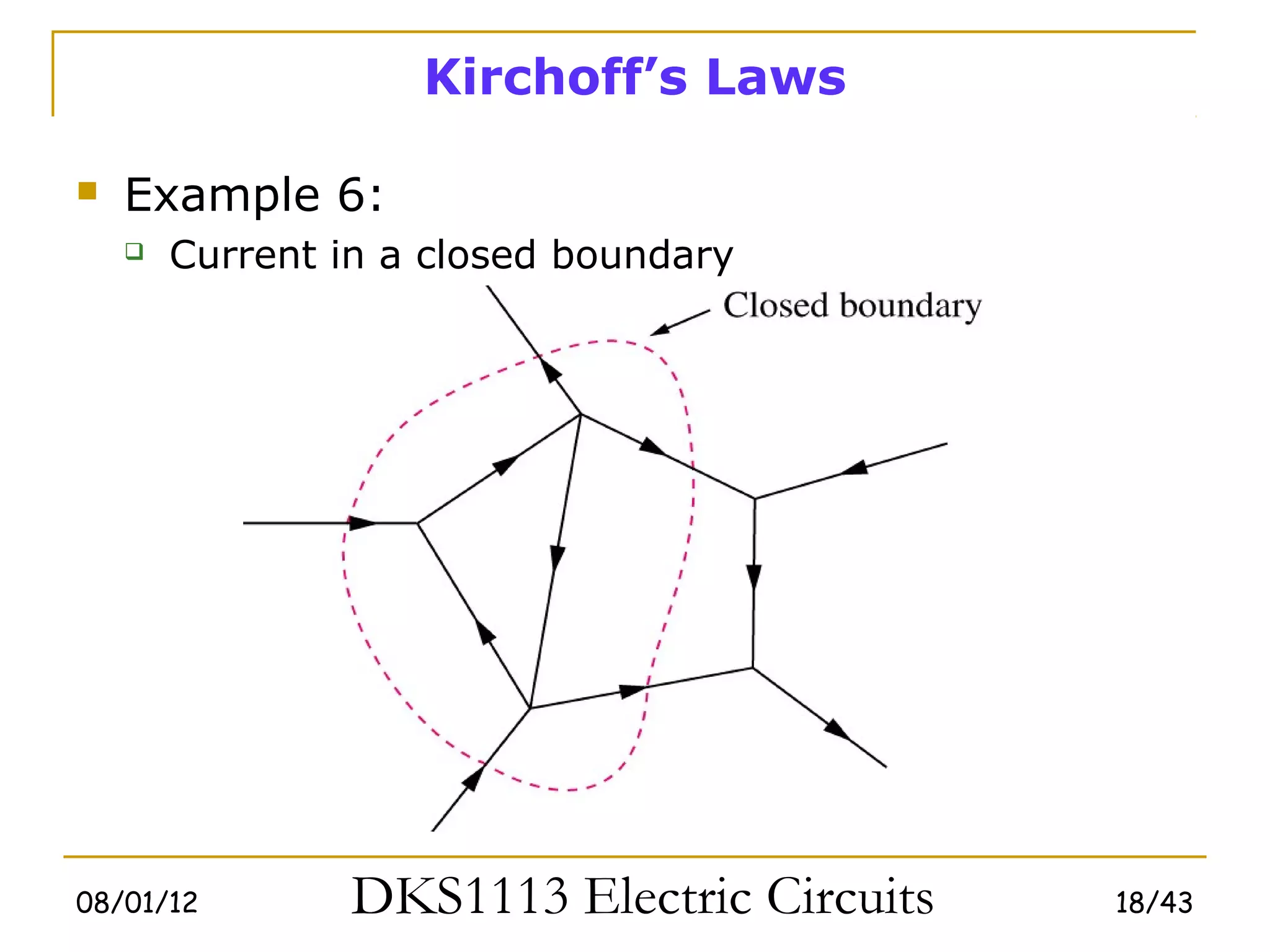
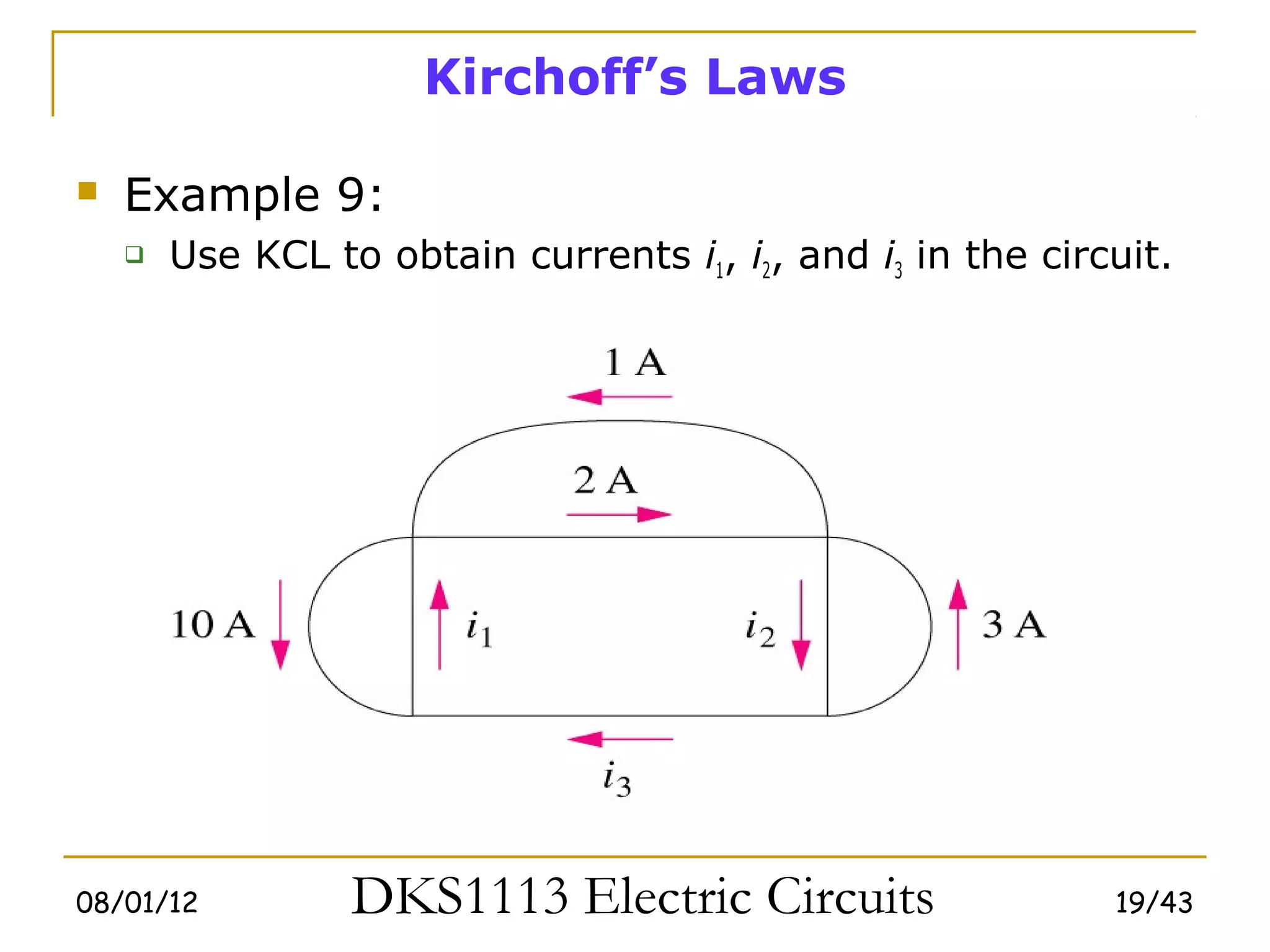
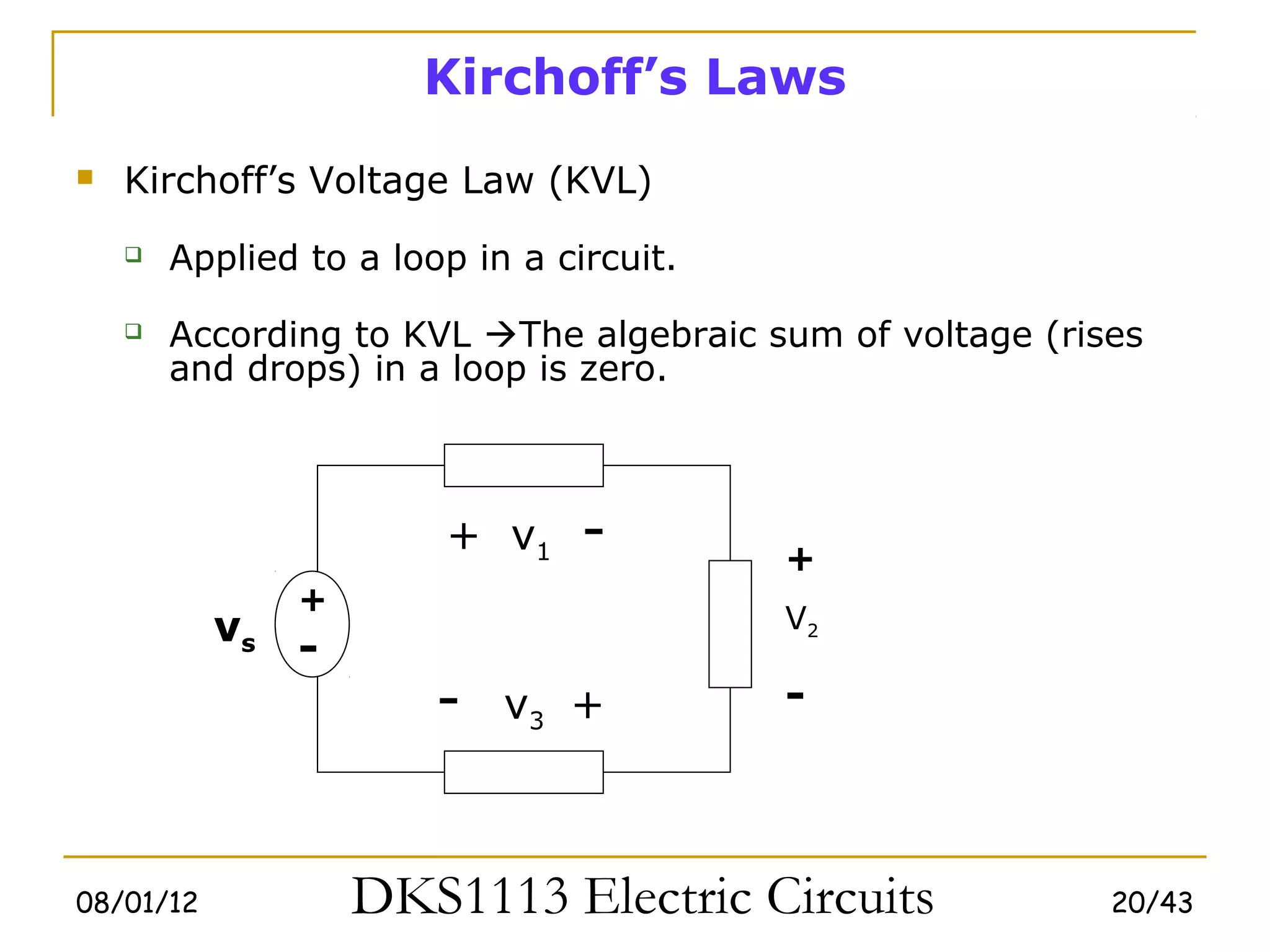
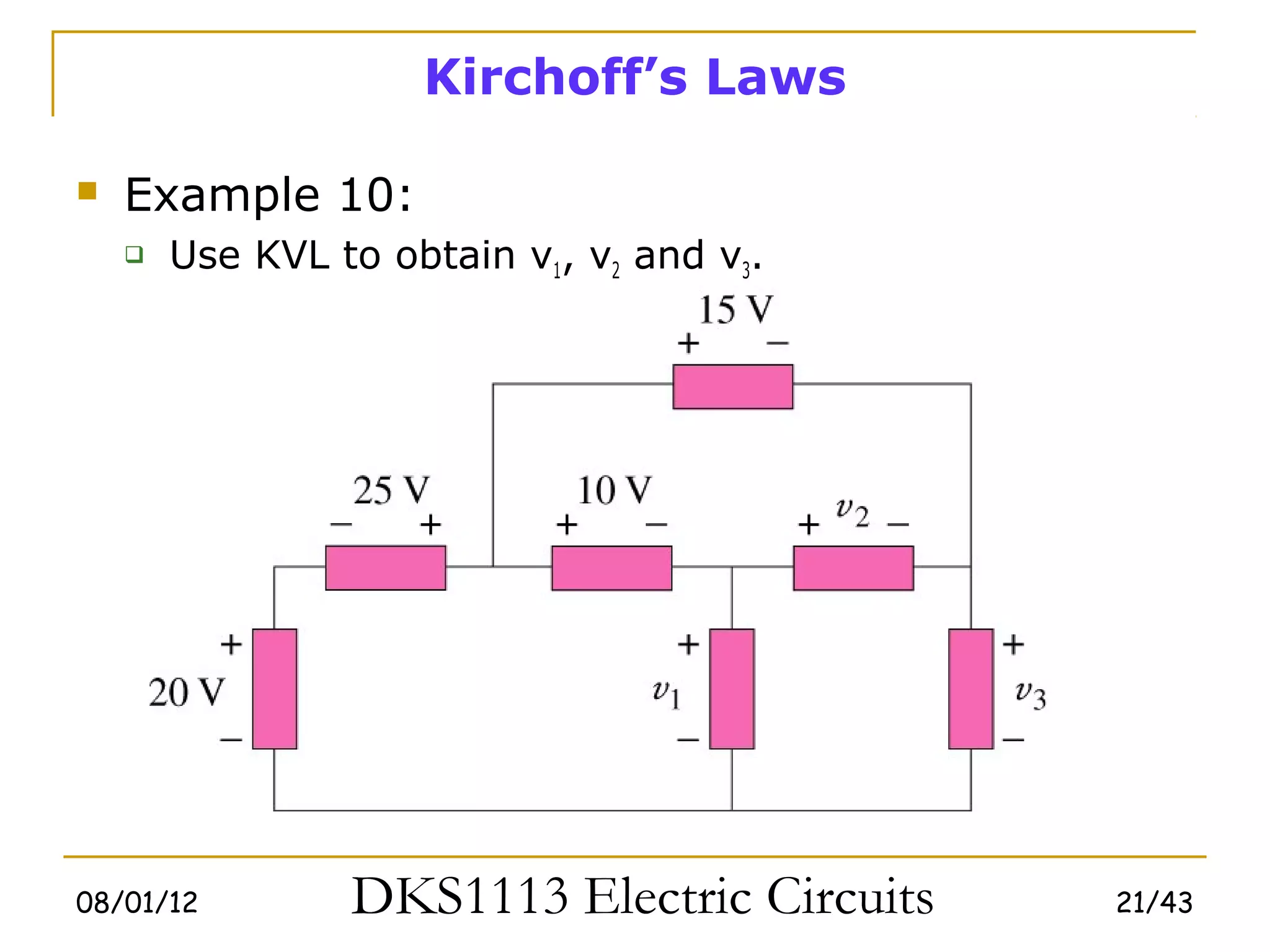
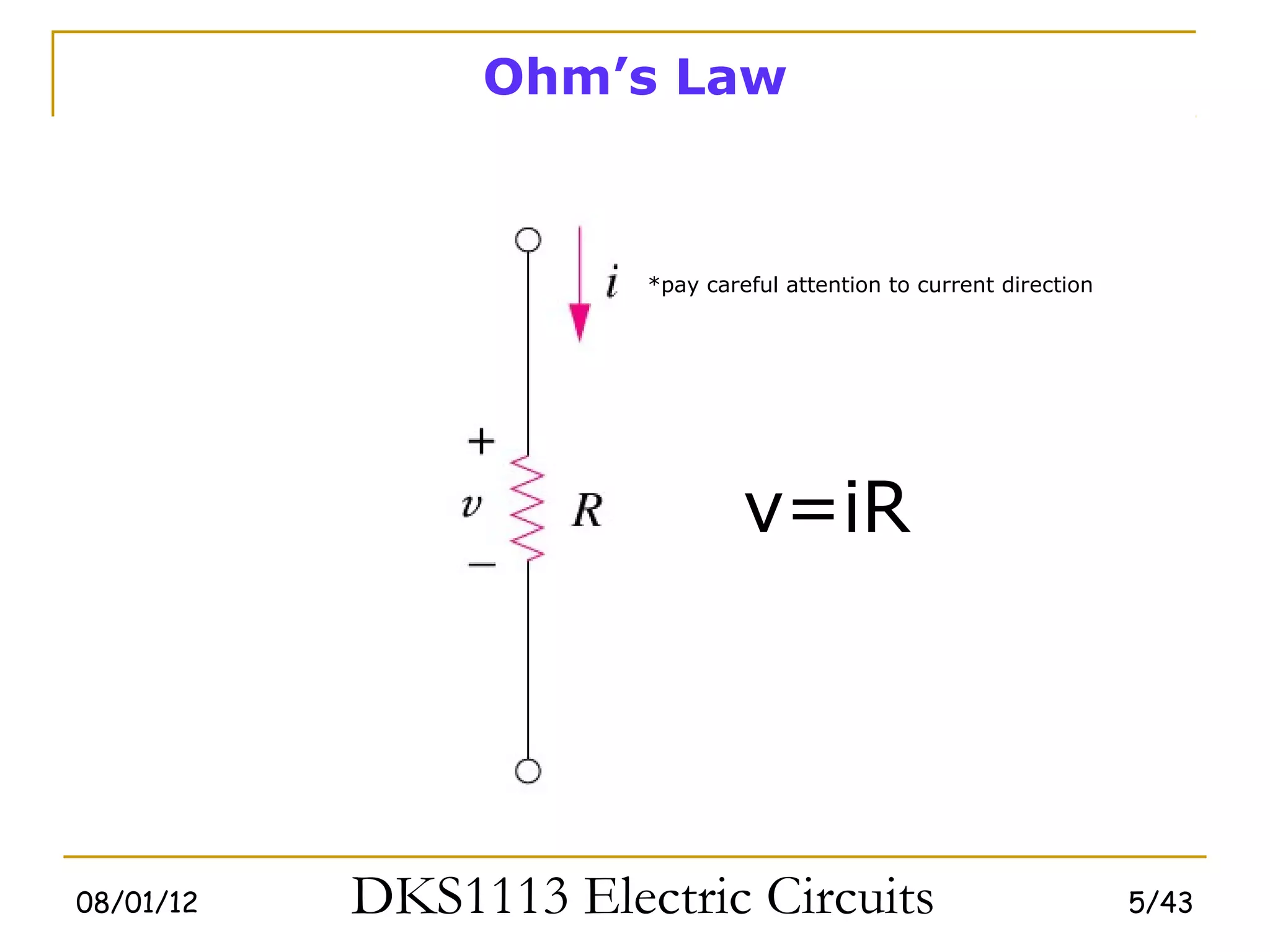
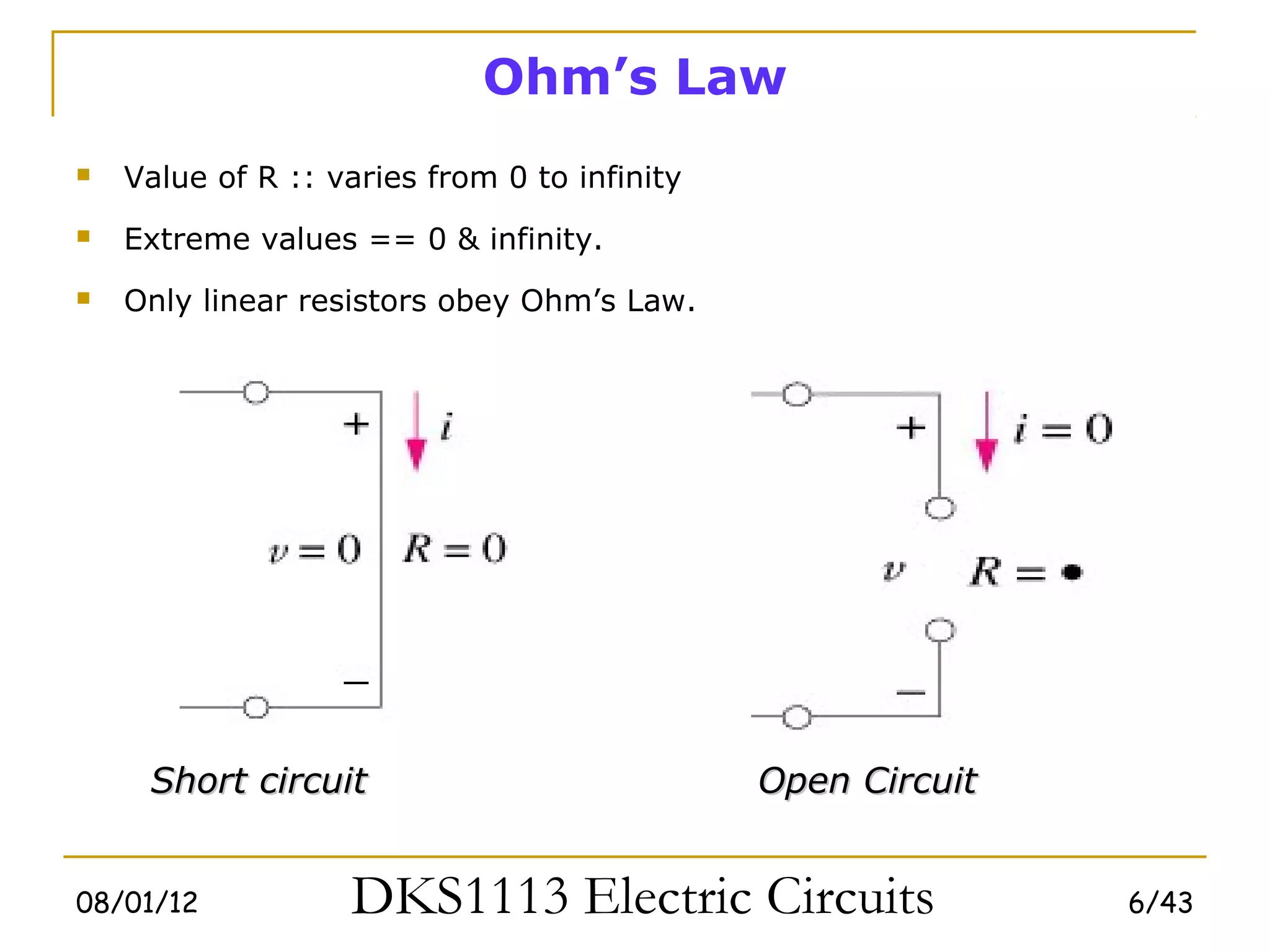
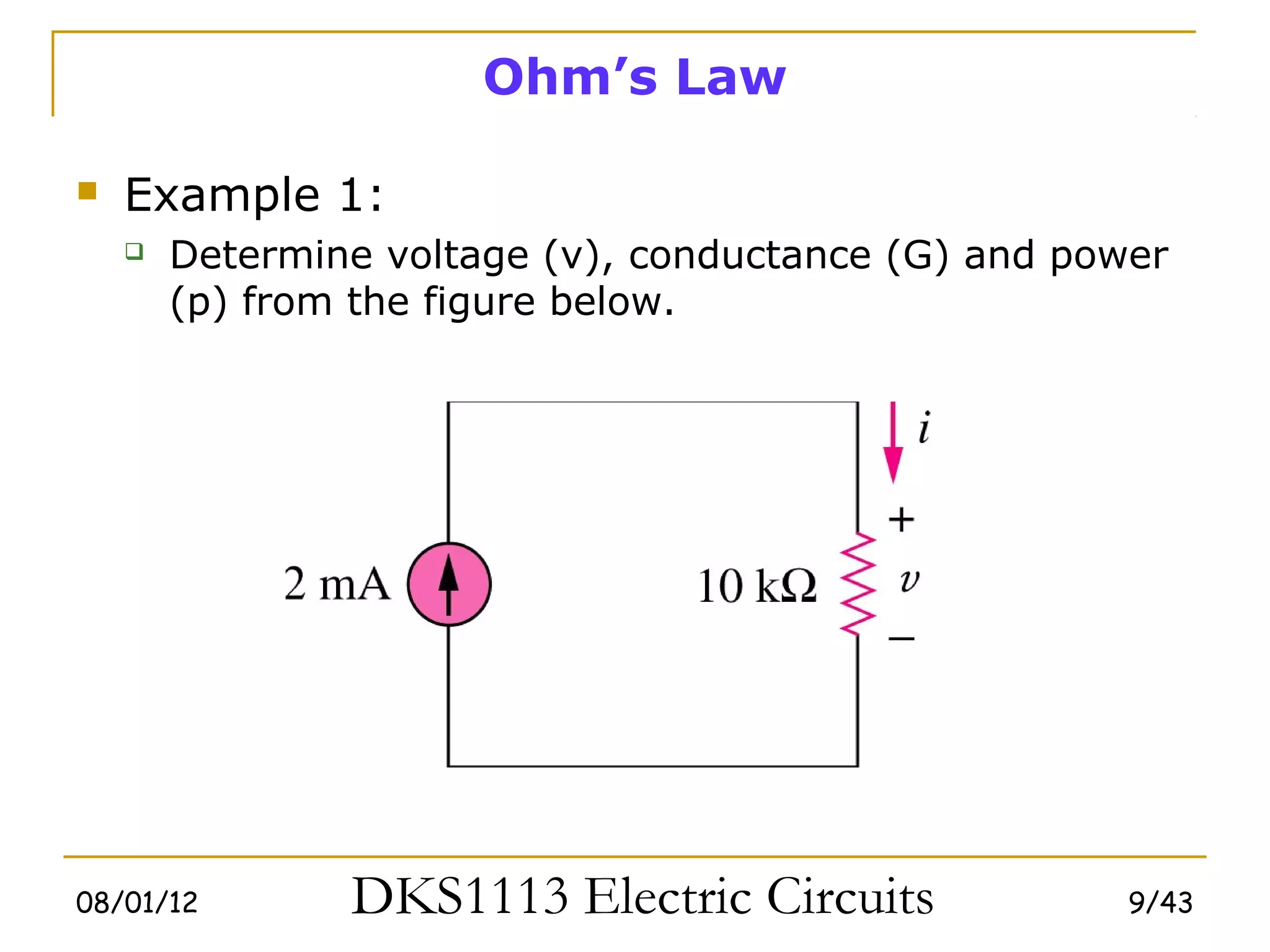
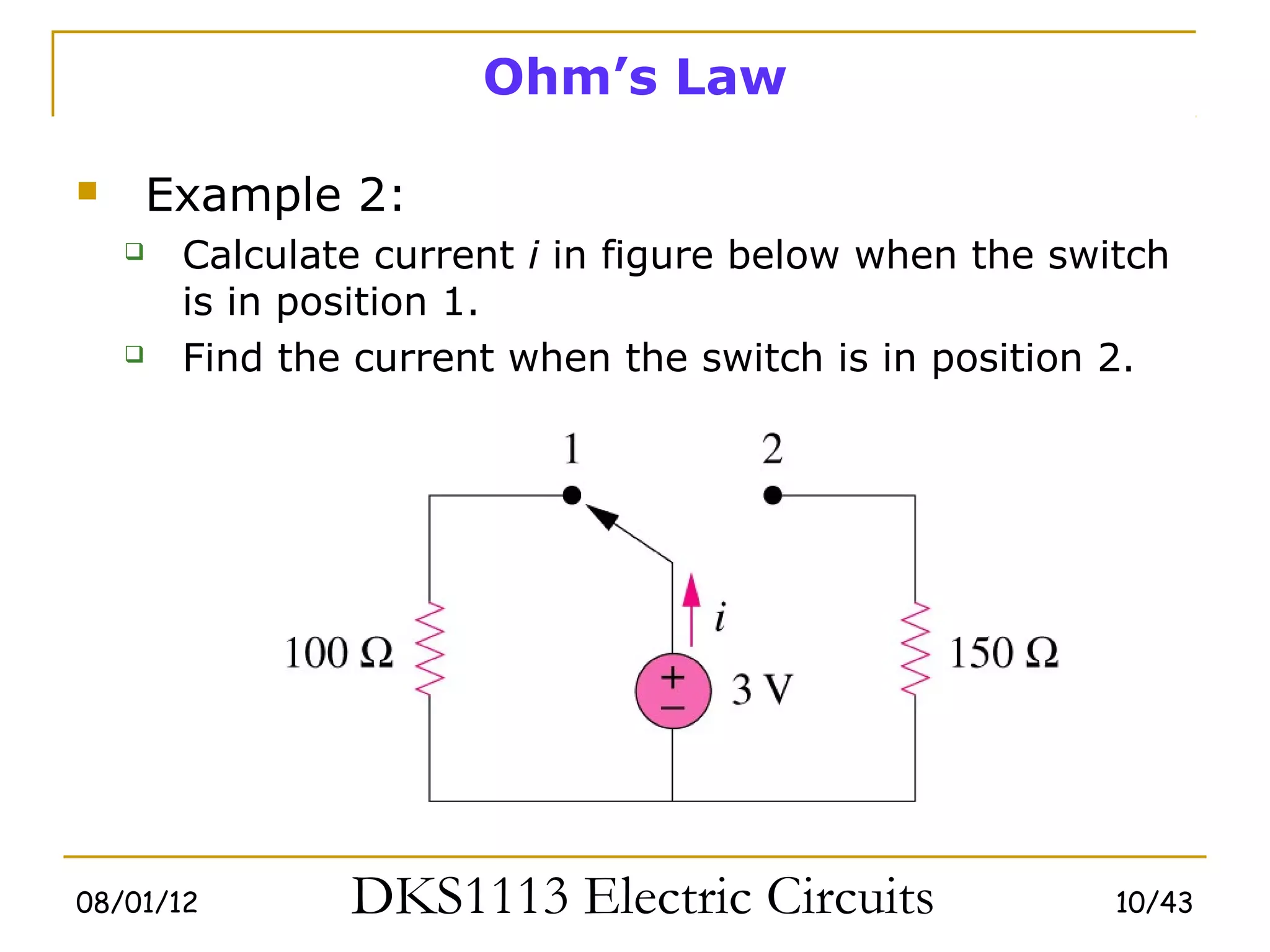
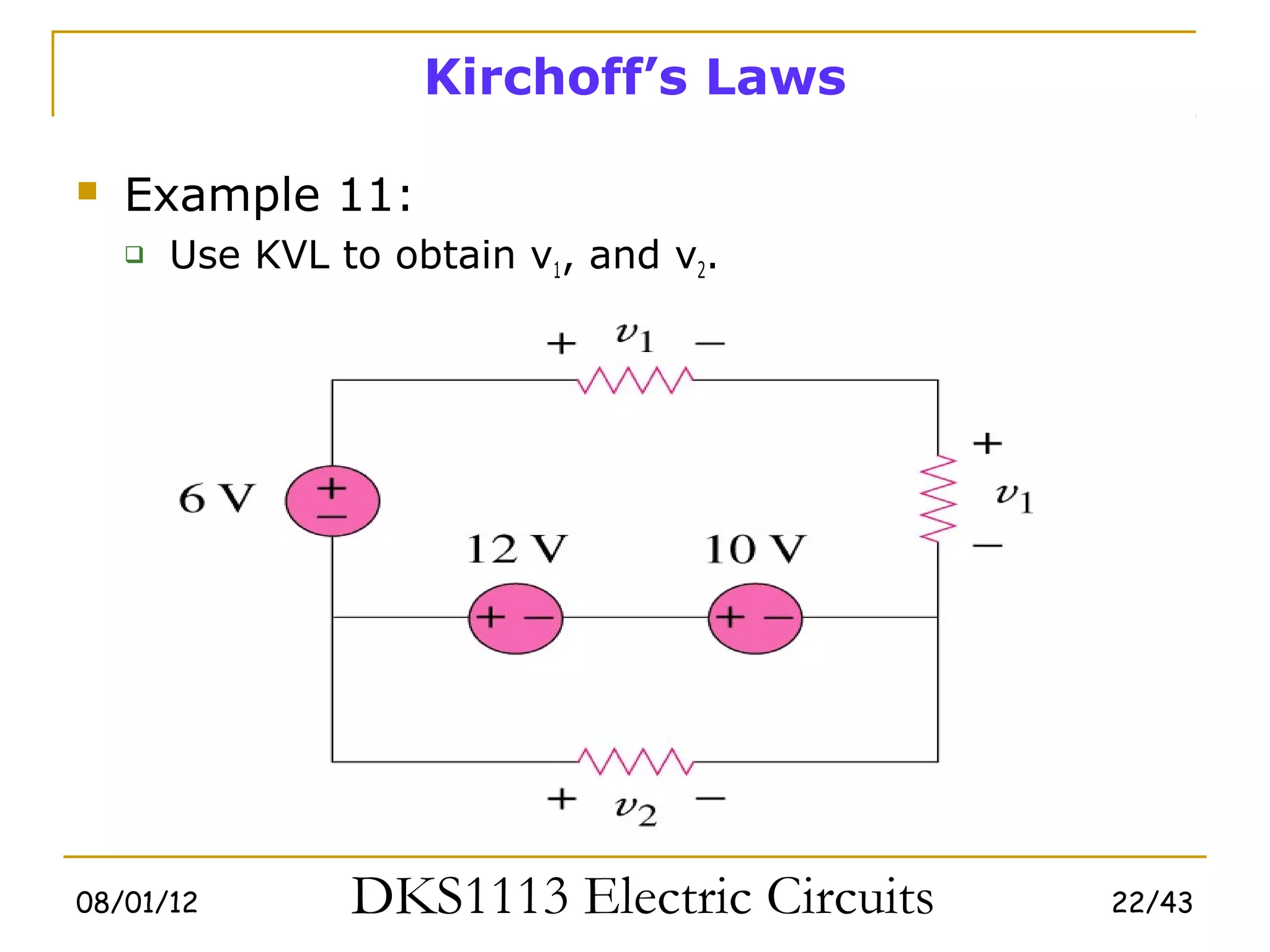
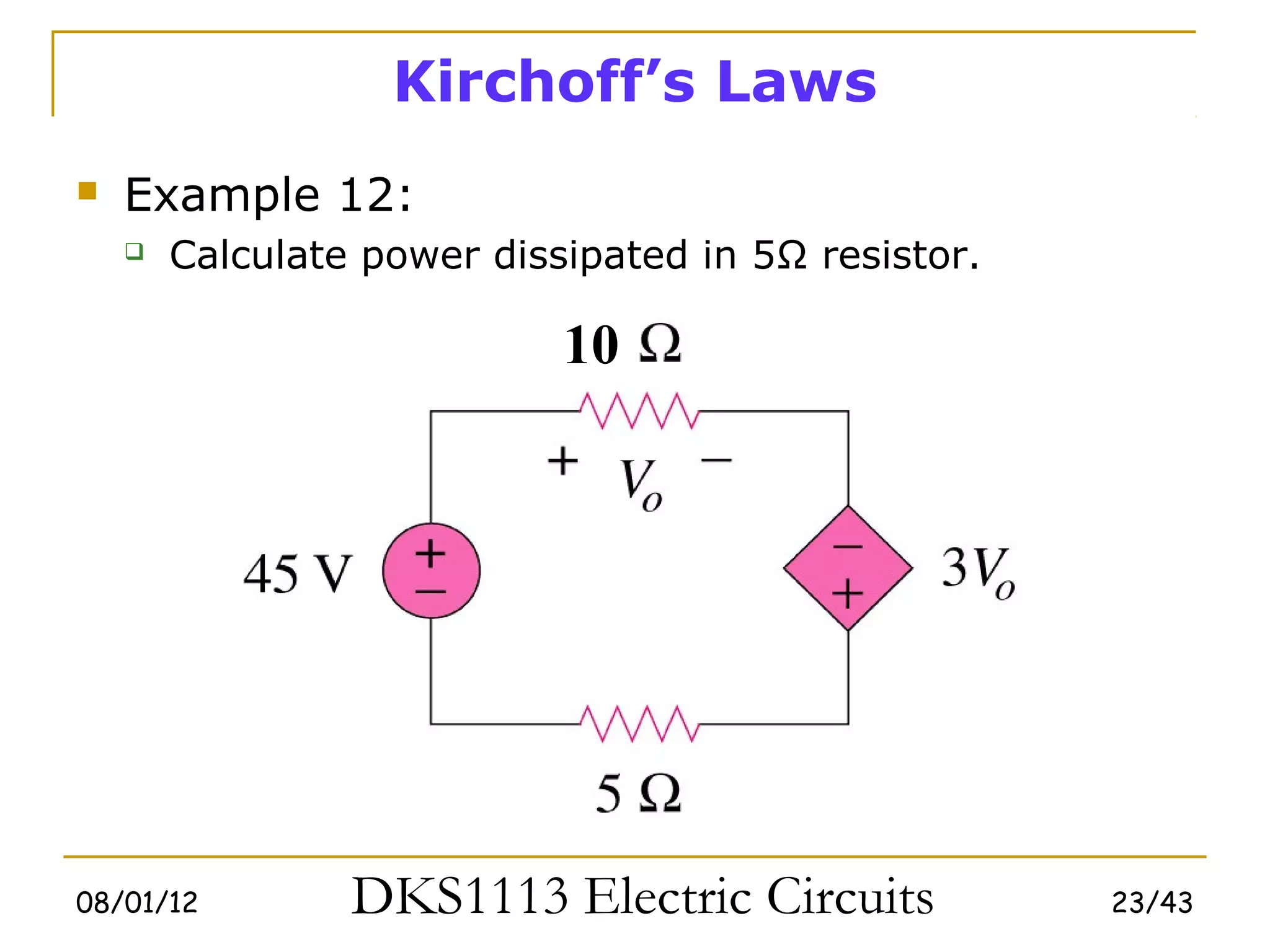
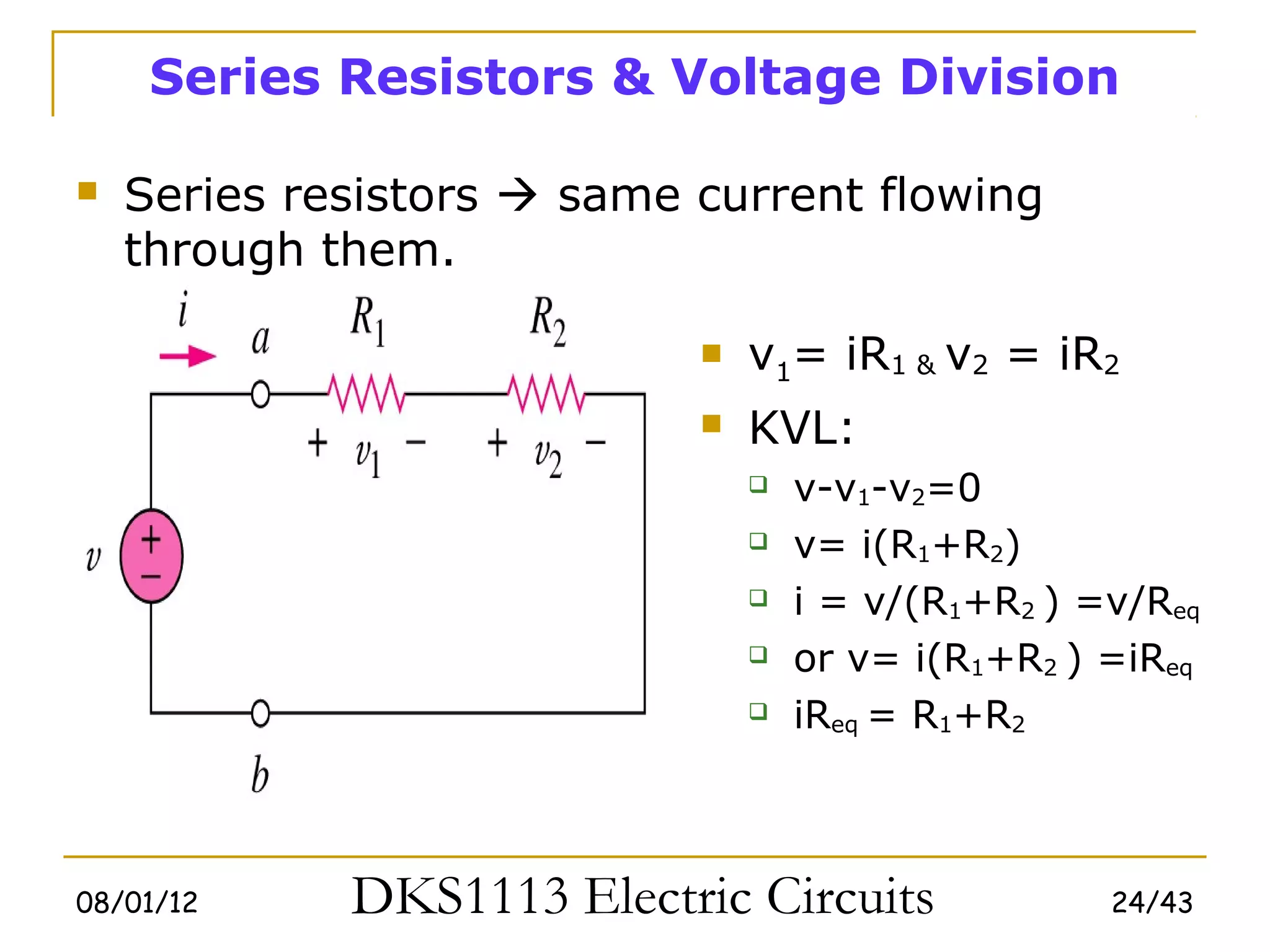
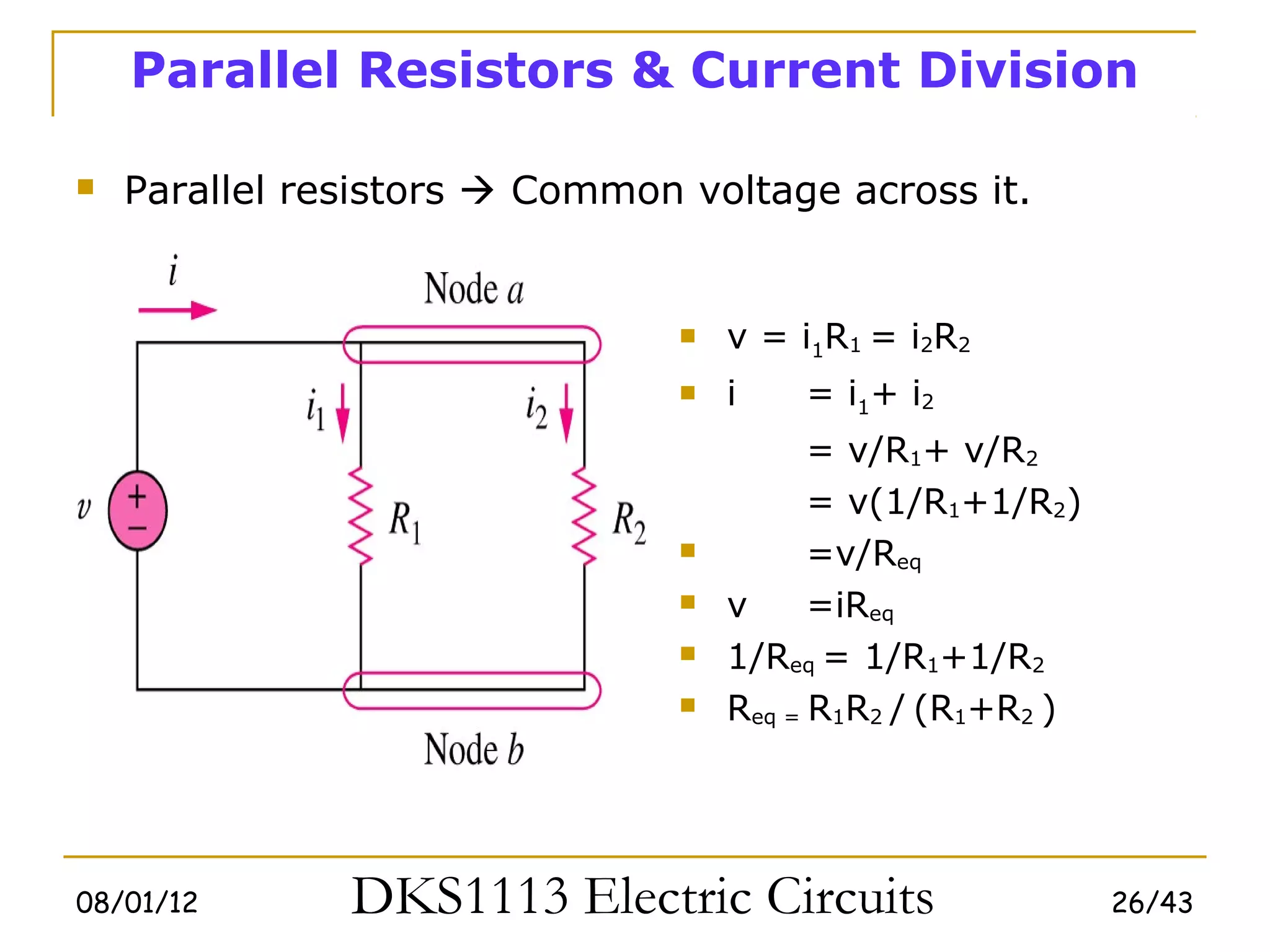
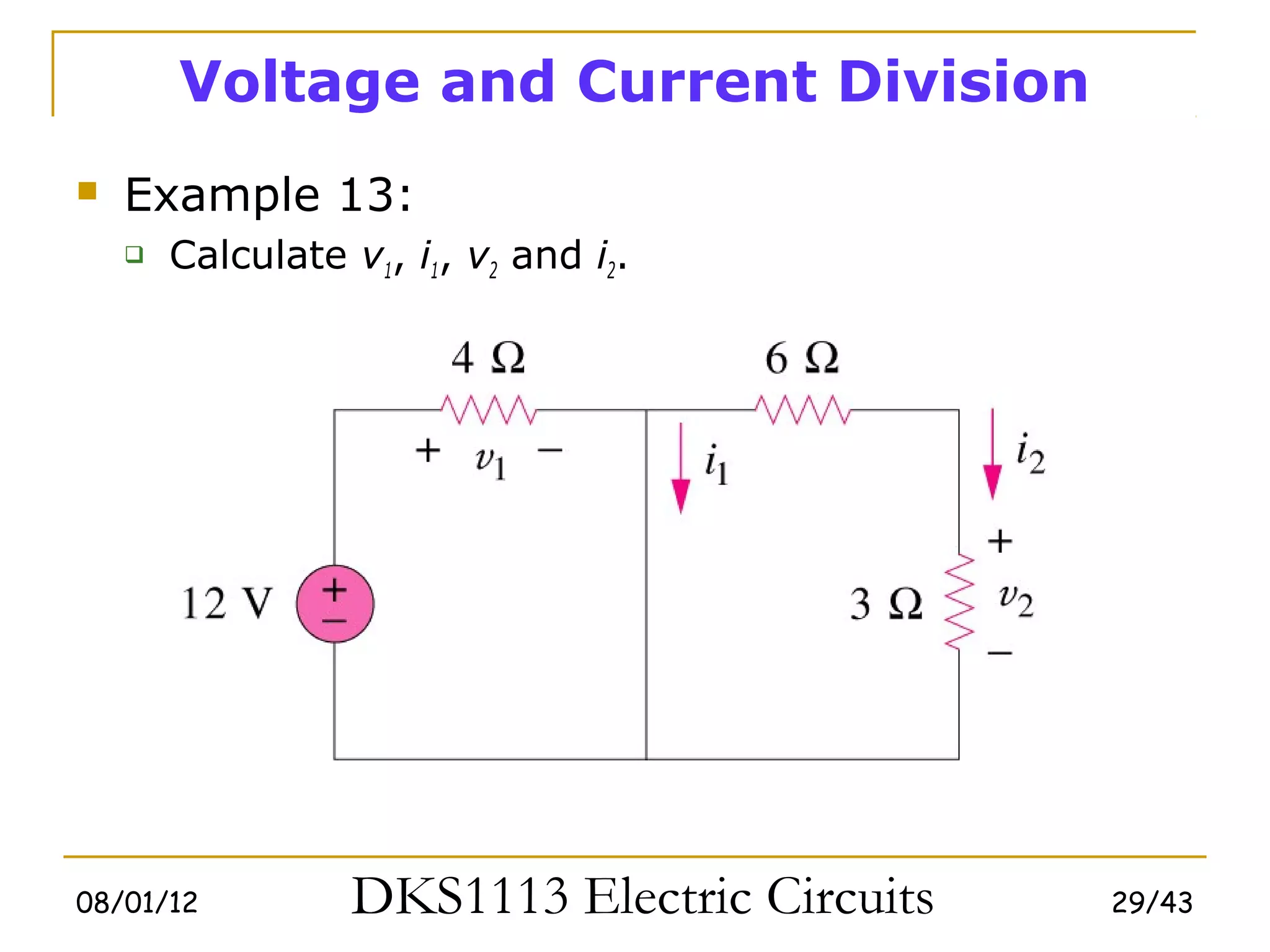
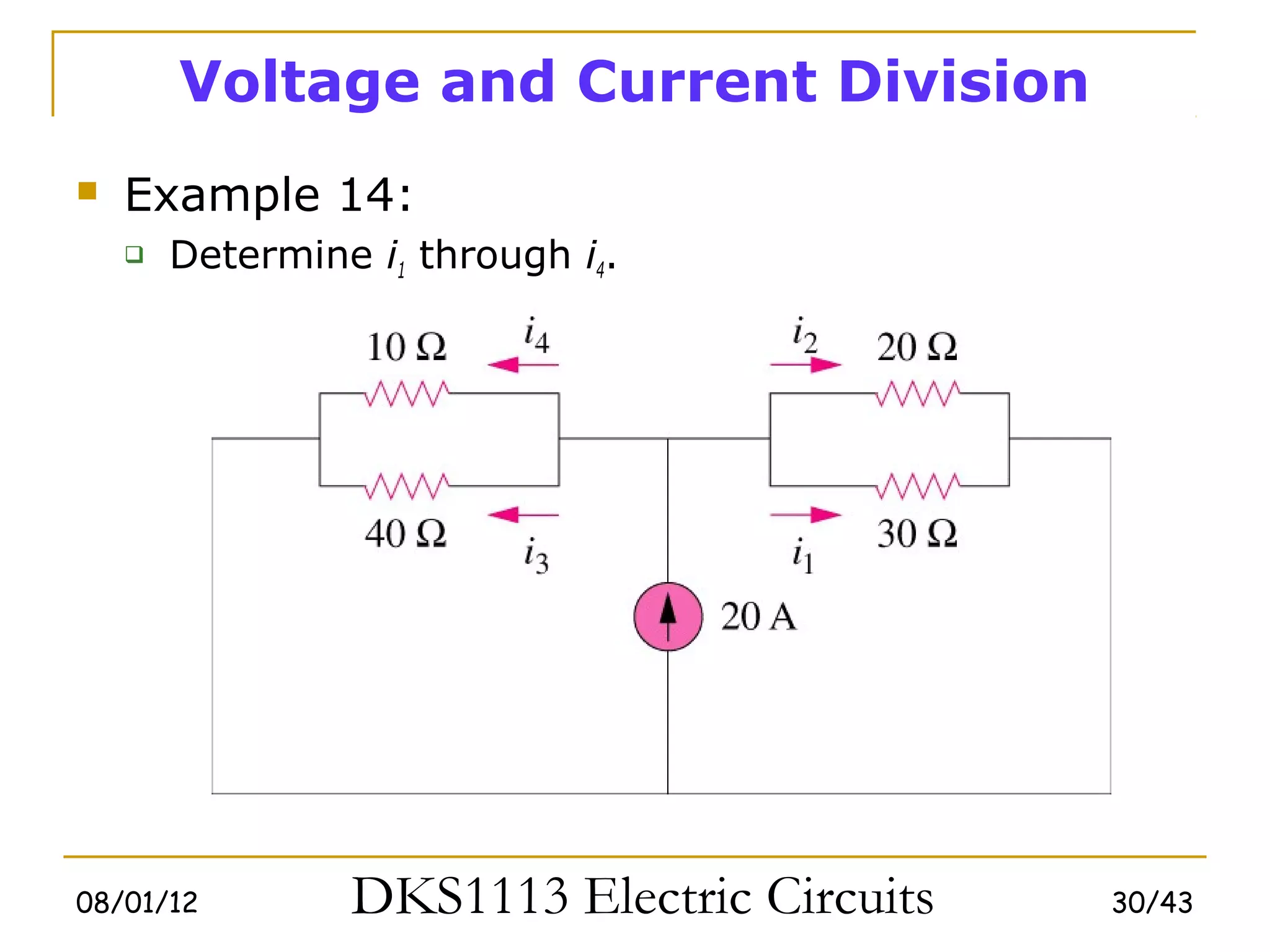
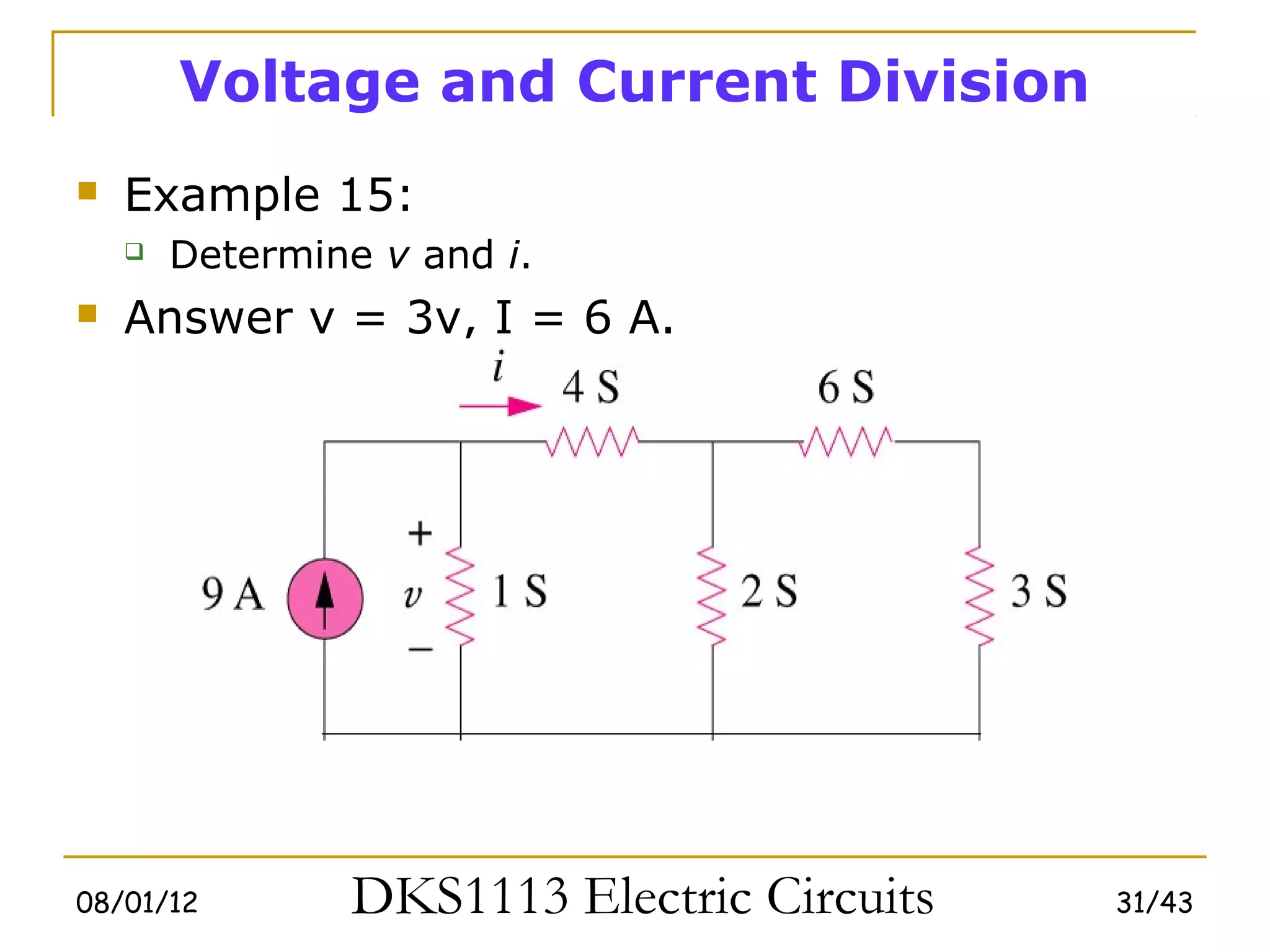
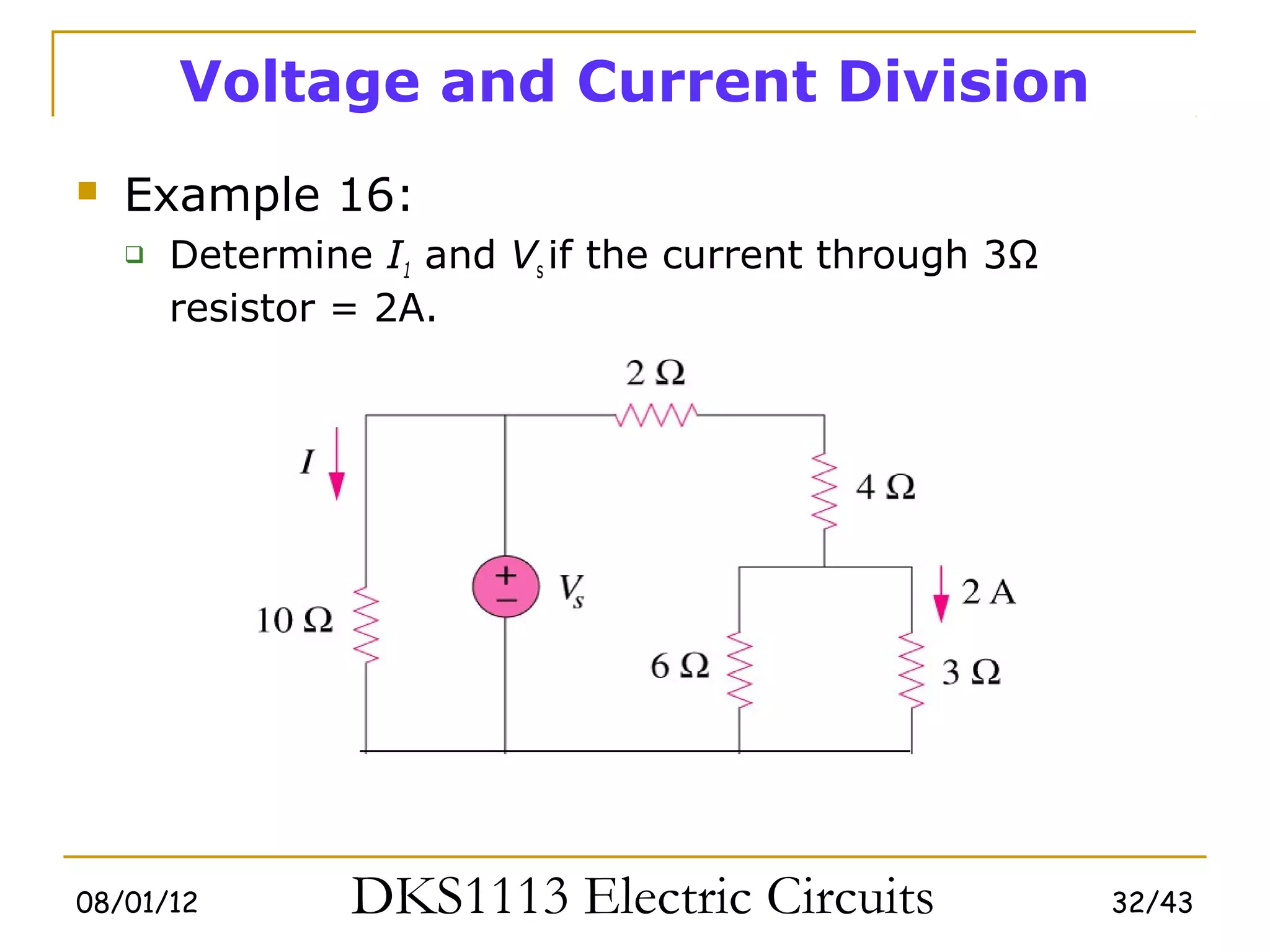
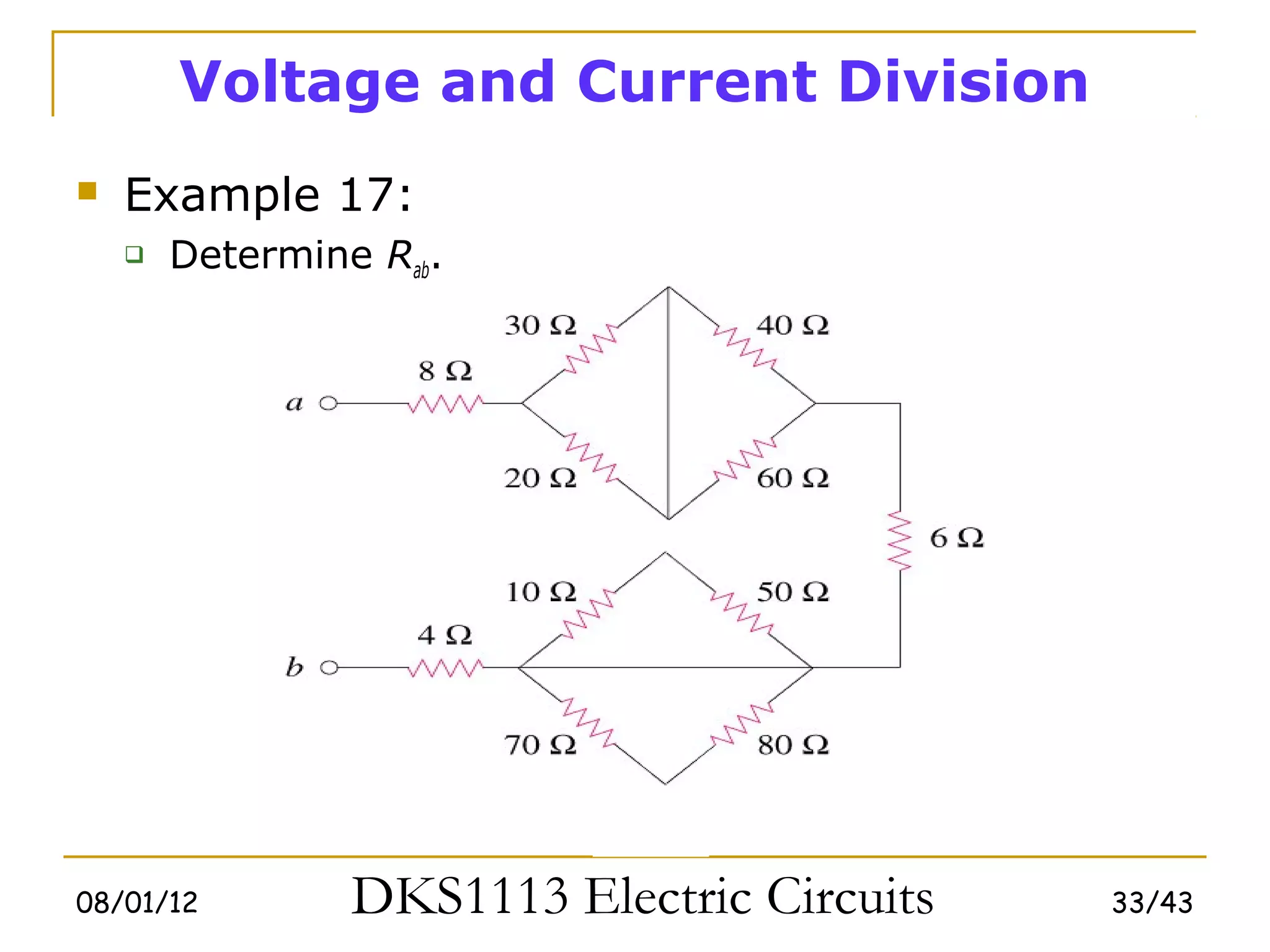
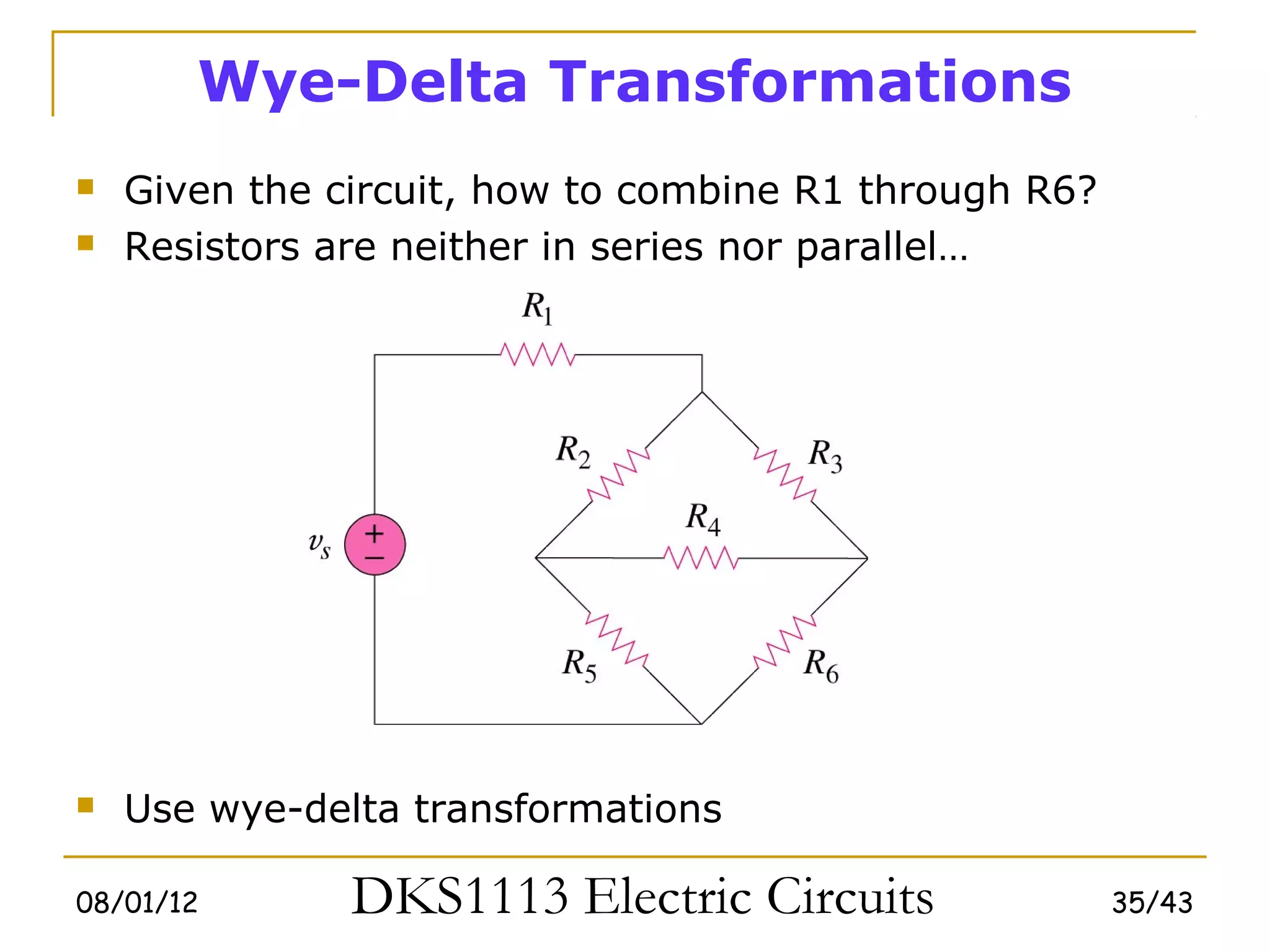
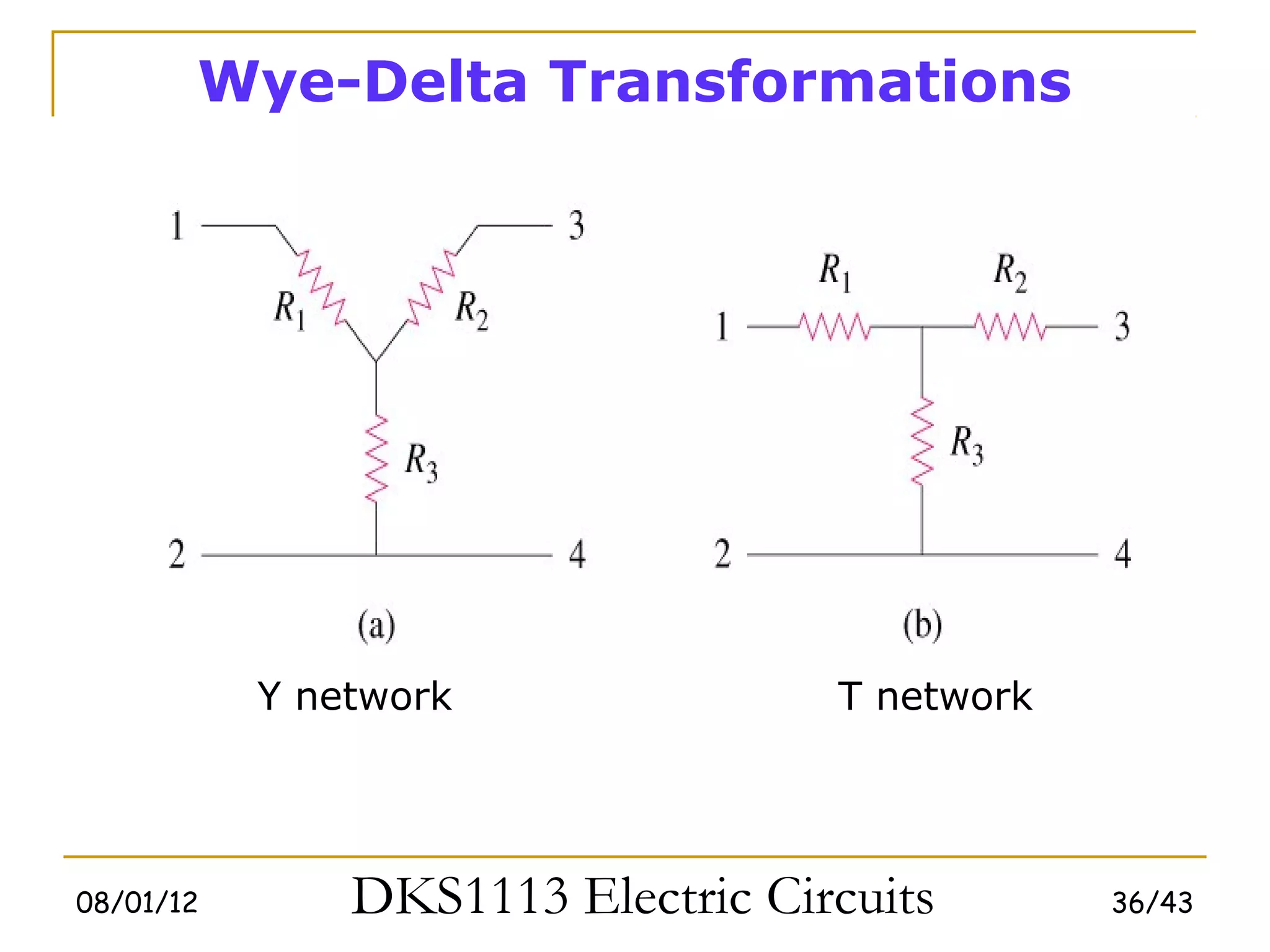
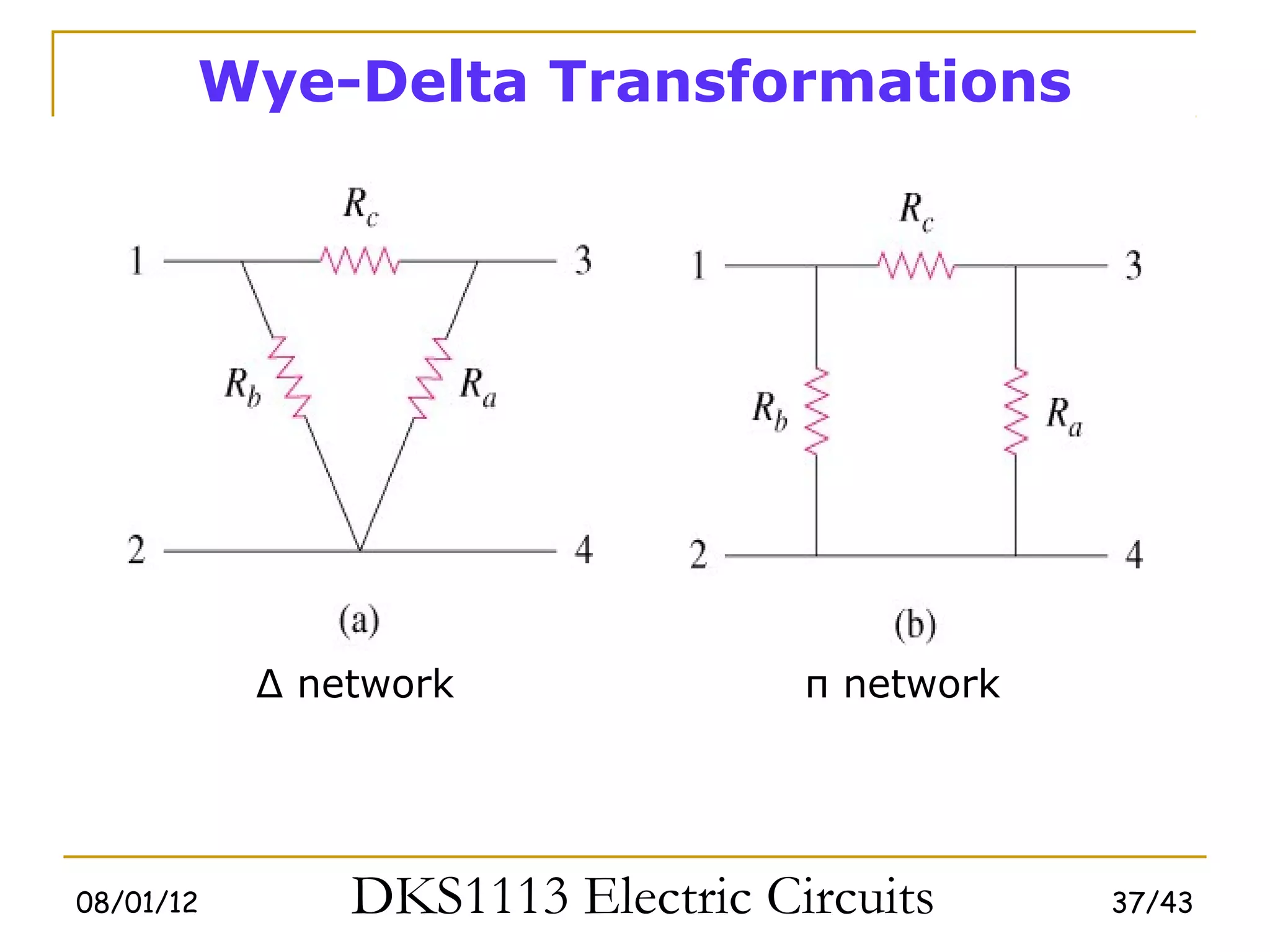
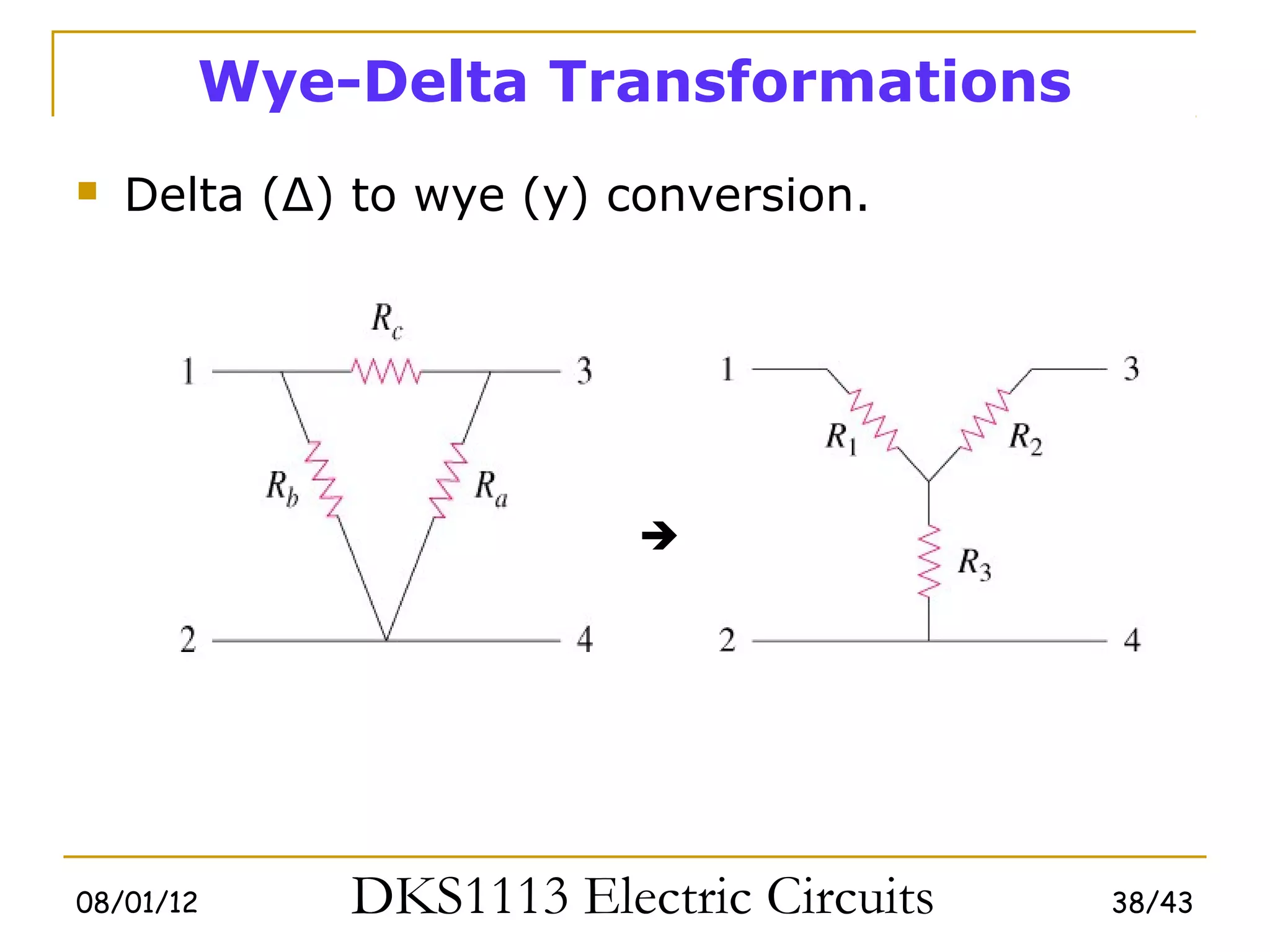
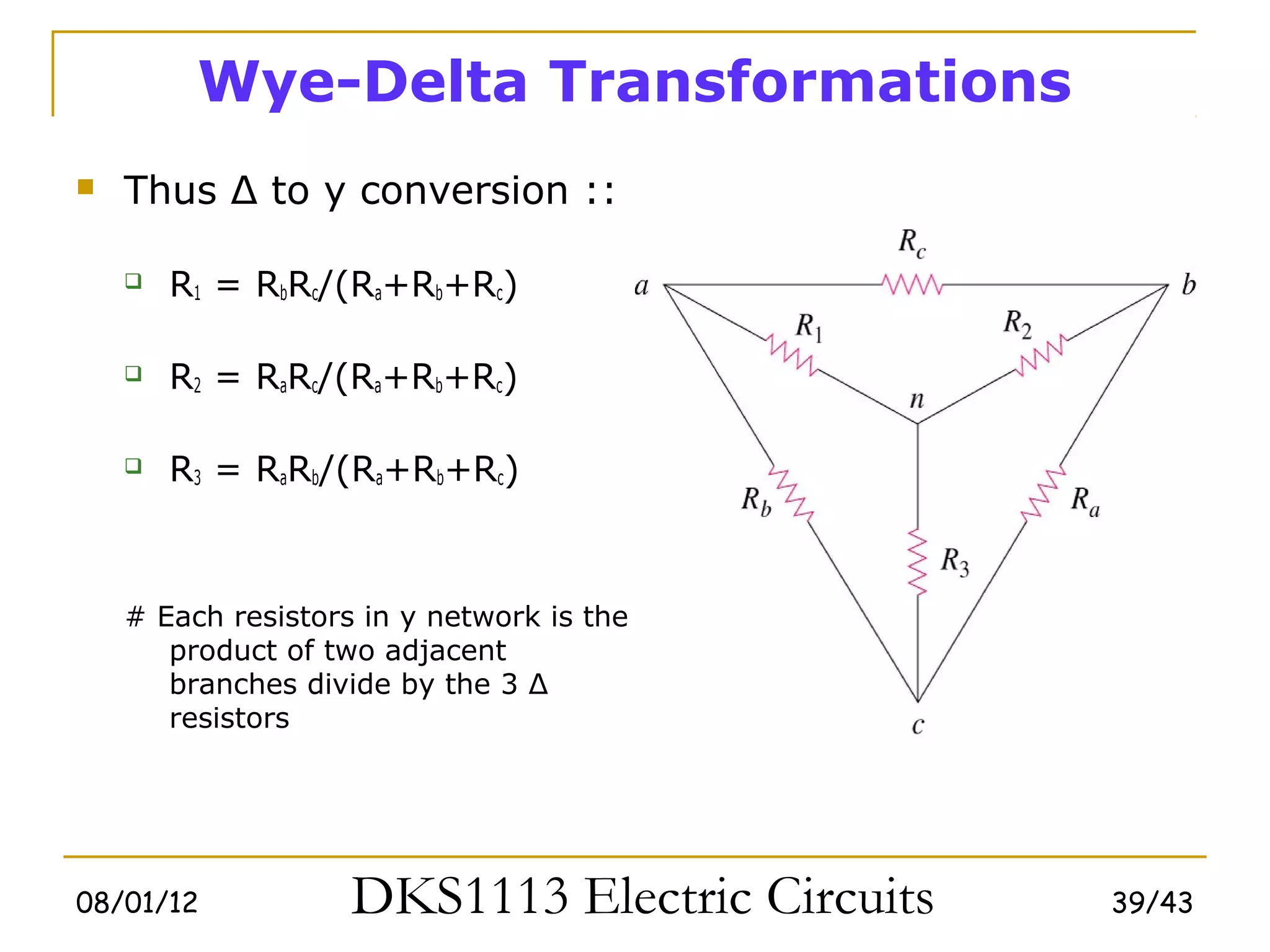
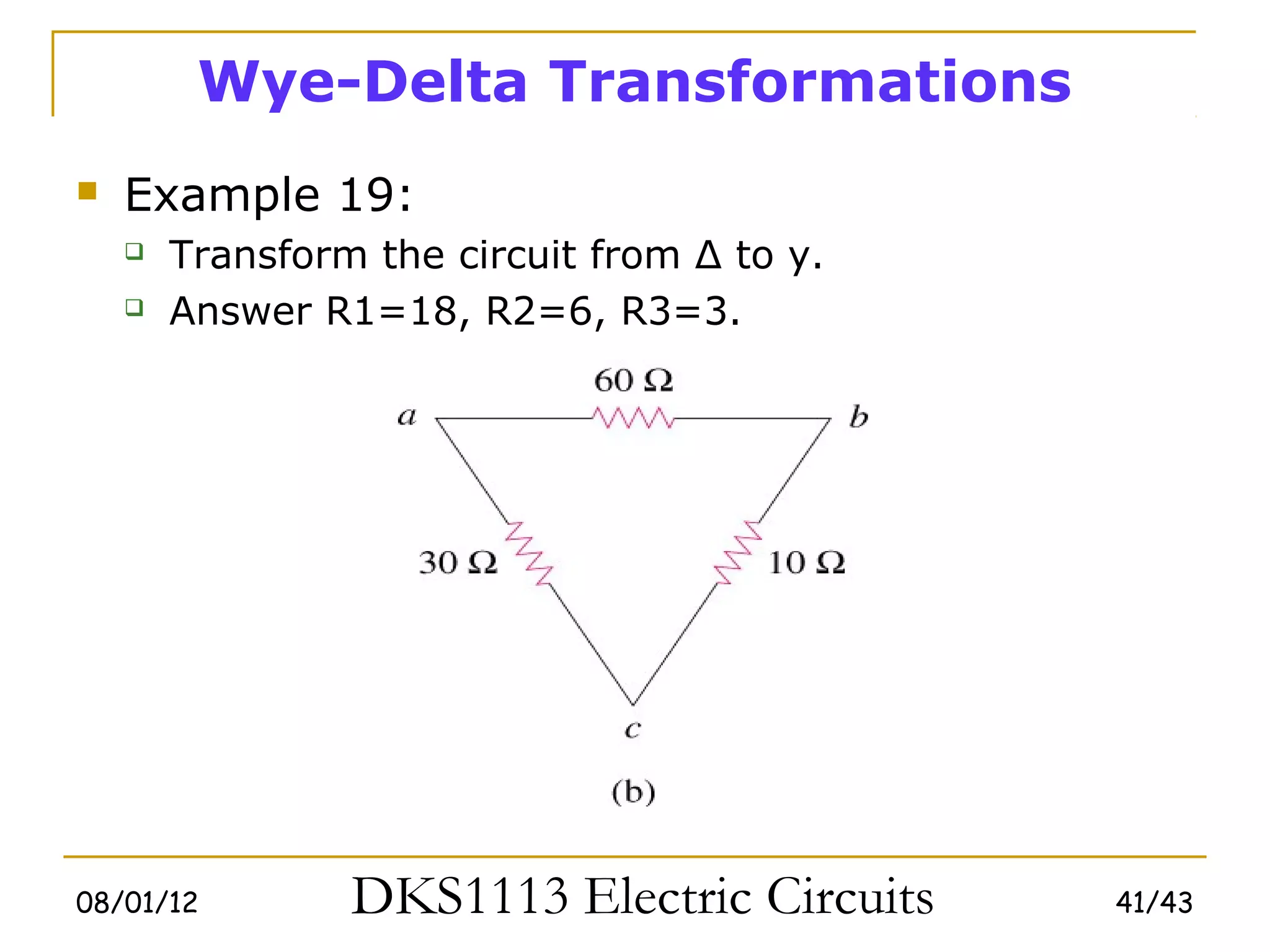
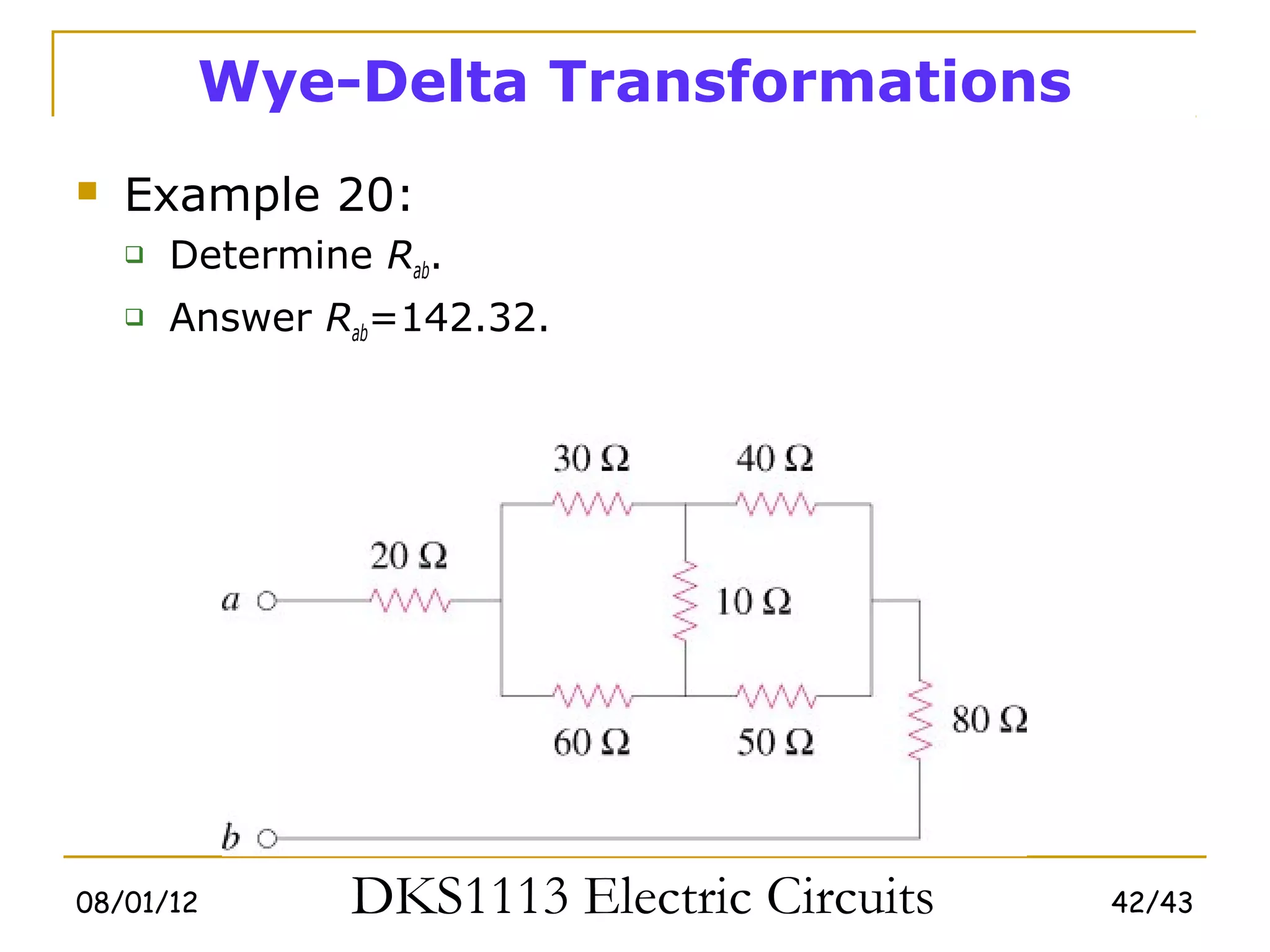
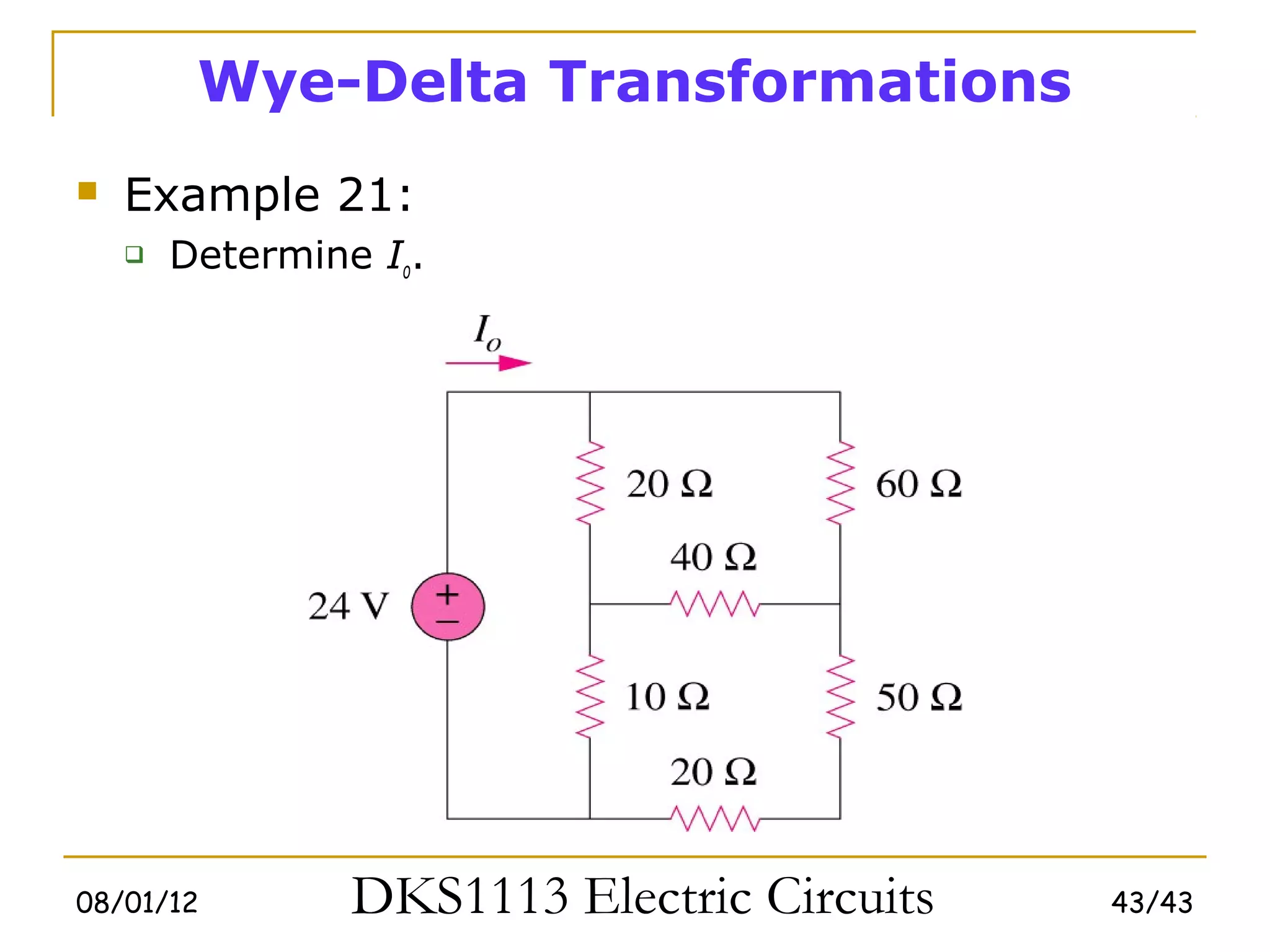
This document covers fundamental circuit analysis concepts including: 1) Ohm's law defines the relationship between current, voltage, and resistance in a circuit. Kirchoff's laws (KVL and KCL) are also introduced. 2) Series and parallel resistor combinations are examined along with voltage and current division techniques. 3) Wye-delta transformations allow the analysis of resistor networks that are neither purely series nor parallel.

1. 08/01/12
Chapter 2
Basic Laws
DKS1113 Electric Circuits

2. Introduction
 Fundament laws that govern electric circuits:
 Ohm’s Law.
 Kirchoff’s Law.
 These laws form the foundation upon which electric
circuit analysis is built.
 Common techniques in circuit analysis and design:
 Combining resistors in series and parallel.
 Voltage and current divisions.
 Wye to delta and delta to wye transformations.
 These techniques are restricted to resistive circuits.
08/01/12 DKS1113 Electric Circuits 2/43

3. Ohm’s Law
08/01/12 DKS1113 Electric Circuits 3/43

4. Ohm’s Law
 Relationship between current and voltage
within a circuit element.
 The voltage across an element is directly
proportional to the current flowing through it
v α i
 Thus::v=iR and R=v/i
 Where:
 R is called resistor.
 Has the ability to resist the flow of electric current.
 Measured in Ohms (Ω)
08/01/12 DKS1113 Electric Circuits 4/43

5. Ohm’s Law
*pay careful attention to current direction
v=iR
08/01/12 DKS1113 Electric Circuits 5/43

6. Ohm’s Law
 Value of R :: varies from 0 to infinity
 Extreme values == 0 & infinity.
 Only linear resistors obey Ohm’s Law.
Short circuit Open Circuit
08/01/12 DKS1113 Electric Circuits 6/43

7. Ohm’s Law
 Conductance (G)
 Unit mho or Siemens (S).
 Reciprocal of resistance R
G=1/R
 Has the ability to conduct electric current
08/01/12 DKS1113 Electric Circuits 7/43

8. Ohm’s Law
 Power:
 P = iv  i ( i R ) = i2R watts
 (v/R) v = v2/R watts
 R and G are positive quantities, thus power
is always positive.
 R absorbs power from the circuit  Passive
element.
08/01/12 DKS1113 Electric Circuits 8/43

9. Ohm’s Law
 Example 1:
 Determine voltage (v), conductance (G) and power
(p) from the figure below.
08/01/12 DKS1113 Electric Circuits 9/43

10. Ohm’s Law
 Example 2:
 Calculate current i in figure below when the switch
is in position 1.
 Find the current when the switch is in position 2.
08/01/12 DKS1113 Electric Circuits 10/43

11. Nodes, Branches & Loops
 Elements of electric circuits can be
interconnected in several way.
 Need to understand some basic concepts of
network topology.
 Branch: Represents a single element
(i.e. voltage, resistor & etc)
 Node: The meeting point between two
or more branches.
 Loop: Any closed path in a circuit.
08/01/12 DKS1113 Electric Circuits 11/43

12. Nodes, Branches & Loops
 Example 3:
 Determine how many branches and nodes for the
following circuit.
08/01/12 DKS1113 Electric Circuits 12/43

13. Nodes, Branches & Loops
 5 Branches  3 Nodes
 1 Voltage Source  a
 1 Current Source  b
 3 Resistors  c
08/01/12 DKS1113 Electric Circuits 13/43

14. Nodes, Branches & Loops
 Example 4:
 Determine how many branches and nodes for the
following circuit.
08/01/12 DKS1113 Electric Circuits 14/43

15. Kirchoff’s Laws
08/01/12 DKS1113 Electric Circuits 15/43

16. Kirchoff’s Laws
 Kirchoff’s Current Law (KCL)
 The algebraic sum of current entering /
leaving a node (or closed boundary) is zero.
 Current enters = +ve
 Current leaves = -ve
 ∑ current entering = ∑ current leaving
08/01/12 DKS1113 Electric Circuits 16/43

17. Kirchoff’s Laws
 Example 5:
 Given the following circuit, write the equation for
currents.
08/01/12 DKS1113 Electric Circuits 17/43

18. Kirchoff’s Laws
 Example 6:
 Current in a closed boundary
08/01/12 DKS1113 Electric Circuits 18/43

19. Kirchoff’s Laws
 Example 9:
 Use KCL to obtain currents i1, i2, and i3 in the circuit.
08/01/12 DKS1113 Electric Circuits 19/43

20. Kirchoff’s Laws
 Kirchoff’s Voltage Law (KVL)
 Applied to a loop in a circuit.
 According to KVL The algebraic sum of voltage (rises
and drops) in a loop is zero.
+ v1 - +
+
vs V2
-
- v3 + -
08/01/12 DKS1113 Electric Circuits 20/43

21. Kirchoff’s Laws
 Example 10:
 Use KVL to obtain v1, v2 and v3.
08/01/12 DKS1113 Electric Circuits 21/43

22. Kirchoff’s Laws
 Example 11:
 Use KVL to obtain v1, and v2.
08/01/12 DKS1113 Electric Circuits 22/43

23. Kirchoff’s Laws
 Example 12:
 Calculate power dissipated in 5Ω resistor.
10
08/01/12 DKS1113 Electric Circuits 23/43

24. Series Resistors & Voltage Division
 Series resistors  same current flowing
through them.
 v1= iR1 & v2 = iR2
 KVL:
 v-v1-v2=0
 v= i(R1+R2)
 i = v/(R1+R2 ) =v/Req
 or v= i(R1+R2 ) =iReq
 iReq = R1+R2
08/01/12 DKS1113 Electric Circuits 24/43

25. Series Resistors & Voltage Division
 Voltage Division:
 Previously:
 v1 = iR1 & v2 = iR2
 i = v/(R1+R2 )
 Thus:
 v1=vR1/(R1+R2)
 v2=vR2/(R1+R2)
08/01/12 DKS1113 Electric Circuits 25/43

26. Parallel Resistors & Current Division
 Parallel resistors  Common voltage across it.
 v = i1R1 = i2R2
 i = i1+ i2
= v/R1+ v/R2
= v(1/R1+1/R2)
 =v/Req
 v =iReq
 1/Req = 1/R1+1/R2
 Req = R1R2 / (R1+R2 )
08/01/12 DKS1113 Electric Circuits 26/43

27. Parallel Resistors & Current Division
 Current Division:
 Previously:
 v = i1R1 = i2R2
 v=iReq = iR1R2 / (R1+R2 )
 and i1 = v /R1 & i2 =v/ R2
 Thus:
 i1= iR2/(R1+R2)
 i2= iR1/(R1+R2 )
08/01/12 DKS1113 Electric Circuits 27/43

28. Conductance (G)
 Series conductance:
 1/Geq = 1/G1 +1/G2+…
 Parallel conductance:
 Geq = G1 +G2+…
08/01/12 DKS1113 Electric Circuits 28/43

29. Voltage and Current Division
 Example 13:
 Calculate v1, i1, v2 and i2.
08/01/12 DKS1113 Electric Circuits 29/43

30. Voltage and Current Division
 Example 14:
 Determine i1 through i4.
08/01/12 DKS1113 Electric Circuits 30/43

31. Voltage and Current Division
 Example 15:
 Determine v and i.
 Answer v = 3v, I = 6 A.
08/01/12 DKS1113 Electric Circuits 31/43

32. Voltage and Current Division
 Example 16:
 Determine I1 and Vs if the current through 3Ω
resistor = 2A.
08/01/12 DKS1113 Electric Circuits 32/43

33. Voltage and Current Division
 Example 17:
 Determine Rab.
08/01/12 DKS1113 Electric Circuits 33/43

34. Voltage and Current Division
 Example 18:
 Determine vx and power absorbed by the 12Ω
resistor.
 Answer v = 2v, p = 1.92w.
08/01/12 DKS1113 Electric Circuits 34/43

35. Wye-Delta Transformations
 Given the circuit, how to combine R1 through R6?
 Resistors are neither in series nor parallel…
 Use wye-delta transformations
08/01/12 DKS1113 Electric Circuits 35/43

36. Wye-Delta Transformations
Y network T network
08/01/12 DKS1113 Electric Circuits 36/43

37. Wye-Delta Transformations
Δ network π network
08/01/12 DKS1113 Electric Circuits 37/43

38. Wye-Delta Transformations
 Delta (Δ) to wye (y) conversion.

08/01/12 DKS1113 Electric Circuits 38/43

39. Wye-Delta Transformations
 Thus Δ to y conversion ::
 R1 = RbRc/(Ra+Rb+Rc)
 R2 = RaRc/(Ra+Rb+Rc)
 R3 = RaRb/(Ra+Rb+Rc)
# Each resistors in y network is the
product of two adjacent
branches divide by the 3 Δ
resistors
08/01/12 DKS1113 Electric Circuits 39/43

40. Wye-Delta Transformations
 Y to Δ conversions:
 Ra = (R1R2 +R2 R3 +R1R3)/R1
 Rb = (R1R2 +R2 R3 +R1R3)/R2
 Rc= (R1R2 +R2 R3 +R1R3)/R3
08/01/12 DKS1113 Electric Circuits 40/43

41. Wye-Delta Transformations
 Example 19:
 Transform the circuit from Δ to y.
 Answer R1=18, R2=6, R3=3.
08/01/12 DKS1113 Electric Circuits 41/43

42. Wye-Delta Transformations
 Example 20:
 Determine Rab.
 Answer Rab=142.32.
08/01/12 DKS1113 Electric Circuits 42/43

43. Wye-Delta Transformations
 Example 21:
 Determine Io.
08/01/12 DKS1113 Electric Circuits 43/43