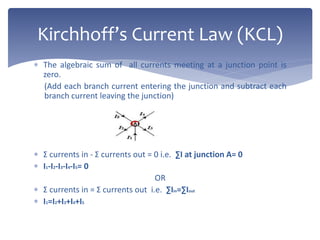
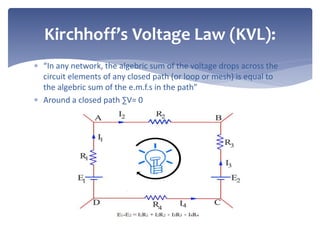
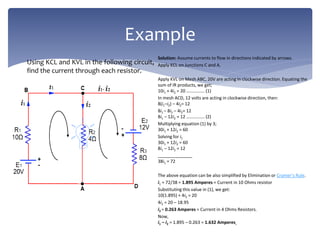
This document provides an overview of basic electrical engineering concepts including Ohm's Law, series and parallel circuits, and Kirchhoff's Laws. It defines Ohm's Law as stating that current is directly proportional to voltage and inversely proportional to resistance. Kirchhoff's Current Law and Voltage Law are introduced as the principles that the algebraic sum of currents at a junction is zero and the algebraic sum of voltages around a closed loop is also zero. An example circuit problem is worked through using these laws to solve for unknown currents.

1. Basic Electrical Engineering
ES103
Module I : DC Circuits and Network Theorems
Prepared By
Divya Asija,
Assistant Professor,
EEE Department,
ASET Noida

2.  Ohm’s Law: Ohm’s Law states that the current
flowing through a conductor is directly proportional
to the potential difference applied across its ends,
provided the temperature and other physical
conditions remain unchanged.
Or
 The current flowing through the electric circuit is
directly proportional to the potential difference
across the circuit and inversely proportional to the
resistance of the circuit, provided the temperature
remains constant.
Ohm’s law

3.  Potential difference ∝ Current i.e. V ∝ I
( When the value of V increases the value of I increases simultaneously)
V = IR
Where,
V is Voltage in volts (V)
R is Resistance in ohm (Ω)
I is Current in Ampere (A)
 Ohm’s Law Formula:
As an equation, the Ohm’s Law serves as an algebraic recipe for calculating the
current when the resistance and the potential difference are known. Likewise, if
any two parameters in the equation are known, then the unknown third
parameter can be easily calculated as follows:
To find : (i) Voltage(V)- V = IR,
(ii) Current(I)- I=V/R
(iii) Resistance (R)- R=V/I
Mathematical Equation of Ohm’s Law

4. 1. The electric current in a resistor wire is 4 A. When both ends are given a
potential of 12 Volts. What is the electrical resistance?
Solution: R=V/I
R= 12/4= 3 ohms
2. In an electric circuit, current of 1.5 microamps (1.5 μA) were to go through
a resistance of 2.3 mega-ohms (2.3 MΩ). How much voltage would be
“dropped” across this resistance?
Solution: V = IR
V= 1.5 ×10−6 A * 2.3 ×106 Ω= 3.45 V
Numerical Problems

5. Resistance in series and parallel
Series resistor properties: Parallel resistor properties

6. Resistance in series and parallel
Equivalent series resistance Equivalent parallel resistance
Rs= R1+R2+R3+…..Rn Rp= 1/R1+ 1/R2+….1/Rn

7. Voltage division in series circuit
V= IR1+IR2
Therefore, I= V/(R1+R2)
Total Voltage applied is equal to the sum of voltage drops V1 and V2 across R1
and R2.
V1= I. R1= V/(R1+R2). R1= [R1/(R1+R2)]V
Similarly V2= I. R2= V/(R1+R2). R2= [R2/(R1+R2)]V

8. Current division in parallel circuit
I= I1+I2 (1)
But V= I1R1= I2R2 (2)
Therefore I1= I2. (R2/R1) (3)
Putting (3) in (1) I= I2. [(R2/R1)+1]= I2. [(R2+R1)/R1] (4)
Thus I2= [R1/(R1+R2)]. I (5)
I1= I-I2 (substituting I2 value )
We get I1= [R2/(R1+R2)]. I (6)

9.  The algebraic sum of all currents meeting at a junction point is
zero.
(Add each branch current entering the junction and subtract each
branch current leaving the junction)
 Σ currents in - Σ currents out = 0 i.e. ∑I at junction A= 0
 I1-I2-I3-I4-I5= 0
OR
 Σ currents in = Σ currents out i.e. ∑Iin=∑Iout
 I1=I2+I3+I4+I5
Kirchhoff’s Current Law (KCL)

10.  “In any network, the algebric sum of the voltage drops across the
circuit elements of any closed path (or loop or mesh) is equal to
the algebric sum of the e.m.f.s in the path”
 Around a closed path ∑V= 0
Kirchhoff’s Voltage Law (KVL):

11. Example
Using KCL and KVL in the following circuit,
find the current through each resistor.
Solution: Assume currents to flow in directions indicated by arrows.
Apply KCL on Junctions C and A.
Apply KVL on Mesh ABC, 20V are acting in clockwise direction. Equating the
sum of IR products, we get;
10i1 + 4i2 = 20 ……………. (1)
In mesh ACD, 12 volts are acting in clockwise direction, then:
8(i1–i2) – 4i2= 12
8i1 – 8i2 – 4i2= 12
8i1 – 12i2 = 12 ……………. (2)
Multiplying equation (1) by 3;
30i1 + 12i2 = 60
Solving for i1
30i1 + 12i2 = 60
8i1 – 12i2 = 12
______________
38i1 = 72
The above equation can be also simplified by Elimination or Cramer’s Rule.
i1 = 72/38 = 1.895 Amperes = Current in 10 Ohms resistor
Substituting this value in (1), we get:
10(1.895) + 4i2 = 20
4i2 = 20 – 18.95
i2 = 0.263 Amperes = Current in 4 Ohms Resistors.
Now,
i1 – i2 = 1.895 – 0.263 = 1.632 Amperes