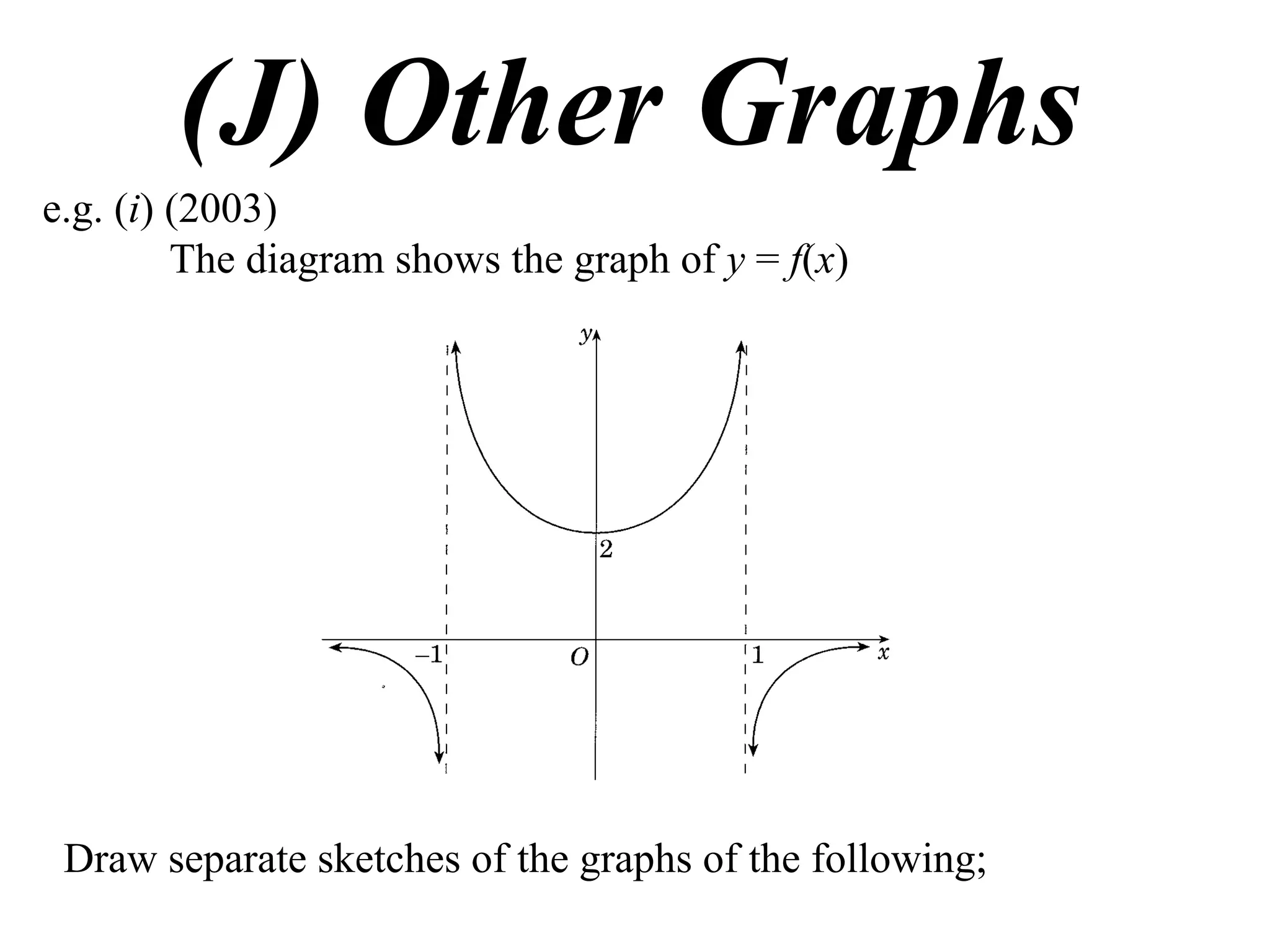
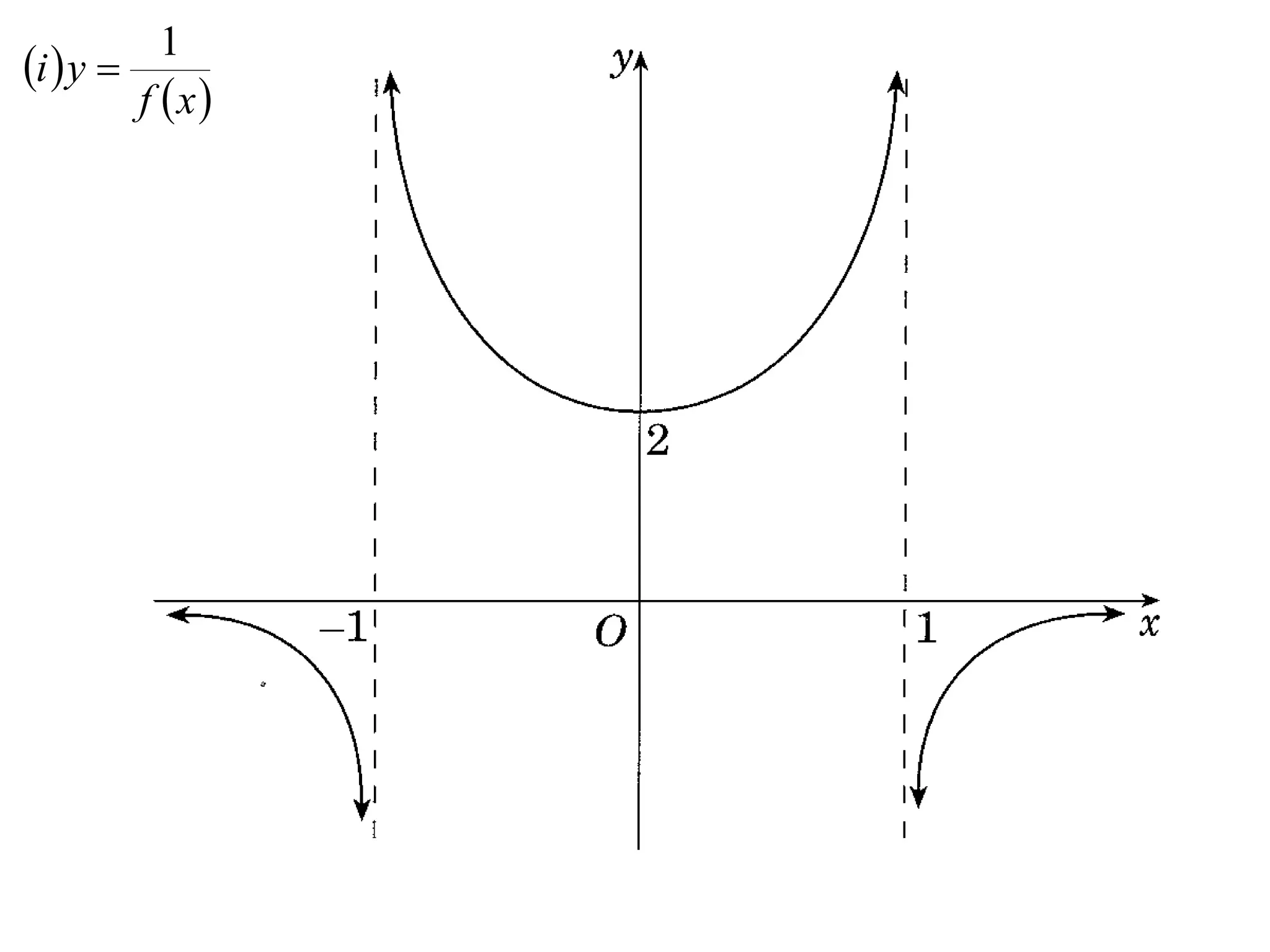
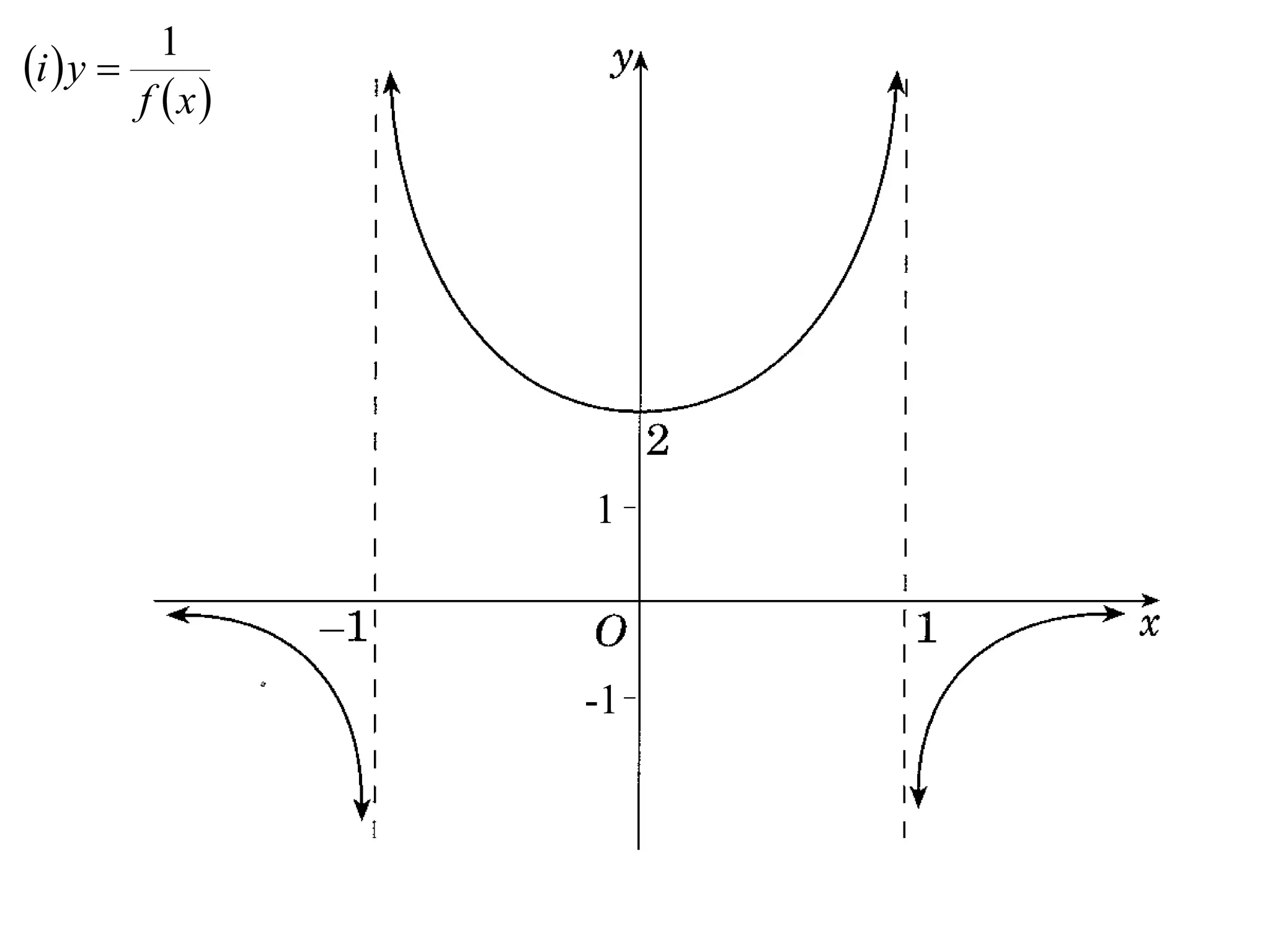
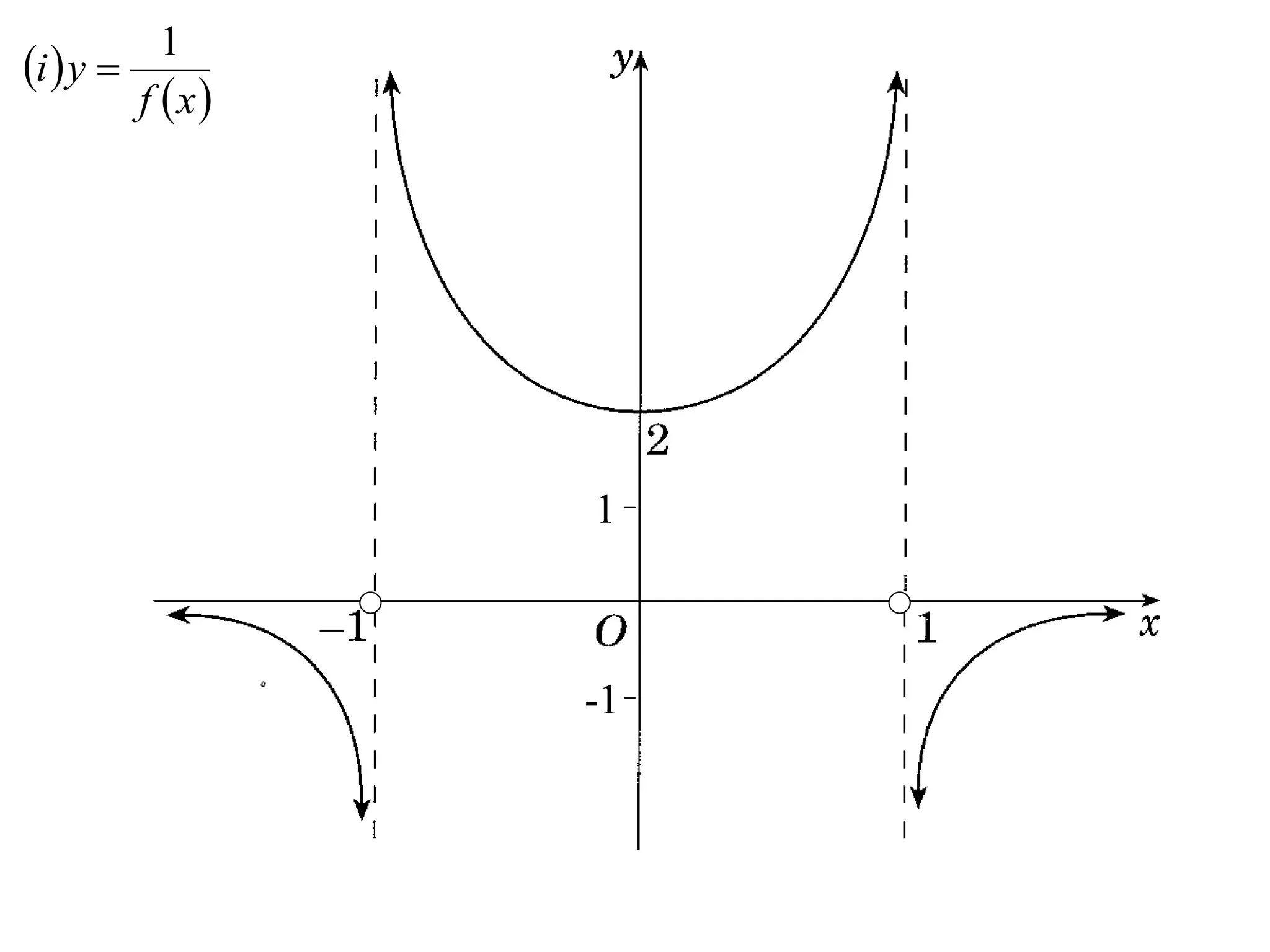
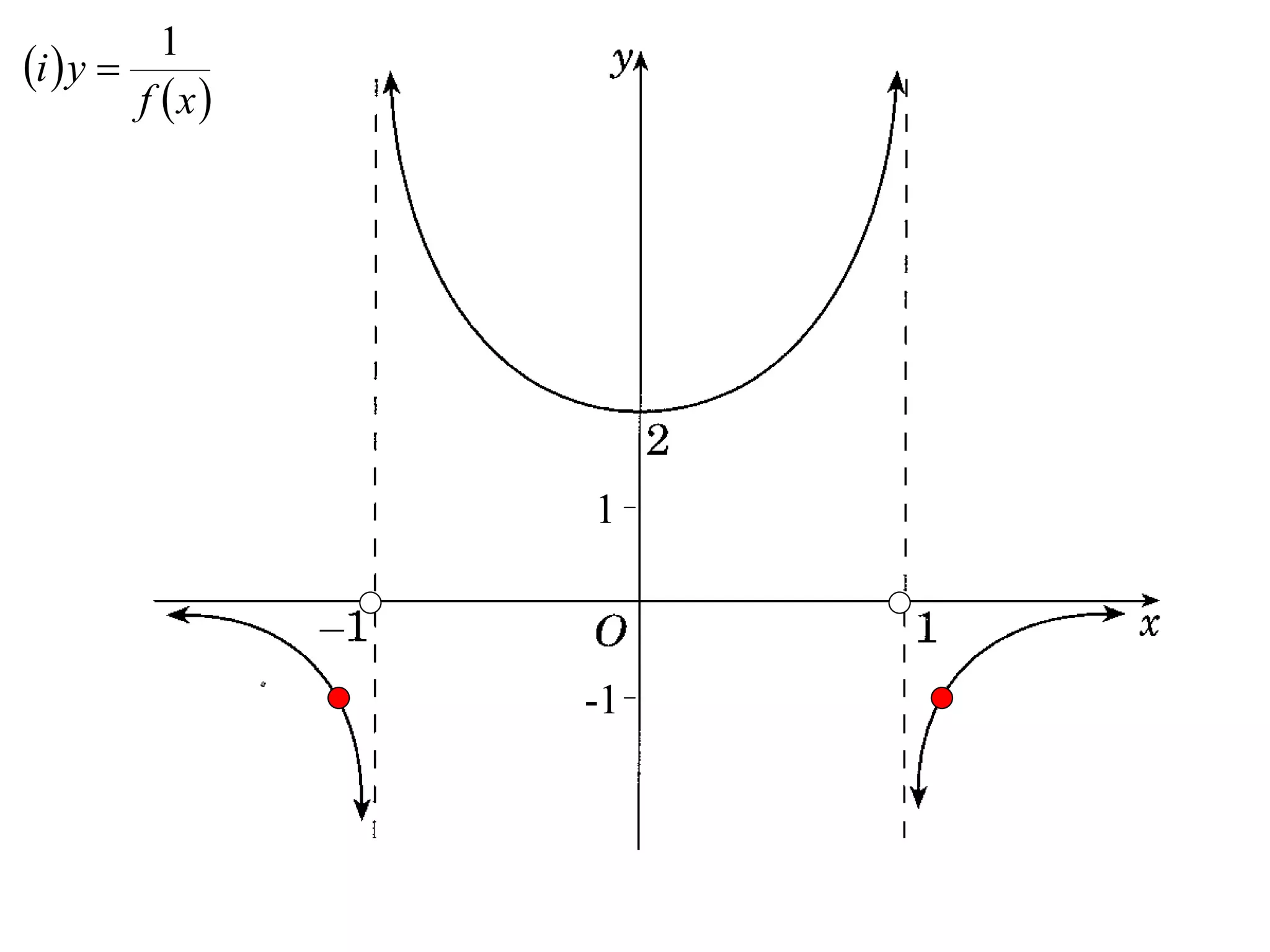
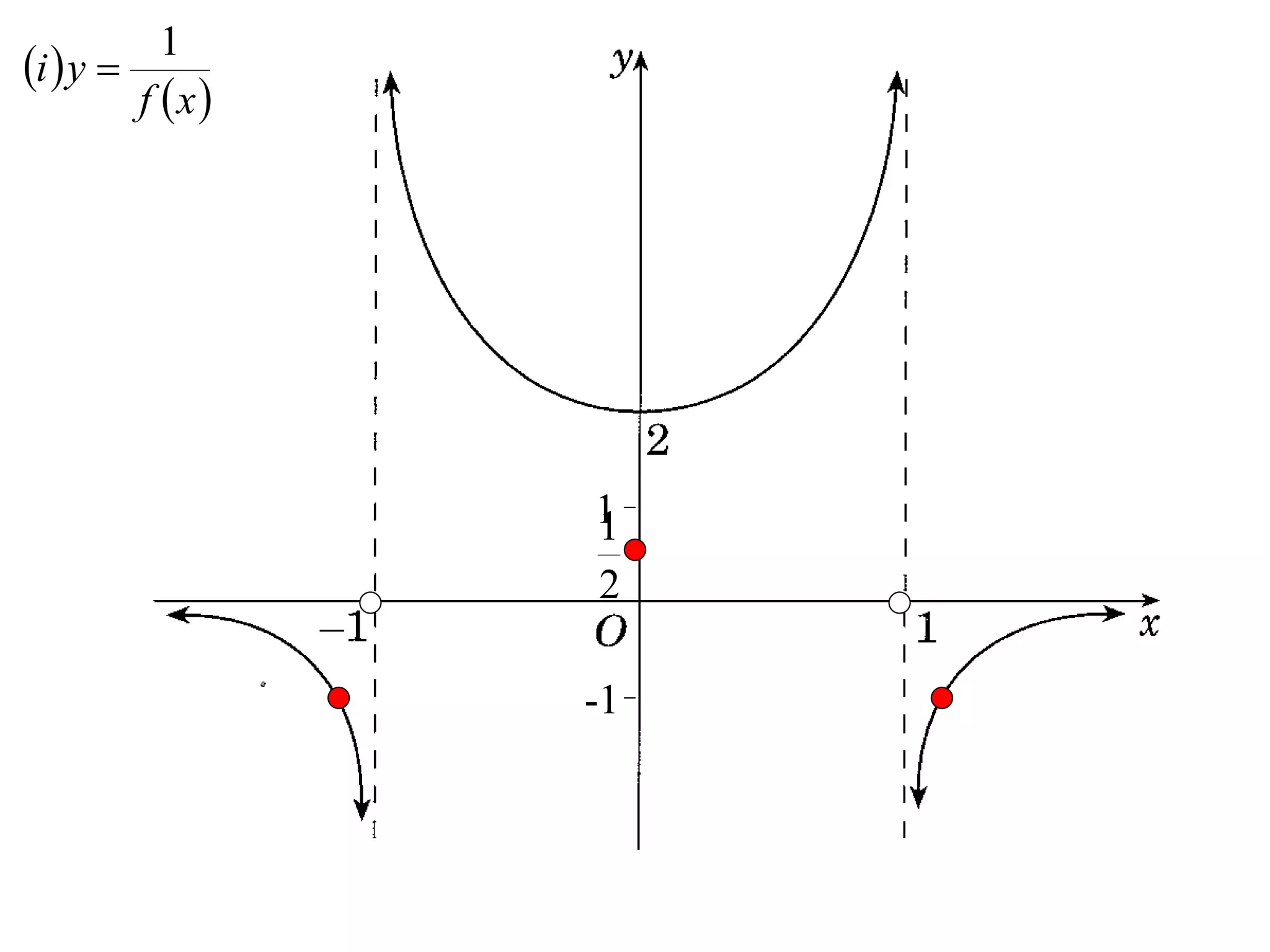
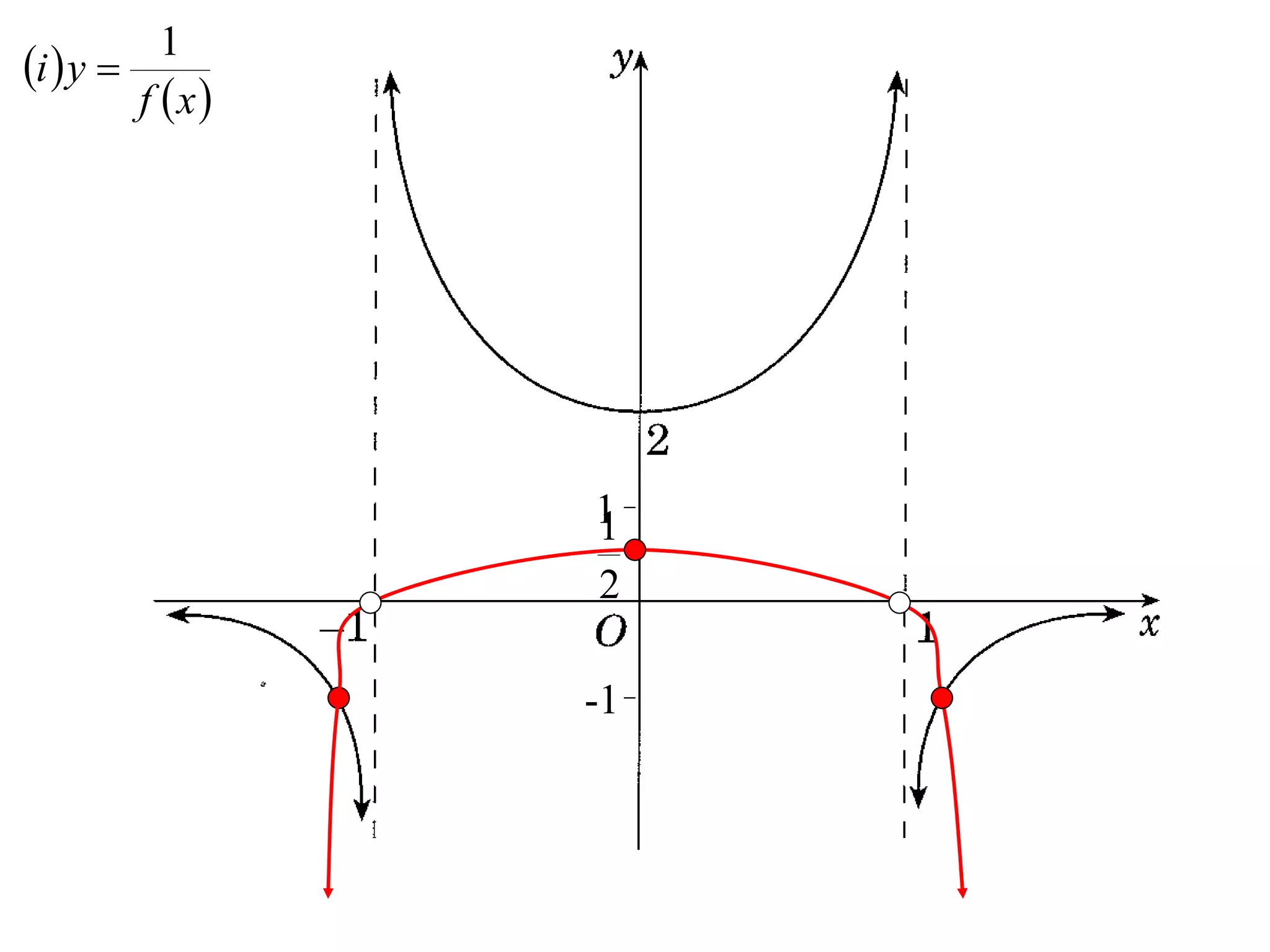
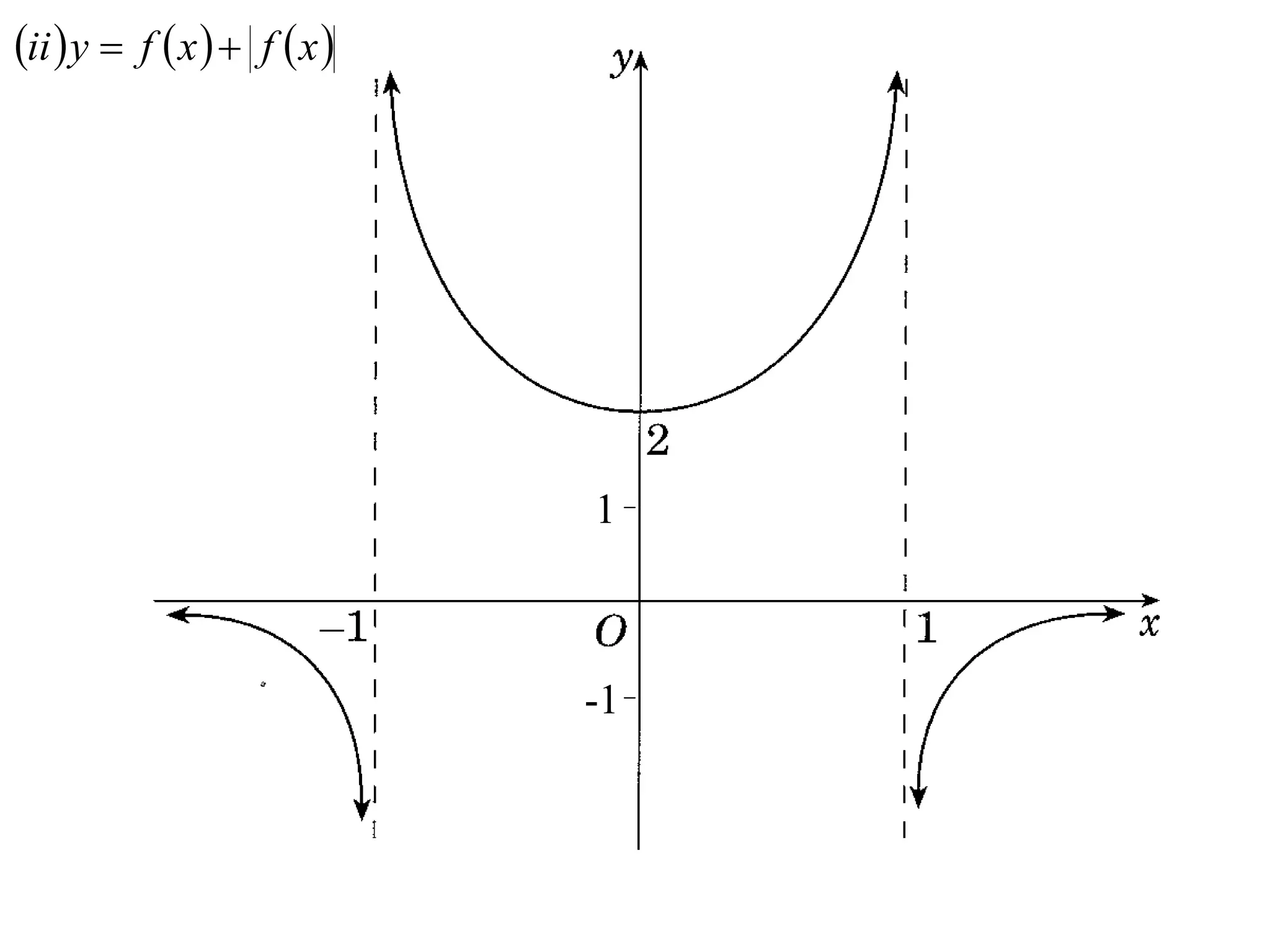
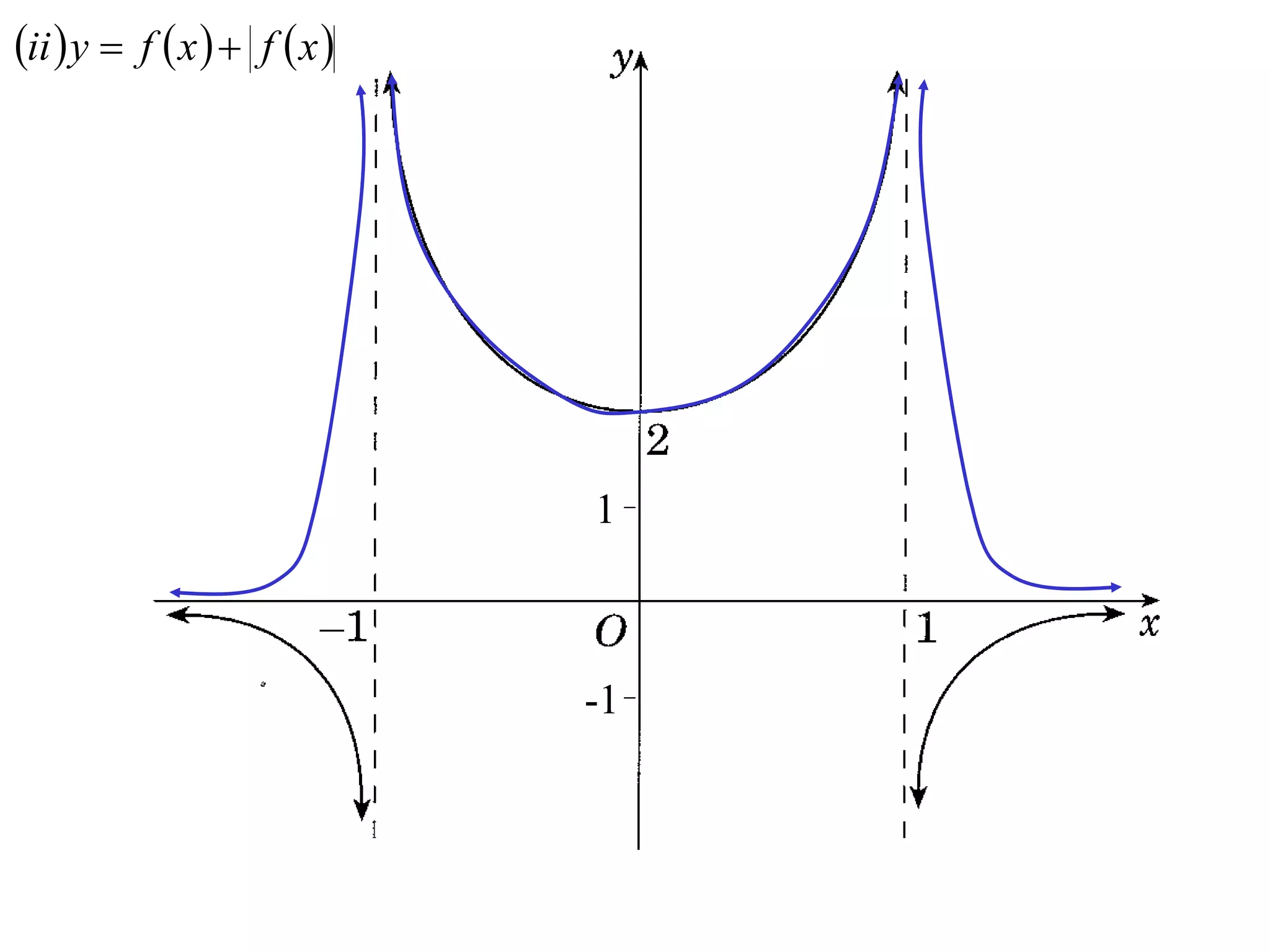
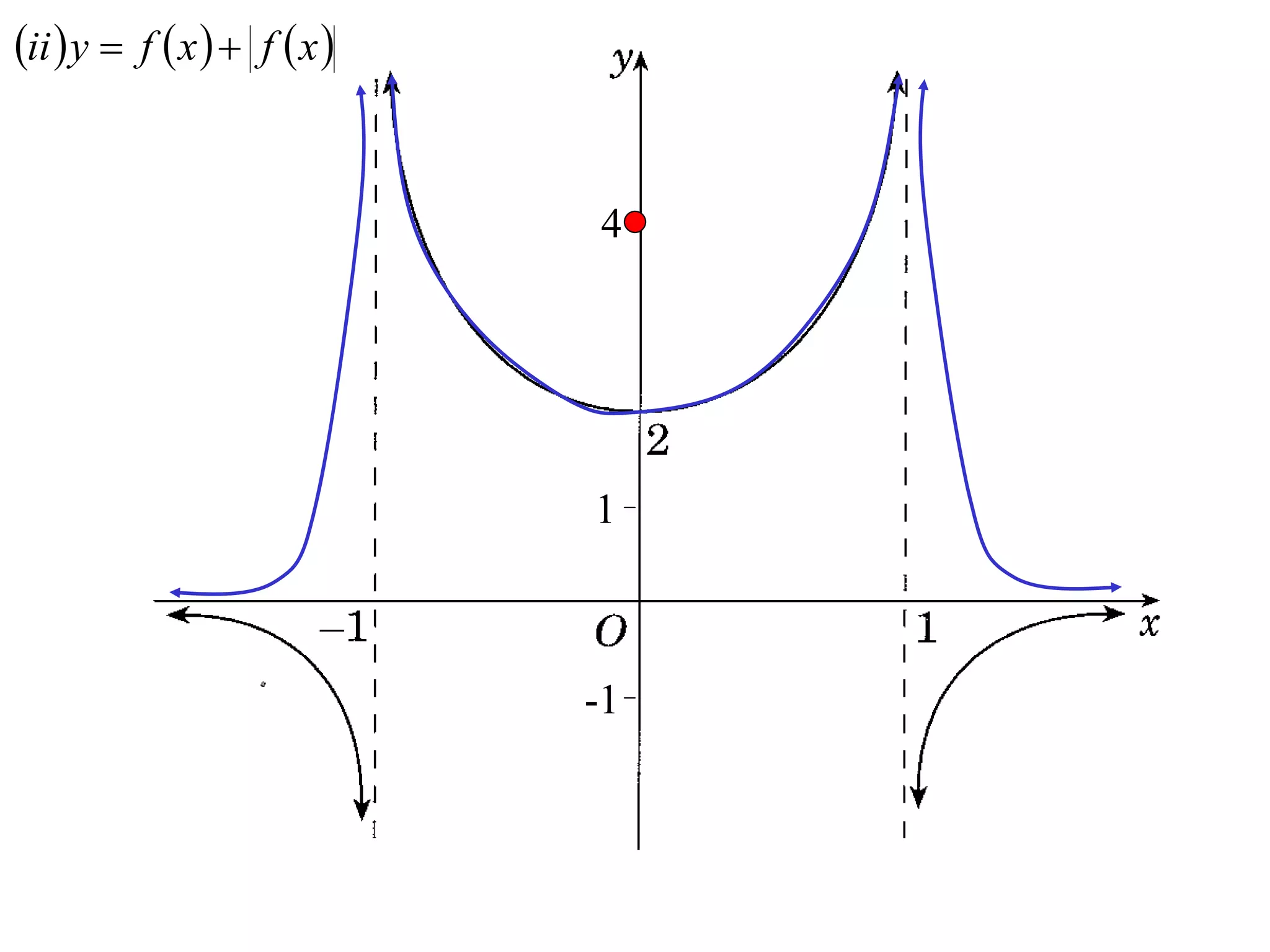
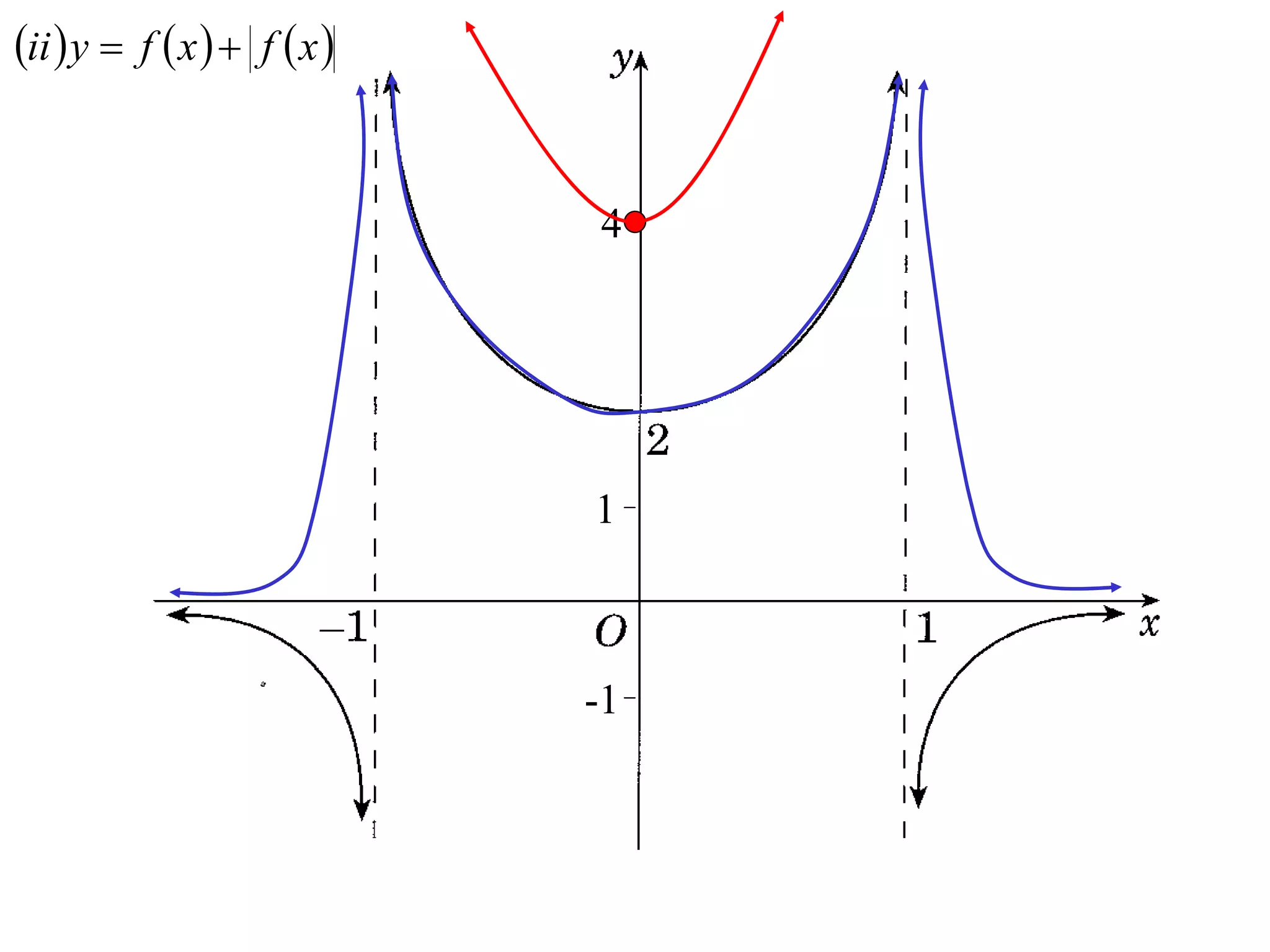
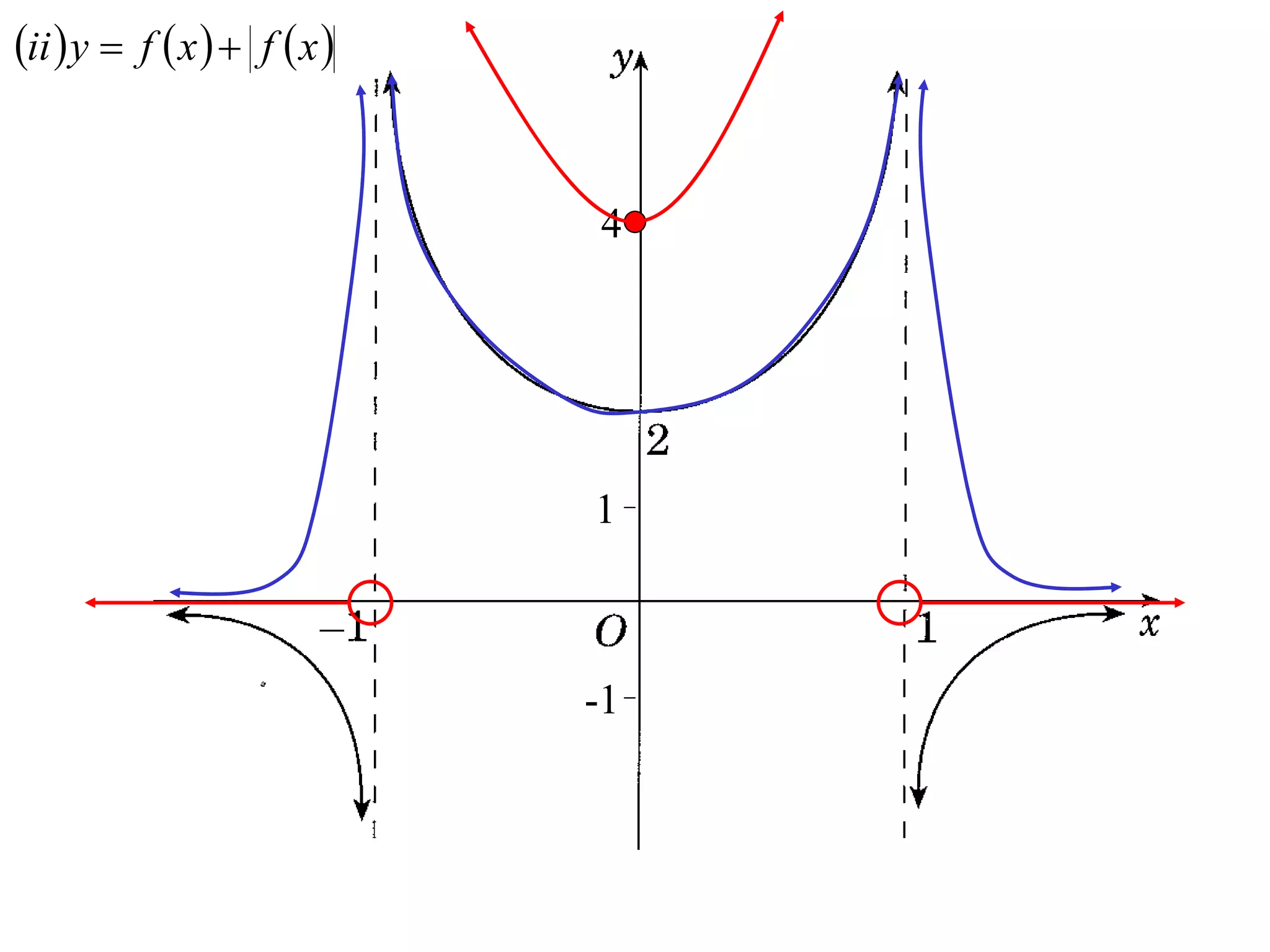
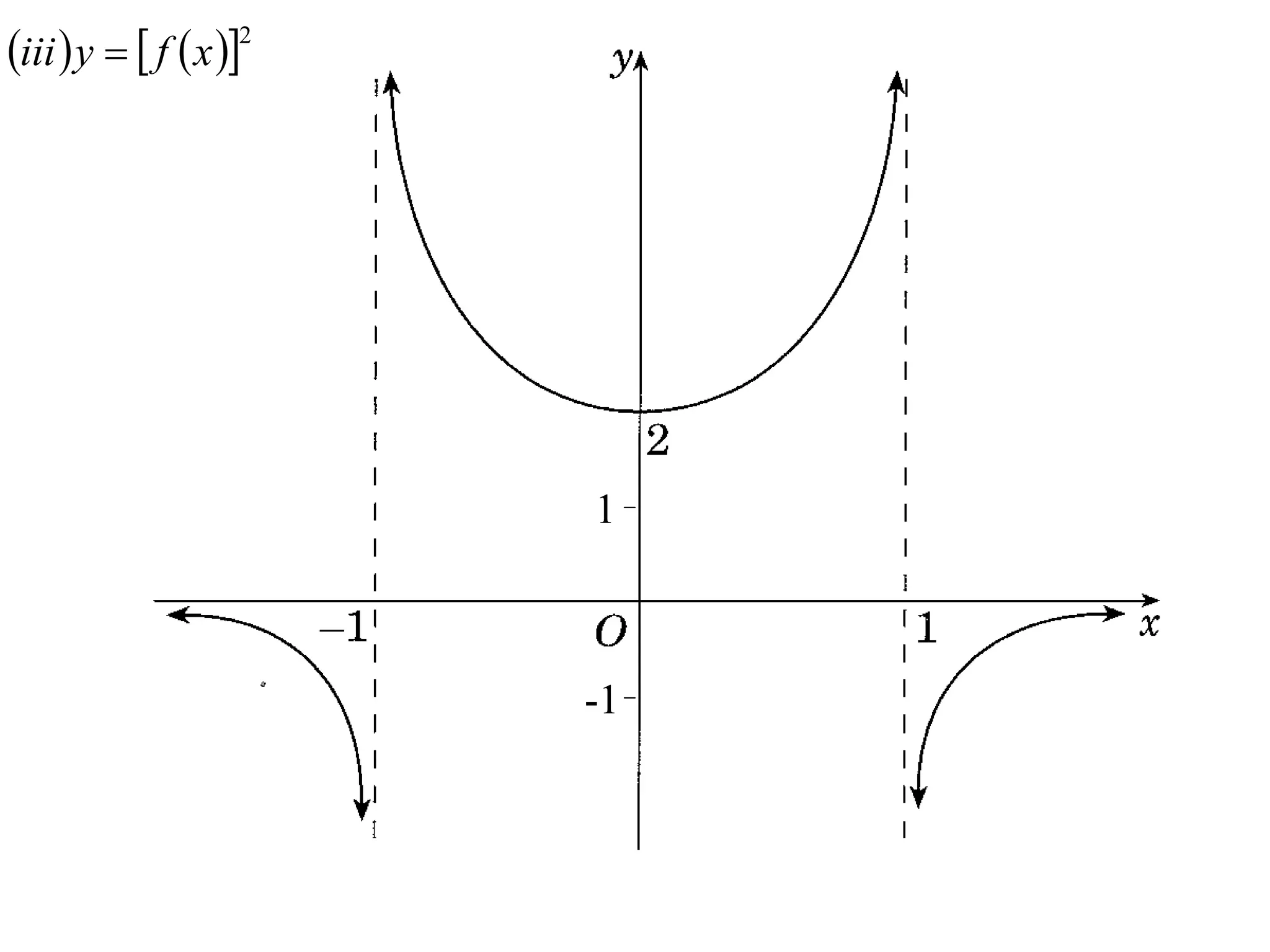
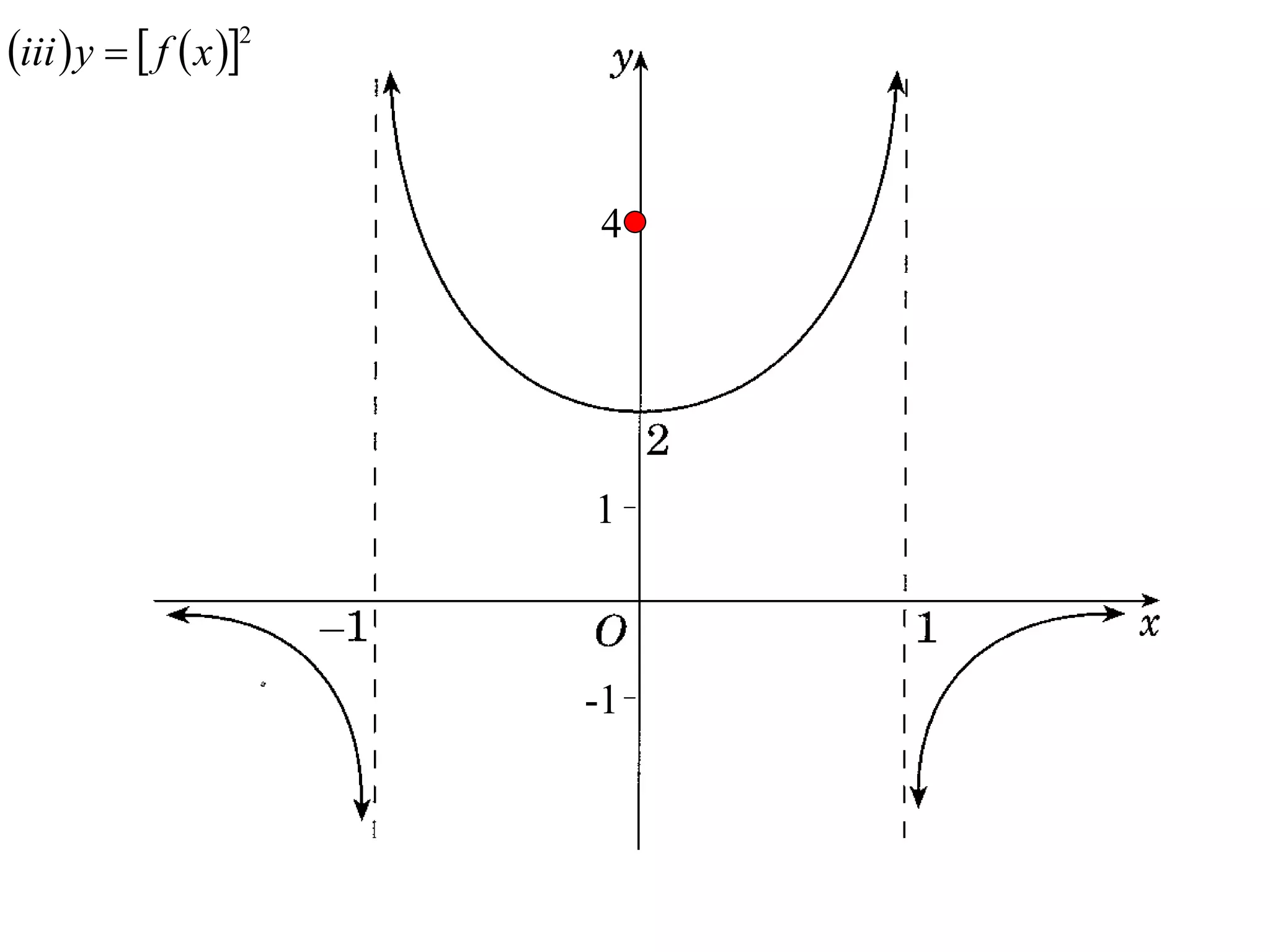
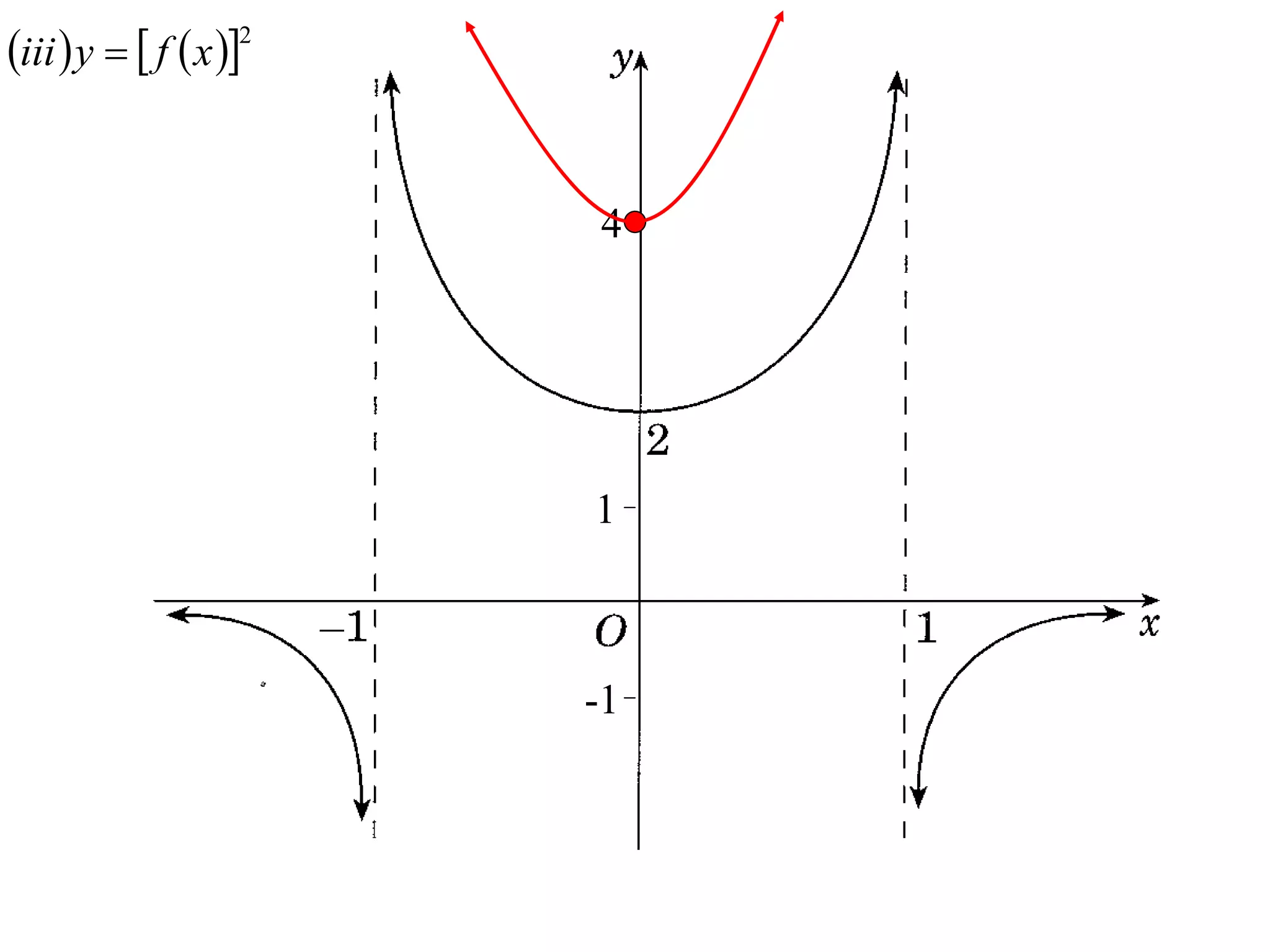
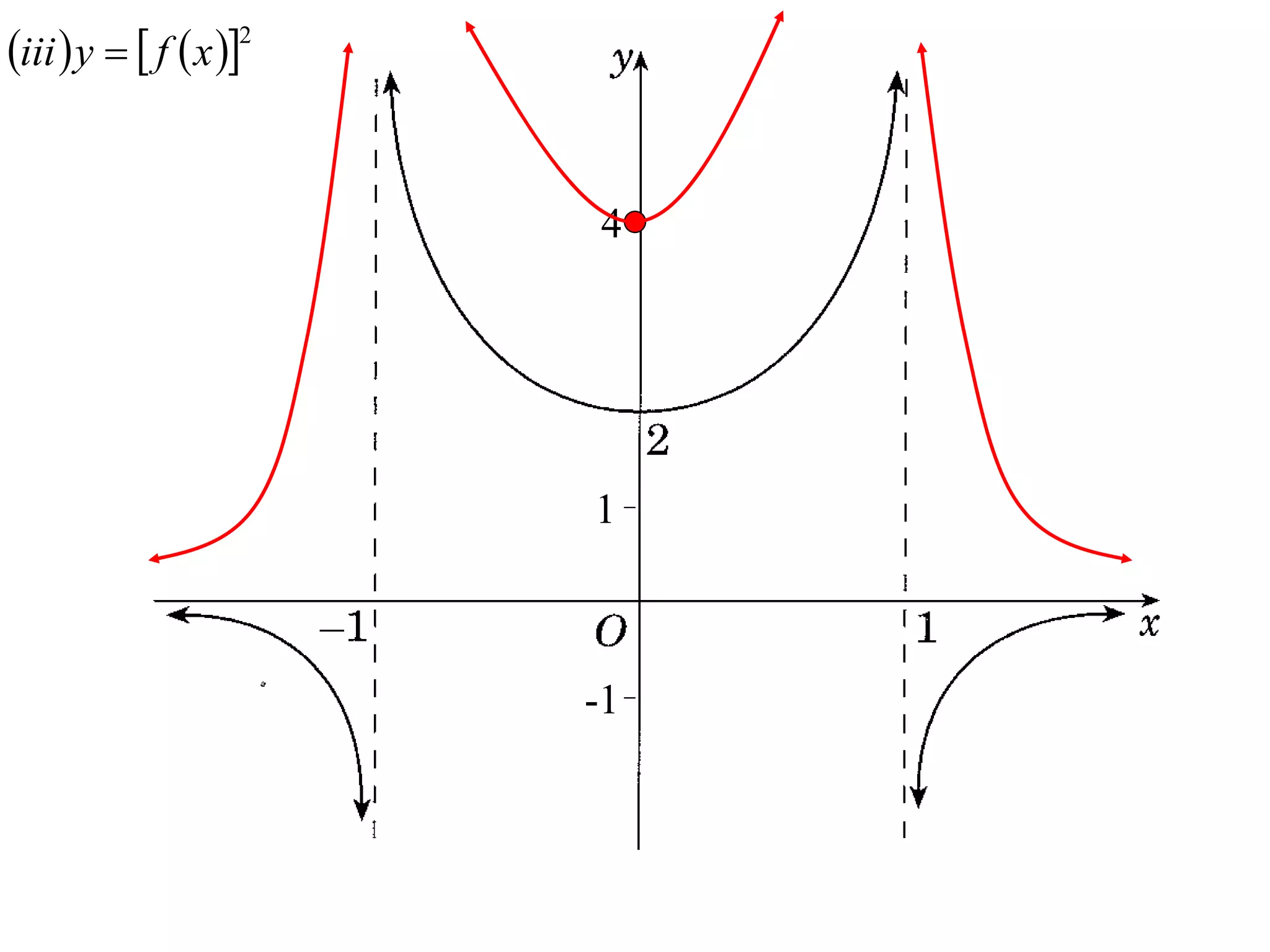
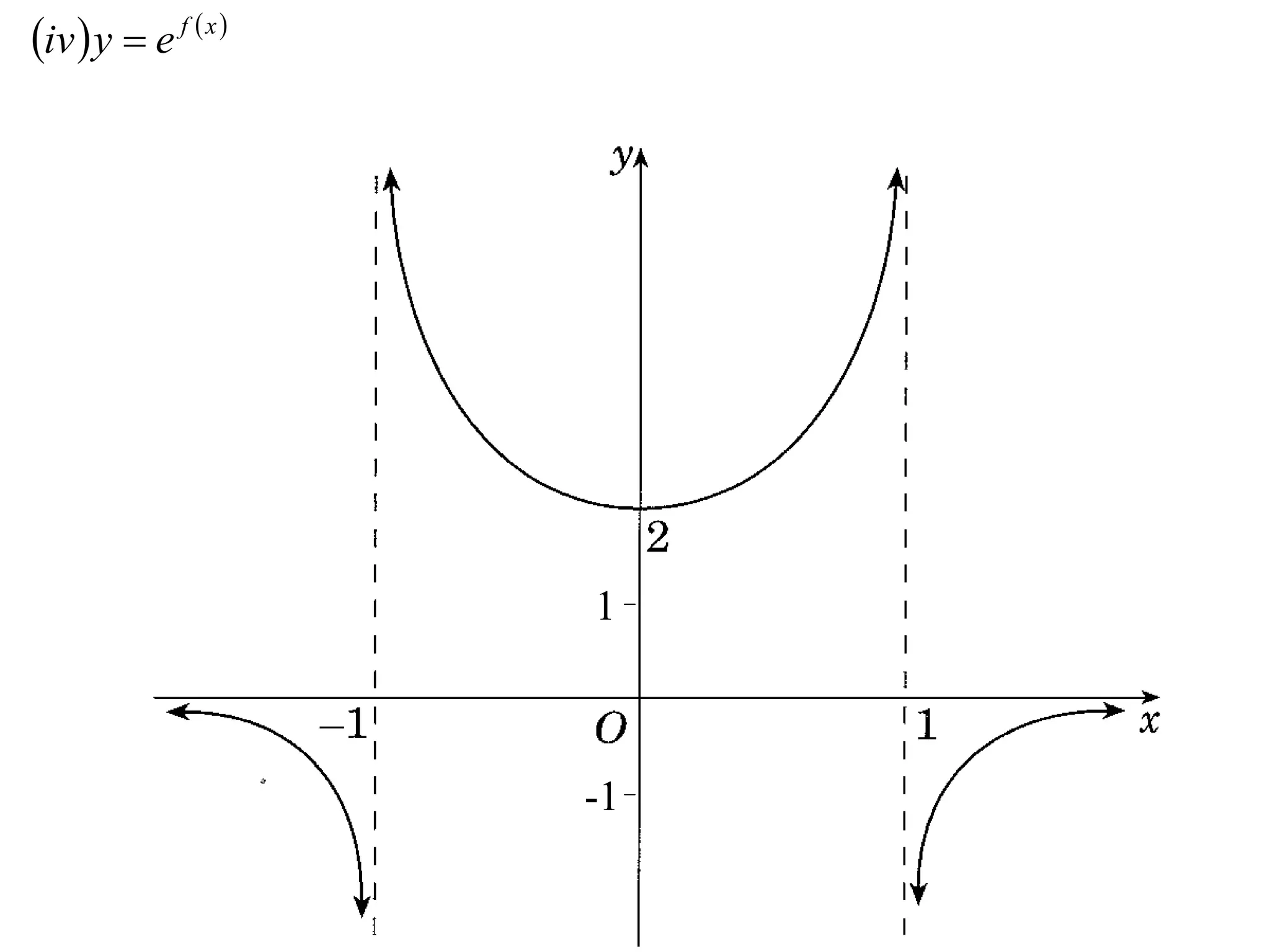
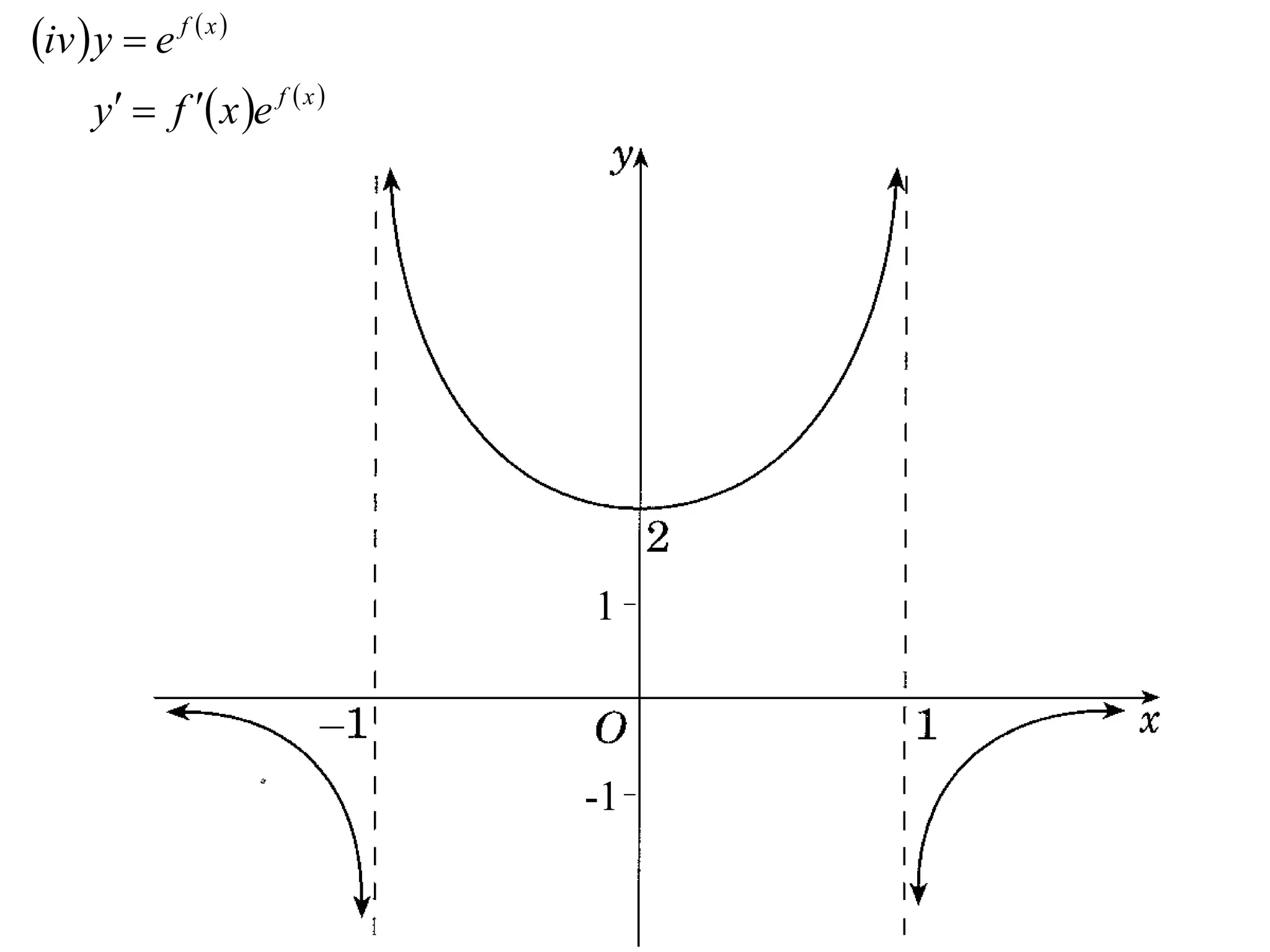
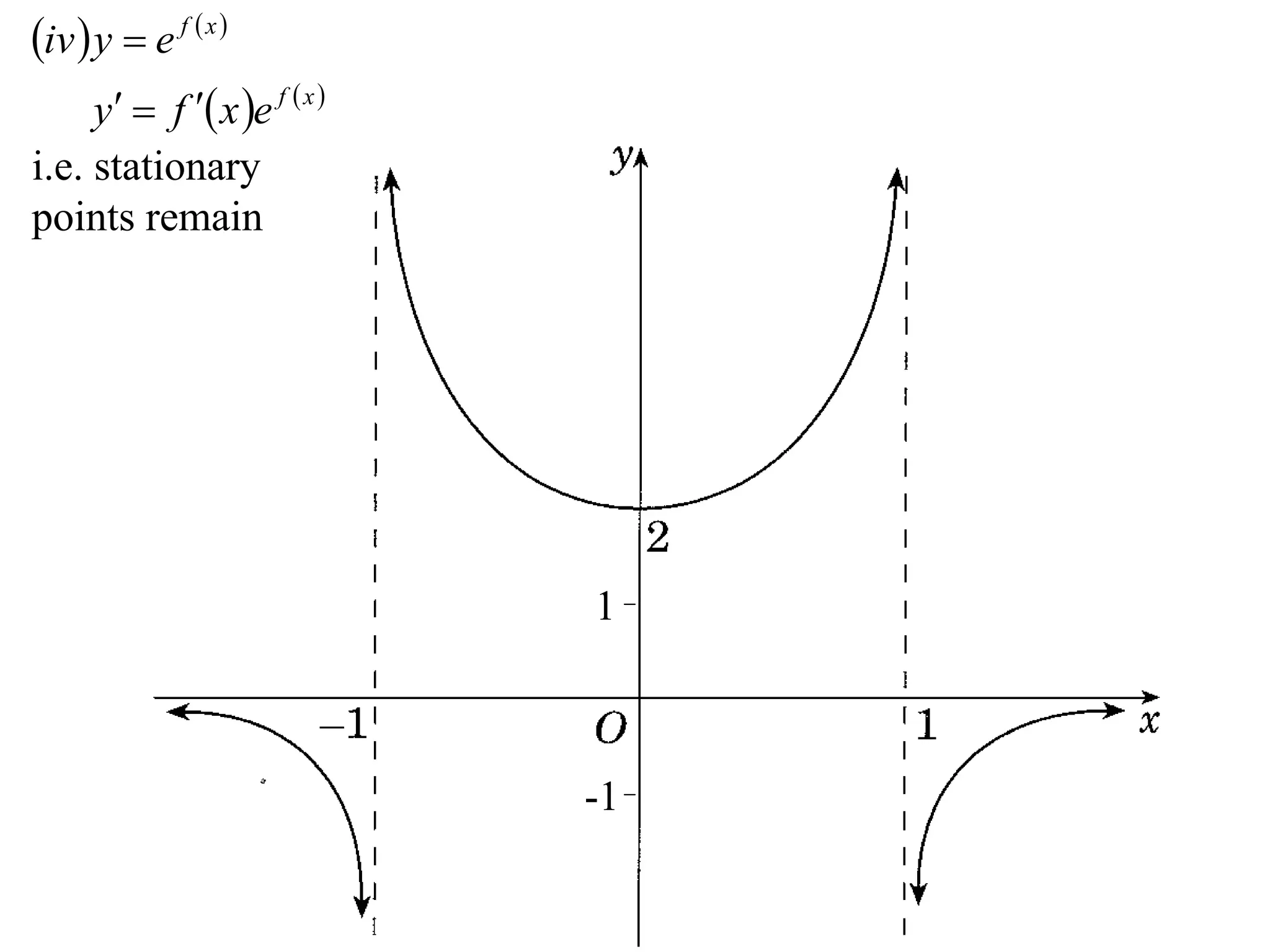
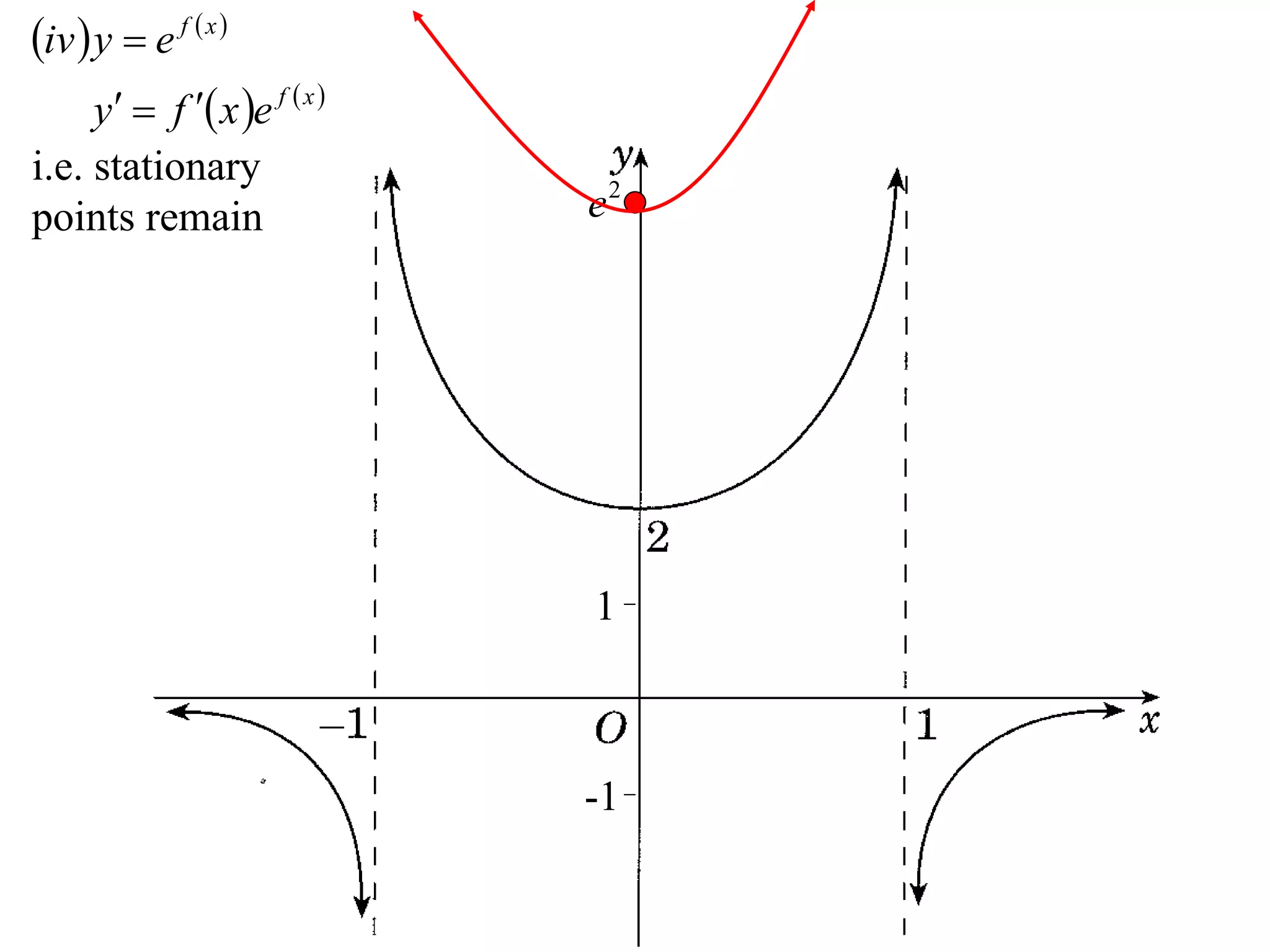
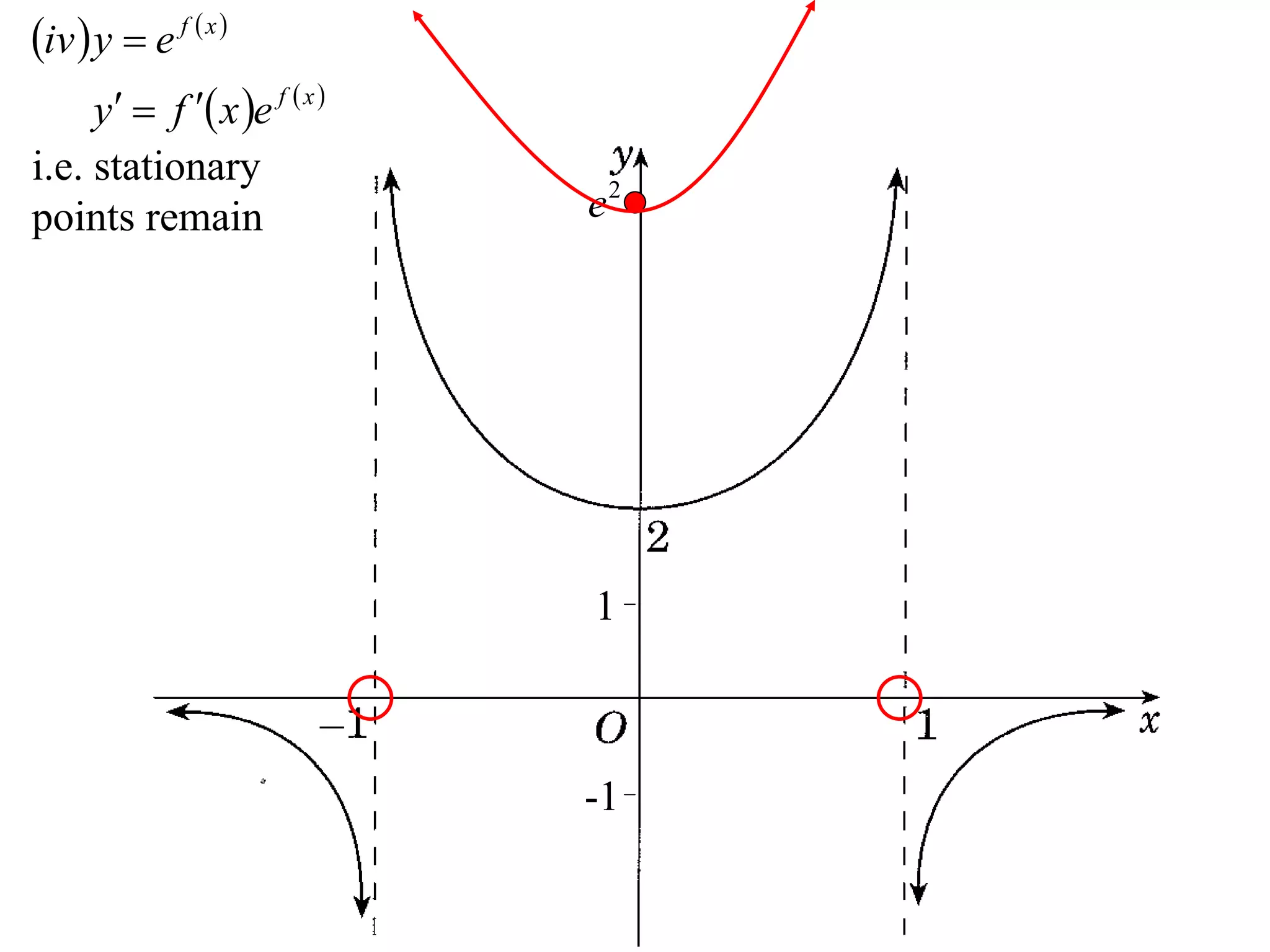
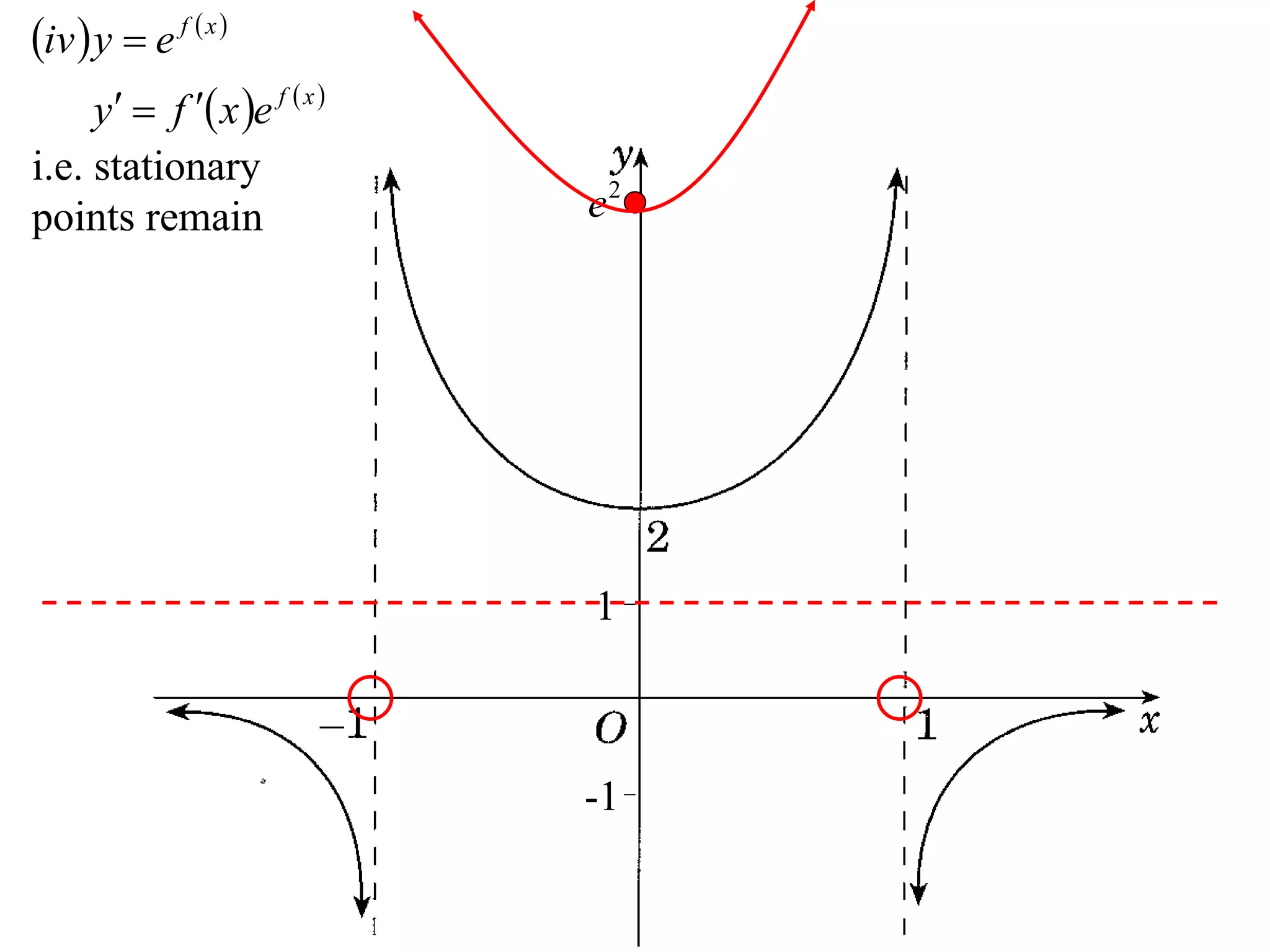
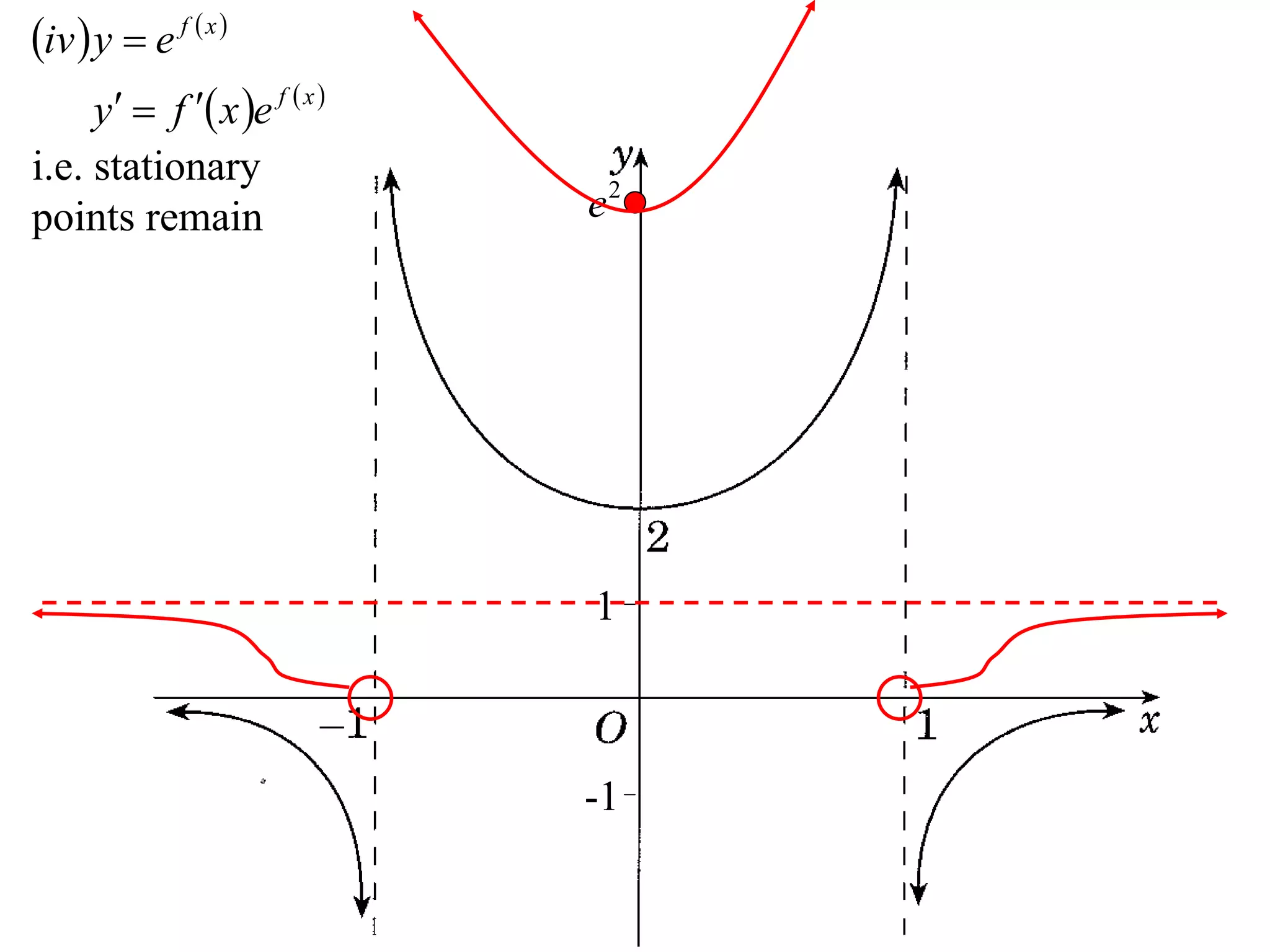
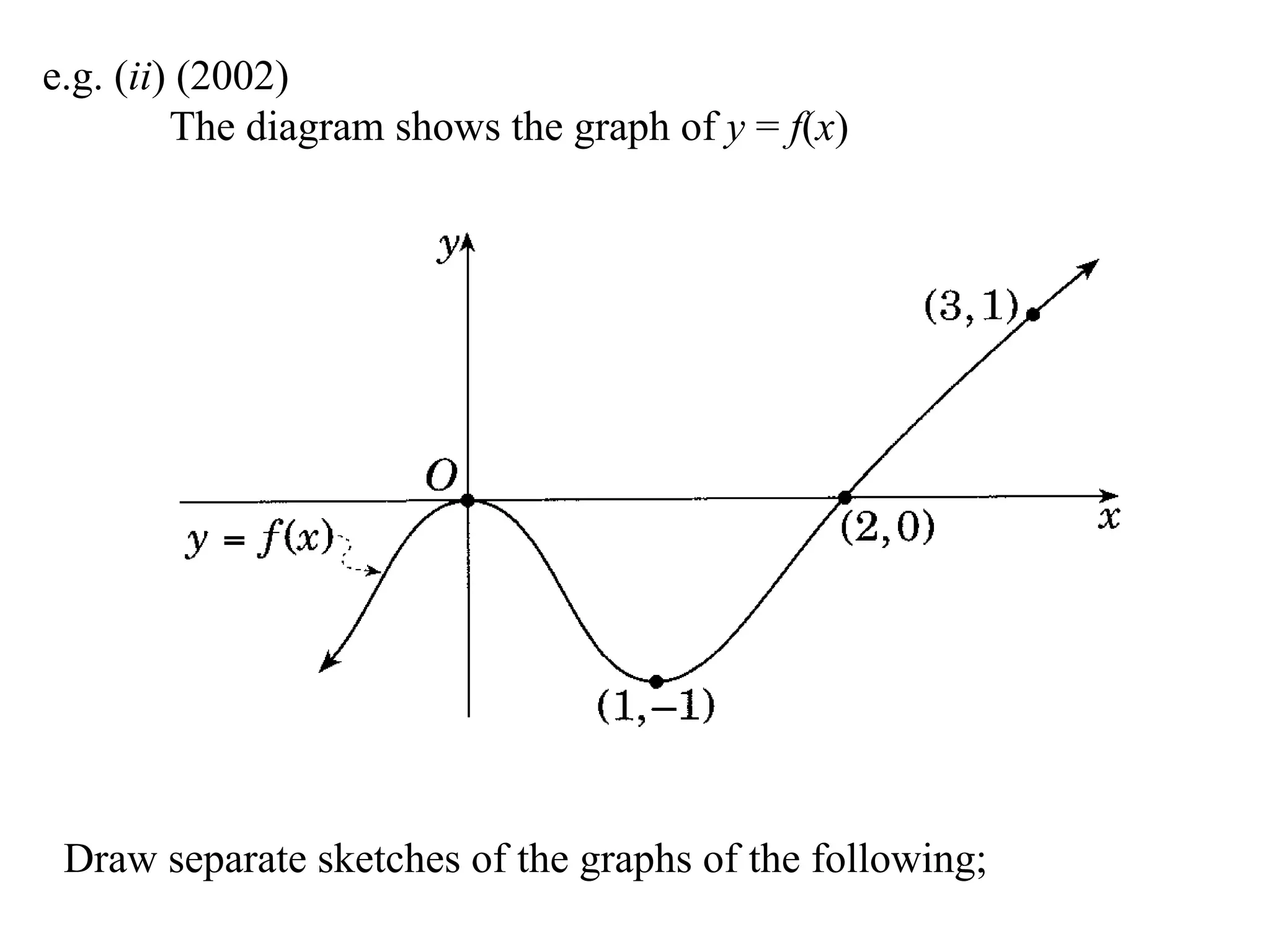
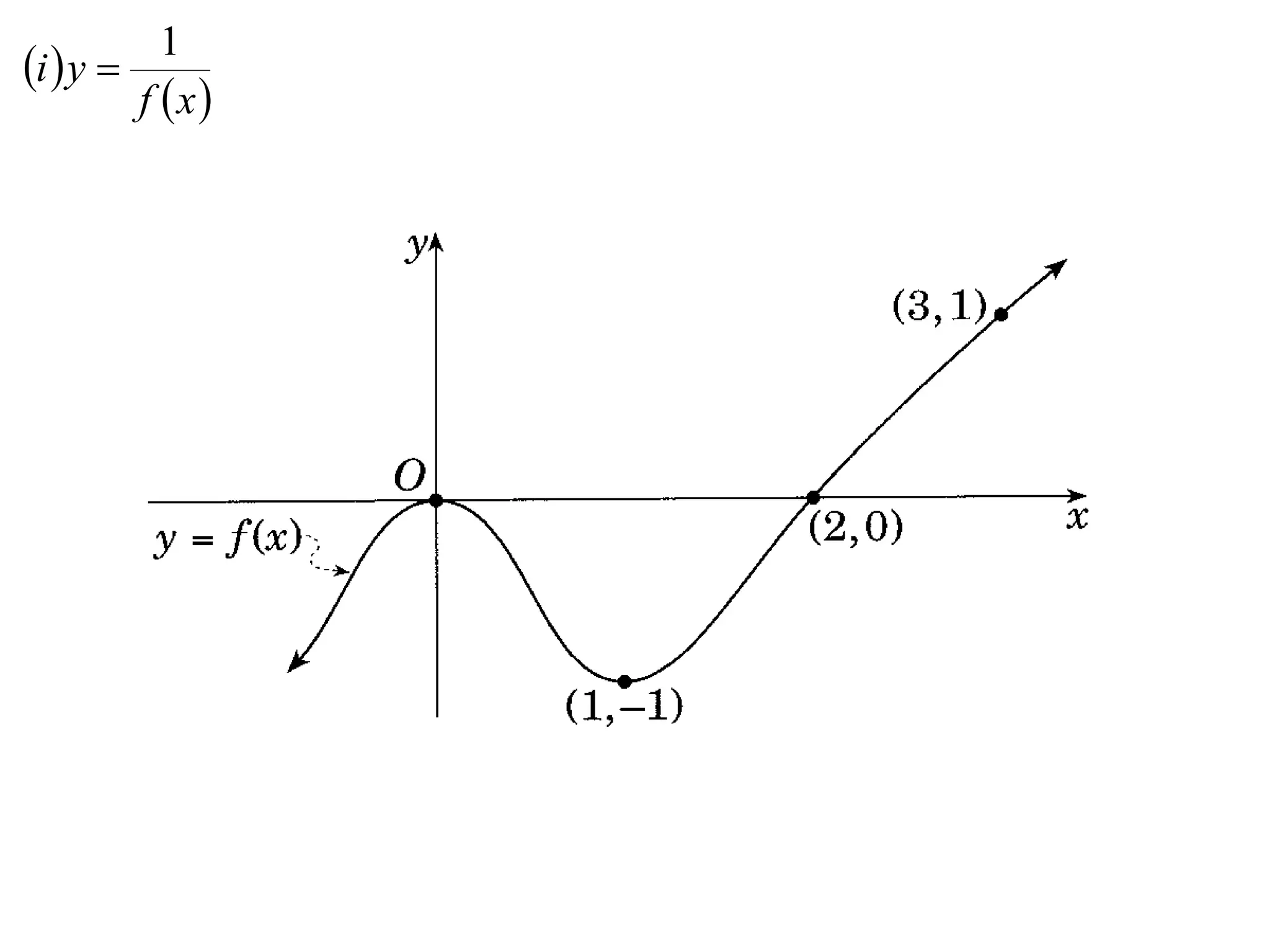
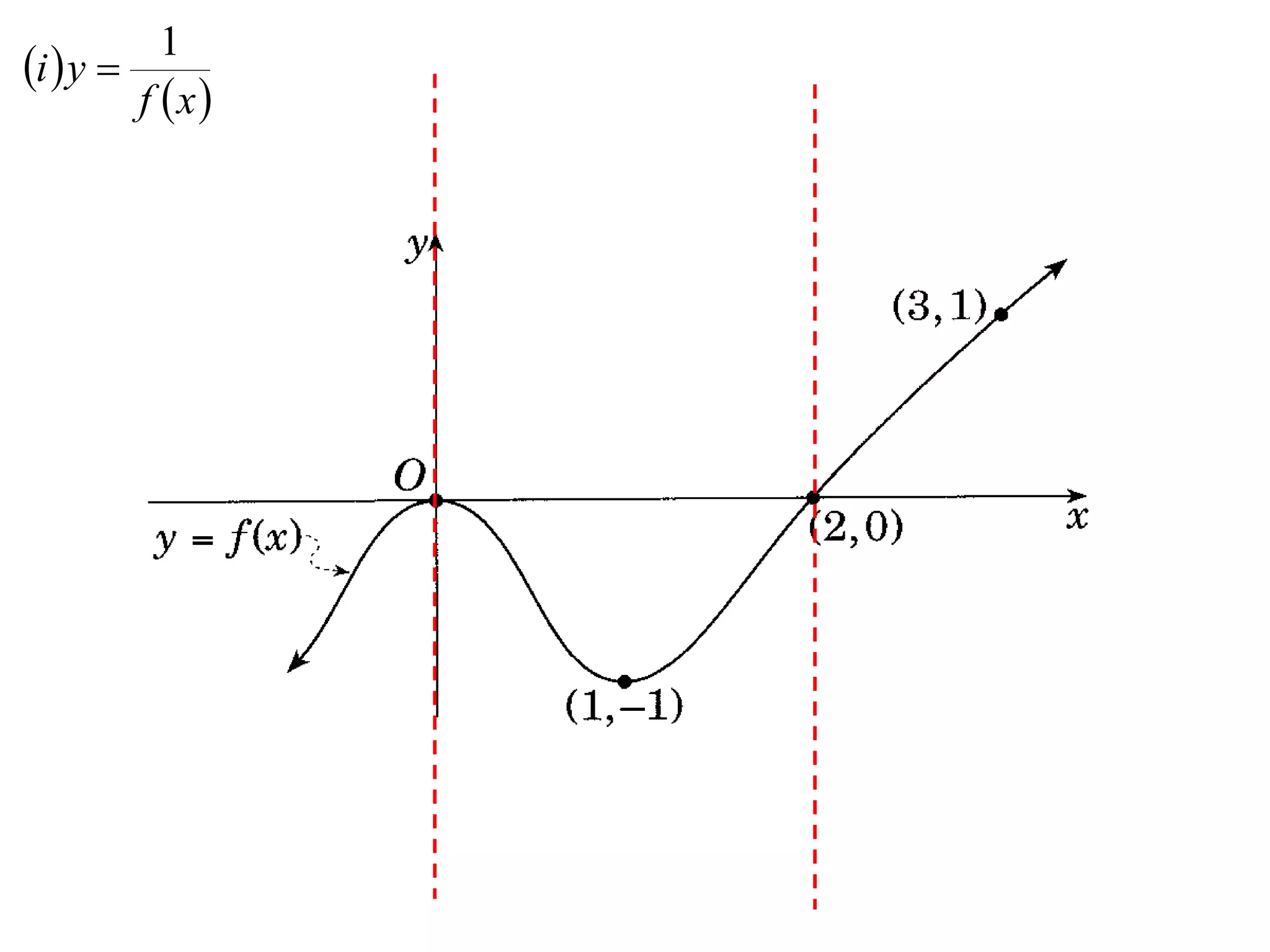
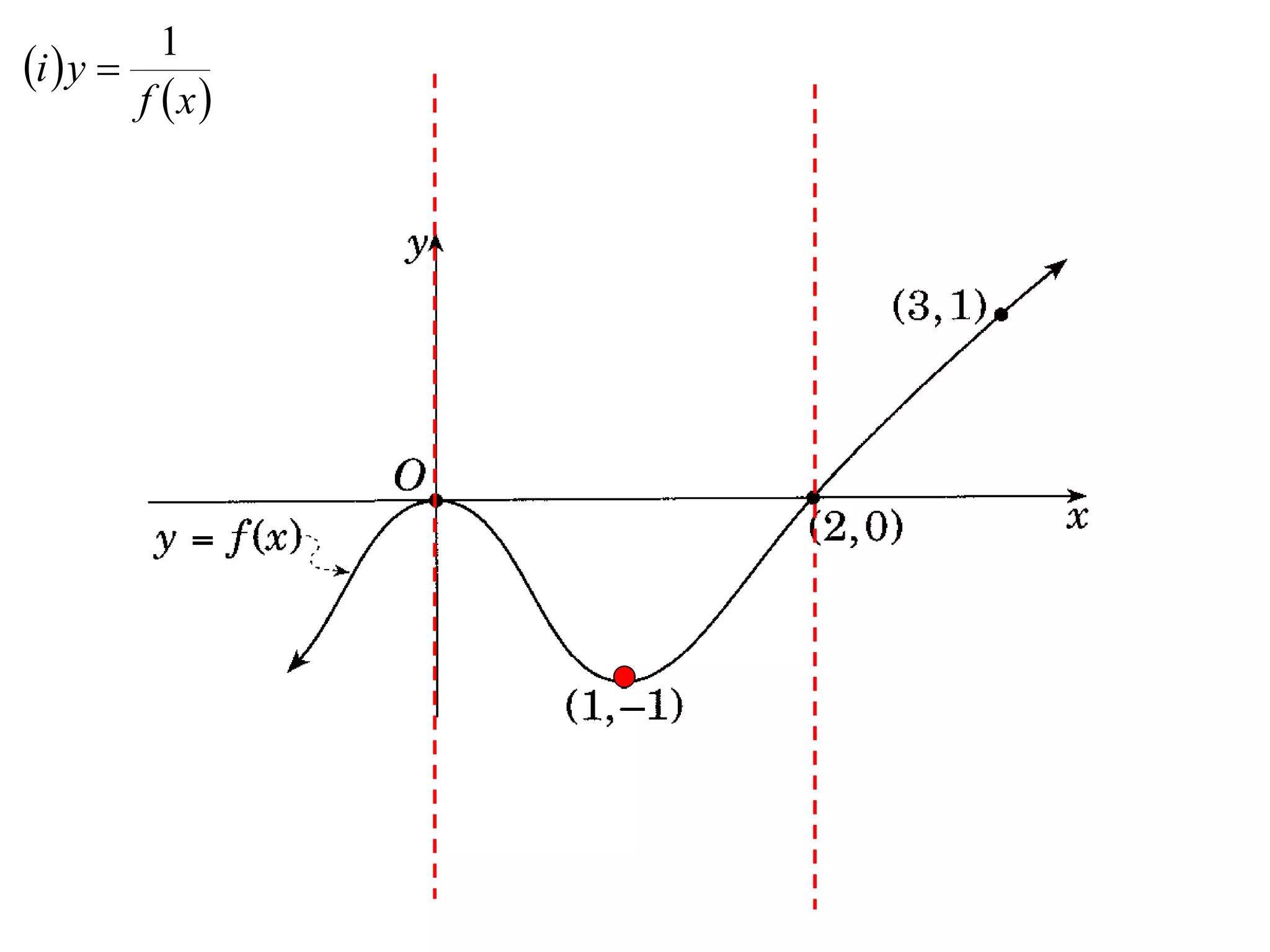
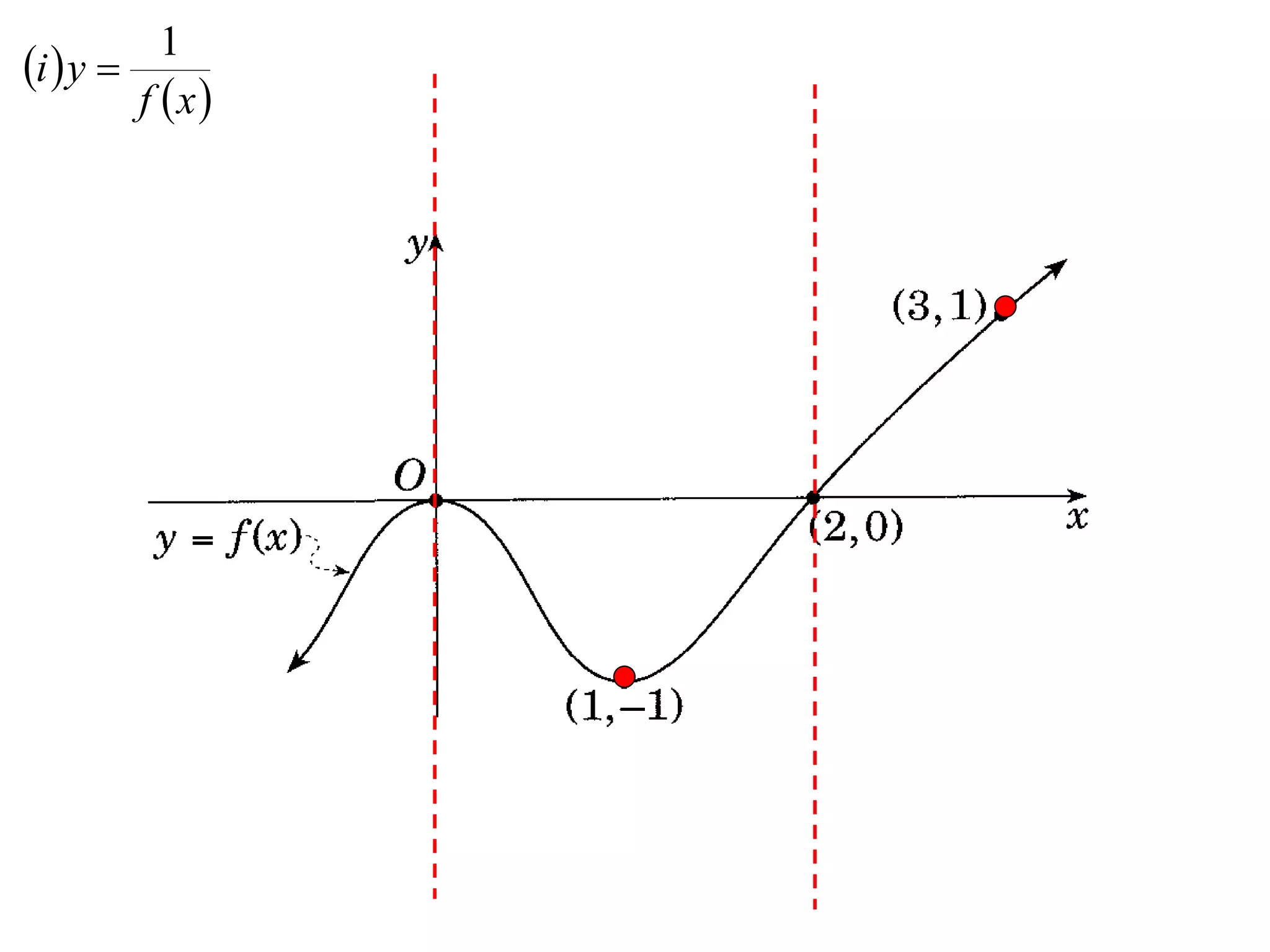
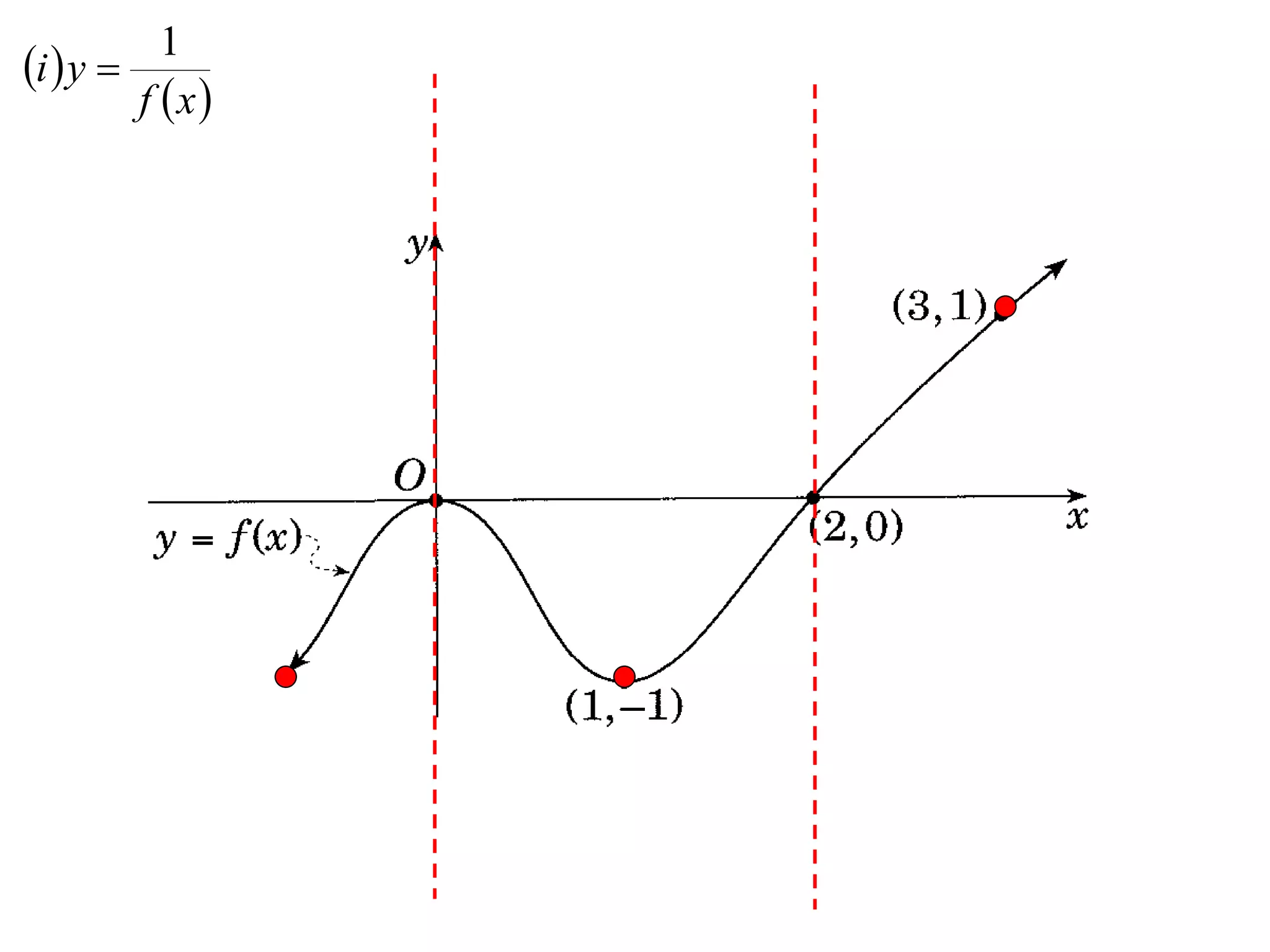
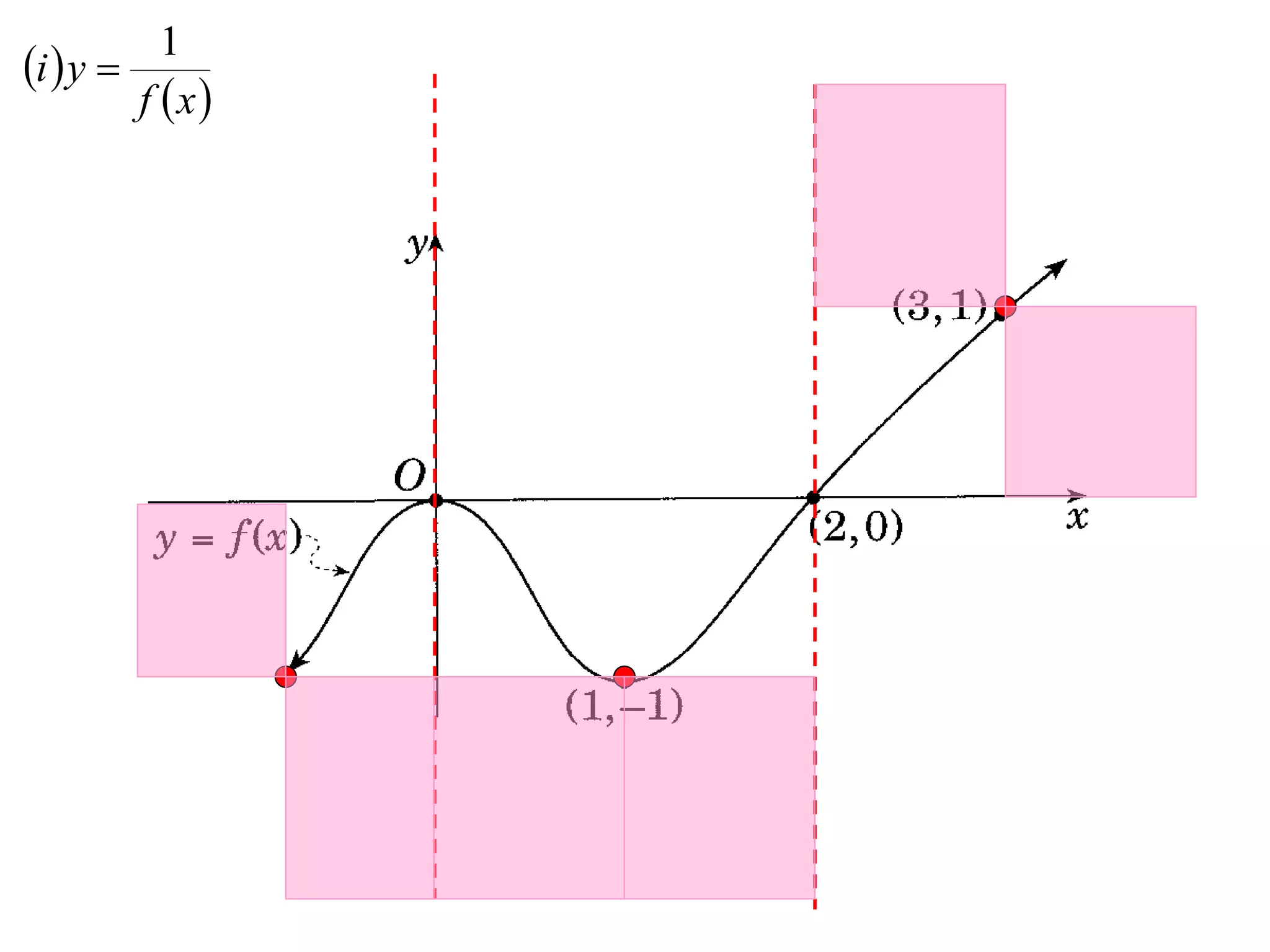
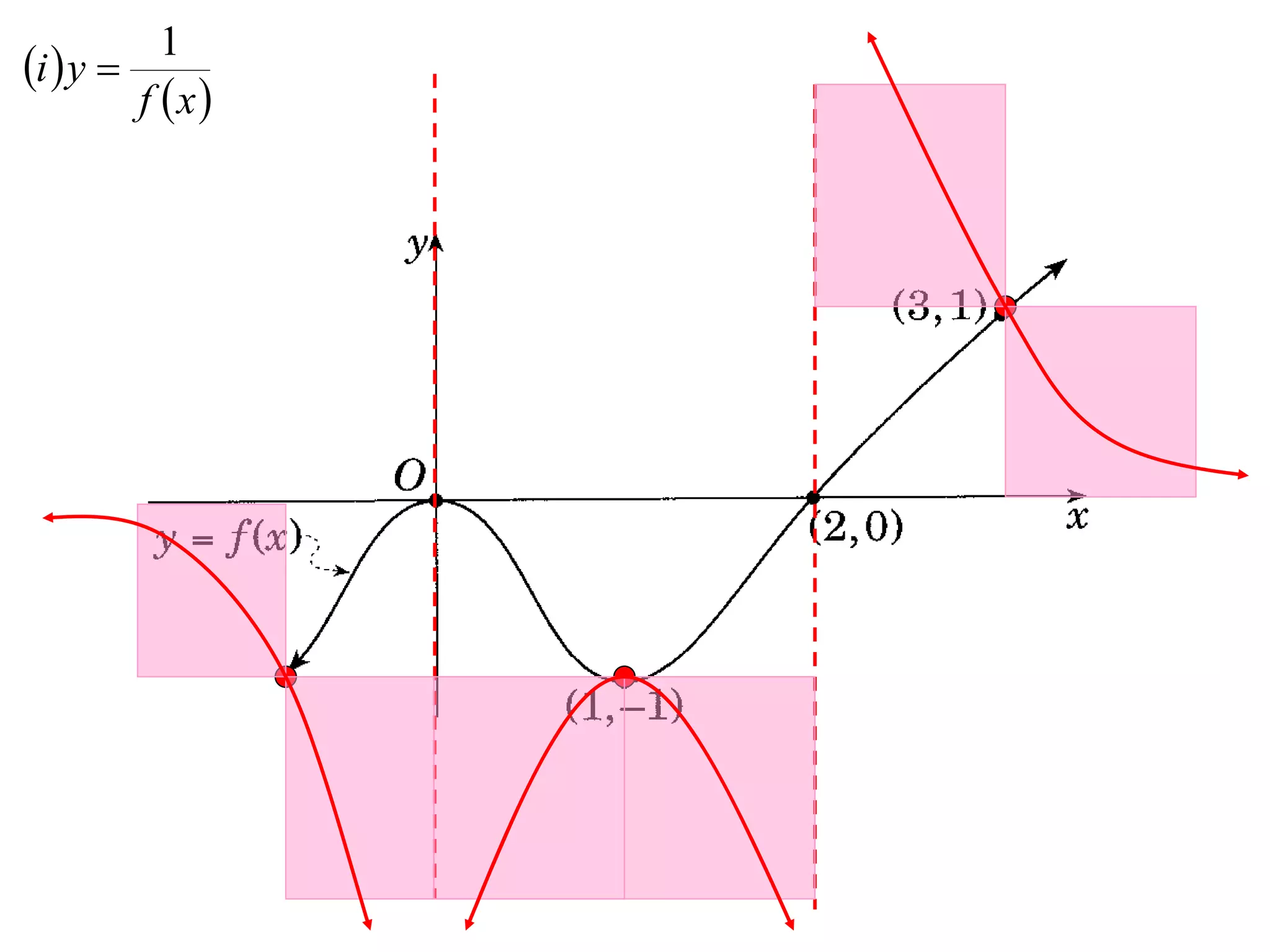
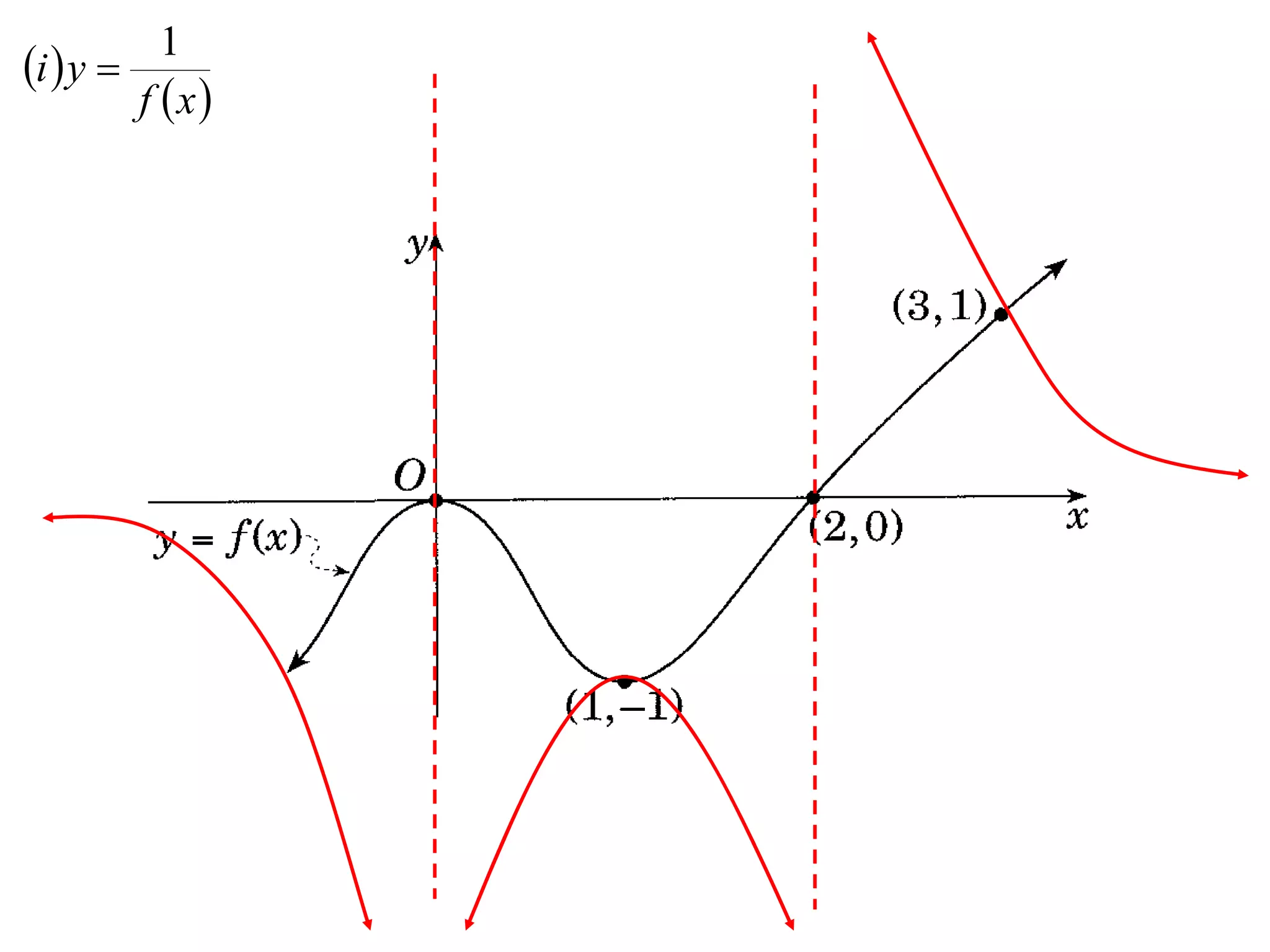
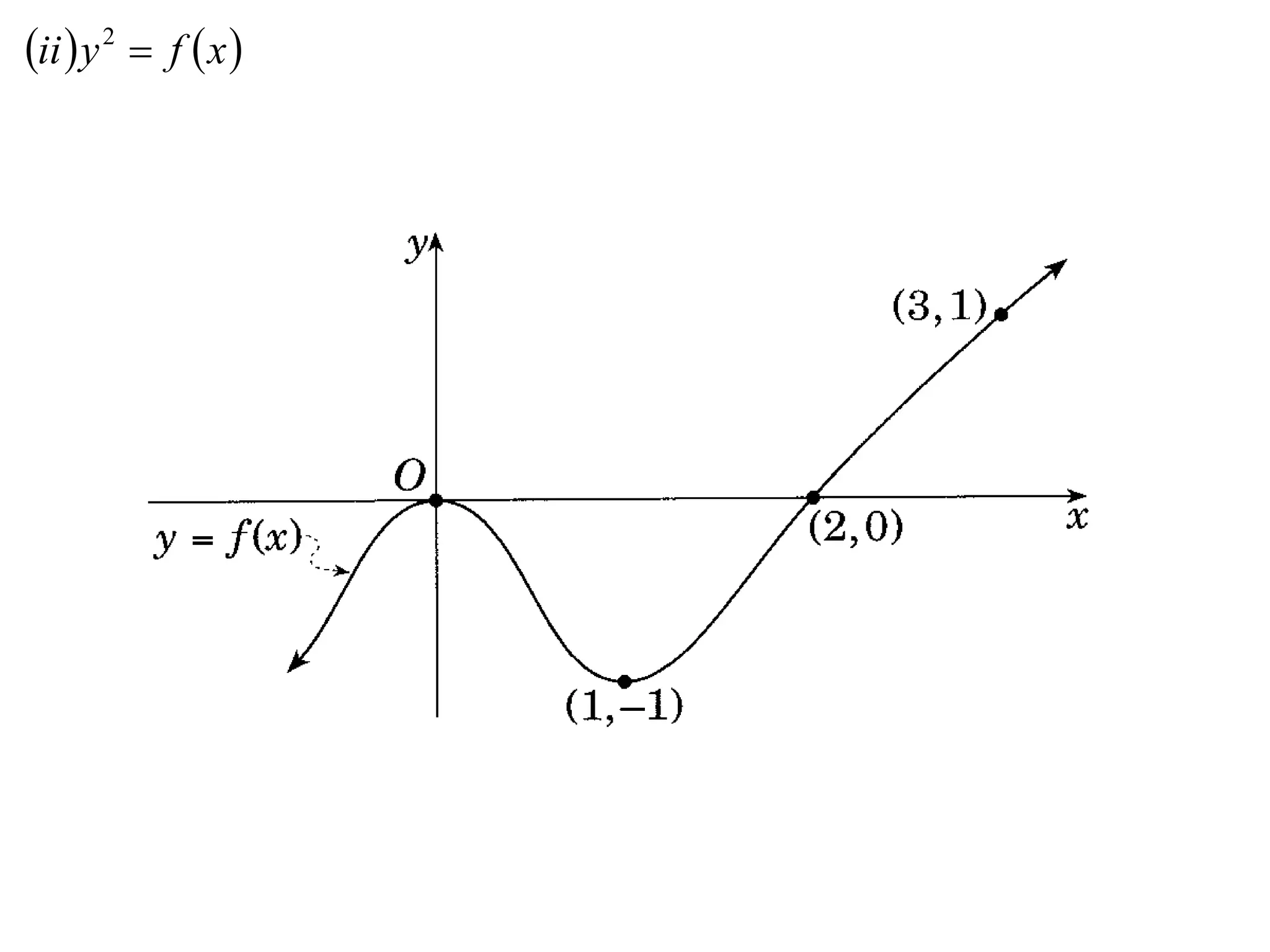
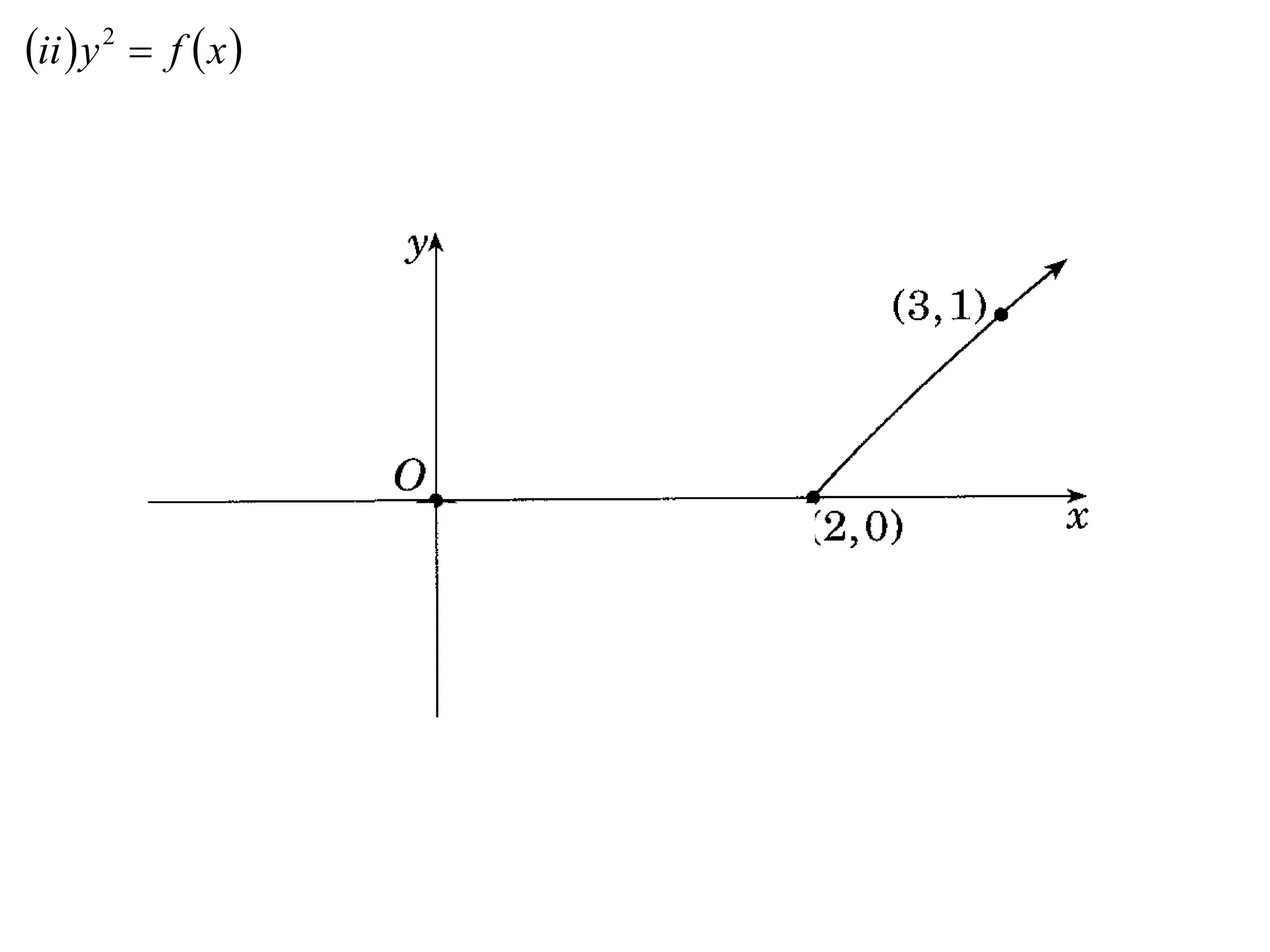
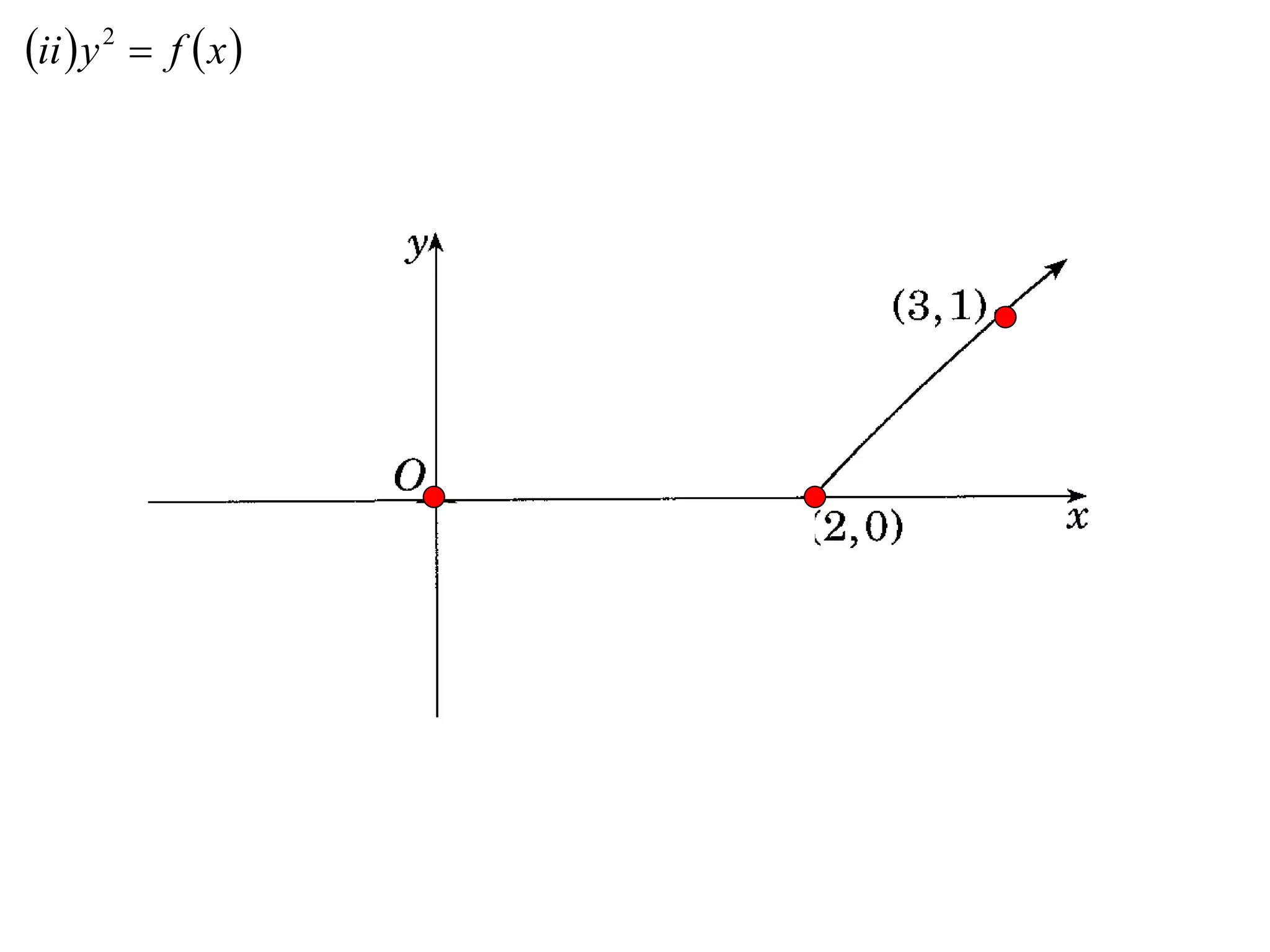
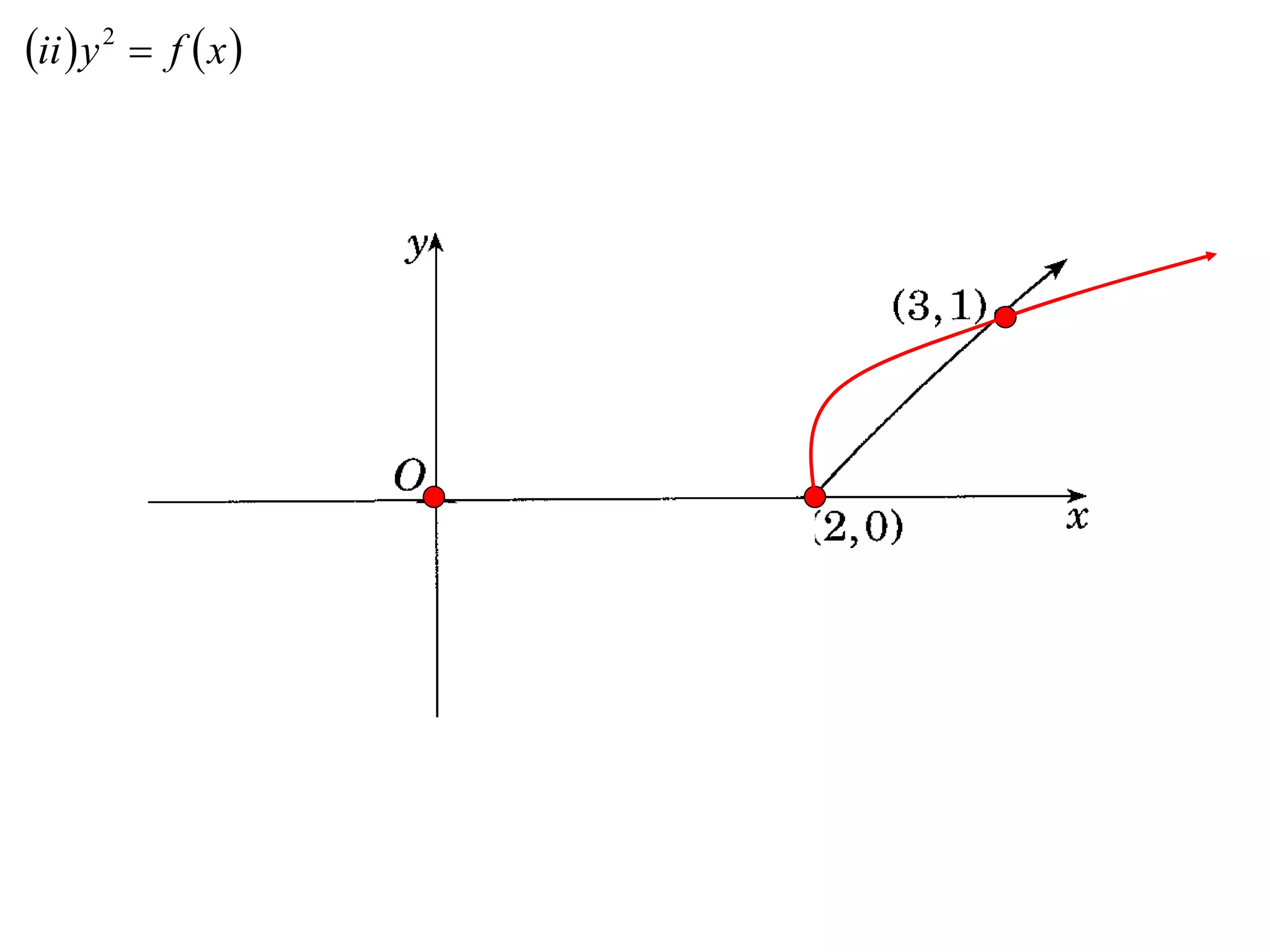
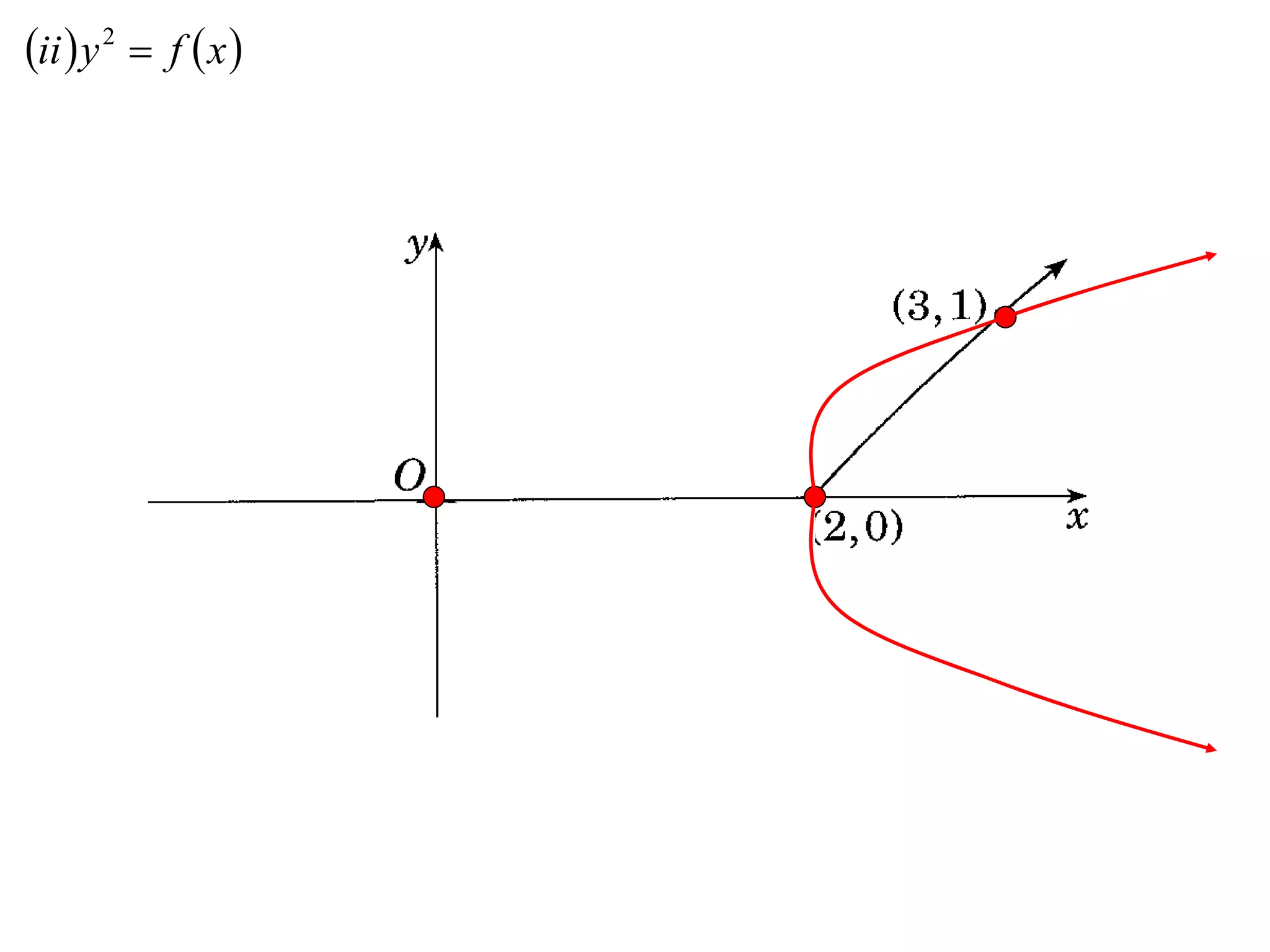
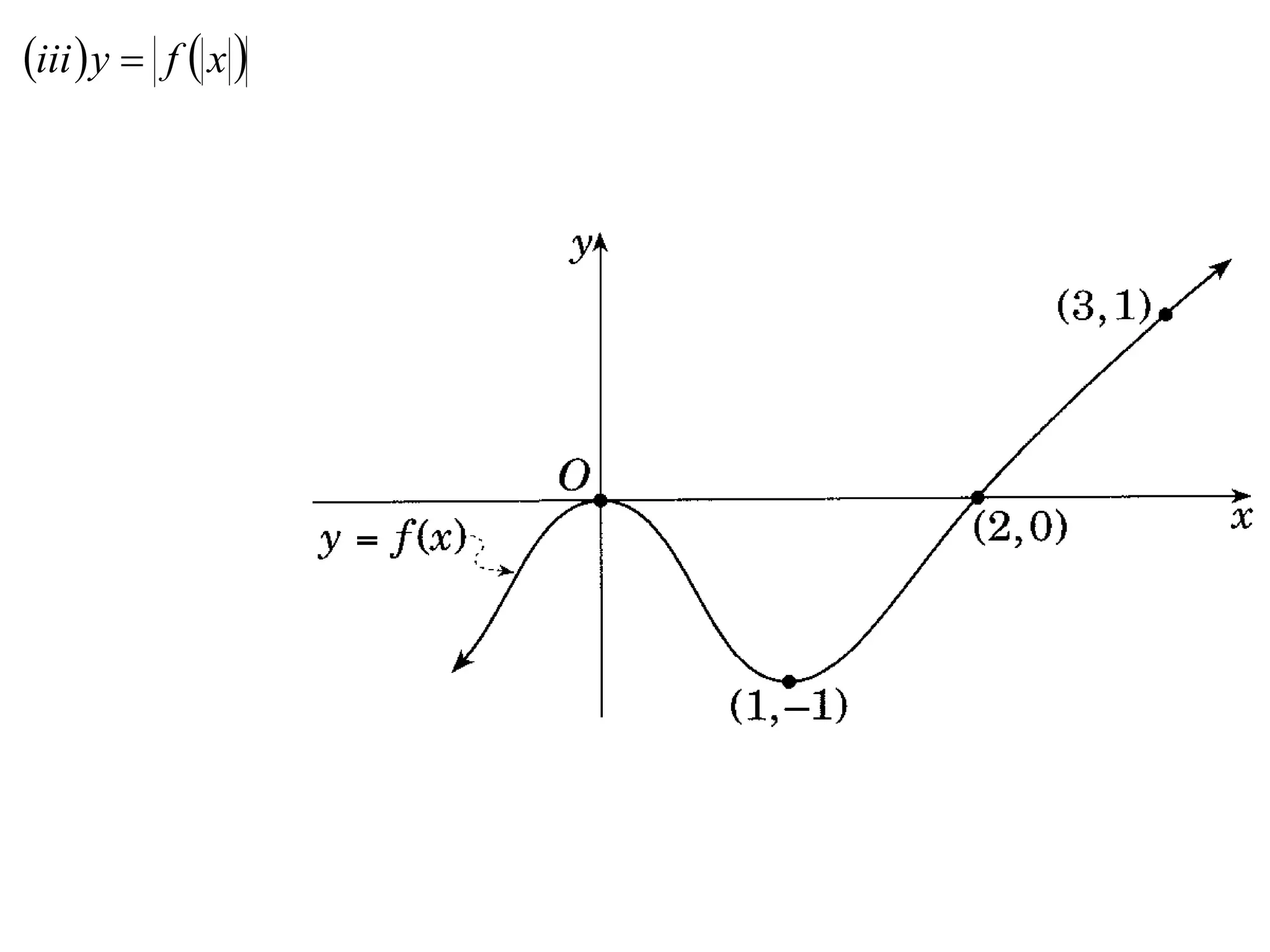
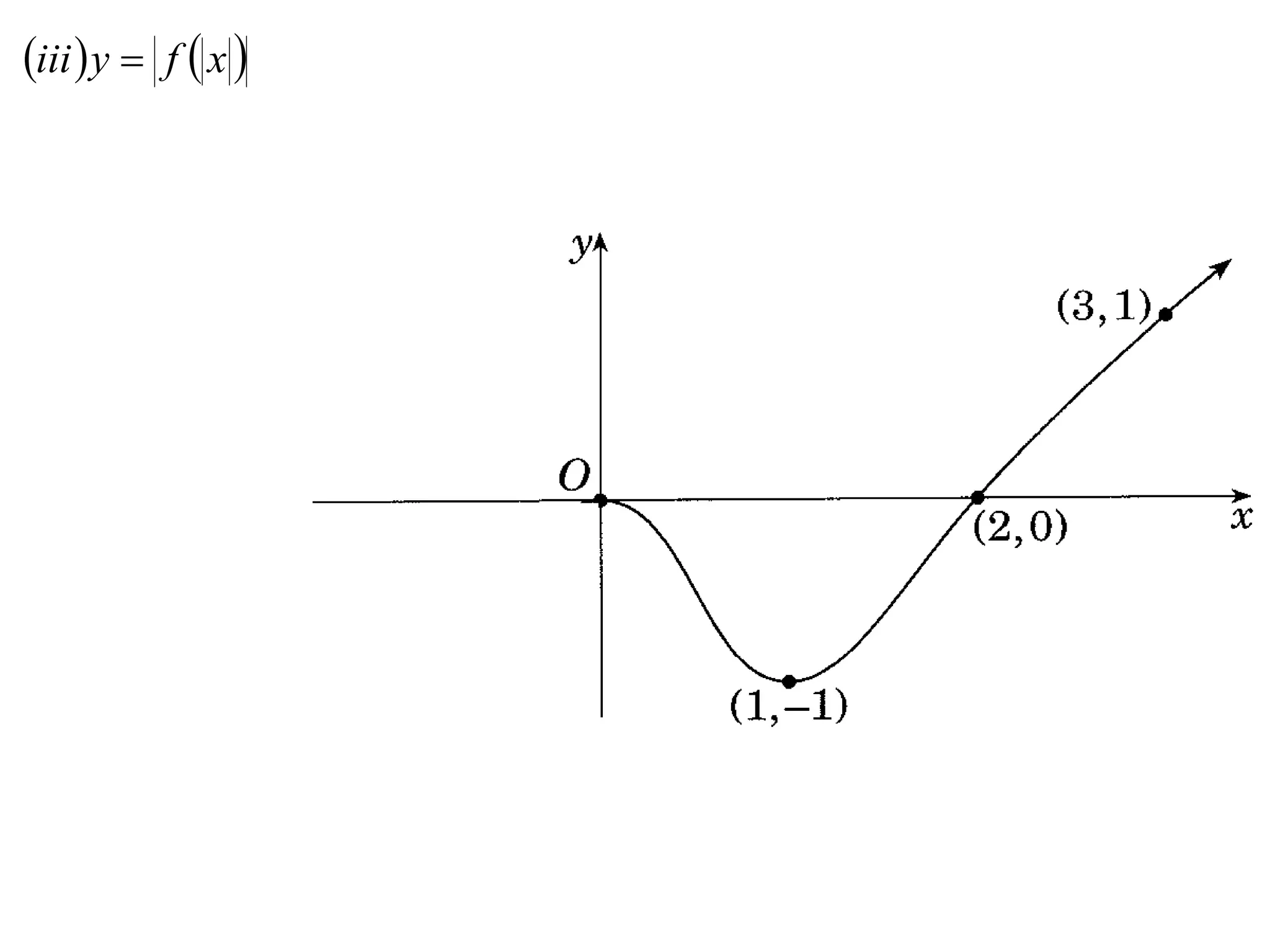
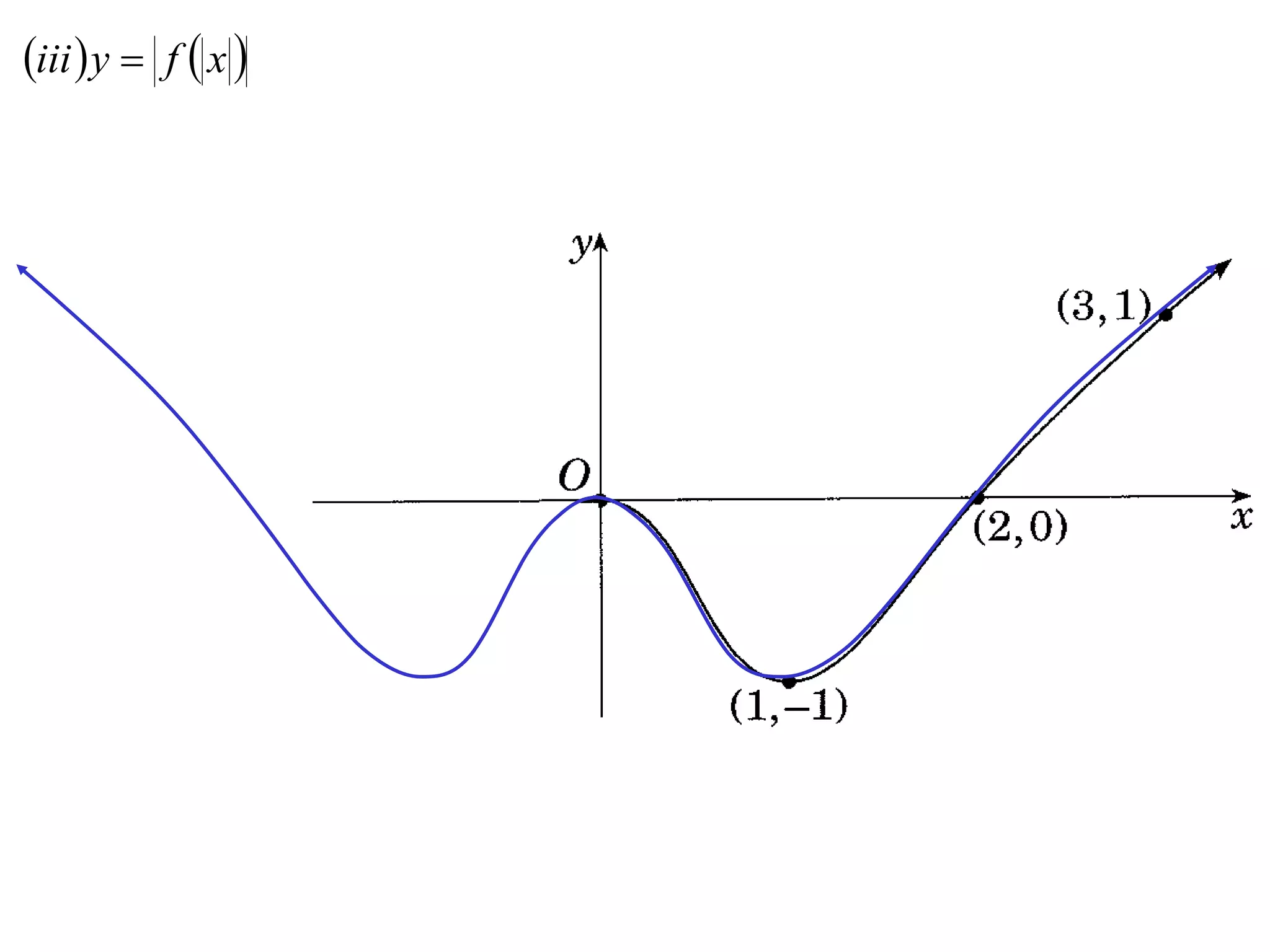
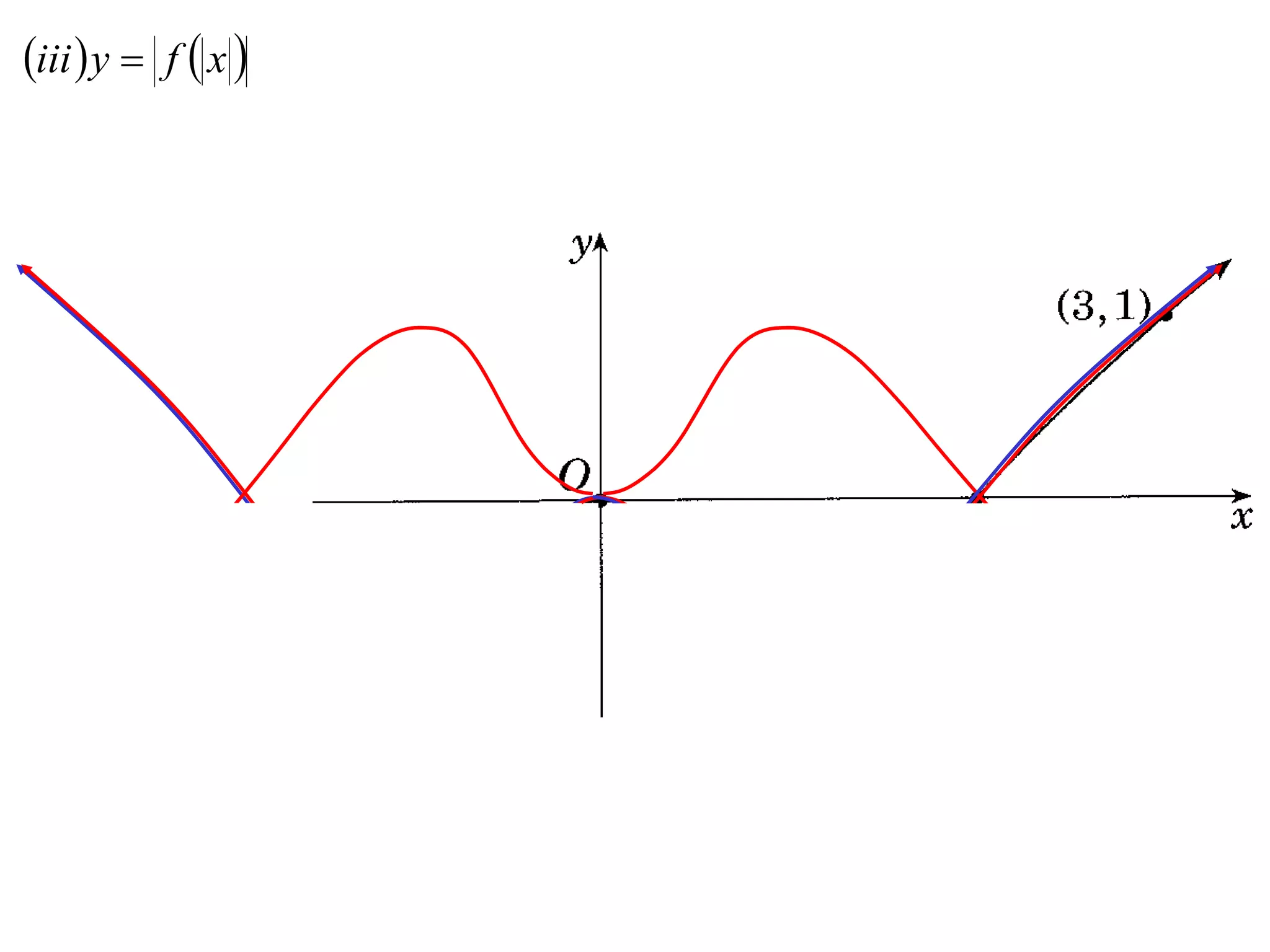
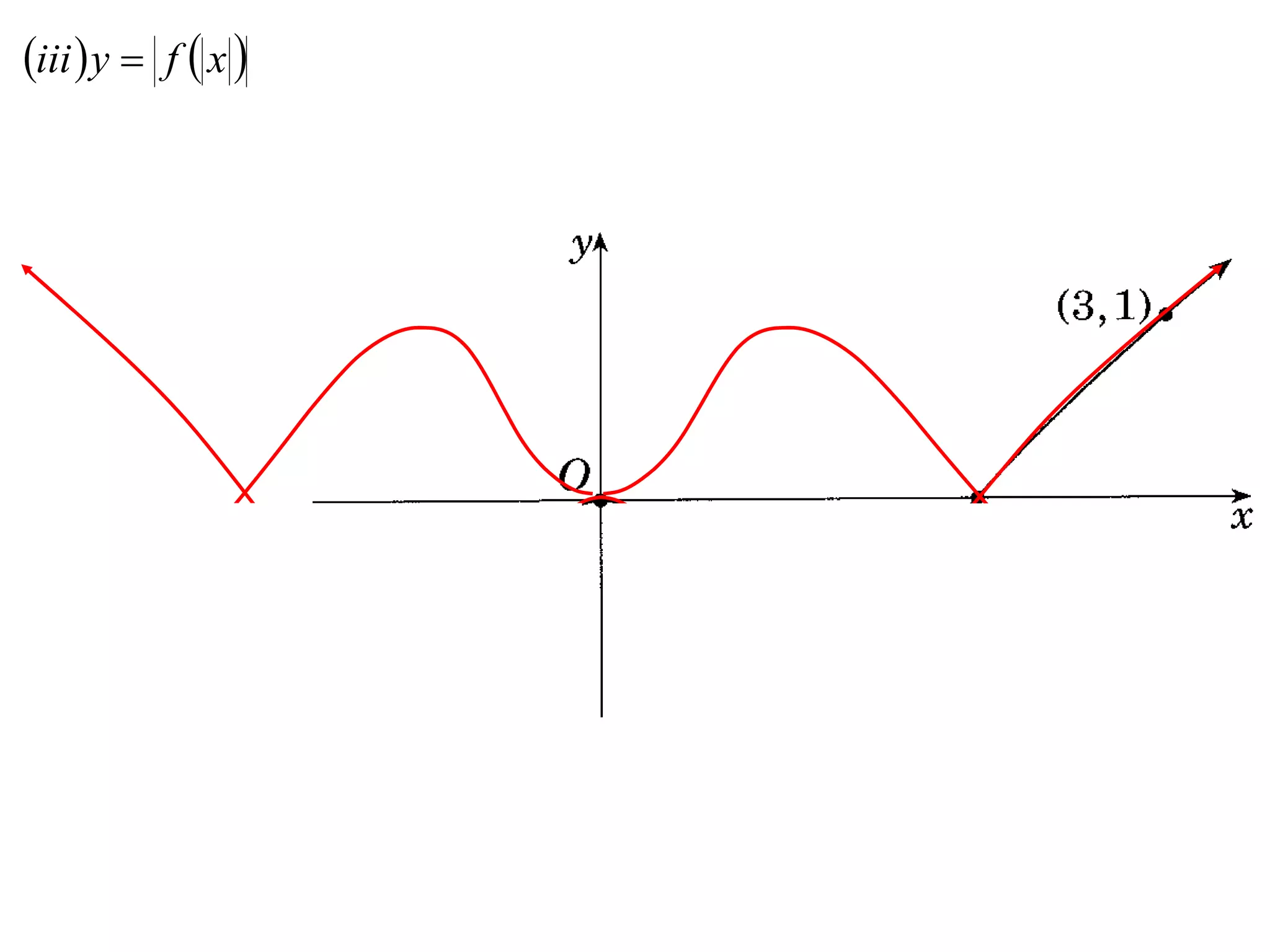
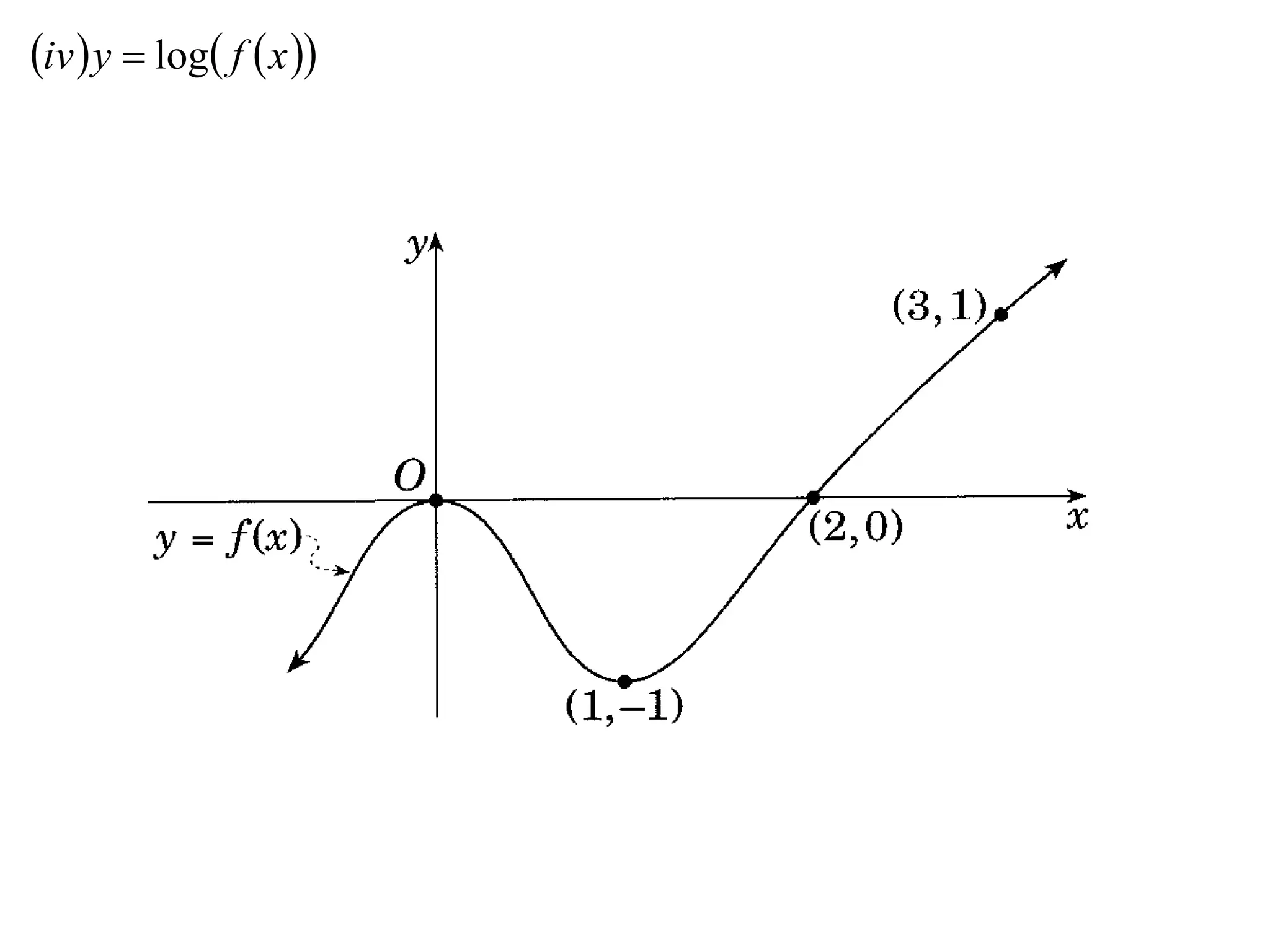
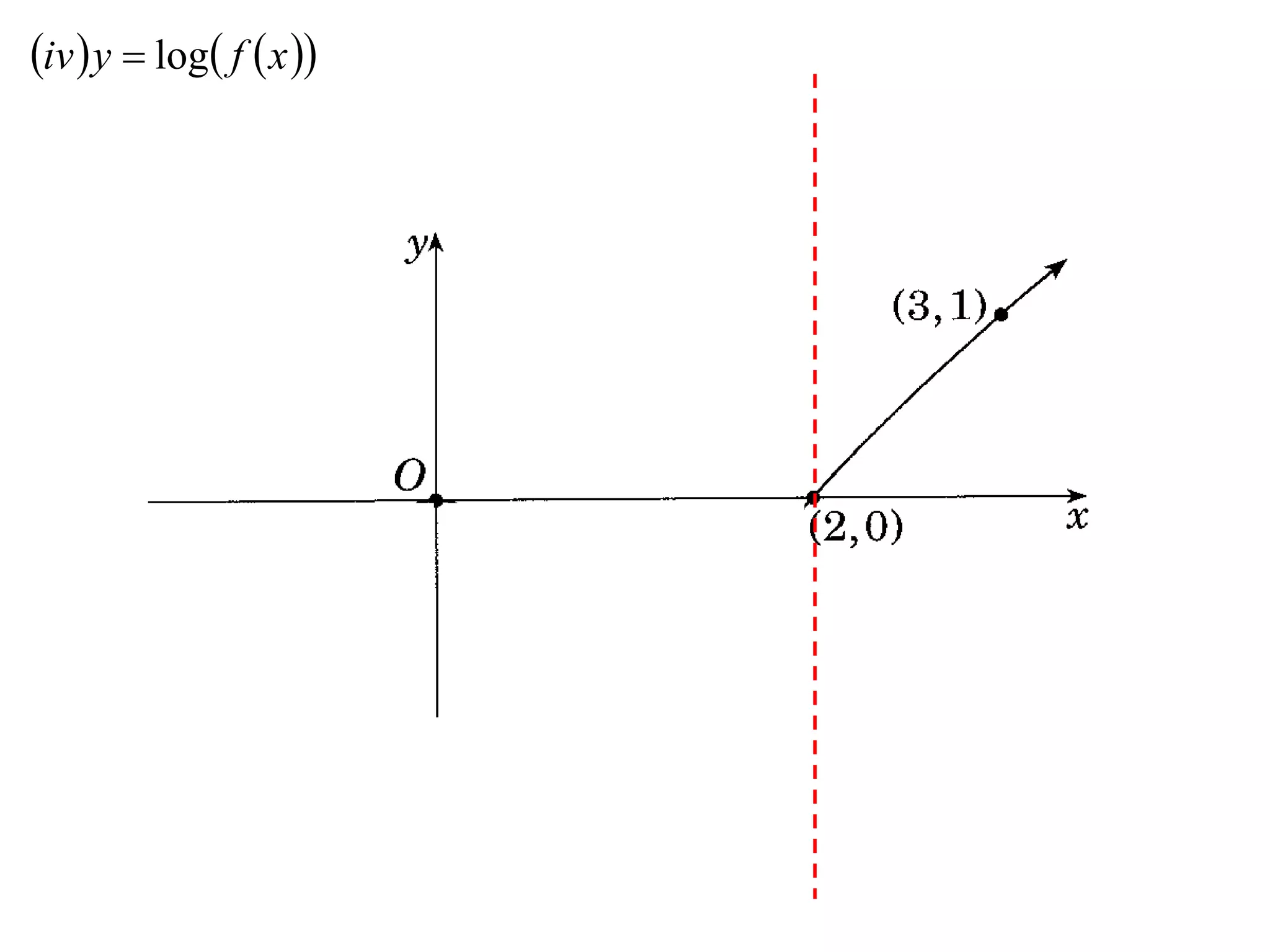
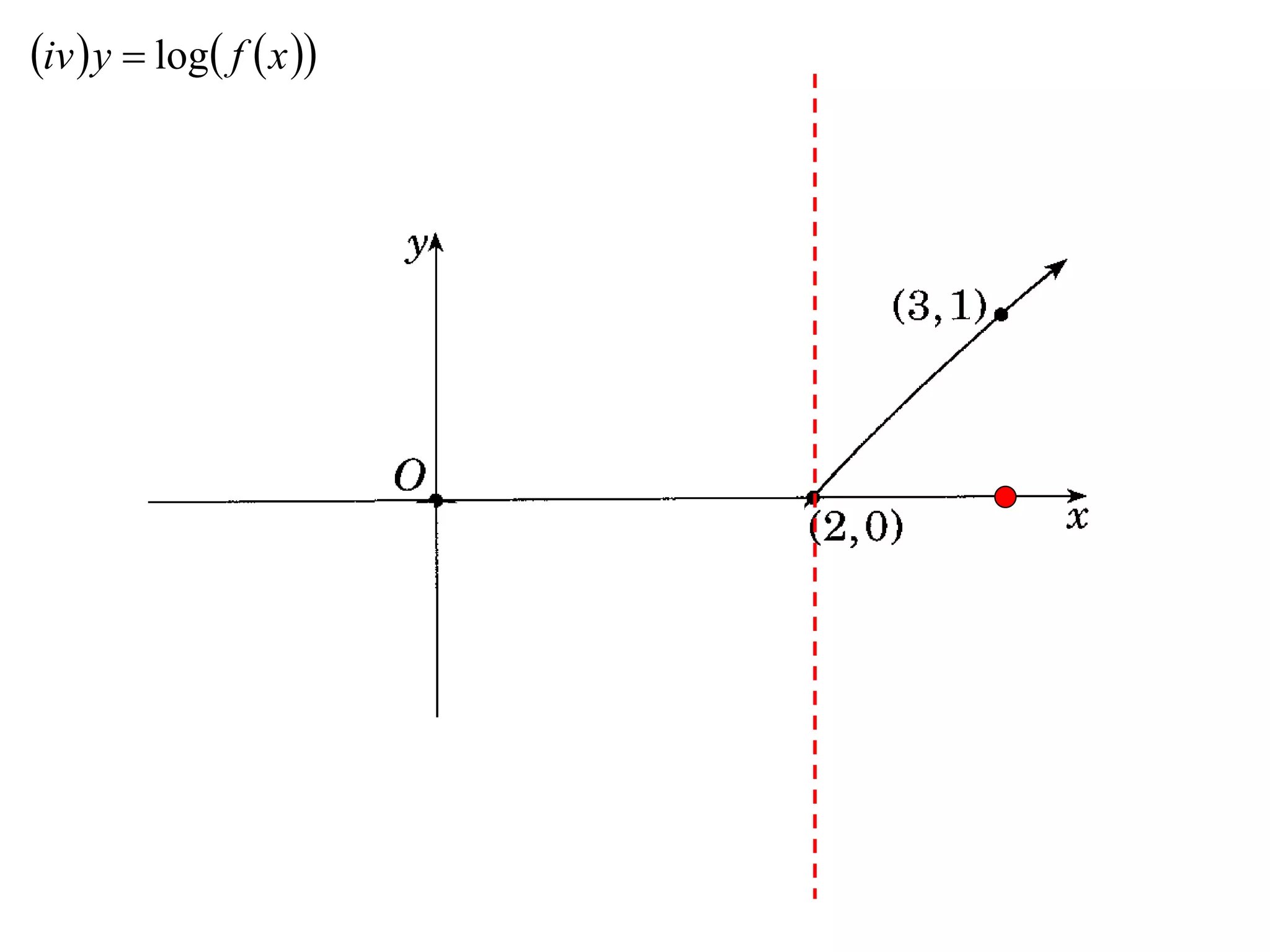
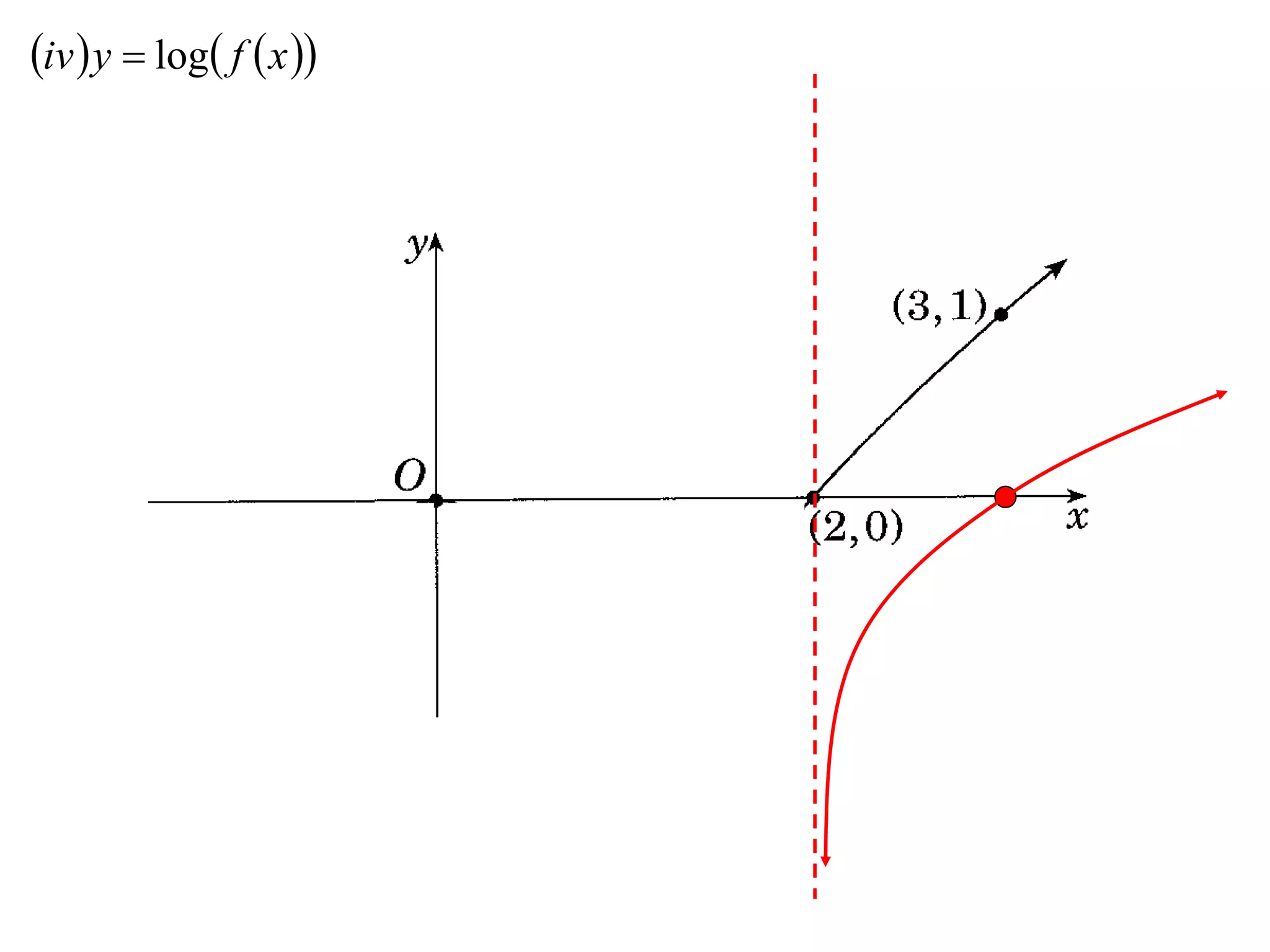
The document provides instructions to sketch the graphs of various functions, including y=f(x), y=f(x)+f(x), y=[f(x)]^2, y=e^f(x), and y=log(f(x)). It also includes examples of similar questions from past papers. The sketches are to be drawn separately for each function with labeled axes and key features like stationary points marked.

1. (J) Other Graphs
e.g. (i) (2003)
The diagram shows the graph of y = f(x)
Draw separate sketches of the graphs of the following;

2. 1
i  y 
f x

3. 1
i  y 
f x
1
-1

4. 1
i  y 
f x
1
-1

5. 1
i  y 
f x
1
-1

6. 1
i  y 
f x
1
1
2
-1

7. 1
i  y 
f x
1
1
2
-1

8. ii  y  f  x   f  x 
1
-1

9. ii  y  f  x   f  x 
1
-1

10. ii  y  f  x   f  x 
4
1
-1

11. ii  y  f  x   f  x 
4
1
-1

12. ii  y  f  x   f  x 
4
1
-1

13. iii  y   f  x 2
1
-1

14. iii  y   f  x 2
4
1
-1

15. iii  y   f  x 2
4
1
-1

16. iii  y   f  x 2
4
1
-1

17. iv  y  e f  x 
1
-1

18. iv  y  e f  x 
y  f  x e f  x 
1
-1

19. iv  y  e f  x 
y  f  x e f  x 
i.e. stationary
points remain
1
-1

20. iv  y  e f  x 
y  f  x e f  x 
i.e. stationary
points remain e2
1
-1

21. iv  y  e f  x 
y  f  x e f  x 
i.e. stationary
points remain e2
1
-1

22. iv  y  e f  x 
y  f  x e f  x 
i.e. stationary
points remain e2
1
-1

23. iv  y  e f  x 
y  f  x e f  x 
i.e. stationary
points remain e2
1
-1

24. iv  y  e f  x 
y  f  x e f  x 
i.e. stationary
points remain e2
1
-1

25. e.g. (ii) (2002)
The diagram shows the graph of y = f(x)
Draw separate sketches of the graphs of the following;

26. 1
i  y 
f x

27. 1
i  y 
f x

28. 1
i  y 
f x

29. 1
i  y 
f x

30. 1
i  y 
f x

31. 1
i  y 
f x

32. 1
i  y 
f x

33. 1
i  y 
f x

34. ii  y 2  f  x 

35. ii  y 2  f  x 

36. ii  y 2  f  x 

37. ii  y 2  f  x 

38. ii  y 2  f  x 

39. iii  y  f  x 

40. iii  y  f  x 

41. iii  y  f  x 

42. iii  y  f  x 

43. iii  y  f  x 

44. iv  y  log f  x 

45. iv  y  log f  x 

46. iv  y  log f  x 

47. iv  y  log f  x 

48. Exercise 1A; 9, 10, 11a, 12
Exercise 1B; 2bd, 9egh, 11ace, 13af, 14abf, 30, 32e, 34