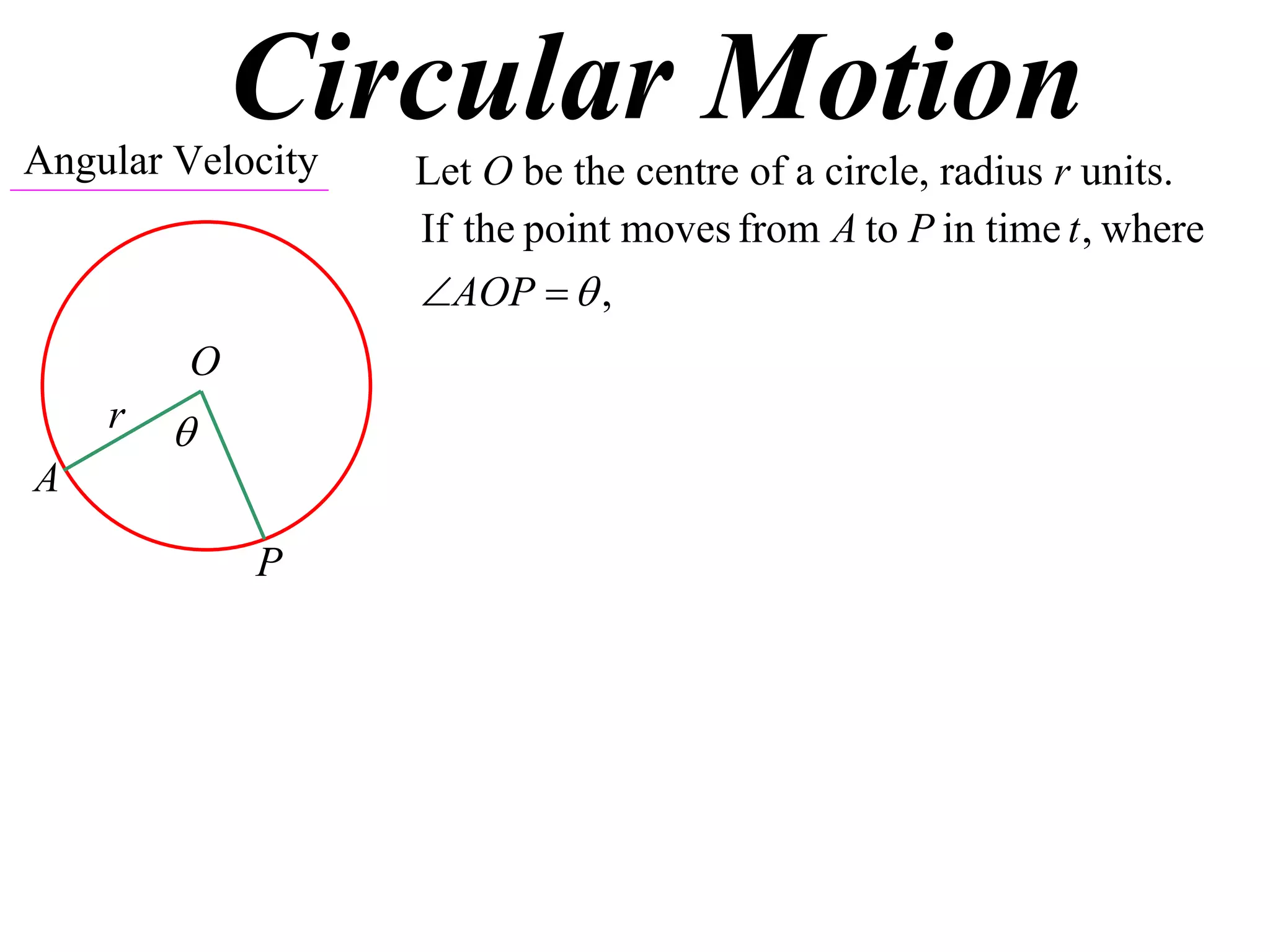
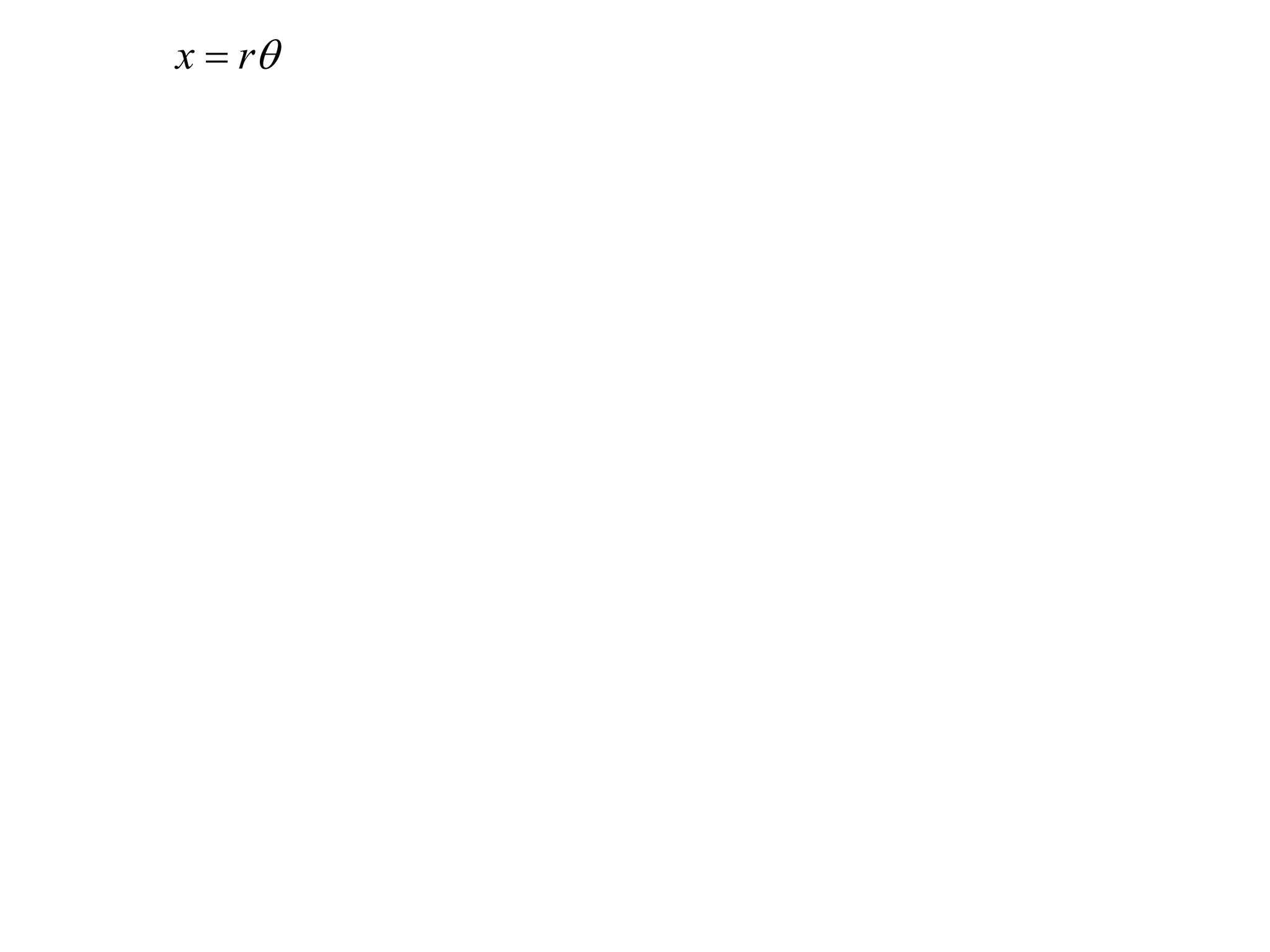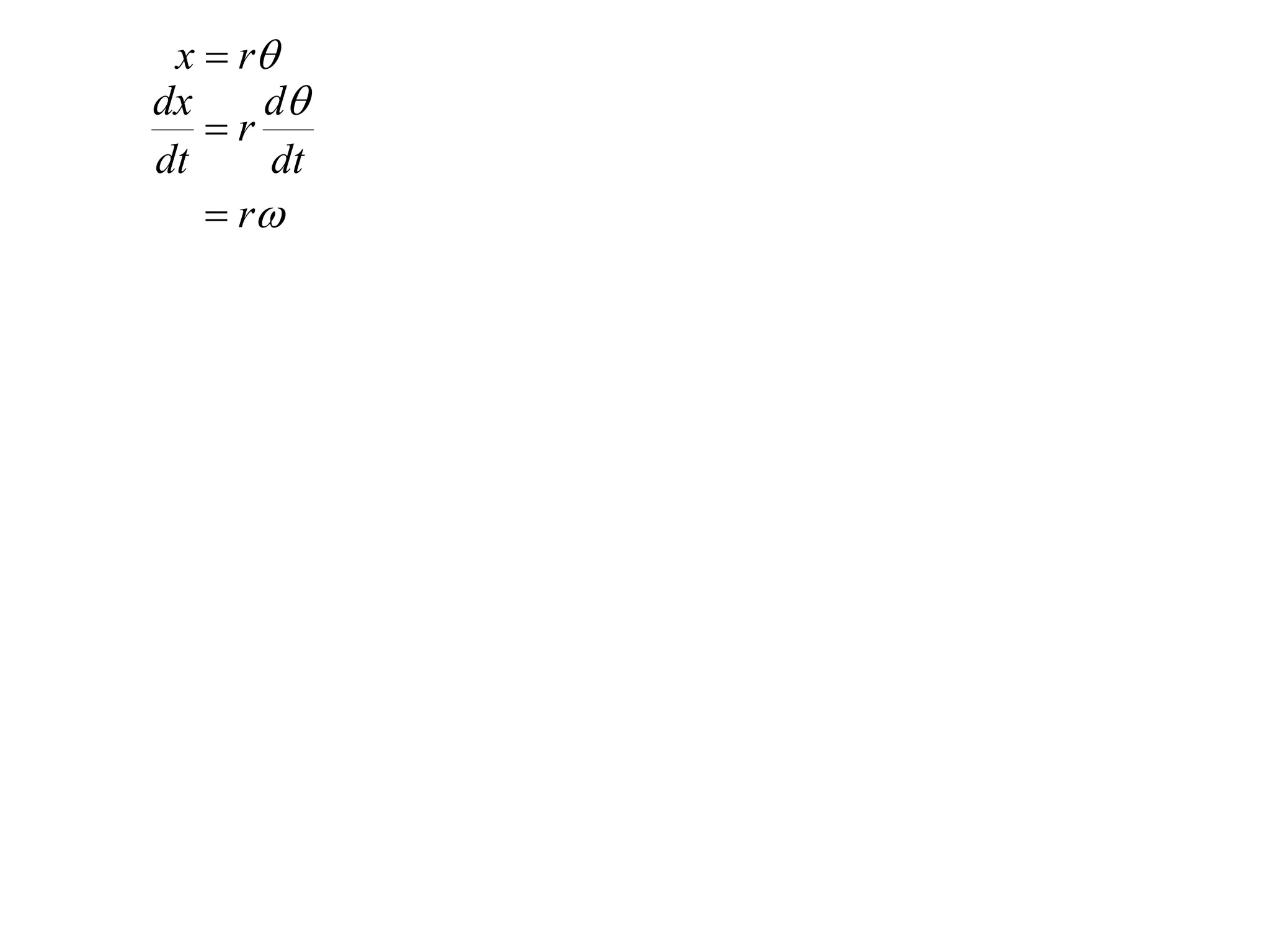The document defines angular velocity as the rate of change of the angle swept out by a point moving along a circular path with respect to time. It shows that the linear or tangential velocity of the point is equal to the product of its angular velocity and radius. The period of motion is defined as the time taken for one complete revolution, which is calculated by dividing 2π by the angular velocity. An example calculates the angular velocity and tangential velocity of a satellite in circular orbit.

1. Circular Motion

2. Circular Motion
Angular Velocity

3. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
O
r

4. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
If the point moves from A to P in time t , where
AOP   ,
O
r 
A
P

5. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
If the point moves from A to P in time t , where
AOP   , then the angular velocity,  , of the
O point is defined as the rate of change of  with
r  respect to time.
A measured in radians/second
P

6. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
If the point moves from A to P in time t , where
AOP   , then the angular velocity,  , of the
O point is defined as the rate of change of  with
r  respect to time.
A measured in radians/second
d
P 
dt
 

7. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
If the point moves from A to P in time t , where
AOP   , then the angular velocity,  , of the
O point is defined as the rate of change of  with
r  respect to time.
A measured in radians/second
d
P 
dt
 
Linear Velocity (Tangential Velocity)

8. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
If the point moves from A to P in time t , where
AOP   , then the angular velocity,  , of the
O point is defined as the rate of change of  with
r  respect to time.
A measured in radians/second
d
P 
dt
 
Linear Velocity (Tangential Velocity)
The linear velocity, v, of the point at every position on its path is
tangential to the circle.

9. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
If the point moves from A to P in time t , where
AOP   , then the angular velocity,  , of the
O point is defined as the rate of change of  with
r  respect to time.
A measured in radians/second
v
d
P 
dt
 
Linear Velocity (Tangential Velocity)
The linear velocity, v, of the point at every position on its path is
tangential to the circle.

10. Circular Motion
Angular Velocity Let O be the centre of a circle, radius r units.
If the point moves from A to P in time t , where
AOP   , then the angular velocity,  , of the
O point is defined as the rate of change of  with
r  respect to time.
A measured in radians/second
v
d
P 
dt
 
Linear Velocity (Tangential Velocity)
The linear velocity, v, of the point at every position on its path is
tangential to the circle.
Let arc AP = x

11. x  r

12. x  r
dx d
r
dt dt
 r

13. x  r v  r
dx d
r OR
dt dt
 r v  r

14. x  r v  r
dx d
r OR
dt dt
 r v  r
Period

15. x  r v  r
dx d
r OR
dt dt
 r v  r
Period
2
T (time taken for one revolution)


16. x  r v  r
dx d
r OR
dt dt
 r v  r
Period
2
T (time taken for one revolution)

e.g. A satellite moves in a circular orbit of 20 rev/day
a) Describe  in rad/s

17. x  r v  r
dx d
r OR
dt dt
 r v  r
Period
2
T (time taken for one revolution)

e.g. A satellite moves in a circular orbit of 20 rev/day
a) Describe  in rad/s
  20  2 rad/day

18. x  r v  r
dx d
r OR
dt dt
 r v  r
Period
2
T (time taken for one revolution)

e.g. A satellite moves in a circular orbit of 20 rev/day
a) Describe  in rad/s
  20  2 rad/day
20  2
 rad/s
24  60  60

 rad/s
2160

19. b) Find the satellite' s tangential velocity, given that its radius is 9000km,
in km/h

20. b) Find the satellite' s tangential velocity, given that its radius is 9000km,
in km/h
v  r

 9000  km/s
2160

21. b) Find the satellite' s tangential velocity, given that its radius is 9000km,
in km/h
v  r

 9000  km/s
2160

 9000   60  60km/h
2160
 15000km/h

22. b) Find the satellite' s tangential velocity, given that its radius is 9000km,
in km/h
v  r

 9000  km/s
2160

 9000   60  60km/h
2160
 15000km/h
Exercise 9A; odd