More Related Content
What's hot
What's hot (20)
Similar to Conservación del momento angular
Similar to Conservación del momento angular (20)
More from jolopezpla
More from jolopezpla (20)
Recently uploaded
Recently uploaded (20)
Conservación del momento angular
- 1. -CONSERVACIÓN DEL MOMENTO ANGULAR Naturaleza vectorial de la rotación 1. (a) Si dos vectores son paralelos, su producto vectorial es cero. (b) Cuando un disco gira alrededor de su eje de simetría, el vector ω está dirigido a lo largo de su eje. (c) El momento ejercido por una fuerza es siempre perpendicular a la fuerza. Los tres son verdaderos. En (a) por ser sen0=0 ; En (b) por ser el vector ω perpendicular al plano de la rotación y en (c) por ser el momento el producto vectorial de la fuerza por la distancia al eje de rotación. 2. Dos vectores A y B poseen el mismo módulo. Su producto vectorial alcanza su módulo máximo cuando A y B son: a) Paralelas b) Iguales c) Perpendiculares d) Antiparalelas e) Forman entre sí un ángulo de 45º. La respuesta correcta es la c. El producto vectorial será máximo si sen90=1. 3. Se aplica una fuerza de valor F horizontalmente en el sentido negativo de las x al borde de un disco de radio R, como se muestra en la figura. Escribir F y r en función de los vectores unitarios i, j y k y calcular el momento producido por la fuerza respecto al origen situado en el centro del disco. 𝑭 ⃗ ⃗ = − 𝑭 ∗ 𝒊 𝒓 ⃗ = 𝑹 ∗ 𝒋 𝑴 ⃗⃗⃗ = 𝒓 ⃗ 𝒙𝑭 ⃗ ⃗ = | 𝒊 𝒋 𝒌 𝟎 𝑹 𝟎 −𝑭 𝟎 𝟎 | = 𝑹 ∗ 𝑭 ∗ 𝒌 ⃗ ⃗ 4. Calcular el momento respecto al origen debido a la fuerza F=-mgj que actúa sobre una partícula situada en r=xi+yj, y demostrar que este momento es independiente de la coordenada y. 𝑴 ⃗⃗⃗ = 𝒓 ⃗ 𝒙𝑭 ⃗ ⃗ = | 𝒊 𝒋 𝒌 𝒙 𝒚 𝟎 𝟎 −𝒎 ∗ 𝒈 𝟎 | = (−𝒙 ∗ 𝒎 ∗ 𝒈) ∗ 𝒌 ⃗ ⃗ Como se ve el resultado no depende de y. 5. Hallar AXB en el caso de a) A=4 i y B=6 i+6 j.
- 2. b) A=4 i y B = 6 i + 6 k c) A= 2 i +3 j y B= -3 i+ 2 j a) 𝑨 ⃗⃗ 𝒙𝑩 ⃗⃗ = | 𝒊 𝒋 𝒌 𝟒 𝟎 𝟎 𝟔 𝟔 𝟎 | = 𝟒 ∗ 𝟔 𝒌 ⃗ ⃗ = 𝟐𝟒 𝒌 ⃗ ⃗ b) 𝑨 ⃗⃗ 𝒙𝑩 ⃗⃗ = | 𝒊 𝒋 𝒌 𝟒 𝟎 𝟎 𝟔 𝟎 𝟔 | = − 𝟐𝟒 𝒋 c) 𝑨 ⃗⃗ 𝒙𝑩 ⃗⃗ = | 𝒊 𝒋 𝒌 𝟐 𝟑 𝟎 −𝟑 𝟐 𝟎 | = (𝟐 ∗ 𝟐 + 𝟑 ∗ 𝟑)𝒌 ⃗ ⃗ = −𝟏𝟑 𝒌 ⃗ ⃗ 6. ¿En qué condiciones es el módulo de AXB igual a A·B? 𝑨 ∗ 𝑩 ∗ 𝒔𝒆𝒏𝝋 = 𝑨 ∗ 𝑩 ∗ 𝒄𝒐𝒔𝝋 Por tanto, la condición es 𝒔𝒆𝒏𝝋 = 𝒄𝒐𝒔𝝋 𝝋 = 𝟒𝟓º o 135 º. 7. Una partícula se mueve en un círculo de radio r con una velocidad angular ω. a) Demostrar que su velocidad es v=ωXr. b) Demostrar que su aceleración centrípeta es ac=ωX(ωXr). a) El círculo de movimiento está en el plano x, y. 𝝎 ⃗⃗⃗ = 𝝎 𝒌 ⃗ ⃗ 𝒓 ⃗ = 𝒙 𝒊 + 𝒚𝒋 |𝝎 ⃗⃗⃗ 𝑿𝒓 ⃗ | = 𝝎 ∗ 𝑹 ∗ 𝒔𝒊𝒏𝟗𝟎 = 𝝎 ∗ 𝑹 El módulo es constante. 𝝎 ⃗⃗⃗ 𝑿𝒓 ⃗ = | 𝒊 𝒋 𝒌 𝟎 𝟎 𝝎 𝒙 𝒚 𝟎 | = −𝝎 ∗ 𝒚 𝒊 + 𝝎 ∗ 𝒙 𝒋 Si consideramos el momento inicial como el punto (R,0): 𝝎 ⃗⃗⃗ 𝑿𝒓 ⃗ = 𝝎 ∗ 𝑹 ∗ 𝒋 Si miramos el momento donde la posición es (0,R): 𝝎 ⃗⃗⃗ 𝑿𝒓 ⃗ = − 𝝎 ∗ 𝑹 ∗ 𝒊
- 3. En un punto cualquiera: b) 𝒂 ⃗ ⃗ = 𝒅𝒗 ⃗ ⃗ 𝒅𝒕 = 𝒅𝝎 ⃗⃗⃗ 𝒅𝒓 𝑿𝒓 ⃗ + 𝝎 ⃗⃗⃗ 𝑿 𝒅𝒓 ⃗ 𝒅𝒕 = 𝒅𝝎 ⃗⃗⃗ 𝒅𝒓 𝑿𝒓 ⃗ + 𝝎 ⃗⃗⃗ 𝑿𝒗 ⃗ ⃗ = 𝒂𝒕 ⃗⃗⃗⃗ + 𝝎 ⃗⃗⃗ 𝑿(𝒘 ⃗⃗⃗ 𝑿𝒓 ⃗ ) = 𝒂𝒕 ⃗⃗⃗⃗ + 𝒂𝒄 ⃗⃗⃗⃗ 8. Si A= 4 i , Bz=0, |𝑩| = 𝟓 y AXB= 12 k, determinar B. B estará en el plano x,y. 𝟏𝟐 = 𝟒 ∗ 𝟓 ∗ 𝒔𝒆𝒏𝜶 ; 𝒔𝒆𝒏𝜶 = 𝟎, 𝟔 ; 𝜶 = 𝟑𝟔,𝟗º 𝑩𝒙 = 𝑩 ∗ 𝒄𝒐𝒔𝟑𝟔,𝟗 = 𝟒 ; 𝑩𝒚 = 𝟓 ∗ 𝒔𝒆𝒏𝟑𝟔,𝟗 = 𝟑 𝑩 ⃗⃗ = 𝟒 𝒊 + 𝟑 𝒋 9. Si A= 3 j, AXB= 9 i y A·B=12, determinar B. B estará en el plano y,z . 𝟑 ∗ 𝑩 ∗ 𝒔𝒆𝒏𝜶 = 𝟗 𝟑 ∗ 𝑩 ∗ 𝒄𝒐𝒔𝜶 = 𝟏𝟐 𝒕𝒂𝒏𝜶 = 𝟗 𝟏𝟐 ; 𝜶 = 𝒂𝒕𝒂𝒏( 𝟗 𝟏𝟐 ) = 𝟑𝟔,𝟗𝒐 𝑩 = 𝟑 𝒔𝒆𝒏𝜶 = 𝟓 𝑩𝒛 = 𝑩 ∗ 𝒔𝒆𝒏(𝟑𝟔,𝟗) = 𝟓 ∗ 𝒔𝒆𝒏(𝟑𝟔,𝟗) = 𝟑 𝑩𝒚 = 𝟓 ∗ 𝒄𝒐𝒔(𝟑𝟔,𝟗) = 𝟒 𝑩 ⃗⃗ = 𝟒 𝒋 + 𝟑 𝒌 ⃗ ⃗ Momento angular 10. ¿Cuál es el ángulo que forman el momento lineal p de una partícula y su momento angular? 𝑳 ⃗ ⃗ = 𝒓 ⃗ 𝒙𝒑 ⃗ ⃗ Por tanto, L será perpendicular a r y a p. 11. Una partícula de masa m se mueve a velocidad v a lo largo de una línea que pasa a través del punto P. ¿Cuál es el momento angular de la partícula respecto a dicho punto P? a) mv. b) Cero. c) Cambia de signo cuando la partícula pasa a través del punto P. d) Depende de la distancia del punto P al origen de coordenadas.
- 4. El ángulo entre r y p será de 0 o de 180º. Como sen de estos ángulos es 0, el vector L será 0. Respuesta b. 12. Una partícula describe una trayectoria circular. a) Si su momento lineal p se duplica, ¿Cómo se modifica su momento angular? b) Si el radio del círculo se duplica, pero su velocidad no varía, ¿Cómo se modifica el momento angular de la partícula? a) El momento angular se duplica. b) El momento angular se duplica. 13. Una partícula se mueve a lo largo de una línea recta a velocidad constante. ¿Cómo varía con el tiempo su momento angular respecto a cualquier punto? 𝑳 ⃗ ⃗ = 𝒓 ⃗ 𝒙𝒑 ⃗ ⃗ 𝒅𝑳 ⃗ ⃗ 𝒅𝒕 = 𝒅𝒓 ⃗ 𝒅𝒕 𝒙 𝒑 ⃗ ⃗ + 𝒓 ⃗ 𝒙 𝒅𝒑 ⃗ ⃗ 𝒅𝒕 = 𝒓 ⃗ 𝒙 (𝒎 ∗ 𝒂 ⃗ ⃗ ) = 𝒓 ⃗ 𝒙 𝑭 ⃗ ⃗ = 𝟎 ;𝒑𝒐𝒓 𝒔𝒆𝒓 𝑭 𝒄𝒆𝒓𝒐. 14. Una partícula que se mueve a velocidad constante, tiene un momento angular nulo respecto a un determinado punto. Demostrar que la partícula ha pasado a través de dicho punto o pasará por él. 𝑳 ⃗ ⃗ = 𝒓 ⃗ 𝒙𝒑 ⃗ ⃗ = 𝟎 Por tanto, el ángulo entre r y p ha de ser 0 0 180. Esto quiere decir que o bien ha pasado por el punto considerado (ángulo 0º) o bien pasará por él (ángulo 180º). 15. Una partícula de masa 2 kg se mueve con velocidad constante de 3,5 m/s describiendo una circunferencia de 4 m de radio. a) ¿Cuál es su momento angular respecto al centro de la circunferencia? b) ¿Cuál es su momento de inercia respecto a un eje que pasa por el centro de la circunferencia y es perpendicular al plano del movimiento? c) ¿Cuál es la velocidad angular de la partícula? a) 𝑳 ⃗ ⃗ = 𝒓 ⃗ 𝒙𝒑 ⃗ ⃗ = 𝟒 ∗ 𝟐 ∗ 𝟑,𝟓 ∗ 𝒔𝒆𝒏𝟗𝟎 ∗ 𝒌 ⃗ ⃗ = 𝟐𝟖 𝒌 ⃗ ⃗ b) 𝑰 = 𝒎 ∗ 𝒓𝟐 = 𝟐 ∗ 𝟒𝟐 = 𝟑𝟐 𝒌𝒈 ∗ 𝒎𝟐 c) 𝝎 = 𝒗 𝒓 = 𝟑,𝟓 𝟒 = 𝟎, 𝟖𝟕𝟓 𝒓𝒂𝒅/𝒔 16. Un cuerpo de 2 kg se mueve a velocidad constante de 4,5 m/s a lo largo de una línea recta. a) ¿Cuál es el módulo de su momento angular respecto a un punto situado a 6 m de la línea? b) Describir cualitativamente cómo varia en el tiempo su velocidad angular respecto a dicho punto. a) 𝑳 = 𝟔 ∗ 𝟐 ∗ 𝟒, 𝟓 = 𝟓𝟒 𝒌𝒈 𝒎/𝒔 b) 𝑳 = 𝒓 ∗ 𝒎 ∗ 𝒗 = 𝒓 ∗ 𝒎 ∗ 𝝎 ∗ 𝒓 = 𝒎 ∗ 𝝎 ∗ 𝒓𝟐 La velocidad angular aumenta al acercarse al punto y disminuye al alejarse.
- 5. 17. Una partícula se mueve con velocidad constante v a lo largo de una línea que está a una distancia b del origen O (figura). Sea dA el área barrida por el vector posición (desde O a la partícula) en el tiempo dt. Demostrar que dA/dt es constante en el tiempo e igual a ½ L/m, en donde L es el momento angular de la partícula respecto al origen. 𝑨𝟏 = 𝟏 𝟐 ∗ 𝒃 ∗ 𝒓𝟏 ∗ 𝒄𝒐𝒔𝜽𝟏 = 𝟏 𝟐 ∗ 𝒃 ∗ 𝒙𝟏; donde 𝜽𝟏es el ángulo entre 𝒓𝟏 y v. El área barrida es. 𝑨 = 𝑨𝟏 + 𝒅𝑨 = 𝟏 𝟐 ∗ 𝒃 ∗ (𝒙𝟏 + 𝒅𝒙) = 𝟏 𝟐 ∗ 𝒃 ∗ (𝒙𝟏 + 𝒗 ∗ 𝒅𝒕) Derivando: 𝒅𝑨 𝒅𝒕 = 𝟏 𝟐 ∗ 𝒃 ∗ 𝒗 ; que es constante. Por otro lado: 𝒃 = 𝒓 ∗ 𝒔𝒆𝒏𝜽 𝒅𝑨 𝒅𝒕 = 𝟏 𝟐 ∗ 𝒓 ∗ 𝒔𝒆𝒏𝜽 ∗ 𝒗 = 𝟏 𝟐∗𝒎 ∗ 𝒓 ∗ 𝒑 ∗ 𝒔𝒆𝒏𝜽 = 𝑳 𝟐∗𝒎 18. Una moneda de 15 g y diámetro 1,5 cm gira a 10 rev/s alrededor de un diámetro vertical sobre un punto fijo de una mesa. a) ¿Cuál es el momento angular respecto de su centro de masas? b) ¿Cuál es el momento angular respecto a un punto de la mesa situado a 10 cm de la moneda? c) Si la moneda gira de igual modo, pero su centro de masas se traslada en línea recta sobre la mesa con velocidad de 5 cm/s, ¿Cuál es el momento angular de la moneda alrededor de un punto sobre la línea de movimiento? d) ¿Cuál es el momento angular de la moneda respecto a un punto situado a 10 cm de la línea de movimiento? (Existen dos respuestas a esta cuestión. Explicar por qué y expresar ambas). a) 𝑳 = 𝑰 ∗ 𝝎 Para la moneda (cilindro de longitud 0): 𝑰 = 𝟏 𝟒 ∗ 𝑴 ∗ 𝑹𝟐 𝑳 = 𝟏 𝟒 ∗ 𝟎, 𝟎𝟏𝟓 ∗ 𝟎, 𝟎𝟎𝟕𝟓𝟐 ∗ 𝟏𝟎𝒓𝒆𝒗 𝒔 ∗ 𝟐∗𝝅 𝒓𝒂𝒅 𝟏 𝒓𝒆𝒗 = 𝟏, 𝟑𝟑 𝟏𝟎−𝟓 𝑲𝒈 𝒎𝟐 𝒔 b) El momento angular de un objeto se puede considerar formado por dos partes, el momento angular respecto de su centro de masas o de spin y el momento angular asociado con el movimiento de su centro de masas, llamado momento angular orbital. 𝑳 = 𝑳𝒐𝒓𝒃𝒊𝒕𝒂 + 𝑳𝒔𝒑𝒊𝒏 = 𝒓𝒄𝒎𝒙 𝑴 ∗ 𝒗𝒄𝒎 + 𝑳𝒔𝒑𝒊𝒏 El centro de masas no se traslada, por tanto: 𝑳 = 𝑳𝒔𝒑𝒊𝒏 = 𝟏,𝟑𝟑 𝟏𝟎−𝟓 𝑲𝒈 𝒎𝟐 𝒔 c) Sobre la línea de movimiento el momento angular es el mismo que en el caso anterior. d) En este caso si existirá momento angular orbital.
- 6. 𝑳𝒐𝒓𝒃𝒊𝒕𝒂 = 𝟎,𝟎𝟏 ∗ 𝟎,𝟎𝟏𝟓 ∗ 𝟎,𝟎𝟓 = 𝟕,𝟓 𝟏𝟎−𝟓 𝑲𝒈 𝒎𝟐 𝒔 El ángulo entre r y la velocidad del centro de masas puede ser 0 o 180, por tanto, el signo puede ser positivo o negativo. Las dos soluciones son: 𝑳 = 𝟕,𝟓 𝟏𝟎−𝟓 + 𝟏, 𝟑𝟑 𝟏𝟎−𝟓 = 𝟖,𝟖𝟑 𝟏𝟎−𝟓 𝑲𝒈 𝒎𝟐 𝒔 𝑳 = 𝟕,𝟓 𝟏𝟎−𝟓 − 𝟏, 𝟑𝟑 𝟏𝟎−𝟓 = 𝟔,𝟏𝟕 𝟏𝟎−𝟓 𝑲𝒈 𝒎𝟐 𝒔 19. Dos partículas de masa m1 y m2 están localizadas en las posiciones r1 y r2 respecto al mismo origen O como indica la figura. Estas partículas ejercen fuerzas iguales y opuestas una sobre otra. Calcular el momento resultante ejercido por estas fuerzas internas alrededor del origen O y demostrar que es nulo si las fuerzas F1 y F2 están dirigidas a lo largo de la línea que une ambas partículas. 𝝉 = 𝒓𝟏𝒙𝑭𝟏 + 𝒓𝟐𝒙𝑭𝟐 = (𝒓𝟏 − 𝒓𝟐)𝒙𝑭𝟏 ; por ser 𝑭𝟏 = −𝑭𝟐 El ángulo entre r1 y r2 es 0 o 180, 𝝉 = 𝟎. Momento de una fuerza y momento angular 20. Verdadero o falso: a) La variación respecto al tiempo del momento angular de un sistema es siempre paralela al momento externo resultante. b) Si el momento resultante sobre un cuerpo es nulo, el momento angular debe ser cero. a) Verdadero. 𝝉 = 𝒅𝑳 𝒅𝒕 b) Falso, si el momento es nulo, L es constante. 21. Una partícula de 1,8 kg se mueve en una circunferencia de radio 3,4 m. La magnitud de su momento angular relativa al centro del circulo depende del tiempo según la expresión L=(4 N·m) t. a) Determinar la magnitud del momento que actúa sobre la partícula. b) Determinar la velocidad angular de la partícula en función del tiempo. a) 𝝉 = 𝒅𝑳 𝒅𝒕 = 𝟒 𝑵 𝒎 b) 𝝉 = 𝑰 ∗ 𝜶 ; 𝜶 = 𝝉 𝑰 = 𝟒 𝟏,𝟖∗𝟑,𝟒𝟐 = 𝟎, 𝟏𝟗𝟐 𝒓𝒂𝒅/𝒔𝟐 𝝎 = 𝜶 ∗ 𝒕 = 𝟎,𝟏𝟗𝟐 ∗ 𝒕
- 7. 22. Un cilindro uniforme de masa 90 kg y radio 0,4 m está dispuesto de modo que gira sin rozamiento alrededor de su eje de simetría, gracias a una correa de transmisión que se arrolla sobre su perímetro y ejerce un momento constante. En el tiempo t=0 su velocidad angular es cero. En el tiempo t=25 s su velocidad angular es de 500 rev/min. a) ¿Cuál es su momento angular en t= 25 s? b) ¿Cómo se incrementa el momento angular en cada unidad de tiempo? c) ¿Qué momento externo actúa sobre el cilindro? d) ¿Cuál es la magnitud de la fuerza que actúa sobre la periferia del cilindro? a) 𝑳 = 𝑰 ∗ 𝝎 = 𝟏 𝟐 ∗ 𝟗𝟎 ∗ 𝟎, 𝟒𝟐 ∗ (𝟓𝟎𝟎 𝒓𝒆𝒗 𝒎𝒊𝒏 ∗ 𝟏 𝒎𝒊𝒏 𝟔𝟎 𝒔 ∗ 𝟐 𝝅 𝒓𝒂𝒅 𝟏 𝒓𝒆𝒗 ) = 𝟑𝟕𝟕 𝒌𝒈 ∗ 𝒎𝟐 /𝒔 b) 𝒅𝑳 𝒅𝒕 = 𝟑𝟕𝟕 𝟐𝟓 = 𝟏𝟓,𝟏 𝒌𝒈 ∗ 𝒎𝟐 /𝒔𝟐 c) 𝝉 = 𝒅𝑳 𝒅𝒕 = 𝟏𝟓,𝟏 𝒌𝒈 ∗ 𝒎𝟐 /𝒔𝟐 d) 𝝉 = 𝑭 ∗ 𝒓 ∗ 𝒔𝒊𝒏 𝟗𝟎 ;𝑭 = 𝝉 𝒓 = 𝟏𝟓,𝟏 𝟎,𝟒 = 𝟑𝟕,𝟕 𝑵 23. En la figura el plano inclinado carece de rozamiento y la cuerda pasa a través del centro de masas de cada bloque. La polea tiene un momento de inercia I y un radio R. a) Determinar el momento resultante que actúa sobre el sistema (las dos masas, la cuerda y la polea) respecto al centro de la polea. b) Expresar el momento angular total del sistema respecto al centro de la polea cuando las masas se mueven a velocidad v. c) Determinar la aceleración de las masas a partir de los resultados de las partes (a) y (b), igualando el momento resultante con la derivada respecto al tiempo del momento angular del sistema. a) El momento del sistema será el de la polea. 𝝉 = (𝒎𝟐 ∗ 𝒔𝒆𝒏𝜽 − 𝒎𝟏) ∗ 𝒈 ∗ 𝑹 b) 𝑳 = 𝑰 ∗ 𝝎 + 𝒎𝟏 ∗ 𝒗 ∗ 𝑹 + 𝒎𝟐 ∗ 𝒗 ∗ 𝑹 = (𝑰 ∗ 𝒗 𝑹 + 𝒎𝟏 ∗ 𝒗 ∗ 𝑹 + 𝒎𝟐 ∗ 𝒗 ∗ 𝑹) 𝑳 = 𝑹 ∗ 𝒗 ∗ ( 𝑰 𝑹𝟐 + 𝒎𝟏 + 𝒎𝟐) c) 𝝉 = 𝒅𝑳 𝒅𝒕 = 𝑹 ∗ 𝒂 ∗ ( 𝑰 𝑹𝟐 + 𝒎𝟏 + 𝒎𝟐) = (𝒎𝟐 ∗ 𝒔𝒆𝒏𝜽 − 𝒎𝟏) ∗ 𝒈 ∗ 𝑹 𝒂 = (𝒎𝟐∗𝒔𝒆𝒏𝜽−𝒎𝟏)∗𝒈 ( 𝑰 𝑹𝟐+𝒎𝟏+𝒎𝟐) 24. Desde una elevada cabina de un club de baile un empleado hace descender un altavoz de 2 kg mediante una polea formada por un disco de 0,6 kg y radio 8 cm. El cable del altavoz sube verticalmente, rodea la polea y continúa horizontalmente sobre la mesa hasta conectar con el amplificador de masa 4 kg. El empleado se dispone a conectar en el otro extremo un segundo altavoz. Sin embargo, como la mesa prácticamente no tiene rozamiento, todo el sistema comienza a deslizar. a) ¿Cuál es el momento resultante respecto al centro de la polea?
- 8. b) ¿Cuál es el momento angular total del sistema 3,5 s después de iniciarse el movimiento? c) ¿Cuál es el momento angular de la polea en ese momento? d) ¿Cuál es la relación que existe entre el momento angular de cada pieza y el momento angular de la polea? a) Sea 1 el amplificador, 2 el altavoz y 3 la polea. La fuerza causante de momento es únicamente el peso de 2: 𝝉 = 𝒎𝟐 ∗ 𝒈 ∗ 𝑹 = 𝟐 ∗ 𝟗,𝟖 ∗ 𝟎, 𝟎𝟖 = 𝟏, 𝟓𝟔𝟖 𝑵 𝒎 b) 𝑻𝟏 = 𝒎𝟏 ∗ 𝒂 𝒎𝟐 ∗ 𝒈 − 𝑻𝟐 = 𝒎𝟐 ∗ 𝒂 (𝑻𝟐 − 𝑻𝟏) ∗ 𝑹 = 𝑰 ∗ 𝜶 = 𝟏 𝟐 ∗ 𝒎𝟑 ∗ 𝑹𝟐 ∗ 𝒂 𝑹 De estas ecuaciones obtenemos a: 𝒂 = 𝒎𝟐∗𝒈 𝟏 𝟐 ∗𝒎𝟑+𝒎𝟏+𝒎𝟐 = 𝟐∗𝟗,𝟖 𝟏 𝟐 ∗𝟎,𝟔+𝟒+𝟐 = 𝟑, 𝟏 𝒎 𝒔𝟐 𝑷𝒐𝒓 𝒕𝒂𝒏𝒕𝒐: 𝐯 = 𝐚 ∗ 𝐭 = 𝟑, 𝟏 ∗ 𝟑,𝟓 = 𝟏𝟎,𝟗 𝐦/𝐬 𝑳 = 𝑰 ∗ 𝒘 + 𝒎𝟏 ∗ 𝒗 ∗ 𝑹 + 𝒎𝟐 ∗ 𝒗 ∗ 𝑹 = 𝑹 ∗ 𝒗 ∗ ( 𝟏 𝟐 ∗ 𝒎𝟑 + 𝒎𝟏 + 𝒎𝟐) 𝑳 = 𝟎,𝟎𝟖 ∗ 𝟏𝟎.𝟗 ∗ ( 𝟏 𝟐 ∗ 𝟎, 𝟔 + 𝟒 + 𝟐) = 𝟓,𝟓 𝒌𝒈 𝒎𝟐 /𝒔 c) 𝑳(𝒑𝒐𝒍𝒆𝒂) = 𝑰 ∗ 𝒘 = 𝟏 𝟐 ∗ 𝟎,𝟔 ∗ 𝟏𝟎,𝟗 ∗ 𝟎, 𝟎𝟖 = 𝟎,𝟐𝟔𝒌𝒈 𝒎𝟐 /𝒔 d) 𝑳𝟏 𝑳(𝒑𝒐𝒍𝒆𝒂) = 𝒎𝟏 𝟏 𝟐 ∗𝒎𝟑 = 𝟐∗𝟒 𝟎,𝟔 = 𝟏𝟑, 𝟑 𝑳𝟐 𝑳(𝒑𝒐𝒍𝒆𝒂) = 𝒎𝟐 𝟏 𝟐 ∗𝒎𝟑 = 𝟐∗𝟐 𝟎,𝟔 = 𝟔,𝟕 25. Repetir el problema 24 para el caso en que el coeficiente de rozamiento entre la mesa y el amplificador sea 0,25. a) Únicamente cambia el hecho de aparecer una fuerza de fricción sobre la masa 1. El momento total ahora será: 𝝉 = 𝒎𝟐 ∗ 𝒈 ∗ 𝑹 − 𝝁 ∗ 𝒎𝟏 ∗ 𝒈 ∗ 𝑹 = (𝟐 − 𝟎,𝟐𝟓 ∗ 𝟒) ∗ 𝟗, 𝟖 ∗ 𝟎,𝟎𝟖 = 𝟎,𝟕𝟖𝟒 𝑵 𝒎 b) 𝑻𝟏 − 𝝁 ∗ 𝒎𝟏 ∗ 𝒈 = 𝒎𝟏 ∗ 𝒂 𝒎𝟐 ∗ 𝒈 − 𝑻𝟐 = 𝒎𝟐 ∗ 𝒂 (𝑻𝟐 − 𝑻𝟏) ∗ 𝑹 = 𝑰 ∗ 𝜶 = 𝟏 𝟐 ∗ 𝒎𝟑 ∗ 𝑹𝟐 ∗ 𝒂 𝑹 Obtenemos a: 𝒂 = 𝒎𝟐∗𝒈+𝝁∗𝒎𝟏∗𝒈 𝟏 𝟐 ∗𝒎𝟑+𝒎𝟏−𝒎𝟐 = 𝟗,𝟖∗(𝟐−𝟎,𝟐𝟓∗𝟒) 𝟏 𝟐 ∗𝟎,𝟔+𝟒+𝟐 = 𝟏, 𝟔 𝒎 𝒔𝟐 𝐯 = 𝐚 ∗ 𝐭 = 𝟏,𝟔 ∗ 𝟑, 𝟓 = 𝟓,𝟒𝟔 𝐦/𝐬
- 9. 𝑳 = 𝑰 ∗ 𝒘 + 𝒎𝟏 ∗ 𝒗 ∗ 𝑹 + 𝒎𝟐 ∗ 𝒗 ∗ 𝑹 = 𝑹 ∗ 𝒗 ∗ ( 𝟏 𝟐 ∗ 𝒎𝟑 + 𝒎𝟏 + 𝒎𝟐) 𝑳 = 𝟎,𝟎𝟖 ∗ 𝟓,𝟒𝟔 ∗ ( 𝟏 𝟐 ∗ 𝟎, 𝟔 + 𝟒 + 𝟐) = 𝟐,𝟕𝟓 𝒌𝒈 𝒎𝟐 /𝒔 c) 𝑳(𝒑𝒐𝒍𝒆𝒂) = 𝑰 ∗ 𝒘 = 𝟏 𝟐 ∗ 𝟎,𝟔 ∗ 𝟓, 𝟒𝟔 ∗ 𝟎, 𝟎𝟖 = 𝟎,𝟏𝟑𝟏 𝒌𝒈 𝒎𝟐 /𝒔 d) 𝑳𝟏 𝑳(𝒑𝒐𝒍𝒆𝒂) = 𝒎𝟏 𝟏 𝟐 ∗𝒎𝟑 = 𝟐∗𝟒 𝟎,𝟔 = 𝟏𝟑, 𝟑 𝑳𝟐 𝑳(𝒑𝒐𝒍𝒆𝒂) = 𝒎𝟐 𝟏 𝟐 ∗𝒎𝟑 = 𝟐∗𝟐 𝟎,𝟔 = 𝟔,𝟕 26. La figura muestra la parte trasera de un vehículo espacial que gira alrededor de su eje longitudinal a 6 rev/min. Los ocupantes desean detener esta rotación. Para ello disponen de pequeñas toberas montadas tangencialmente a una distancia R= 3 m del eje, como se indica en la figura. Cada una de ellas lanza un chorro de 10 g/s de gas a una velocidad de 800 m/s. ¿Durante cuánto tiempo deben estar funcionando estas toberas para detener la rotación? La inercia rotacional del vehículo alrededor de su eje (supuesta constante) es de 4000 kg m2 . 𝝉 = ∆𝑳 ∆𝒕 = 𝑰∗∆𝝎 ∆𝒕 𝝉 = 𝟐 ∗ 𝑭 ∗ 𝑹 = 𝟐 ∗ ∆𝒑 ∆𝒕 ∗ 𝑹 = 𝟐 ∗ ∆𝒎 ∆𝒕′ ∗ 𝒗 ∗ 𝑹 𝟐 ∗ ∆𝒎 ∆𝒕′ ∗ 𝒗 ∗ 𝑹 = 𝑰∗∆𝝎 ∆𝒕 ∆𝒕 = 𝑰∗∆𝝎 𝒗∗𝑹∗𝟐∗ ∆𝒎 ∆𝒕′ = 𝟒𝟎𝟎𝟎 𝒌𝒈 𝒎𝟐∗( 𝟔𝒓𝒆𝒗 𝒎𝒊𝒏 ∗ 𝟐∗𝝅 𝒓𝒂𝒅 𝟏 𝒓𝒆𝒗 ∗ 𝟏 𝒎𝒊𝒏 𝟔𝟎 𝒔 ) 𝟖𝟎𝟎 𝒎 𝒔 ∗𝟑∗𝟎,𝟎𝟏 𝒌𝒈/𝒔 = 𝟓𝟐,𝟒 𝒔 Conservación del momento angular 27. Verdadero o falso: Si el momento resultante sobre un sistema rotatorio es cero, la velocidad angular del sistema no puede modificarse. Falso. 𝝉 = ∆𝑳 ∆𝒕 = 𝑰∗∆𝝎 ∆𝒕 Si el momento de inercia cambia, podrá cambiar la velocidad angular. 28. La sabiduría popular afirma que “los gatos siempre caen de pie”. Si un gato comienza a caer con las patas hacia arriba, ¿Cómo es posible que caiga sobre sus pies sin violar el principio de conservación del momento angular? La mitad de su cuerpo genera momento de inercia hacia un lado y la otra lo genera hacia el otro, de manera que los dos se contrarrestan. Utilizando esta trampa, el
- 10. momento de inercia generado por el gato en conjunto se mantiene nulo durante la caída y el felino no viola ninguna ley de la física. Al comparar este movimiento con la vida real, se puede ver que este modelo se ajusta a la realidad. Cuando un gato cae, lo primero que hace un gato es doblar el cuerpo para que las dos secciones de su cuerpo roten sobre ejes distintos. A continuación, aprieta sus patas delanteras contra su cuerpo para reducir su momento de inercia (igual que la bailarina que acerca sus extremidades al cuerpo para girar más rápido). Al mismo tiempo extiende las patas traseras para aumentar el momento de inercia en la parte trasera de su cuerpo, lo que le ayuda a rotar la parte delantera del cuerpo hasta 90°, mientras la trasera sólo gira unos 10° durante esta fase. Por último, para que la parte trasera de su cuerpo termine de girar, el gato extiende sus patas delanteras y acerca a su cuerpo las traseras para producir el efecto inverso. 29. Si el movimiento angular de un sistema es constante, ¿Cuál de las siguientes afirmaciones es cierta? a) Ningún momento actúa sobre una parte cualquiera del sistema. b) Un momento constante actúa sobre cada una de las partes del sistema. c) Un momento resultante nulo actúa sobre cada parte del sistema. d) Un momento externo constante actúa sobre el sistema. e) Un momento resultante cero actúa sobre el sistema. Si L es constante, sabemos que el par neto que actúa sobre el sistema es cero. La € es correcta. 30. Dos discos cilíndricos idénticos poseen un eje común. Inicialmente uno de ellos está girando. Cuando ambos discos se ponen en contacto se adhieren entre sí. ¿Cuál de las siguientes afirmaciones es cierta? a) La energía cinética total y el momento angular total son invariables e iguales a sus valores iniciales. b) La energía cinética total y el momento angular total se reducen a la mitad de sus valores originales. c) El momento angular total es invariable, ero la energía cinética total se reduce a la mitad de su valor original. d) El momento angular total se reduce a la mitad de su valor original, pero la energía cinética total es invariable. e) El momento angular total es invariable y la energía cinética total se reduce a un cuarto de su valor original. La a es la correcta al ser un sistema aislado. 31. En el ejemplo siguiente, ¿realiza trabajo la fuerza ejercida por el tiovivo sobre la niña? Ejemplo: Un tiovivo de radio 2 m y momento de inercia 500 kg m2 está girando alrededor de un pivote sin rozamiento a razón de una revolución cada 5 s. Una niña de masa 25 kg que originalmente se encuentra de pie en el centro del tiovivo, se desplaza hacia el borde. La persona camina radialmente, la fuerza de fricción no realiza trabajo, se produce un cambio en el momento de inercia del sistema y eso produce el giro, la energía del sistema y el momento angular se conservan.
- 11. 32. En un tiovivo en rotación, ¿qué es más fácil: andar radialmente hacia fuera o andar radialmente hacia dentro? ¿Por qué? Al girar el tiovivo la fuerza resultante sobre la persona estará dirigida hacia dentro, fuerza centrípeta. Al ir hacia fuera aumenta el momento de inercia y disminuye la velocidad de rotación, con ello también baja la fuerza resultante. Al ir hacia dentro aumenta la velocidad y con ello aumenta la fuerza resultante. Será más fácil caminar hacia afuera. 33. Un bloque que se desliza sobre una mesa sin rozamiento está atado a una cuerda que pasa por un agujero de la mesa. Inicialmente el bloque se desliza con velocidad vo sobre una circunferencia de radio ro. Una persona bajo la mesa tira lentamente de la cuerda. ¿Qué ocurre cuando el bloque gira en espiral hacia dentro? (Razonar con argumentos la respuesta correcta) a) Su energía y momento angular se conservan. b) Su momento angular se conserva y su energía crece. c) Su momento angular se conserva y su energía decrece. d) Su energía se conserva y su momento angular crece. e) Su energía se conserva y su momento angular decrece. La opción b es la correcta, el momento de la fuerza aplicada es nulo, por tanto, L se conserva. En cambio, al disminuir I aumenta la velocidad de rotación y con ello la energía cinética del bloque. 34. Un planeta se mueve en una órbita elíptica alrededor del Sol, estando éste en un foco de la elipse (figura). a) ¿Cuál es el momento producido por la fuerza gravitatoria de atracción del Sol sobre el planeta? b) En la posición A, el planeta está a una distancia r1 del Sol y se está moviendo con velocidad v1 perpendicular a la línea que va del Sol al planeta. En la posición B, está a una distancia r2 y se mueve con velocidad v2, de nuevo perpendicular a la línea que va del Sol al planeta. ¿Cuál es la relación de v1 y v2 en función de r1 y r2? El momento de las fuerzas que actúan será cero l ser estas radiales, por tanto, el momento angular se mantiene constante. 𝒎 ∗ 𝒗𝟏 ∗ 𝒓𝟏 = 𝒎 ∗ 𝒗𝟐 ∗ 𝒓𝟐 𝒗𝟏 𝒗𝟐 = 𝒓𝟐 𝒓𝟏 35. Una estrella giratoria esférica de densidad uniforme se colapsa gravitatoriamente (todas las fuerzas apuntan hacia el centro), con lo cual su radio se reduce a a mitad y su densidad crece de modo uniforme en toda la estrella. ¿Qué relación existe entre la velocidad angular final de la estrella ω2, y su velocidad angular ω1? a) 2 b) 0,5 c) 4 d) 0,25 e) 1,0 El momento angular se mantiene constante. 𝑰𝟏 ∗ 𝝎𝟏 = 𝑰𝟐 ∗ 𝒘𝟐
- 12. Utilizando el momento de inercia de la esfera: 𝟐 𝟓 ∗ 𝑴 ∗ 𝑹𝟏 𝟐 ∗ 𝝎𝟏 = 𝟐 𝟐 ∗ 𝑴 ∗ 𝑹𝟐 𝟐 ∗ 𝝎𝟐 𝝎𝟐 𝝎𝟏 = 𝑹𝟏 𝟐 /𝑹𝟐 𝟐 = 𝟒 Respuesta d. 36. Un hombre está de pie sobre una plataforma sin rozamiento que gira con una velocidad angular de 1,5 rev/s. Sus brazos están extendidos y sostiene en cada mano una bola pesada. El momento de inercia del hombre, los pesos extendidos y la plataforma es 6 kg m2 . Cuando el hombre impulsa los pesos hacia su cuerpo, el momento de inercia decrece a 1,8 kg m2 . a) ¿Cuál es la velocidad angular resultante de la plataforma? b) ¿Cuál es la variación de energía cinética experimentada por el sistema? c) ¿De dónde procede este incremento de energía? a) 𝑰𝟏 ∗ 𝝎𝟏 = 𝑰𝟐 ∗ 𝒘𝟐 𝝎𝟐 = 𝑰𝟏∗𝝎𝟏 𝑰𝟐 = 𝟔∗𝟏,𝟓 𝒓𝒆𝒗/𝒔 𝟏,𝟖 = 𝟓,𝟎 𝒓𝒆𝒗/𝒔 b) ∆𝑬𝒄 = 𝟏 𝟐 ∗ (𝑰𝟐 ∗ 𝝎𝟐 𝟐 − 𝑰𝟏 ∗ 𝝎𝟏 𝟐 ) = 𝟏 𝟐 ∗ (𝟏,𝟖 ∗ 𝟓, 𝟎𝟐 − 𝟔 ∗ 𝟏, 𝟓𝟐) = 𝟔𝟐𝟐 𝑱 c) La energía procede del hombre que ha producido un movimiento (energía interna del hombre). 37. Una pequeña porción de masilla de masa m cae desde el techo sobre el borde exterior de un tocadiscos de radio R y momento de inercia Io, que está girando libremente con velocidad angular 𝝎𝒊 alrededor de su eje de simetría vertical fijo. a) ¿Cuál es la velocidad angular del tocadiscos más la masilla después del choque? b) Después de varias vueltas, la masilla se desprende del borde del tocadiscos hacia fuera. ¿Cuál es la velocidad angular del tocadiscos después de desprenderse la masilla? a) 𝑰𝒐 ∗ 𝝎𝒊 = 𝑰𝟐 ∗ 𝒘𝟐 𝝎𝟐 = 𝑰𝒐∗𝝎𝒊 𝑰𝟐 El momento de inercia final es: 𝑰𝟐 = 𝒎 ∗ 𝑹𝟐 + 𝑰𝒐 𝝎𝟐 = 𝑰𝒐∗𝝎𝒊 𝒎∗𝑹𝟐+𝑰𝒐 b) La masilla se desprende del tocadiscos con la velocidad de giro que tenía este, por tanto, en el momento de la salida de esta el momento de inercia del sistema es el mismo que tenía y, por tanto, la velocidad angular será la misma que tenía, ω2. 38. Dos discos de masa idéntica, pero de radios diferentes (r y 2 r) giran sobre cojinetes sin rozamiento a la misma velocidad angular wo, pero en sentidos opuestos (figura). Lentamente los dos discos son impulsados el uno hacia el otro hasta que sus superficies entran en contacto. La fuerza de rozamiento superficial da lugar a que eventualmente ambos posean la misma velocidad angular. ¿Cuál es la magnitud de esta velocidad angular final?
- 13. 𝑰𝟏 ∗ 𝝎𝟏 = 𝑰𝟐 ∗ 𝒘𝟐 La cantidad de movimiento inicial es: 𝟏 𝟐 ∗ 𝒎 ∗ 𝟒 ∗ 𝒓𝟐 ∗ 𝝎𝒐 − 𝟏 𝟐 ∗ 𝒎 ∗ 𝒓𝟐 ∗ 𝝎𝒐 = ( 𝟏 𝟐 ∗ 𝒎 ∗ 𝟒 ∗ 𝒓𝟐 + 𝟏 𝟐 ∗ 𝒎 ∗ 𝒓𝟐) ∗ 𝝎𝟐 𝝎𝟐 = 𝟑 𝟑 ∗ 𝝎𝒐 39. Un bloque de masa m que desliza sobre una mesa sin rozamiento está atado a una cuerda que pasa por un agujero dela mesa. Inicialmente el bloque desliza con velocidad vo en un círculo de radio ro. Determinar a) El momento angular del bloque. b) Su energía cinética. c) La tensión de la cuerda. Una persona situada bajo la mesa, tira suavemente de la cuerda. ¿Cuánto trabajo se necesita para reducir el radio del círculo de ro a ro/2? a) 𝑳 = 𝒎 ∗ 𝒗𝒐 ∗ 𝒓𝒐 b) 𝑬𝒄 = 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝒐 𝟐 c) La tensión de la cuerda será la fuerza centrípeta. 𝑻 = 𝒎 ∗ 𝒗𝒐 𝟐 𝒓𝒐 Al cambiar de radio la masa cambia de velocidad, conservándose el momento angular del bloque. 𝒎 ∗ 𝒓𝒐 𝟐 ∗ 𝒗𝒐 𝒓𝒐 = 𝒎 ∗ 𝒓𝒐 𝟐 𝟒 ∗ 𝒗 𝒓𝒐 𝟐 ⁄ 𝒗 = 𝟐 ∗ 𝒗𝒐 𝑾 = ∆𝑬𝒄 = 𝟏 𝟐 ∗ 𝒎 ∗ 𝟒 ∗ 𝒗𝒐 𝟐 − 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝒐 𝟐 = 𝟑 𝟐 ∗ 𝒎 ∗ 𝒗𝒐 𝟐 40. Al comienzo de cada curso, un profesor de física llamado Dr. Zeus realiza una demostración que él llama “Lección #1”. Se coloca en el centro de una plataforma rotatoria que gira sin rozamiento. Toma entonces un globo terrestre de 2 kg atado al extremo de una cadena de 0,8 m de longitud y lo hace girar alrededor de su cabeza. El “mundo” gira a su alrededor una vuelta completa cada 3 s, y el profesor y la plataforma tiene un momento de inercia de 0,5 kg m2 . a) ¿Cuál es la velocidad angular del profesor? b) ¿Cuál es la energía cinética total del globo, profesor y plataforma? a) Suponemos que la longitud de la cuerda indica el radio del globo terrestre. 𝟎 = 𝑰𝒈 ∗ 𝝎𝒈 + 𝑰𝒑 ∗ 𝒘𝒑 𝒘𝒑 = − 𝑰𝒈∗𝝎𝒈 𝑰𝒑 = − 𝟐 𝟓 ∗𝒎∗𝒓𝟐∗𝝎𝒈 𝑰𝒑 = − 𝟐 𝟓 ∗𝟐∗𝟎,𝟖𝟐∗ 𝟐∗𝝅 𝒓𝒂𝒅 𝟑 𝒔 𝟎,𝟓 = −𝟐,𝟏𝟒 𝒓𝒂𝒅/𝒔 b) 𝑬𝒄 = 𝟏 𝟐 ∗ 𝑰𝒈 ∗ 𝝎𝒈 𝟐 + 𝟏 𝟐 ∗ 𝑰𝒑 ∗ 𝝎𝒑 𝟐 = 𝟏 𝟐 ∗ 𝟐 𝟓 ∗ 𝟐 ∗ 𝟎,𝟖𝟐 ∗ ( 𝟐∗𝝅 𝒓𝒂𝒅 𝟑 𝒔 ) 𝟐 + 𝟏 𝟐 ∗ 𝟎, 𝟓 ∗ 𝟐.𝟏𝟒𝟐 = 𝟐,𝟐𝟕 𝑱 41. El radio del Sol es 6,96 108 m y gira sobre si mismo con un período de 25,3 d. Estimar el periodo de rotación que tendría el Sol si se colapsara sin pérdida de masa hasta convertirse en una estrella de neutrones de radio 5 km. 𝑰𝟏 ∗ 𝝎𝟏 = 𝑰𝟐 ∗ 𝒘𝟐 𝟐 𝟓 ∗ 𝑴 ∗ 𝑹𝟏 𝟐 ∗ 𝝎𝟏 = 𝟐 𝟓 ∗ 𝑴 ∗ 𝑹𝟐 𝟐 ∗ 𝝎𝟐 𝝎𝟐 = 𝑹𝟏 𝟐 ∗ 𝝎𝟏 𝑹𝟐 𝟐 = (𝟔,𝟗𝟔 ∗ 𝟏𝟎𝟖 )𝟐 ∗ 𝟏 𝒗𝒖𝒆𝒍𝒕𝒂/𝟐𝟓,𝟑 𝒅𝒊𝒂𝒔 𝟓𝟎𝟎𝟎𝟐 = 𝟕,𝟔𝟔 𝟏𝟎𝟖 𝒗𝒖𝒆𝒍𝒕𝒂𝒔/𝒅𝒊𝒂
- 14. 𝑻 = 𝟏 𝟕,𝟔𝟔 𝟏𝟎𝟖 = 𝟏,𝟑𝟏 𝟏𝟎−𝟗 𝒅𝒊𝒂𝒔 42. Al llegar al área de recogida de equipajes de un pequeño aeropuerto, un joven de masa m descubre una plataforma rotatoria (radio r y momento de inercia I) que está girando sin control. El joven salta sobre el borde de la plataforma que continúa girando libremente con una velocidad angular de 7,5 rad/s. Luchando con sus manos y rodillas consigue llegar al centro de la plataforma donde se pone de pie y adopta una postura que recuerda a un bailarín girando sobre sí mismo. Los pasajeros aplauden y alguien avisa a los servicios de seguridad. Suponer que mR2 =2,8 I y que el joven tiene un momento de inercia I/10 en su posición final. ¿Cuál es su velocidad angular final si se desprecia el rozamiento? 𝑰𝟏 ∗ 𝝎𝟏 = 𝑰𝟐 ∗ 𝒘𝟐 𝒘𝟐 = 𝑰𝟏∗𝝎𝟏 𝑰𝟐 = (𝒎∗𝑹𝟐+𝑰)∗𝝎𝟏 𝑰 𝟏𝟎 +𝑰 = (𝟐,𝟖∗𝑰+𝑰)∗𝝎𝟏 𝟏𝟏 𝟏𝟎 ∗𝑰 = 𝟑,𝟖∗𝟕,𝟓 𝟏𝟏/𝟏𝟎 = 𝟐𝟓,𝟗 𝒓𝒂𝒅/𝒔 43. Una masa puntual de 0,2 kg que se mueve sobre una superficie horizontal sin rozamiento está atada a una cinta de caucho cuyo otro extremo está fio en el punto P. La cinta de caucho ejerce una fuerza F=bx hacia P en donde x es la longitud de la cinta y b un coeficiente desconocido. La masa se mueve a lo largo de la línea de puntos de la figura. Cuando pasa por el punto A su velocidad es de 4 m/s en la dirección que se muestra. La distancia AP es de 0,6 m y BP es 1,0 m. a) Determinar la velocidad de la masa en los puntos B y C. b) Determinar el coeficiente b. a) 𝑳𝑨 = 𝑳𝑩 = 𝑳𝑪 𝒎 ∗ 𝒗𝑨 ∗ 𝒓𝑨 = 𝒎 ∗ 𝒗𝑩 ∗ 𝒓𝑩 = 𝒎 ∗ 𝒗𝑪 ∗ 𝒓𝑪 𝒗𝑩 = 𝒗𝑨∗𝒓𝑨 𝒓𝑩 = 𝟒∗𝟎,𝟔 𝟏 = 𝟐,𝟒 𝒎/𝒔 𝒗𝑪 = 𝒗𝑨∗𝒓𝑨 𝒓𝑪 = 𝟒∗𝟎,𝟔 𝟎,𝟔 = 𝟒 𝒎/𝒔 b) 𝑳𝒂 𝒇𝒖𝒆𝒓𝒛𝒂 𝒃𝒙 𝒆𝒔 𝒄𝒐𝒏𝒔𝒆𝒓𝒗𝒂𝒕𝒊𝒗𝒂 ,𝒚 𝒍𝒂 𝒆𝒏𝒆𝒓𝒈𝒊𝒂 𝒑𝒐𝒕𝒆𝒏𝒄𝒊𝒂𝒍 𝒂𝒔𝒐𝒄𝒊𝒂𝒅𝒂 𝒆𝒔 𝟏 𝟐 𝒃𝒙𝟐 . Aplicando el principio de conservación de la energía mecánica: 𝑬𝑨 = 𝑬𝑩 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝑨 𝟐 + 𝟏 𝟐 ∗ 𝒃 ∗ 𝒙𝑨 𝟐 = 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝑩 𝟐 + 𝟏 𝟐 ∗ 𝒃 ∗ 𝒙𝑩 𝟐 𝒃 = 𝒎∗(𝒗𝑨 𝟐 −𝒗𝑩 𝟐 ) 𝒙𝑩 𝟐 −𝒙𝑨 𝟐 = 𝟎,𝟐∗(𝟒𝟐−𝟐,𝟒𝟐) 𝟏𝟐−𝟎,𝟔𝟐 = 𝟑,𝟐 𝑵/𝒎 Cuantización del momento angular
- 15. 44. Una partícula de 2 kg se mueve con velocidad constante de 3 mm/s alrededor de un círculo de radio 4 mm. a) Determinar la magnitud del momento angular de la partícula. b) Si 𝑳 = √𝒍(𝒍 + 𝟏)ℏ determinar el valor de l(l+1) y el valor aproximado de l. c) Explicar por qué la cuantización del momento angular no se observa en la física macroscópica. a) 𝑳 = 𝒎 ∗ 𝒗 ∗ 𝒓 = 𝟐 ∗ 𝟎,𝟎𝟎𝟑 ∗ 𝟎, 𝟎𝟎𝟒 = 𝟐, 𝟒 ∗ 𝟏𝟎−𝟓 𝒌𝒈 𝒎𝟐 /𝒔 b) 𝒍 ∗ (𝒍 + 𝟏) = 𝑳𝟐 ℏ𝟐 = (𝟐,𝟒∗𝟏𝟎−𝟓) 𝟐 (𝟏,𝟎𝟓∗𝟏𝟎−𝟑𝟒)𝟐 = 𝟓 ∗ 𝟏𝟎𝟓𝟖 𝒍 ∼ 𝟐 ∗ 𝟏𝟎𝟑𝟒 c) Estamos hablando de un sistema con un momento angular que es del orden de 1034 veces mayor que el valor fundamental, no apreciable. 45. El componente z del spin de un electrón es ½ ℏ, pero la magnitud del vector spin es √𝟎,𝟕𝟓ℏ. ¿Qué ángulo forma el vector momento angular de spin del electrón con el eje z? 𝜽 = 𝒂𝒓𝒄𝒄𝒐𝒔 ( 𝟏 𝟐 √𝟎,𝟕𝟓 ) = 𝟓𝟒,𝟕𝒐 46. Demostrar que la diferencia energética entre un estado rotacional y el siguiente estado más elevado es proporcional a l+1. La energía cinética de un cuerpo en rotación es: 𝑬𝒄 = 𝑳𝟐 𝟐∗𝑰 Como L está cuantizado 𝑳𝟐 = 𝒍 ∗ (𝒍 + 𝟏) ∗ ℏ𝟐 ; con l=0,1,2… 𝑬𝒄 = 𝑳𝟐 𝟐∗𝑰 = 𝒍 ∗ (𝒍 + 𝟏) ∗ 𝑬𝟎𝒓 Donde: 𝑬𝟎𝒓 = ℏ𝟐 𝟐∗𝑰 Por tanto: ∆𝑬𝒄 = ((𝒍 + 𝟏) ∗ (𝒍 + 𝟐)−𝒍 ∗ (𝒍 + 𝟏)) ∗ 𝑬𝟎𝒓 = 𝟐 ∗ (𝒍 + 𝟏) ∗ 𝑬𝟎𝒓 47. En la molécula HBr la masa del núcleo de bromo es 80 veces superior a la masa del núcleo de hidrógeno (un solo protón); en consecuencia, al estudiar el movimiento rotacional de esta molécula, es correcto suponer, con buena aproximación, que el núcleo de Br permanece estacionario mientras el átomo de H (masa 1,67 10-27 kg) gira a su alrededor. La separación entre el átomo de H y el núcleo de Br es 0,144 nm. Calcular a) El momento de inercia de la molécula HBr respecto al núcleo de Br. b) Las energías de rotación correspondientes a l=1, l=2 y l=3.
- 16. a) 𝑰 = 𝒎𝒑 ∗ 𝒓𝟐 = 𝟏, 𝟔𝟕 ∗ 𝟏𝟎−𝟐𝟕 ∗ (𝟎,𝟏𝟒𝟒 ∗ 𝟏𝟎−𝟗) 𝟐 = 𝟑, 𝟒𝟔 ∗ 𝟏𝟎−𝟒𝟕 𝒌𝒈 𝒎𝟐 b) 𝑬𝟎𝒓 = ℏ𝟐 𝟐∗𝑰 = (𝟏,𝟎𝟓∗𝟏𝟎−𝟑𝟒)𝟐 𝟐∗𝟑,𝟒𝟔∗𝟏𝟎−𝟒𝟕 = 𝟏,𝟓𝟗 ∗ 𝟏𝟎−𝟐𝟐 𝑱 𝑬𝟏 = 𝟏 ∗ (𝟏 + 𝟏) ∗ 𝟏,𝟓𝟗 ∗ 𝟏𝟎−𝟐𝟐 = 𝟑,𝟐 ∗ 𝟏𝟎−𝟐𝟐 𝑱 𝑬𝟐 = 𝟐 ∗ (𝟐 + 𝟏) ∗ 𝟏,𝟓𝟗 ∗ 𝟏𝟎−𝟐𝟐 = 𝟗,𝟓𝟒 ∗ 𝟏𝟎−𝟐𝟐 𝑱 𝑬𝟑 = 𝟑 ∗ (𝟑 + 𝟏) ∗ 𝟏,𝟓𝟗 ∗ 𝟏𝟎−𝟐𝟐 = 𝟏𝟗,𝟏 ∗ 𝟏𝟎−𝟐𝟐 𝑱 48. La separación de equilibrio entre los núcleos de la molécula de nitrógeno es 0,11 nm. La masa de cada núcleo de nitrógeno es 14 u, en donde u=1,66 10-27 kg. Deseamos calcular las energías de los tres estados de la molécula de nitrógeno de menor momento angular. a) Considerar un modelo de la molécula de nitrógeno formado por una pesa de gimnasia, rígida, con dos masas puntuales iguales en sus extremos y calcular el momento de inercia alrededor de su centro de masas. b) Determinar los niveles energéticos de rotación mediante la relación 𝑬𝒍 = 𝒍(𝒍 + 𝟏)ℏ𝟐 /𝟐𝑰. a) 𝑰 = 𝟐 ∗ 𝒎𝑵 ∗ 𝒓𝟐 Donde 𝒓 = 𝟎,𝟏𝟏 𝟐 𝒏𝒎 = 𝟎,𝟎𝟓𝟓 𝒏𝒎. 𝑰 = 𝟐 ∗ 𝟏𝟒 ∗ 𝟏,𝟔𝟔 ∗ 𝟏𝟎−𝟐𝟕 ∗ (𝟎, 𝟎𝟓𝟓 ∗ 𝟏𝟎−𝟗 )𝟐 = 𝟏,𝟒𝟏 ∗ 𝟏𝟎−𝟒𝟔 𝒌𝒈 𝒎𝟐 b) 𝑬𝟎𝒓 = ℏ𝟐 𝟐∗𝑰 = (𝟏,𝟎𝟓∗𝟏𝟎−𝟑𝟒)𝟐 𝟐∗𝟏,𝟒𝟏∗𝟏𝟎−𝟒𝟔 = 𝟑,𝟗𝟏 𝟏𝟎−𝟐𝟑 𝑱 𝑬𝒍 = 𝒍 ∗ (𝒍 + 𝟏) ∗ 𝟑,𝟗𝟏 𝟏𝟎−𝟐𝟑 𝑱 Colisiones 49. Una barra de 16,0 kg y 2,4 m de longitud está apoyada sobre el filo de una cuchilla en su punto medio. Una bola de 3,2 kg de arcilla se deja caer desde el reposo, de una altura de 1,2 m y produce un choque con la barra completamente inelástico a 0,9 m del punto de soporte (figura). Determinar el momento angular del sistema barra más arcilla, inmediatamente después de la colisión inelástica. Por la conservación de la energía mecánica: 𝒎𝟏 ∗ 𝒈 ∗ 𝒉 = 𝟏 𝟐 ∗ 𝒎𝟏 ∗ 𝒗𝟐 , 𝒗 = √𝟐 ∗ 𝒈 ∗ 𝒉 Por colisión inelástica: 𝒎𝟏 ∗ √𝟐 ∗ 𝒈 ∗ 𝒉 = (𝒎𝟏 + 𝒎𝟐) ∗ 𝒗𝒇 𝒗𝒇 = 𝒎𝟏∗√𝟐∗𝒈∗𝒉 (𝒎𝟏+𝒎𝟐) El momento angular del sistema será: 𝑳 = (𝒎𝟏 + 𝒎𝟐) ∗ 𝒗𝒇 ∗ 𝒓 = (𝒎𝟏 + 𝒎𝟐) ∗ 𝒎𝟏∗√𝟐∗𝒈∗𝒉 (𝒎𝟏+𝒎𝟐) ∗ 𝒓 = 𝒎𝟏 ∗ √𝟐 ∗ 𝒈 ∗ 𝒉 ∗ 𝒓 𝑳 = 𝟑,𝟐 ∗ √𝟐 ∗ 𝟗,𝟖𝟏 ∗ 𝟏,𝟐 ∗ 𝟎, 𝟗 = 𝟏𝟒,𝟎 𝒌𝒈 𝒎𝟐 /𝒔
- 17. 50. La figura muestra una barra delgada de longitud L y masa M y una pequeña cantidad de masilla de masa m. El sistema está apoyado sobre una superficie horizontal sin rozamiento. La masilla se mueve hacia la derecha con velocidad v, choca contra la barra a una distancia d del centro de la misma y se adhiere en el punto de contacto. Determinar las expresiones correspondientes a la velocidad del centro de masas del sistema y a la velocidad angular del sistema respecto a su centro de masas. Considerando la colisión: 𝒎 ∗ 𝒗 = (𝑴 + 𝒎) ∗ 𝒗𝒇; 𝒗𝒇 = 𝒎∗𝒗 (𝑴+𝒎) La velocidad del centro de masas será la encontrada dad que todo el sistema se mueve unido. Para determinar la velocidad angular respecto al centro de masas primero determinamos la posición de éste, tomamos como origen de coordenadas la parte inferior de la barra: 𝒚𝒄𝒎 = 𝒎∗𝒅 𝑴+𝒎 ; 𝒕𝒆𝒏𝒅𝒓𝒊á 𝒔𝒊𝒈𝒏𝒐 La velocidad angular buscada será: 𝝎𝒄𝒎 = 𝑳𝒄𝒎 𝑰𝒄𝒎 𝑳𝒄𝒎 = 𝒎 ∗ 𝒗 ∗ 𝒓 = 𝒎 ∗ 𝒗 ∗ (𝒅 − 𝒚𝒄𝒎) = 𝒎 ∗ 𝒗 ∗ 𝒅∗𝑴 𝑴+𝒎 𝑰𝒄𝒎 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝑴 ∗ 𝒚𝒄𝒎 𝟐 + 𝒎 ∗ (𝒅 − 𝒚𝒄𝒎)𝟐 𝑰𝒄𝒎 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝑴 ∗ ( 𝒎∗𝒅 𝑴+𝒎 ) 𝟐 + 𝒎 ∗ ( 𝒅∗𝑴 𝑴+𝒎 ) 𝟐 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + (𝑴+𝒎)∗𝒎∗𝑴∗𝒅𝟐 (𝒎+𝑴)𝟐 𝑰𝒄𝒎 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝒎∗𝑴∗𝒅𝟐 𝒎+𝑴 Por tanto: 𝝎𝒄𝒎 = 𝑳𝒄𝒎 𝑰𝒄𝒎 = 𝒎∗𝒗∗ 𝒅∗𝑴 𝑴+𝒎 𝟏 𝟏𝟐 ∗𝑴∗𝑳𝟐+ 𝒎∗𝑴∗𝒅𝟐 𝒎+𝑴 = 𝒎∗𝒗∗𝒅∗𝑴 𝟏 𝟏𝟐 ∗𝑴∗𝑳𝟐∗(𝑴+𝒎)+𝒎∗𝑴∗𝒅𝟐 51. En el problema 50, reemplazar la bola de masilla por una pequeña esfera dura de tamaño despreciable que choca elásticamente contra la barra. Determinar el valor de d para que la esfera quede en reposo después del choque. Consideramos: Conservación de la cantidad de movimiento: 𝒎 ∗ 𝒗 = 𝑴 ∗ 𝑽′ Conservación de la cantidad de movimiento angular: 𝒎 ∗ 𝒗 ∗ 𝒅 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 ∗ 𝝎 Conservación de la energía:
- 18. 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝟐 = 𝟏 𝟐 ∗ 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 ∗ 𝝎𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ 𝑽′𝟐 Despejamos V’ de la primera y 𝝎 de la segunda, substituimos en la tercera. 𝑽′ = 𝒎∗𝒗 𝑴 𝝎 = 𝟏𝟐∗𝒎∗𝒗∗𝒅 𝑴∗𝑳𝟐 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝟐 = 𝟏 𝟐 ∗ 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 ∗ ( 𝟏𝟐∗𝒎∗𝒗∗𝒅 𝑴∗𝑳𝟐 ) 𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ ( 𝒎∗𝒗 𝑴 ) 𝟐 Obtenemos: 𝒅 = 𝑳 ∗ √ 𝑴−𝒎 𝟏𝟐∗𝒎 52. La figura muestra una barra uniforme de longitud L y masa M pivotada en la parte superior. La barra, inicialmente en reposo, recibe el choque de una partícula de masa m en un punto d=0,8L por debajo del pivote. Suponer que el choque es totalmente inelástico. ¿Cuál debe ser la magnitud de la velocidad v de la partícula para que el ángulo máximo entre la barra y la vertical sea de 90º? Considerando la conservación de la energía después del choque, d=x=0,8*L: 𝟏 𝟐 ∗ 𝑰 ∗ 𝝎𝟐 = (𝑴 ∗ 𝒈 ∗ 𝑳 𝟐 + 𝒎 ∗ 𝒈 ∗ 𝒅) ∗ (𝟏 − 𝒄𝒐𝒔𝜽) Por la conservación de la cantidad de movimiento angular: 𝒎 ∗ 𝒗 ∗ (𝟎,𝟖 ∗ 𝑳) = 𝑰 ∗ 𝒘 𝒎 ∗ 𝒗 ∗ (𝟎,𝟖 ∗ 𝑳) = ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟐 + 𝒎 ∗ (𝟎,𝟖 ∗ 𝑳)𝟐) ∗ 𝝎 La velocidad angular es: 𝝎 = 𝒎∗𝒗∗𝟎,𝟖∗𝑳 𝟏 𝟑 ∗𝑴∗𝑳𝟐+𝟎,𝟔𝟒∗𝒎∗𝑳𝟐 = 𝟎,𝟖∗𝒎∗𝒗∗𝑳 𝟏 𝟑 ∗𝑴∗𝑳𝟐+𝟎,𝟔𝟒∗𝒎∗𝑳𝟐 Substituimos en la primera ecuación, considerando ángulo de 90º:
- 19. 𝟏 𝟐 ∗ ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟐 + 𝒎 ∗ (𝟎, 𝟖 ∗ 𝑳)𝟐) ∗ ( 𝟎,𝟖∗𝒎∗𝒗∗𝑳 𝟏 𝟑 ∗𝑴∗𝑳𝟐+𝟎,𝟔𝟒∗𝒎∗𝑳𝟐 ) 𝟐 = (𝑴 ∗ 𝒈 ∗ 𝑳 𝟐 + 𝒎 ∗ 𝒈 ∗ 𝟎, 𝟖 ∗ 𝑳) Operando: 𝒗𝟐 = 𝟐∗(𝑴∗𝒈∗ 𝑳 𝟐 +𝒎∗𝒈∗𝟎,𝟖∗𝑳)∗( 𝟏 𝟑 ∗𝑴∗𝑳𝟐+𝟎,𝟔𝟒∗𝒎∗𝑳𝟐) 𝟎,𝟔𝟒∗𝒎𝟐∗𝑳𝟐 𝒗 = √ 𝑳∗(𝑴∗𝒈∗+𝟏,𝟔∗𝒎∗𝒈)∗( 𝟏 𝟑 ∗𝑴+𝟎,𝟔𝟒∗𝒎) 𝟎,𝟔𝟒∗𝒎𝟐 53. Si para el sistema del problema 52, L=1,2 m, M=0,8 kg y m=0,3 kg y el ángulo máximo entre la barra y la vertical es 60º, determinar la velocidad de la partícula antes del impacto. Usando las expresiones del problema anterior: 𝝎 = 𝟎,𝟖∗𝒎∗𝒗∗𝑳 𝟏 𝟑 ∗𝑴∗𝑳𝟐+𝟎,𝟔𝟒∗𝒎∗𝑳𝟐 𝟏 𝟐 ∗ ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟐 + 𝒎 ∗ (𝟎, 𝟖 ∗ 𝑳)𝟐 ) ∗ ( 𝟎, 𝟖 ∗ 𝒎 ∗ 𝒗 ∗ 𝑳 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟐 + 𝟎, 𝟔𝟒 ∗ 𝒎 ∗ 𝑳𝟐 ) 𝟐 = (𝑴 ∗ 𝒈 ∗ 𝑳 𝟐 + 𝒎 ∗ 𝒈 ∗ 𝟎, 𝟖 ∗ 𝑳) ∗ (𝟏 − 𝒄𝒐𝒔𝜽) Despejando v: 𝒗 = √ 𝒈∗(𝑴/𝟐+𝟎,𝟖∗𝒎)∗𝑰∗(𝟏−𝒄𝒐𝒔𝜽) 𝟎,𝟑𝟐∗𝒎𝟐∗𝑳 El momento de inercia es: 𝑰 = ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟐 + 𝟎, 𝟔𝟒 ∗ 𝒎 ∗ 𝑳𝟐) = 𝟎. 𝟔𝟔 𝒌𝒈 𝒎𝟐 𝒗 = √ 𝟗.𝟖𝟏∗(𝟎,𝟒+𝟎.𝟖∗𝟎,𝟑)∗𝟎.𝟔𝟔∗(𝟏−𝒄𝒐𝒔𝜽) 𝟎.𝟑𝟐∗𝟎.𝟑𝟐∗𝟏,𝟐 = 𝟕, 𝟕𝟒 𝒎/𝒔 54. Un proyectil de masa mp se mueve a velocidad constante vo hacia un disco estacionario de masa M y radio R, libre de girar alrededor de un pivote que pasa por su eje (figura). Antes del impacto, el proyectil se desplaza a lo largo de la línea situada a la distancia b por debajo del eje. El proyectil choca contra el disco y se adhiere el punto B. Tratar al proyectil como una masa puntual. a) Antes del impacto, ¿Cuál es el momento angular total Lo del proyectil y el disco alrededor del eje O? b) ¿Cuál es la velocidad angular w del sistema disco y proyectil justamente después del impacto? c) ¿Cuál es la energía cinética del sistema disco proyectil después del impacto? d) ¿Cuánta energía mecánica se pierde en esta colisión? a) 𝑳𝒊 = 𝒎𝒑 ∗ 𝒗𝒐 ∗ 𝒃
- 20. b) 𝑳𝒊 = 𝑳𝒇 𝒎𝒑 ∗ 𝒗𝒐 ∗ 𝒃 = 𝑰 ∗ 𝝎 𝝎 = 𝒎𝒑∗𝒗𝒐∗𝒃 𝑰 El momento de inercia es: 𝑰 = 𝟏 𝟐 ∗ 𝑴 ∗ 𝑹𝟐 + 𝒎𝒑 ∗ 𝒃𝟐 𝝎 = 𝒎𝒑∗𝒗𝒐∗𝒃 𝟏 𝟐 ∗𝑴∗𝑹𝟐+𝒎𝒑∗𝒃𝟐 = 𝟐∗𝒎𝒑∗𝒗𝒐∗𝒃 𝑴∗𝑹𝟐+𝟐∗𝒎𝒑∗𝒃𝟐 c) 𝑬𝒄 = 𝟏 𝟐 ∗ 𝑰 ∗ 𝝎𝟐 = 𝟏 𝟐 ∗ ( 𝟏 𝟐 ∗ 𝑴 ∗ 𝑹𝟐 + 𝒎𝒑 ∗ 𝒃𝟐 ) ∗ ( 𝟐∗𝒎𝒑∗𝒗𝒐∗𝒃 𝑴∗𝑹𝟐+𝟐∗𝒎𝒑∗𝒃𝟐) 𝟐 = (𝒎𝒑∗𝒗𝒐∗𝒃) 𝟐 𝑴∗𝑹𝟐+𝟐∗𝒎𝒑∗𝒃𝟐 d) ∆𝑬𝒄 = (𝒎𝒑∗𝒗𝒐∗𝒃) 𝟐 𝑴∗𝑹𝟐+𝟐∗𝒎𝒑∗𝒃𝟐 − 𝟏 𝟐 ∗ 𝒎𝒑 ∗ 𝒗𝒐 𝟐 = −𝒎𝒑 ∗ 𝒗𝒐 𝟐 ∗ ( 𝒎𝒑 𝟐∗𝒃𝟐 𝑴∗𝑹𝟐+𝟐∗𝒎𝒑∗𝒃𝟐 − 𝟏 𝟐 ) 55. Una barra uniforme de longitud L1 y masa M=0,75 kg se soporta con una bisagra en un extremo y puede girar libremente en el plano vertical (figura). La barra se libera del reposo en la posición indicada. De la bisagra pende una partícula de masa m=0,5 kg en el extremo de una cuerda de longitud L2. Al producirse el impulso, la partícula se adhiere a la barra. ¿Cuál debe ser la relación L2/L1 para que ϴmax=60º después de la colisión. Conservación del momento angular: 𝑳𝒊 = 𝑳𝒇 𝑰𝒐 ∗ 𝝎𝒐 = 𝑰𝒇 ∗ 𝝎𝒇 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝝎𝒐 = ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 + 𝒎 ∗ 𝑳𝟐 𝟐 ) ∗ 𝝎𝒇 La velocidad de salida después del choque: 𝝎𝒇 = 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 ∗𝝎𝒐 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐+𝒎∗𝑳𝟐 𝟐 En la caída de la barra se conserva la energía mecánica: 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 = 𝟏 𝟐 ∗ 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝝎𝒐 𝟐 + 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 𝝎𝒐 = √ 𝟑∗𝒈 𝑳𝟏 Por tanto, la velocidad después del choque es: 𝝎𝒇 = 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 ∗√ 𝟑∗𝒈 𝑳𝟏 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐+𝒎∗𝑳𝟐 𝟐 Después del choque se conserva la energía mecánica:
- 21. 𝟏 𝟐 ∗ ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 + 𝒎 ∗ 𝑳𝟐 𝟐 ) ∗ 𝝎𝒇 𝟐 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 ∗ (𝟏 − 𝒄𝒐𝒔𝜽) + 𝒎 ∗ 𝒈 ∗ 𝑳𝟐 ∗ (𝟏 − 𝒄𝒐𝒔𝜽) Para un ángulo de 60º, cos 60=0,5. 𝟏 𝟐 ∗ ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 + 𝒎 ∗ 𝑳𝟐 𝟐 ) ∗ ( 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 ∗√ 𝟑∗𝒈 𝑳𝟏 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 +𝒎∗𝑳𝟐 𝟐 ) 𝟐 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 ∗ 𝟏 𝟐 + 𝒎 ∗ 𝒈 ∗ 𝑳𝟐 ∗ 𝟏/𝟐 𝟏 𝟑 ∗𝑴𝟐∗𝑳𝟏 𝟑 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 +𝒎∗𝑳𝟐 𝟐 = 𝑴 ∗ 𝑳𝟏 𝟐 + 𝒎 ∗ 𝑳𝟐 Operando: 𝑳𝟏 𝟑 = 𝟐∗𝒎 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝑳𝟐 + 𝟑∗𝒎 𝑴 ∗ 𝑳𝟏 ∗ 𝑳𝟐 𝟐 + 𝟔∗𝒎𝟐 𝑴𝟐 ∗ 𝑳𝟐 𝟑 Dividiendo por 𝑳𝟏 𝟑 : 𝟏 = 𝟐∗𝒎 𝑴 ∗ 𝑳𝟐 𝑳𝟏 + 𝟑∗𝒎 𝑴 ∗ ( 𝑳𝟐 𝑳𝟏 ) 𝟐 + 𝟔∗𝒎𝟐 𝑴𝟐 ∗ ( 𝑳𝟐 𝑳𝟏 ) 𝟑 Usando los valores: 𝟏, 𝟑𝟑 ∗ 𝑳𝟐 𝑳𝟏 + 𝟐 ∗ ( 𝑳𝟐 𝑳𝟏 ) 𝟐 + 𝟐, 𝟔𝟕 ∗ ( 𝑳𝟐 𝑳𝟏 ) 𝟑 − 𝟏 = 𝟎 Resolviendo se obtiene el valor del cociente. 56. Si para el sistema de la figura, L1=1,2 m, M=2,0 kg y L2=0,8 m, después de la colisión inelástica, ϴmax= 37º. Determinar m. ¿Cuánta energía se disipa en esta colisión inelástica? 𝟏 𝟐 ∗ ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 + 𝒎 ∗ 𝑳𝟐 𝟐 ) ∗ ( 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 ∗√ 𝟑∗𝒈 𝑳𝟏 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐+𝒎∗𝑳𝟐 𝟐 ) 𝟐 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 ∗ (𝟏 − 𝒄𝒐𝒔𝜽) + 𝒎 ∗ 𝒈 ∗ 𝑳𝟐 ∗ (𝟏 − 𝒄𝒐𝒔𝜽) Operando: 𝑳𝟐 𝟑 ∗ (𝟏 − 𝒄𝒐𝒔𝟑𝟕) ∗ 𝒎𝟐 + ( 𝟏 𝟑 ∗ 𝑳𝟏 + 𝟏 𝟐 ∗ 𝑳𝟐) ∗ 𝑴 ∗ 𝑳𝟏 ∗ 𝑳𝟐 ∗ (𝟏 − 𝒄𝒐𝒔𝟑𝟕) ∗ 𝒎 − 𝟏 𝟔 ∗ 𝑴𝟐 ∗ 𝑳𝟏 𝟑 ∗ 𝒄𝒐𝒔𝟑𝟕 = 𝟎 𝟎, 𝟖𝟑 ∗ (𝟏 − 𝒄𝒐𝒔𝟑𝟕) ∗ 𝒎𝟐 + ( 𝟏 𝟑 ∗ 𝟏, 𝟐 + 𝟏 𝟐 ∗ 𝟎, 𝟖) ∗ 𝟐, 𝟎 ∗ 𝟏,𝟐 ∗ 𝟎, 𝟖 ∗ (𝟏 − 𝒄𝒐𝒔𝟑𝟕) ∗ 𝒎 − 𝟏 𝟔 ∗ 𝟐, 𝟎𝟐 ∗ 𝟏, 𝟐𝟑 ∗ 𝒄𝒐𝒔𝟑𝟕 = 𝟎 0,103*𝒎𝟐 + 𝟎, 𝟑𝟎𝟗 ∗ 𝒎 − 𝟎, 𝟗𝟐 = 𝟎 𝒎 = 𝟏, 𝟖𝟒 𝒌𝒈 57. Supongamos que en la figura del problema 55, m=0,4 kg , M=0,75 kg, L1=1,2 m y L2=0,8 m. ¿Qué velocidad angular mínima debe impartirse a la barra para que el sistema dé una vuelta completa alrededor de la bisagra después de lka colisión inelástica? ¿Cuánta energía se ha disipado en esta colisión inelástica? Con la conservación de energía después del choque: 𝟏 𝟐 ∗ ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 + 𝒎 ∗ 𝑳𝟐 𝟐 ) ∗ 𝝎𝒇 𝟐 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 + 𝟐 ∗ 𝒎 ∗ 𝒈 ∗ 𝑳𝟐 Por tanto, la velocidad de salida después del choque: 𝝎𝒇 = √ 𝟐∗𝑴∗𝒈∗𝑳𝟏+𝟒∗𝒎∗𝒈∗𝑳𝟐 ( 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 +𝒎∗𝑳𝟐 𝟐 ) 𝝎𝒇 = √ 𝟐∗𝟎.𝟕𝟓∗𝟗.𝟖𝟏∗𝟏.𝟐+𝟒∗𝟎.𝟒∗𝟗.𝟖𝟏∗𝟎.𝟖 ( 𝟏 𝟑 ∗𝟎.𝟕𝟓∗𝟏.𝟐𝟐+𝟎.𝟒∗𝟎.𝟖𝟐) = 𝟕. 𝟎𝟎 𝒓𝒂𝒅/𝒔
- 22. Conservación del momento angular en el choque: 𝑳𝒊 = 𝑳𝒇 𝑰𝒐 ∗ 𝝎𝒐 = 𝑰𝒇 ∗ 𝝎𝒇 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝝎𝒐 = ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 + 𝒎 ∗ 𝑳𝟐 𝟐 ) ∗ 𝝎𝒇 La velocidad de salida después del choque: 𝝎𝒐 = ( 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 +𝒎∗𝑳𝟐 𝟐 )∗𝝎𝒇 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 𝝎𝒐 = ( 𝟏 𝟑 ∗𝟎.𝟕𝟓∗𝟏.𝟐𝟐+𝟎.𝟒∗𝟎.𝟖𝟐)∗𝟕.𝟎𝟎 𝟏 𝟑 ∗𝟎.𝟕𝟓∗𝟏.𝟐𝟐 = 𝟏𝟏. 𝟗𝟖 𝒓𝒂𝒅/𝒔 En la caída de la barra se conserva la energía mecánica: 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 + 𝟏 𝟐 ∗ 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝝎𝒊 𝟐 = 𝟏 𝟐 ∗ 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝝎𝒐 𝟐 Despejamos la velocidad inicial: 𝝎𝒊 = √𝝎𝒐 𝟐 − 𝟑 ∗ 𝒈 𝑳𝟏 𝝎𝒊 = √𝟏𝟏. 𝟗𝟖 − 𝟑 ∗ 𝟗.𝟖𝟏 𝟏.𝟐 = 𝟏𝟎. 𝟗 𝒓𝒂𝒅/𝒔 Para la energía disipada en el choque: 𝑬𝒊 = 𝟏 𝟐 ∗ 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝝎𝟎 𝟐 = 𝟏 𝟔 ∗ 𝟎. 𝟕𝟓 ∗ 𝟏. 𝟐𝟐 ∗ 𝟏𝟏. 𝟗𝟖𝟐 𝑬𝒊 = 𝟐𝟓, 𝟖𝟑 𝑱 𝑬𝒇 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 + 𝟐 ∗ 𝒎 ∗ 𝒈 ∗ 𝑳𝟐 = 𝟎. 𝟕𝟓 ∗ 𝟗. 𝟖𝟏 ∗ 𝟏. 𝟐 + 𝟐 ∗ 𝟎. 𝟒 ∗ 𝟗. 𝟖𝟏 ∗ 𝟎. 𝟖 𝑬𝒇 = 𝟏𝟓, 𝟏 𝑱 ∆𝑬 = 𝟏𝟎. 𝟕 𝑱 58. Repetir el problema 56 para el caso en que la colisión entre la barra y la partícula sea elástica. Con la caída de la barra tenemos: 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 = 𝟏 𝟐 ∗ 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ∗ 𝝎𝟏 𝟐 𝝎𝟏 = √ 𝟑∗𝒈 𝑳𝟏 Para el choque elástico tendremos conservación de la energía y de la cantidad de movimiento, con la conservación de la energía usamos la potencial inicial, la cinética de la bola al salir del choque y la potencial final de la barra: 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 ∗ (𝟏 − 𝒄𝒐𝒔𝟑𝟕) + 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝟐 Despejamos 𝒎 ∗ 𝒗𝟐 𝒎 ∗ 𝒗𝟐 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 ∗ 𝒄𝒐𝒔𝟑𝟕 La subida de la barra también conserva la energía: 𝟏 𝟐 ∗ ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ) ∗ 𝝎𝟏 𝟐 = 𝑴 ∗ 𝒈 ∗ 𝑳𝟏 𝟐 ∗ (𝟏 − 𝒄𝒐𝒔𝟑𝟕) 𝝎𝟐 = √ 𝟑∗𝒈∗(𝟏−𝒄𝒐𝒔𝟑𝟕) 𝑳𝟏 En el choque se conserva la cantidad de movimiento: ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ) ∗ 𝝎𝟏 = ( 𝟏 𝟑 ∗ 𝑴 ∗ 𝑳𝟏 𝟐 ) ∗ 𝝎𝟐 + 𝒎 ∗ 𝒗 ∗ 𝑳𝟐
- 23. 𝒎 ∗ 𝒗 = ( 𝟏 𝟑 ∗𝑴∗𝑳𝟏 𝟐 )∗(𝝎𝟏−𝝎𝟐) 𝑳𝟐 Usando las expresiones de mv y mv2 : 𝒗 = 𝒎∗𝒗𝟐 𝒎∗𝒗 = 𝟑∗𝒈∗𝑳𝟐∗𝒄𝒐𝒔𝟑𝟕 𝑳𝟏∗(𝝎𝟏−𝝎𝟐) = 𝟑∗𝒈∗𝑳𝟐∗𝒄𝒐𝒔𝟑𝟕 𝑳𝟏∗(√ 𝟑∗𝒈 𝑳𝟏 −√ 𝟑∗𝒈∗(𝟏−𝒄𝒐𝒔𝟑𝟕) 𝑳𝟏 ) 𝒗 = 𝟑∗𝟗,𝟖∗𝟎,𝟖∗𝒄𝒐𝒔𝟑𝟕 𝟏,𝟐∗(√ 𝟑∗𝟗,𝟖 𝟏,𝟐 −√ 𝟑∗𝟗,𝟖∗(𝟏−𝒄𝒐𝒔𝟑𝟕) 𝟏,𝟐 ) = 𝟓, 𝟕𝟐 𝒎/𝒔 Por tanto: cos37 𝒎 = 𝑴∗𝒈∗𝑳𝟏∗𝒄𝒐𝒔𝟑𝟕 𝒗𝟐 = 𝟐∗𝟗,𝟖∗𝟏,𝟐∗𝒄𝒐𝒔𝟑𝟕 𝟓,𝟕𝟐𝟐 = 𝟎, 𝟓𝟕𝟓 𝒌𝒈 La energía se ha de mantener constante todo el proceso para todo el sistema al ser un choque elástico. Movimiento de un giroscopio 59. Verdadero o falso: a) La nutación y la precesión son el mismo fenómeno. b) El sentido de la precesión es el mismo que posee el momento resultante. c) Si el giroscopio no está girando 𝝉 = 𝒅𝑳 𝒅𝒕 no es válida. a) Falso b) Verdadero c) Falso 60. El vector momento angular de una rueda que gira alrededor de su eje está dirigido a lo largo del eje y apunta hacia el este. Para que este vector apunte al sur es necesario ejercer una fuerza en el extremo este del eje en dirección a) Hacia arriba b) Hacia abajo c) Hacia el norte d) Hacia el norte e) Hacia el este Correcta la b. 61. Un hombre que pasea hacia el norte, lleva una caja que contiene un giroscopio en movimiento de giro, montado sobre un eje apoyado en la parte delantera y trasera de la caja. La velocidad angular del giroscopio apunta al norte. El hombre comienza a girar para continuar su paseo hacia el este. En consecuencia, el extremo frontal de la caja a) Se resiste al intento de giro y tratará de permanecer apuntando al norte. b) Luchará contra el intento de giro y empujará hacia el oeste. c) Se elevará hacia arriba. d) Se hundirá hacia abajo. e) No experimentará ningún efecto. Respuesta d. 62. El momento angular de la hélice de un pequeño aeroplano está dirigido hacia adelante.
- 24. a) Mientras el aeroplano despega, su parte delantera se levanta y tiende a virar hacia un lado, ¿hacia qué lado y por qué? b) Si el aeroplano se encuentra volando horizontalmente y de repente gira hacia la derecha, ¿su parte delantera tiende a moverse hacia arriba o hacia abajo?¿Por qué? a) Hacia la derecha, el hecho de despegar hace girar el momento angular hacia arriba, el giro es en respuesta al par asociado al despegue. b) El vector momento angular gira hacia la derecha, el par apunta hacia abajo, la punta se mueve hacia abajo. 63. Un automóvil funciona con la energía almacenada en un solo volante de momento angular L. Analizar los problemas que surgirían para distintas orientaciones de L y diversas maniobras del coche. Por ejemplo. ¿qué ocurriría si L apunta verticalmente hacia arriba y el coche sube por una colina o desciende por un valle? ¿Qué ocurriría si l apunta si L apunta hacia delante o hacia un lado del coche y éste intenta girar a la izquierda o a la derecha? En cada caso que se analice, considerar el sentido del momento ejercido sobre el coche por la carretera. Imaginar que L apunta verticalmente hacia arriba y el coche se mueve alejándose del observador dando la vuelta a la parte alta de una colina. El vector original L se altera por la adición de un ∆L apuntando hacia la izquierda; por tanto, L gira en sentido antihorario y el coche rueda hacia su izquierda. Si L hubiera apuntado hacia abajo, el mismo ∆L se habría sumado, pero produciendo una rotación en sentido horario de L y un giro del coche hacia la derecha. Si L apunta hacia delante, el coche se aleja del observador y gira hacia la izquierda. El momento ejercido por el suelo sobre el coche en este caso apunta hacia arriba. Esto significa que un componente hacia arriba del momento angular se suma a L, tendiendo a levantar la parte frontal del coche. Si L apuntase hacia atrás, el mismo giro a la izquierda daría lugar a mismo incremento del momento angular, pero ahora se elevaría la parte trasera del coche. 64. Una rueda de bicicleta está montada en el punto medio de un eje de 50 cm de largo. El neumático y la llanta pesan 30 N y tiene un radio de 28 cm. La rueda se hace girar a 12 rev/s y el eje se coloca entonces en una posición horizontal con uno de sus extremos descansando sobre un pivote. a) ¿Cuál es su momento angular debido al giro sobre sí mismo de la rueda? (Considérese que la rueda es un aro). b) ¿Cuál es la velocidad angular de precesión? c) ¿Cuánto tiempo has de transcurrir para que el eje recorra los 360º alrededor del pivote? d) ¿Cuál es el momento angular asociado con el movimiento del centro de masas, es decir, debido a la precesión? ¿En qué dirección actúa este momento angular? a) 𝑳 = 𝑰 ∗ 𝝎 = 𝑴 ∗ 𝑹𝟐 ∗ 𝝎 = 𝟑𝟎 𝟗,𝟖 ∗ 𝟎, 𝟐𝟖 ∗ 𝟏𝟐𝒓𝒆𝒗 𝒔 ∗ 𝟐 𝝅 𝒓𝒂𝒅 𝟏 𝒓𝒆𝒗 = 𝟏𝟖, 𝟏 𝒌𝒈 𝒎𝟐 /𝒔
- 25. b) 𝝎𝒑 = 𝒅∅ 𝒅𝒕 = 𝑴∗𝒈∗𝑫 𝑳 = 𝟑𝟎∗𝟎,𝟐𝟓 𝟏𝟖,𝟏 = 𝟎, 𝟒𝟏𝟒 𝒓𝒂𝒅/𝒔 c) 𝑻 = 𝟐∗𝝅 𝝎𝒑 = 𝟐∗𝝅 𝟎,𝟒𝟏𝟒 = 𝟏𝟓 𝒔 d) 𝑳𝑷 = 𝑰𝒄𝒎 ∗ 𝝎𝒑 = 𝑴 ∗ 𝑫𝟐 ∗ 𝝎𝒑 = 𝟑𝟎 𝟗,𝟖 ∗ 𝟎,𝟐𝟓𝟐 ∗ 𝟎, 𝟒𝟏𝟒 = 𝟎,𝟎𝟕𝟗 𝟏 𝒌𝒈 𝒎𝟐 /𝒔 La dirección es vertical, el sentido depende de L. 65. Un disco uniforme de 2,5 kg de masa y radio 6,4 cm se monta en el centro de un eje de 10 cm y gira sobre sí mismo a 700 rev/min. El eje se coloca luego en una posición horizontal con un extremo descansando sobre un pivote. Al otro extremo se le da una velocidad horizontal inicial de modo que la precesión es suave sin nutación. a) Hallar la velocidad angular de precesión. b) ¿Cuál es la velocidad del centro de masas durante la precesión? c) ¿Cuáles son el módulo y la dirección de la aceleración del centro de masas? d) ¿Cuáles son los componentes vertical y horizontal de la fuerza ejercida por el pivote? a) 𝝎𝒑 = 𝒅∅ 𝒅𝒕 = 𝑴∗𝒈∗𝑫 𝑰𝒔∗𝝎𝒔 = 𝑴∗𝒈∗𝑫 𝟏 𝟐 ∗𝑴∗𝑹𝟐∗𝝎𝒔 = 𝟐∗𝒈∗𝑫 𝑹𝟐∗𝝎𝒔 𝝎𝒑 = 𝟐∗𝟗,𝟖𝟏∗𝟎,𝟎𝟓 𝟎,𝟎𝟔𝟒𝟐∗ 𝟕𝟎𝟎𝒓𝒆𝒗 𝟏 𝒎𝒊𝒏𝒖𝒕𝒐 ∗ 𝟐 𝝅 𝒓𝒂𝒅 𝟏 𝒓𝒆𝒗 ∗ 𝟏 𝒎𝒊𝒏𝒖𝒕𝒐 𝟔𝟎 𝒔 = 𝟑, 𝟐𝟕 𝒓𝒂𝒅/𝒔 b) 𝒗𝒄𝒎 = 𝑫 ∗ 𝝎𝒑 = 𝟎, 𝟎𝟓 ∗ 𝟑, 𝟐𝟕 = 𝟎, 𝟏𝟔𝟒 𝒎/𝒔 c) 𝒂𝒄𝒎 = 𝑫 ∗ 𝝎𝒑 𝟐 = 𝟎, 𝟎𝟓 ∗ 𝟑, 𝟐𝟕𝟐 = 𝟎, 𝟓𝟑𝟓 𝒎/𝒔𝟐 d) 𝑭𝒗 = 𝑴 ∗ 𝒈 = 𝟐, 𝟓 ∗ 𝟗, 𝟖𝟏 = 𝟐𝟒, 𝟓 𝑵 𝑭𝒉 = 𝑴 ∗ 𝒂𝒄𝒎 = 𝟐, 𝟓 ∗ 𝟎, 𝟓𝟑𝟓 = 𝟏, 𝟑𝟒 𝑵 Problemas generales 66. Un objeto de masa M gira alrededor de un eje fijo con momento angular L. Su momento de inercia alrededor de este eje es I. ¿Cuál es su energía cinética? a) 𝑰𝑳𝟐 /𝟐 b) 𝑳𝟐 /𝟐𝑰 c) 𝑴𝑳𝟐 /𝟐 d) 𝑰𝑳𝟐 /𝟐𝑴 Respuesta b 67. Explicar por qué un helicóptero con un solo rotor principal posee un segundo rotor más pequeño montado en un eje horizontal en la parte trasera del aparato, como muestra la figura. Describir el movimiento resultante del helicóptero si este rotor trasero fallase durante el vuelo.
- 26. De no existir el rotor trasero la conservación de la cantidad de movimiento haría que el cuerpo del helicóptero girara en sentido contrario a las aspas superiores. 68. Una mujer se sienta sobre un taburete de piano en rotación con sus brazos cruzados. Si extiende sus brazos en cruz su energía cinética a) Crece b) Decrece c) Permanece sin variación. El momento angular se mantiene constante, en cambio el momento de Inercia se hace más grande, por tanto, la energía cinética decrece. 𝑬𝒄 = 𝑳𝟐 𝟐∗𝑰 69. En un juego de jardín, una pelota se ata a una cuerda sujeta a un poste vertical por el otro extremo. Al golpear la pelota con una paleta, la cuerda se arrolla alrededor del poste y la bola se acerca cada vez más al poste siguiendo una curva espiral. Argumentar debidamente las afirmaciones que considere correctas entre las siguientes. a) La energía mecánica y el momento angular de la bola se conservan. b) El momento angular de la vola se conserva, pero su energía mecánica crece. c) El momento angular de la bola se conserva, pero su energía mecánica disminuye. d) La energía mecánica de la bola se conserva y su momento angular crece. e) La energía mecánica de la bola se conserva y su momento angular disminuye. La pelota gira en sentido anti horario, el momento sobre la es T*R, L decrece. Respuesta e. 70. Una barra uniforme de masa M y longitud L se encuentra sobre una mesa horizontal sin rozamiento. Una porción de masilla de masa m=M/4 se mueve a lo largo de una línea perpendicular a la barra, choca contra ésta cerca de un extremo y se adhiere en el punto de contacto. Describir cualitativamente el movimiento subsiguiente de la barra y la masilla. El centro de masas de la barra masilla se moverá en línea recta, sentido y dirección de la masilla. Habrá rotación alrededor del centro de masas en el sentido de conservar L anterior del choque (mv*L/2), si imaginamos varilla horizontal y choca por el lado izquierdo, girará en sentido anti horario.
- 27. 71. Una partícula de masa 3 kg se mueve con velocidad v= 3 m/s i a lo largo de la línea z=0, y = 5,3 m. a) Determinar el momento angular L relativo al origen cuando la partícula está en el punto x= 12, y = 5,3 m. b) Una fuerza F=-3 N i se aplica a la partícula. Determinar el momento producido por estar fuerza respecto al origen. a) 𝑳 ⃗ ⃗ = 𝒓 ⃗ ⨂𝒑 ⃗ ⃗ = | 𝒊 𝒋 𝒌 ⃗ ⃗ 𝟏𝟐 𝟓, 𝟑 𝟎 𝟗 𝟎 𝟎 | = −𝟗 ∗ 𝟓, 𝟑 ∗ 𝒌 ⃗ ⃗ = −𝟒𝟕, 𝟕 𝒌 ⃗ ⃗ b) 𝝉 ⃗ = 𝒓 ⃗ ⨂𝑭 ⃗⃗ = | 𝒊 𝒋 𝒌 ⃗ ⃗ 𝟏𝟐 𝟓, 𝟑 𝟎 −𝟑 𝟎 𝟎 | = 𝟑 ∗ 𝟓, 𝟑 ∗ 𝒌 ⃗ ⃗ = −𝟏𝟓, 𝟗 𝒌 ⃗ ⃗ 72. El vector posición de una partícula de masa 3 kg viene dado por r=4 i +3 t2 j, en donde r se expresa en metros y t en segundos. Determinar el momento angular y el momento que actúa sobre la partícula respecto al origen. 𝒗 ⃗ ⃗ = 𝒅𝒓 ⃗ 𝒅𝒕 = 𝟔 ∗ 𝒕 𝒋 𝒂 ⃗ ⃗ = 𝒅𝒗 ⃗ ⃗ 𝒅𝒕 = 𝟔 𝒋 ; 𝑭 ⃗⃗ = 𝒎 ∗ 𝒂 ⃗ ⃗ = 𝟏𝟖 𝒋 𝑳 ⃗ ⃗ = 𝒓 ⃗ ⨂𝒑 ⃗ ⃗ = | 𝒊 𝒋 𝒌 ⃗ ⃗ 𝟒 𝟑 ∗ 𝒕𝟐 𝟎 𝟎 𝟏𝟖 ∗ 𝒕 𝟎 | = 𝟒 ∗ 𝟏𝟖 ∗ 𝒕 𝒌 ⃗ ⃗ = 𝟕𝟐 ∗ 𝒕 𝒌 ⃗ ⃗ 𝝉 ⃗ = 𝒓 ⃗ ⨂𝑭 ⃗⃗ = | 𝒊 𝒋 𝒌 ⃗ ⃗ 𝟒 𝟑 ∗ 𝒕𝟐 𝟎 𝟎 𝟏𝟖 𝟎 | = 𝟕𝟐 𝒌 ⃗ ⃗ 73. Una patinadora sobre hielo comienza su pirueta con los brazos extendidos girando sobre sí misma a 1,5 rev/s. Estimar su velocidad de rotación (en revoluciones por segundo) cuando ella baja los brazos verticalmente a lo largo de su cuerpo. La velocidad de rotación aumentará al disminuir el momento de inercia y conservarse el momento angular. 𝑰𝒐 ∗ 𝝎𝒐 = 𝑰𝒇 ∗ 𝝎𝒇 ; 𝝎𝒇 = 𝑰𝒐∗𝝎𝒐 𝑰𝒇 Faltan datos para hacer cálculos. 74. Dos patinadores de hielo cogidos de las manos giran en conjunto dando una revolución en 2,5 s. Sus masas son 55 kg y 85 kg y están separados 1,7 m. Determinar a) El momento angular del sistema respecto a su centro de masas. b) La energía cinética total del sistema. a) Tomando como origen del sistema de referencia la masa de 85 kg. 𝒙𝒄𝒎 = 𝒎𝟏∗𝒙𝟏+𝒎𝟐∗𝒙𝟐 𝑴 = 𝟓𝟓∗𝟏,𝟕 𝟓𝟓+𝟖𝟓 = 𝟎, 𝟔𝟔𝟖 𝒎 El momento de inercia respecto al centro de masas será:
- 28. 𝑰 = 𝒎𝟏 ∗ 𝒓𝟏 𝟐 + 𝒎𝟐 ∗ 𝒓𝟐 𝟐 = 𝟓𝟓 ∗ (𝟏,𝟕 − 𝟎, 𝟔𝟔𝟖)𝟐 + 𝟖𝟓 ∗ 𝟎,𝟔𝟔𝟖𝟐 = 𝟗𝟔,𝟓 𝒌𝒈 𝒎𝟐 𝑳 = 𝑰 ∗ 𝝎 = 𝟗𝟔,𝟓 ∗ ( 𝟐∗𝝅 𝒓𝒂𝒅 𝟐,𝟓 𝒔 ) = 𝟐𝟒𝟑 𝒌𝒈 𝒎𝟐 /𝒔 b) 𝑬𝒄 = 𝑳𝟐 𝟐 𝑰 = 𝟐𝟒𝟑𝟐 𝟐∗𝟗𝟔,𝟓 = 𝟑𝟎𝟔 𝑱 75. Una bola de 2 kg atada a una cuerda de longitud 1,5 m se mueve en una circunferencia horizontal como un péndulo cónico (figura). La cuerda forma un ángulo de ϴ=30º con la vertical. a) Demostrar que el momento angular de la bola respecto al punto de soporte P tiene un componente horizontal dirigido hacia el centro del círculo, así como un componente vertical y determinar sus valores. b) Determinar la magnitud de dL/dt y demostrar que es igual a la magnitud del momento ejercido por la gravedad respecto al punto de soporte. a) 𝑳 ⃗ ⃗ = 𝒓 ⃗ ⨂𝒑 ⃗ ⃗ En el plano x,z tenemos m.c.u.: 𝒙 = 𝒍 ∗ 𝒔𝒆𝒏𝜽 ∗ 𝒄𝒐𝒔(𝝎 ∗ 𝒕) 𝒛 = − 𝒍 ∗ 𝒄𝒐𝒔𝜽 𝒚 = 𝒍 ∗ 𝒔𝒆𝒏𝜽 ∗ 𝒔𝒆𝒏(𝝎 ∗ 𝒕) Las velocidades serán: 𝒗𝒙 = −𝒗 ∗ 𝒔𝒆𝒏(𝝎 ∗ 𝒕) 𝒗𝒚 = 𝒗 ∗ 𝒄𝒐𝒔(𝝎 ∗ 𝒕) Por dinámica calculamos las velocidades: 𝑻𝒙 = 𝑻 ∗ 𝒔𝒆𝒏𝜽 = 𝒎 ∗ 𝝎𝟐 ∗ 𝒍 ∗ 𝒔𝒆𝒏𝜽 ; 𝑻𝒚 = 𝑻 ∗ 𝒄𝒐𝒔𝜽 = 𝒎 ∗ 𝒈 𝒈 ∗ 𝒕𝒂𝒏𝜽 = 𝝎𝟐 ∗ 𝒍 ∗ 𝒔𝒆𝒏𝜽 𝝎 = √ 𝒈∗𝒕𝒂𝒏𝜽 𝒍∗𝒔𝒆𝒏𝜽 = √ 𝟗,𝟖𝟏∗𝒕𝒂𝒏𝟑𝟎 𝟏,𝟓∗𝒔𝒆𝒏𝟑𝟎 = 𝟐, 𝟕𝟓 𝒓𝒂𝒅/𝒔 𝒗 = 𝝎 ∗ 𝑹 = 𝝎 ∗ 𝒍 ∗ 𝒔𝒆𝒏𝜽 = 𝟐, 𝟕𝟓 ∗ 𝟏, 𝟓 ∗ 𝒔𝒆𝒏𝟑𝟎 = 𝟐, 𝟎𝟔 𝒎/𝒔 Con esto: 𝑳 ⃗ ⃗ = 𝒓 ⃗ ⨂𝒑 ⃗ ⃗ = 𝟐 ∗ | 𝒊 𝒋 𝒌 ⃗ ⃗ 𝒍 ∗ 𝒔𝒆𝒏𝜽 ∗ 𝒄𝒐𝒔(𝝎 ∗ 𝒕) 𝒍 ∗ 𝒔𝒆𝒏𝜽 ∗ 𝒔𝒆𝒏(𝝎 ∗ 𝒕) −𝒍 ∗ 𝒄𝒐𝒔𝜽 −𝒗 ∗ 𝒔𝒆𝒏(𝝎 ∗ 𝒕) 𝒗 ∗ 𝒄𝒐𝒔(𝝎 ∗ 𝒕) 𝟎 | 𝑳 ⃗ ⃗ = 𝟐 ∗ 𝒍 ∗ 𝒗 ∗ (𝒄𝒐𝒔𝜽 ∗ 𝒄𝒐𝒔(𝒘 ∗ 𝒕) ∗ 𝒊 + (𝒄𝒐𝒔𝜽 ∗ 𝒔𝒆𝒏(𝝎 ∗ 𝒕)) ∗ 𝒋 + 𝒔𝒆𝒏𝜽 ∗ (𝒄𝒐𝒔𝟐(𝝎 ∗ 𝒕) + 𝒔𝒆𝒏𝟐(𝝎 ∗ 𝒕)) ∗ 𝒌 ⃗ ⃗ ) 𝑳 ⃗ ⃗ = 𝟐 ∗ 𝒍 ∗ 𝒗 ∗ (𝒄𝒐𝒔𝜽 ∗ (𝒄𝒐𝒔(𝒘 ∗ 𝒕) ∗ 𝒊 + 𝒔𝒆𝒏(𝒘 ∗ 𝒕) ∗ 𝒋 + (𝒔𝒆𝒏𝜽 ∗ 𝒌 ⃗ ⃗ )
- 29. Por tanto, tenemos componente horizontal (i, j) y componente vertical(k). Poniendo valores; 𝑳 ⃗ ⃗ = 𝟔, 𝟏𝟖 ∗ (𝟎, 𝟖𝟕 ∗ (𝒄𝒐𝒔(𝒘 ∗ 𝒕) ∗ 𝒊 + 𝒔𝒆𝒏(𝒘 ∗ 𝒕)𝒋 + 𝟎, 𝟓𝒌 ⃗ ⃗ ) b) 𝒅𝑳 ⃗ ⃗ 𝒅𝒕 = 𝟐 ∗ 𝒍 ∗ 𝒗 ∗ 𝝎 ∗ 𝒄𝒐𝒔𝜽 ∗ (−𝒔𝒆𝒏(𝒘 ∗ 𝒕) ∗ 𝒊 + 𝒄𝒐𝒔(𝝎 ∗ 𝒕) ∗ 𝒋 𝒅𝑳 ⃗ ⃗ 𝒅𝒕 = 𝟔, 𝟏𝟖 ∗ 𝟎, 𝟖𝟕 ∗ 𝟐, 𝟕𝟓 ∗ (−𝒔𝒆𝒏(𝒘 ∗ 𝒕) ∗ 𝒊 + 𝒄𝒐𝒔(𝝎 ∗ 𝒕) ∗ 𝒋) En módulo: | 𝒅𝑳 ⃗ ⃗ 𝒅𝒕 | = 𝟏𝟒, 𝟕𝟐 𝑵 𝒎 Calculando el momento del peso respecto del soporte: 𝝉 = 𝒎 ∗ 𝒈 ∗ 𝒓 ∗ 𝒔𝒆𝒏𝜽 = 𝟐 ∗ 𝟗, 𝟖 ∗ 𝟏, 𝟓 ∗ 𝒔𝒆𝒏𝟑𝟎 = 𝟏𝟒, 𝟕 𝑵 𝒎 76. Una masa m situada sobre una superficie horizontal sin rozamiento está sujeta a una cuerda que se arrolla alrededor de un poste cilíndrico vertical, de modo que cuando se pone en movimiento sigue una trayectoria en espiral hacia dentro. a) ¿Se conserva el momento angular de la masa? b) ¿Se conserva la energía de la masa? c) Si la velocidad de la masa es vo cuando la longitud de la cuerda el r, ¿Cuál será su velocidad cuando la longitud de la cuerda no arrollada sea r/2? a) El momento es R*T, L decrece b) La energía cinética se mantiene constante en ausencia de fricción. c) 𝑬𝒄 = 𝟏 𝟐 ∗ 𝑰 ∗ 𝝎𝟐 = 𝟏 𝟐 ∗ 𝒎 ∗ 𝒓𝟐 ∗ 𝒗𝟐 𝒓𝟐 = 𝟏 𝟐 ∗ 𝒎 ∗ 𝒗𝟐 La energía se mantiene constante y la velocidad también. 77. La figura muestra un tubo cilíndrico hueco de masa M, longitud L y momento de inercia ML2 /10. Dentro del cilindro se encuentran dos masas m separadas una distancia l y atadas a un vástago central por una delgada cuerda. El sistema puede girar alrededor de un eje vertical a través de un cilindro. Cuando el sistema gira con velocidad angular ω, las cuerdas que mantienen las masas se rompen súbitamente. Obtener las expresiones correspondientes a la velocidad angular final y a las energías inicial y final del sistema. Suponer que las paredes interiores del cilindro carecen de rozamiento.
- 30. Al ser un sistema aislado se conserva la cantidad de movimiento. 𝑳𝒊 = 𝑳𝒇 𝑰𝒊 ∗ 𝝎𝒊 = 𝑰𝒇 ∗ 𝝎𝒇 𝝎𝒇 = 𝑰𝒊∗𝝎𝒊 𝑰𝒇 Las expresiones de los momentos de inercia son: 𝑰𝒊 = 𝑴∗𝑳𝟐 𝟏𝟎 + 𝟐 ∗ 𝒎 ∗ 𝒍𝟐 𝟒 𝑰𝒇 = 𝑴∗𝑳𝟐 𝟏𝟎 + 𝟐 ∗ 𝒎 ∗ 𝑳𝟐 𝟒 Por tanto: 𝝎𝒇 = 𝑴∗𝑳𝟐 𝟏𝟎 +𝟐∗𝒎∗ 𝒍𝟐 𝟒 𝑴∗𝑳𝟐 𝟏𝟎 +𝟐∗𝒎∗ 𝑳𝟐 𝟒 ∗ 𝝎 = 𝑴+𝟓∗𝒎∗ 𝒍𝟐 𝑳𝟐 𝑴+𝟓∗𝒎 ∗ 𝝎 = 𝑴∗𝑳𝟐+𝟓∗𝒎∗𝒍𝟐 𝑴∗𝑳𝟐+𝟓∗𝒎∗𝑳𝟐 Para las energías: 𝑬𝒄,𝒊 = 𝟏 𝟐 ∗ 𝑰𝒊 ∗ 𝝎𝒊 𝟐 = 𝟏 𝟐 ∗ ( 𝑴∗𝑳𝟐 𝟏𝟎 + 𝟐 ∗ 𝒎 ∗ 𝒍𝟐 𝟒 ) ∗ 𝝎𝟐 = 𝟏 𝟒 ∗ ( 𝑴∗𝑳𝟐 𝟓 + 𝒎 ∗ 𝒍𝟐 ) ∗ 𝝎𝟐 𝑬𝒄,𝒊 = 𝟏 𝟐𝟎 ∗ (𝑴 ∗ 𝑳𝟐 + 𝟓 ∗ 𝒎 ∗ 𝒍𝟐) ∗ 𝝎𝟐 𝑬𝒄,𝒇 = 𝟏 𝟐 ∗ 𝑰𝒇 ∗ 𝝎𝒇 𝟐 = 𝟏 𝟐 ∗ ( 𝑴∗𝑳𝟐 𝟏𝟎 + 𝟐 ∗ 𝒎 ∗ 𝑳𝟐 𝟒 ) ∗ ( 𝑴+𝟓∗𝒎∗ 𝒍𝟐 𝑳𝟐 𝑴+𝟓∗𝒎 ∗ 𝝎) 𝟐 𝑬𝒄,𝒇 = 𝟏 𝟐𝟎 ∗ (𝑴 ∗ 𝑳𝟐 + 𝟓 ∗ 𝒎 ∗ 𝑳𝟐) ∗ (𝑴∗𝑳𝟐+𝟓∗𝒎∗𝒍𝟐) 𝟐 (𝑴∗𝑳𝟐+𝟓∗𝒎∗𝑳𝟐) 𝟐 ∗ 𝝎𝟐 𝑬𝒄,𝒇 = 𝟏 𝟐𝟎 ∗ (𝑴∗𝑳𝟐+𝟓∗𝒎∗𝒍𝟐) 𝟐 𝑴∗𝑳𝟐+𝟓∗𝒎∗𝑳𝟐 ∗ 𝝎𝟐 78. Repetir el problema 77 suponiendo ahora que existe rozamiento entre las masas y las paredes del cilindro. Sin embargo, el coeficiente de rozamiento no es suficiente para evitar que las masas alcancen los extremos del cilindro. ¿Puede determinarse la energía final del sistema sin coeficiente de rozamiento cinético? No existen fuerzas externas actuando, el momento total se conserva. La situación inicial y final del problema son las mismas que en el problema anterior y los resultados también. 79. Supongamos que en la figura del problema 77 l=0,6 m, L=2,0 m, M=0,8 kg y m=0,4 kg. El sistema gira con la velocidad angular ω, de tal modo que la tensión en la cuerda es 108 N justo antes de que se rompa. Determinar las
- 31. velocidades angulares inicial y final, así como las energías inicial y final del sistema. Suponer que las paredes interiores del cilindro carecen de rozamiento. Para encontrar la velocidad angular inicial: 𝑻 = 𝒎 ∗ 𝝎𝟐 ∗ 𝒍 𝟐 𝝎 = √ 𝟐∗𝑻 𝒎∗𝒍 = √ 𝟐∗𝟏𝟎𝟖 𝟎,𝟒∗𝟎,𝟔 = 𝟑𝟎, 𝟎 𝒓𝒂𝒅/𝒔 Utilizando las ecuaciones del problema 77: 𝝎𝒇 = 𝑴+𝟓∗𝒎∗ 𝒍𝟐 𝑳𝟐 𝑴+𝟓∗𝒎 ∗ 𝝎 = 𝟎,𝟖+𝟓∗𝟎,𝟒∗ 𝟎,𝟔𝟐 𝟐𝟐 𝟎,𝟖+𝟓∗𝟎,𝟒 ∗ 𝟑𝟎 = 𝟏𝟎, 𝟓 𝒓𝒂𝒅/𝒔 80. Determinar en el problema 77 la velocidad final de cada masa justo antes de que alcance el extremo del cilindro. La energía del sistema se ha de conservar entre la situación final y la inicial. En la situación final tenemos la velocidad de rotación y la velocidad radial de desplazamiento de las masas. 𝟏 𝟐 ∗ 𝑰𝒊 ∗ 𝝎𝒊 𝟐 = 𝟏 𝟐 ∗ 𝑰𝒇 ∗ 𝝎𝒇 𝟐 + 𝟏 𝟐 ∗ 𝟐 ∗ 𝒎 ∗ 𝒗𝒓 𝟐 𝒗𝒓 = √ 𝟏 𝟐 ∗𝑰𝒊∗𝝎𝒊 𝟐− 𝟏 𝟐 ∗𝑰𝒇∗𝝎𝒇 𝟐 𝒎 Utilizando las expresiones del problema 77: 𝒗𝒓 = √ 𝟏 𝟐𝟎 ∗ (𝑴 ∗ 𝑳𝟐 + 𝟓 ∗ 𝒎 ∗ 𝒍𝟐) ∗ 𝝎𝟐 − 𝟏 𝟐𝟎 ∗ (𝑴 ∗ 𝑳𝟐 + 𝟓 ∗ 𝒎 ∗ 𝒍𝟐)𝟐 𝑴 ∗ 𝑳𝟐 + 𝟓 ∗ 𝒎 ∗ 𝑳𝟐 ∗ 𝝎𝟐 𝒎 81. Con los datos numéricos del problema 79, suponer que el coeficiente de rozamiento entre las masas y las paredes del cilindro es tal que las masas dejan de deslizarse 0,2 m antes de alcanzar los extremos del cilindro. Determinar las velocidades angulares final y inicial del sistema y la energía disipada por rozamiento. 𝑻 = 𝒎 ∗ 𝝎𝟐 ∗ 𝒍 𝟐 𝝎𝒊 = √ 𝟐∗𝑻 𝒎∗𝒍 = √ 𝟐∗𝟏𝟎𝟖 𝟎,𝟒∗𝟎,𝟔 = 𝟑𝟎, 𝟎 𝒓𝒂𝒅/𝒔 𝑳𝒊 = 𝑳𝒇 𝑰𝒊 ∗ 𝝎𝒊 = 𝑰𝒇 ∗ 𝝎𝒇 𝝎𝒇 = 𝑰𝒊∗𝝎𝒊 𝑰𝒇 𝑰𝒊 = 𝑴∗𝑳𝟐 𝟏𝟎 + 𝟐 ∗ 𝒎 ∗ 𝒍𝟐 𝟒 𝑰𝒇 = 𝑴∗𝑳𝟐 𝟏𝟎 + 𝟐 ∗ 𝒎 ∗ 𝑳′𝟐 𝟒 Por tanto: 𝝎𝒇 = 𝑴∗𝑳𝟐 𝟏𝟎 +𝟐∗𝒎∗ 𝒍𝟐 𝟒 𝑴∗𝑳𝟐 𝟏𝟎 +𝟐∗𝒎∗ 𝑳′𝟐 𝟒 ∗ 𝝎 = 𝑴∗𝑳𝟐+𝟓∗𝒎∗𝒍𝟐 𝑴∗𝑳𝟐+𝟓∗𝒎∗𝑳′𝟐 ∗ 𝝎 = 𝟎,𝟖∗𝟐𝟐+𝟓∗𝟎,𝟒∗𝟎,𝟔𝟐 𝟎,𝟖∗𝟐𝟐+𝟓∗𝟎,𝟒∗𝟏,𝟔𝟐 ∗ 𝟑𝟎 = 𝟏𝟒,𝟏 𝒓𝒂𝒅/𝒔
- 32. 𝑬𝒄,𝒊 = 𝟏 𝟐𝟎 ∗ (𝑴 ∗ 𝑳𝟐 + 𝟓 ∗ 𝒎 ∗ 𝒍𝟐) ∗ 𝝎𝟐 = 𝟏 𝟐𝟎 ∗ (𝟎, 𝟖 ∗ 𝟐𝟐 + 𝟓 ∗ 𝟎, 𝟒 ∗ 𝟎, 𝟔𝟐) ∗ 𝟑𝟎𝟐 = 𝟏𝟕𝟔, 𝟒 𝑱 𝑬𝒄,𝒇 = 𝟏 𝟐 ∗ 𝑰𝒇 ∗ 𝝎𝒇 𝟐 = 𝟏 𝟐 ∗ ( 𝑴∗𝑳𝟐 𝟏𝟎 + 𝟐 ∗ 𝒎 ∗ 𝑳′𝟐 𝟒 ) ∗ 𝝎𝒇 𝟐 = 𝟏 𝟐 ∗ ( 𝟎,𝟖∗𝟐𝟐 𝟏𝟎 + 𝟐 ∗ 𝟎, 𝟒 ∗ 𝟏,𝟔𝟐 𝟒 ) ∗ 𝟏𝟒, 𝟏𝟐 = 𝟖𝟐, 𝟕 𝑱 ∆𝑬 = 𝟖𝟐, 𝟕 − 𝟏𝟕𝟔, 𝟒 = −𝟗𝟑, 𝟕 𝑱 82. La segunda ley de Newton establece que el radio vector del Sol a un planeta barre áreas iguales en tiempos iguales. Demostrar que esta ley resulta directamente del principio de conservación del momento angular, teniendo en cuenta, además, que la fuerza de atracción gravitatoria entre un planeta y el Sol actúa a lo largo de la línea que une a los dos objetos celestes. 𝒅𝑨 𝒅𝒕 = 𝟏 𝟐 ∗ 𝒓𝟐 ∗ 𝒅𝜽 𝒅𝒕 = 𝟏 𝟐 ∗ 𝒓𝟐 ∗ 𝝎 Dado que la fuerza gravitatoria es central L es constante. 𝑳 = 𝒎 ∗ 𝒓𝟐 ∗ 𝝎 De las dos ecuaciones: 𝒅𝑨 𝒅𝒕 = 𝑳 𝟐∗𝒎 = 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕𝒆 83. La figura muestra un cilindro hueco de longitud 1,8 m, masa 0,8 kg y radio 0,2 m que puede girar libremente alrededor de un eje vertical que pasa por su centro y es perpendicular al eje del cilindro. Dentro del cilindro hay dos discos delgados de masa 0,2 kg conectados a sendos muelles de constante de fuerza k=25 N/m y longitudes naturales 0,4 m. El sistema alcanza una velocidad de rotación de 8 rad/s con los muelles bloqueados de modo que no pueden alargarse. Los muelles se desbloquean entonces súbitamente. Debido al rozamiento que experimentan sobre la pared interna del cilindro, los discos se detienen a una distancia 0,6 m del eje central. ¿Cuál será entonces la velocidad angular del cilindro? ¿Cuánta energía cinética se disipa en el rozamiento entre los discos y la pared del cilindro?
- 33. 𝑳𝒊 = 𝑳𝒇 𝑰𝒊 ∗ 𝝎𝒊 = 𝑰𝒇 ∗ 𝝎𝒇 𝝎𝒇 = 𝑰𝒊∗𝝎𝒊 𝑰𝒇 Para los momentos de inercia tenemos, un cilindro hueco y dos masas con forma de disco: 𝑰𝒊 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ 𝑹𝟐 + 𝟐 ∗ ( 𝟏 𝟒 ∗ 𝒎 ∗ 𝒓𝟐 + 𝒎 ∗ 𝒍𝟐 ) 𝑰𝒊 = 𝟏 𝟏𝟐 ∗ 𝟎, 𝟖 ∗ 𝟏, 𝟖𝟐 + 𝟏 𝟐 ∗ 𝟎, 𝟖 ∗ 𝟎, 𝟐𝟐 + 𝟐 ∗ ( 𝟏 𝟒 ∗ 𝟎, 𝟐 ∗ 𝟎, 𝟐𝟐 + 𝟎, 𝟐 ∗ 𝟎, 𝟒𝟐 ) 𝑰𝒊 = 𝟎, 𝟑𝟎 𝒌𝒈 𝒎𝟐 Para la situación final: 𝑰𝒇 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ 𝑹𝟐 + 𝟐 ∗ ( 𝟏 𝟒 ∗ 𝒎 ∗ 𝒓𝟐 + 𝒎 ∗ 𝒍𝟐 ) 𝑰𝒇 = 𝟏 𝟏𝟐 ∗ 𝟎. 𝟖 ∗ 𝟏. 𝟖𝟐 + 𝟏 𝟐 ∗ 𝟎. 𝟖 ∗ 𝟎. 𝟐𝟐 + 𝟐 ∗ ( 𝟏 𝟒 ∗ 𝟎. 𝟐 ∗ 𝟎. 𝟐𝟐 + 𝟎. 𝟐 ∗ 𝟎. 𝟔𝟐 ) 𝑰𝒇 = 𝟎, 𝟑𝟖 𝒌𝒈 𝒎𝟐 Con esto: 𝝎𝒇 = 𝟎,𝟑𝟎∗𝟖 𝟎,𝟑𝟖 = 𝟔, 𝟑𝟐 𝒓𝒂𝒅/𝒔 La energía final es potencial elástica y cinética, la inicial es cinética: 𝑬𝒄,𝒊 = 𝟏 𝟐 ∗ 𝑰𝒊 ∗ 𝝎𝒊 𝟐 = 𝟏 𝟐 ∗ 𝟎, 𝟑 ∗ 𝟖𝟐 = 𝟗, 𝟔 𝑱 𝑬𝒄,𝒇 = 𝟏 𝟐 ∗ 𝑰𝒇 ∗ 𝝎𝒇 𝟐 + 𝟏 𝟐 ∗ 𝒌 ∗ 𝒙𝟐 = 𝟏 𝟐 ∗ 𝟎, 𝟑𝟖 ∗ 𝟔, 𝟑𝟐𝟐 + 𝟏 𝟐 ∗ 𝟐𝟓 ∗ 𝟎, 𝟐𝟐 𝑬𝒄,𝒇 = 𝟖, 𝟗 𝑱 ∆𝑬𝒄 = 𝟖, 𝟗 − 𝟗, 𝟔 = −𝟏, 𝟓 𝑱 84. a) Suponiendo que la Tierra es una esfera homogénea de radio r y masa m, demostrar que el período de la rotación terrestre alrededor de su eje está relacionado con el radio 𝑻 = ( 𝟒𝝅𝒎 𝟓𝑳 )𝒓𝟐 , en donde L es el momento angular de la Tierra debido a su rotación. b)Suponer que el radio r cambia en una cantidad muy pequeña debido a algún efecto interno, tal como la dilatación térmica. Demostrar que el cambio fraccional en el período ∆T viene dado aproximadamente por ∆𝑻 𝑻 = 𝟐∆𝒓/𝒓. Sugerencia: Utilizar las diferenciales dr y dT como aproximaciones de estas magnitudes. c) ¿Cuántos kilómetros necesitaría la Tierra expansionarse para que el período cambiase ¼ día/año, de modo que los años bisiestos no fueran necesarios? a) 𝑳 = 𝑰 ∗ 𝝎 𝑳 = 𝟐 𝟓 ∗ 𝒎 ∗ 𝒓𝟐 ∗ 𝝎 ; 𝝎 = 𝟓∗𝑳 𝟐∗𝒎∗𝒓𝟐 𝝎 = 𝟐∗𝝅 𝑻 ; 𝑻 = 𝟐∗𝝅 𝝎 = 𝟐∗𝝅 𝟓∗𝑳 𝟐∗𝒎∗𝒓𝟐 = 𝟒∗𝝅∗𝒎∗𝒓𝟐 𝟓∗𝑳 b) 𝒅𝑻 𝒅𝒓 = 𝟖∗𝝅∗𝒎∗𝒓 𝟓∗𝑳 = 𝟐 ∗ 𝟒∗𝝅∗𝒎 𝟓∗𝑳 ∗ 𝒓 = 𝟐 ∗ 𝑻 𝒓𝟐 ∗ 𝒓 = 𝟐 ∗ 𝑻 𝒓 Despejamos dT/T:
- 34. 𝒅𝑻 𝑻 = 𝟐∗𝒅𝒓 𝒓 en incrementos: ∆𝑻 𝑻 = 𝟐 ∗ ∆𝒓 𝒓 c) ∆𝑻 𝑻 = 𝟏 𝟒 𝒅𝒊𝒂 𝟏 𝒂ñ𝒐 ∗ 𝟏 𝒂ñ𝒐 𝟑𝟔𝟓,𝟐𝟒 𝒅𝒊𝒂𝒔 = 𝟐 ∗ ∆𝒓 𝟔,𝟑𝟕 𝟏𝟎𝟑𝒌𝒎 ∆𝒓 = 𝟔,𝟑𝟕∗𝟏𝟎𝟑 𝟒∗𝟑𝟔𝟓,𝟐𝟒∗𝟐 = 𝟐, 𝟏𝟖 𝒌𝒎 85. Los casquetes polares de la Tierra contienen aproximadamente 2,3 1019 kg de hielo. Su masa contribuye muy poco al momento de inercia de la Tierra, ya que está localizada en los polos, próxima al eje de rotación. Estimar el cambio de duración del día que tendría lugar si los casquetes polares se fundieran y el agua resultante se distribuyera uniformemente por toda la superficie de la Tierra. (El momento de inercia de una corteza esférica de masa m y radio r es 2/3mr2 ). 𝑳 = 𝑰 ∗ 𝝎 ;𝝎 = 𝑳/𝑰 𝑻 = 𝟐∗𝝅 𝒘 = 𝟐∗𝝅∗𝑰 𝑳 𝒅𝑻 𝒅𝑰 = 𝟐∗𝝅 𝑳 = 𝑻 𝑰 𝒅𝑻 𝑻 = 𝒅𝑰 𝑰 , en incrementos: ∆𝑻 𝑻 = ∆𝑰 𝑰 ∆𝑻 = 𝑻 ∗ ∆𝑰 𝑰 ∆𝑻 = 𝟐𝟒 𝒉𝒐𝒓𝒂𝒔 ∗ 𝟑𝟔𝟎𝟎 𝒔 ∗𝟏 𝒉𝒐𝒓𝒂 ∗ 𝟐 𝟑 ∗𝒎∗𝒓𝟐 𝟐 𝟓 ∗𝑴∗𝒓𝟐 ∆𝑻 = 𝟐𝟒 ∗ 𝟑𝟔𝟎𝟎 ∗ 𝟓∗𝟐,𝟑 𝟏𝟎𝟏𝟗 𝟑∗𝟔 𝟏𝟎𝟐𝟒 = 𝟎, 𝟓𝟓𝟐 𝒔 86. La figura muestra un cilindro hueco de masa M=1,2 kg y longitud L=1,6 m que puede girar libremente alrededor de un eje vertical que pasa por su centro. En su interior hay dos discos, cada uno de masa 0,4 kg que están atados a un vástago central por una cuerda delgada y separados por una distancia l=0,8 m. La cuerda se rompe si la tensión excede 100 N. Partiendo del reposo se aplica un momento al sistema hasta que la cuerda se rompe. (Se supone que los discos son puntuales y el radio del cilindro depreciable). Determinar el trabajo realizado hasta ese instante. En ese momento deja de aplicarse el momento y se supone que las paredes del cilindro carecen de rozamiento. Obtener una expresión para la velocidad angular del sistema en función de x para 𝒙 < 𝑳/𝟐, siendo x la distancia entre cada disco y el vástago central. Aplicamos la segunda ley de Newton:
- 35. 𝑻 = 𝒎 ∗ 𝝎𝟐 ∗ 𝒓 ; 𝝎 = √ 𝑻 𝒎∗𝒓 = √ 𝟏𝟎𝟎 𝟎,𝟒∗𝟎,𝟒 = 𝟐𝟓, 𝟎 𝒓𝒂𝒅/𝒔 El momento de inercia inicial, en el momento de la rotura: 𝑰𝒊 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝟐 ∗ 𝒎 ∗ ( 𝒍 𝟐 ) 𝟐 𝑰𝒊 = 𝟏 𝟏𝟐 ∗ 𝟏, 𝟐 ∗ 𝟏, 𝟔𝟐 + 𝟐 ∗ 𝟎, 𝟒 ∗ ( 𝟎,𝟖 𝟐 ) 𝟐 = 𝟎, 𝟑𝟖𝟒 𝒌𝒈 𝒎𝟐 Para el momento de inercia en función de x: 𝑰 = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝟐 ∗ 𝒎 ∗ 𝒙𝟐 = 𝟎, 𝟐𝟓𝟔 + 𝟎, 𝟖 ∗ 𝒙𝟐 La energía inicial: 𝑬𝒄 = 𝟏 𝟐 ∗ 𝑰𝒊 ∗ 𝝎𝒊 𝟐 = 𝟏 𝟐 ∗ 𝟎, 𝟑𝟖𝟒 ∗ 𝟐𝟓𝟐 = 𝟏𝟐𝟎 𝑱 = 𝑾 Para la expresión de la velocidad en función de x aplicamos la conservación del momento angular: 𝑰𝒊 ∗ 𝝎𝒊 = 𝑰𝒙 ∗ 𝝎𝒙 𝝎𝒙 = 𝑰𝒊∗𝝎𝒊 𝑰𝒙 = 𝟎.𝟑𝟖𝟒∗𝟐𝟓 𝟎,𝟐𝟓𝟔+𝟎,𝟖∗𝒙𝟐 = 𝟗,𝟔 𝟎,𝟐𝟓𝟔+𝟎,𝟖∗𝒙𝟐 87. Determinar en el problema 86 la velocidad angular del sistema justamente antes y después que los discos pasen por los extremos del cilindro. Utilizamos la expresión del problema anterior: 𝝎𝟎,𝟖 = 𝟗,𝟔 𝟎,𝟐𝟓𝟔∗𝟎,𝟖∗𝟎,𝟖𝟐 = 𝟏𝟐, 𝟓 𝒓𝒂𝒅/𝒔 La velocidad es la misma en los dos casos. 88. Repetir el problema 86 con el radio del cilindro hueco igual a 0,4 m y las masas tratadas como discos delgados en lugar de masas puntuales. El momento de inercia en este caso será: 𝑰(𝒙) = 𝑰𝒄𝒊𝒍 + 𝟐 ∗ 𝑰𝒎 𝑰(𝒙) = 𝟏 𝟏𝟐 ∗ 𝑴 ∗ 𝑳𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ 𝑹𝟐 + 𝟐 ∗ ( 𝟏 𝟒 ∗ 𝒎 ∗ 𝑹𝟐 + 𝒎 ∗ 𝒙𝟐 ) 𝑰(𝟎, 𝟒) = 𝟏 𝟏𝟐 ∗ 𝟏, 𝟐 ∗ 𝟏. 𝟔𝟐 + 𝟏 𝟐 ∗ 𝟏, 𝟐 ∗ 𝟎, 𝟒𝟐 + 𝟐 ∗ 𝟎, 𝟒 ∗ ( 𝟏 𝟒 ∗ 𝟎, 𝟒𝟐 + 𝟎, 𝟒𝟐) = 𝟎, 𝟑𝟖𝟒 + 𝟎, 𝟖 ∗ 𝟎, 𝟒𝟐 = 𝟎, 𝟓𝟏𝟐 𝒌𝒈 𝒎𝟐 𝑻 = 𝒎 ∗ 𝝎𝟐 ∗ 𝒓 ; 𝝎 = √ 𝑻 𝒎∗𝒓 = √ 𝟏𝟎𝟎 𝟎,𝟒∗𝟎,𝟒 = 𝟐𝟓, 𝟎 𝒓𝒂𝒅/𝒔 𝑬𝒄 = 𝟏 𝟐 ∗ 𝑰𝒊 ∗ 𝝎𝒊 𝟐 = 𝟏 𝟐 ∗ 𝟎, 𝟓𝟏𝟐 ∗ 𝟐𝟓𝟐 = 𝟏𝟔𝟎 𝑱 = 𝑾 𝑰𝒊 ∗ 𝝎𝒊 = 𝑰𝒙 ∗ 𝝎𝒙 𝝎𝒙 = 𝑰𝒊∗𝝎𝒊 𝑰𝒙 = 𝟎.𝟓𝟏𝟐∗𝟐𝟓 𝟎,𝟑𝟖𝟒+𝟎,𝟖∗𝒙𝟐 = 𝟏𝟐,𝟖 𝟎,𝟑𝟖𝟒+𝟎,𝟖∗𝒙𝟐 89. La figura muestra una polea formada por un disco uniforme, del cual pende una cuerda pesada. La circunferencia de la polea es de 1,2 m y su masa de 2,2 kg. La cuerda tiene 8,0 m de longitud y su masa es 4,8 kg. En el instante mostrado en la figura, el sistema está en reposo y la diferencia de altura de los dos extremos de la cuerda es 0,6 m. a) ¿Cuál es la velocidad angular de la polea cuando la diferencia de altura entre los extremos de la cuerda es de 7,2 m?
- 36. b) Obtener una expresión para el momento angular del sistema en función del tiempo, prescindiendo del caso en que cualquiera de los extremos de la cuerda está por encima del centro de la polea. No hay deslizamiento entre la cuerda y la polea. a) El radio de la polea 𝑹 = 𝑳 𝟐∗𝝅 = 𝟏,𝟐 𝟐∗𝝅 = 𝟎, 𝟏𝟗𝟏 𝒎 Para calcular la longitud de la cuerda que hay a cada lado de la polea: El subíndice 1 es la parte de la izquierda y el dos la derecha. 𝒍𝟐𝒊 − 𝒍𝟏𝒊 = 𝟎, 𝟔 Como la cuerda tiene 8 m y la diferencia de alturas es de 0,6 m: 𝒍𝟐𝒊 + 𝒍𝟏𝒊 = 𝟕, 𝟒 De las dos ecuaciones tenemos: 𝒍𝟏𝒊 = 𝟑, 𝟒 𝒎 ; 𝒍𝟐𝒊 = 𝟒 𝒎 Para la situación final: 𝒍𝟐𝒇 − 𝒍𝟏𝒇 = 𝟕, 𝟐 𝒍𝟐𝒇 + 𝒍𝟏𝒇 = 𝟕, 𝟒 𝒍𝟐𝒇 = 𝟕, 𝟑 𝒎 ; 𝒍𝟏𝒇 = 𝟎, 𝟏 𝒎 La masa de la cuerda será: 𝒎 = 𝝀 ∗ 𝑳 ; 𝝀 = 𝒎 𝑳 = 𝟒,𝟖 𝟖 = 𝟎, 𝟔 𝒌𝒈/𝒎 El origen de energía potencial lo cogemos en el centro de la polea, el centro de masas de cada parte de la cuerda está en su parte media(L/2). La energía potencial inicial: 𝑬𝒑𝒊 = − 𝟏 𝟐 ∗ (𝑳𝟏𝒊 ∗ 𝝀) ∗ 𝒈 ∗ 𝑳𝟏𝒊 − 𝟏 𝟐 ∗ (𝑳𝟐𝒊 ∗ 𝝀) ∗ 𝒈 ∗ 𝑳𝟐𝒊 = − 𝟏 𝟐 ∗ 𝒈 ∗ 𝝀 ∗ (𝑳𝟏𝒊 𝟐 + 𝑳𝟐𝒊 𝟐 ) Para la final: 𝑬𝒑𝒇 = − 𝟏 𝟐 ∗ (𝑳𝟏𝒇 ∗ 𝝀) ∗ 𝒈 ∗ 𝑳𝟏𝒇 − 𝟏 𝟐 ∗ (𝑳𝟐𝒇 ∗ 𝝀) ∗ 𝒈 ∗ 𝑳𝟐𝒇 = − 𝟏 𝟐 ∗ 𝒈 ∗ 𝝀 ∗ (𝑳𝟏𝒇 𝟐 + 𝑳𝟐𝒇 𝟐 ) Teniendo en cuenta la conservación de la energía: 𝑬𝒄𝒇 = −𝚫𝑬𝒑 = 𝑬𝒑𝒊 − 𝑬𝒑𝒇 = 𝟏 𝟐 ∗ 𝒈 ∗ 𝝀 ∗ (−𝑳𝟏𝒊 𝟐 − 𝑳𝟐𝒊 𝟐 + 𝑳𝟏𝒇 𝟐 + 𝑳𝟐𝒇 𝟐 ) 𝑬𝒄𝒇 = 𝟏 𝟐 ∗ 𝟗, 𝟖𝟏 ∗ 𝟎, 𝟔 ∗ (−𝟑, 𝟒𝟐 − 𝟒𝟐 + 𝟕, 𝟑𝟐 + 𝟎, 𝟏𝟐) = 𝟕𝟓, 𝟕𝟓 𝑱 La energía cinética será: 𝑬𝒄 = 𝟏 𝟐 ∗ 𝑰 ∗ 𝝎𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ 𝒗𝟐 = 𝟏 𝟐 ∗ ( 𝟏 𝟐 ∗ 𝑴𝒑 ∗ 𝑹𝟐 ) ∗ 𝝎𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ 𝝎𝟐 ∗ 𝑹𝟐 𝝎 = 𝟏 𝑹 ∗ √ 𝑬𝒄 𝟏 𝟒 ∗𝑴𝒑+ 𝟏 𝟐 ∗𝑴 = 𝟏 𝟎,𝟏𝟗𝟏 ∗ √ 𝟕𝟓,𝟕𝟓 𝟏 𝟒 ∗𝟐,𝟐+ 𝟏 𝟐 ∗𝟒,𝟖 = 𝟐𝟔, 𝟓 𝒓𝒂𝒅/𝒔
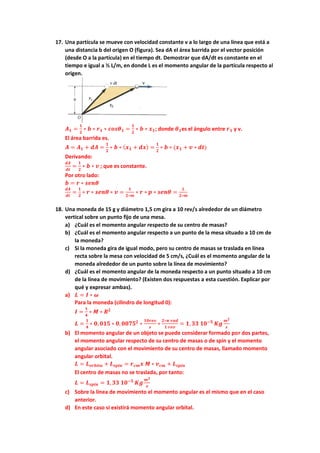
- 37. b) 𝑳 = 𝑳𝒑 + 𝑳𝒄 = 𝑰𝒑 ∗ 𝝎 + 𝑴𝒄 ∗ 𝑹𝟐 ∗ 𝝎 = 𝟏 𝟐 ∗ 𝑴𝒑 ∗ 𝑹𝟐 ∗ 𝝎 + 𝑴𝒄 ∗ 𝑹𝟐 ∗ 𝝎 𝑳 = 𝑹𝟐 ∗ 𝝎 ∗ ( 𝟏 𝟐 ∗ 𝑴𝒑 + 𝑴𝒄) Pondremos la energía potencial en función del ángulo girado por la polea ϴ: 𝑼(𝜽) = − 𝟏 𝟐 ∗ 𝒈 ∗ 𝝀 ∗ [(𝒍𝟏𝒊 − 𝑹 ∗ 𝜽)𝟐] + (𝒍𝟐𝒊 − 𝑹 ∗ 𝜽)𝟐 𝚫𝑼 = 𝑼(𝜽) − 𝑼(𝟎) 𝚫𝑼 = − 𝟏 𝟐 ∗ 𝒈 ∗ 𝝀 ∗ [(𝒍𝟏𝒊 − 𝑹 ∗ 𝜽)𝟐 + (𝒍𝟐𝒊 − 𝑹 ∗ 𝜽)𝟐] + 𝟏 𝟐 ∗ 𝒈 ∗ 𝝀 ∗ [(𝒍𝟏𝒊)𝟐 + (𝒍𝟐𝒊)𝟐] 𝚫𝐔 = −𝑹𝟐 ∗ 𝝀 ∗ 𝜽𝟐 ∗ 𝒈 + (𝒍𝟏𝒊 − 𝒍𝟐𝒊) ∗ 𝑹 ∗ 𝜽 ∗ 𝝀 ∗ 𝒈 Para el t=0 las dos ramas de la cuerda igualadas, l1i=l2i. 𝚫𝑼 = −𝑹𝟐 ∗ 𝝀 ∗ 𝜽𝟐 ∗ 𝒈 Aplicando 𝑬𝒄 = −𝚫𝐔 = 𝑹𝟐 ∗ 𝝀 ∗ 𝜽𝟐 ∗ 𝒈 𝟏 𝟐 ∗ ( 𝟏 𝟐 ∗ 𝑴𝒑 ∗ 𝑹𝟐 ) ∗ 𝝎𝟐 + 𝟏 𝟐 ∗ 𝑴 ∗ 𝝎𝟐 ∗ 𝑹𝟐 = 𝑹𝟐 ∗ 𝝀 ∗ 𝜽𝟐 ∗ 𝒈 𝝎 = 𝜽 ∗ √ 𝝀∗𝒈 𝟏 𝟒 ∗𝑴𝒑+ 𝟏 𝟐 ∗𝑴 = 𝜽 ∗ √ 𝟎.𝟔∗𝟗.𝟖𝟏 𝟏 𝟒 ∗𝟐,𝟐+ 𝟏 𝟐 ∗𝟒,𝟖 = 𝟏, 𝟒𝟏 ∗ 𝜽 Teniendo en cuenta 𝝎 = 𝒅𝜽 𝒅𝒕 𝒅𝜽 𝒅𝒕 = 𝟏, 𝟒𝟏 ∗ 𝜽 Integrando: 𝒍𝒏𝜽 = 𝟏, 𝟒𝟏 ∗ 𝒕 𝜽 = 𝒆𝟏,𝟒𝟏∗𝒕 Derivando: 𝝎 = 𝟏, 𝟒𝟏 ∗ 𝒆𝟏,𝟒𝟏∗𝒕 Usando la expresión de L: 𝑳 = 𝑹𝟐 ∗ 𝝎 ∗ ( 𝟏 𝟐 ∗ 𝑴𝒑 + 𝑴𝒄) = 𝑳 = 𝑹𝟐 ∗ 𝟏,𝟒𝟏 ∗ 𝒆𝟏,𝟒𝟏∗𝒕 ∗ ( 𝟏 𝟐 ∗ 𝑴𝒑 + 𝑴𝒄) 𝑳 = 𝟎, 𝟏𝟗𝟏𝟐 ∗ 𝟏, 𝟒𝟏 ∗ 𝒆𝟏,𝟒𝟏∗𝒕 ∗ ( 𝟏 𝟐 ∗ 𝟐, 𝟐 + 𝟒, 𝟖) = 𝟎, 𝟑𝟎𝟑 ∗ 𝒆𝟏,𝟒𝟏∗𝒕