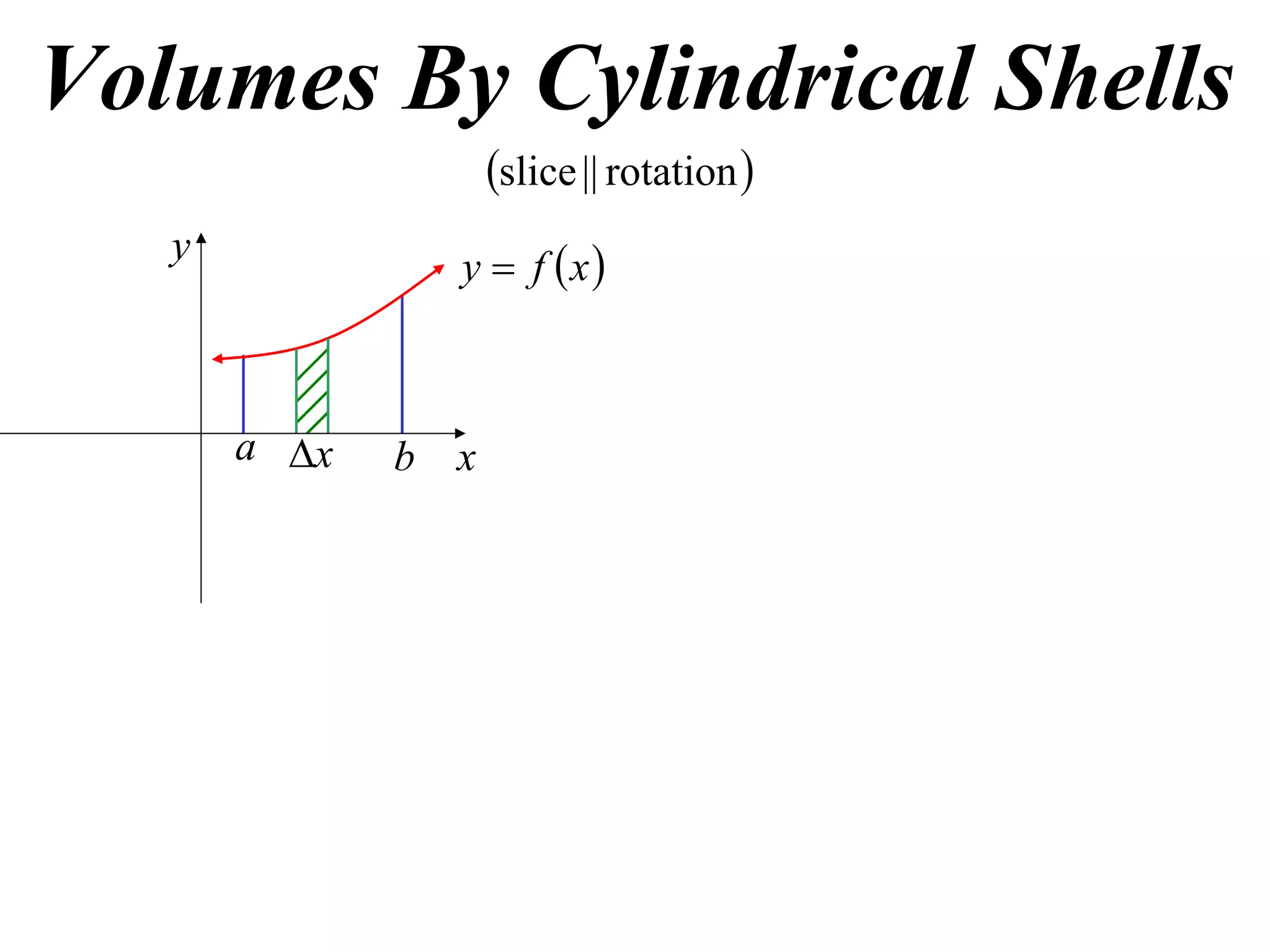
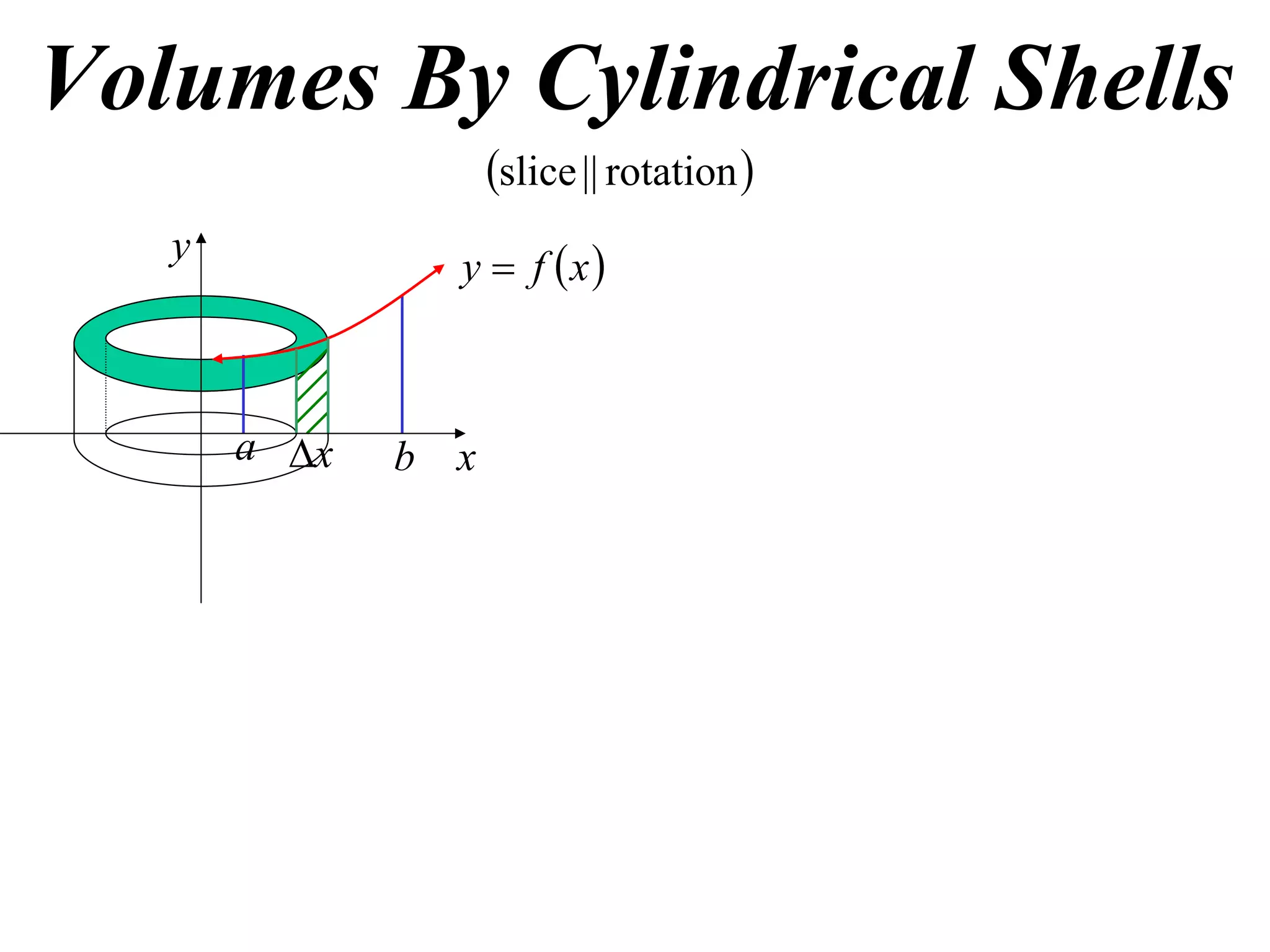
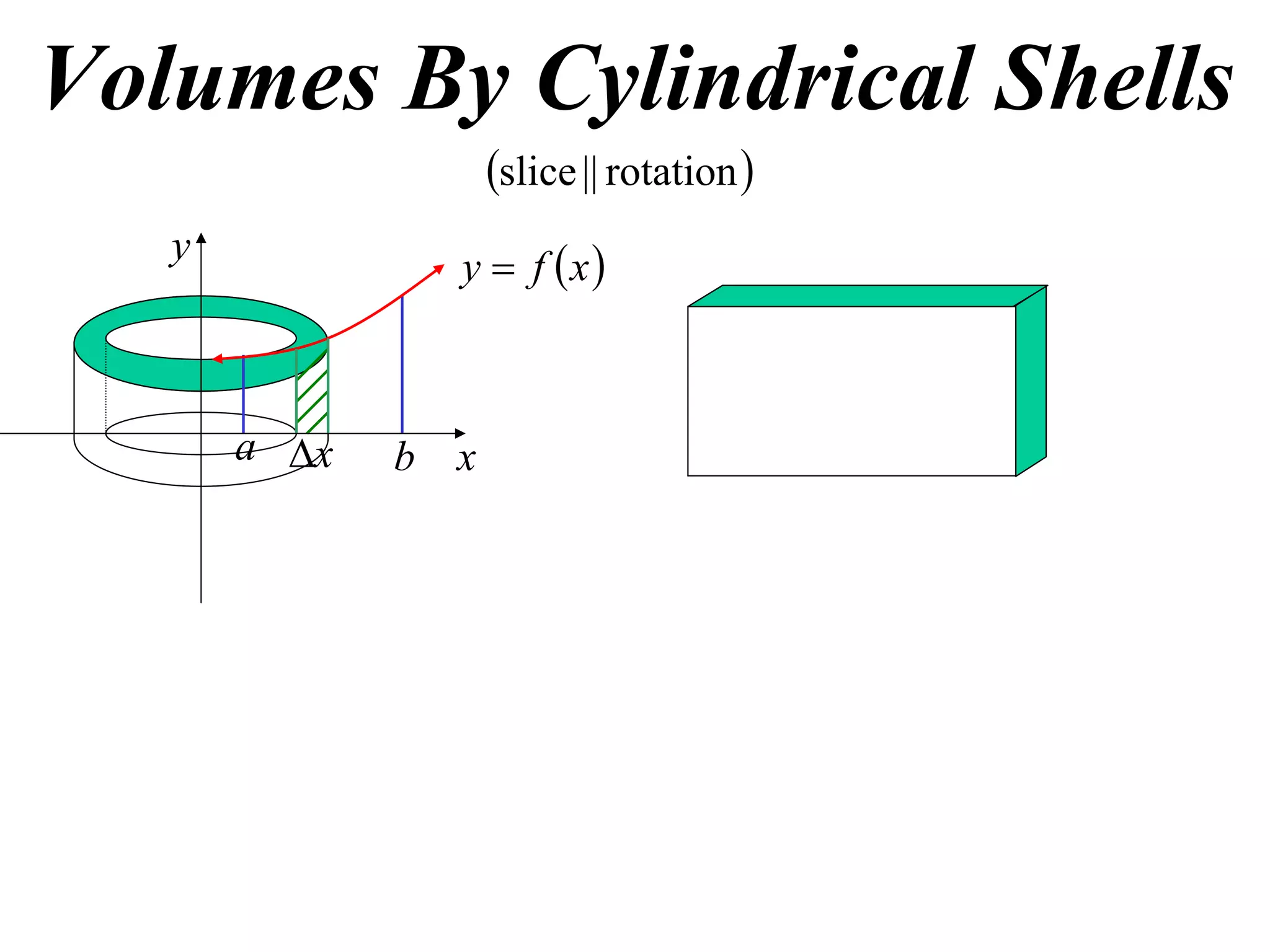
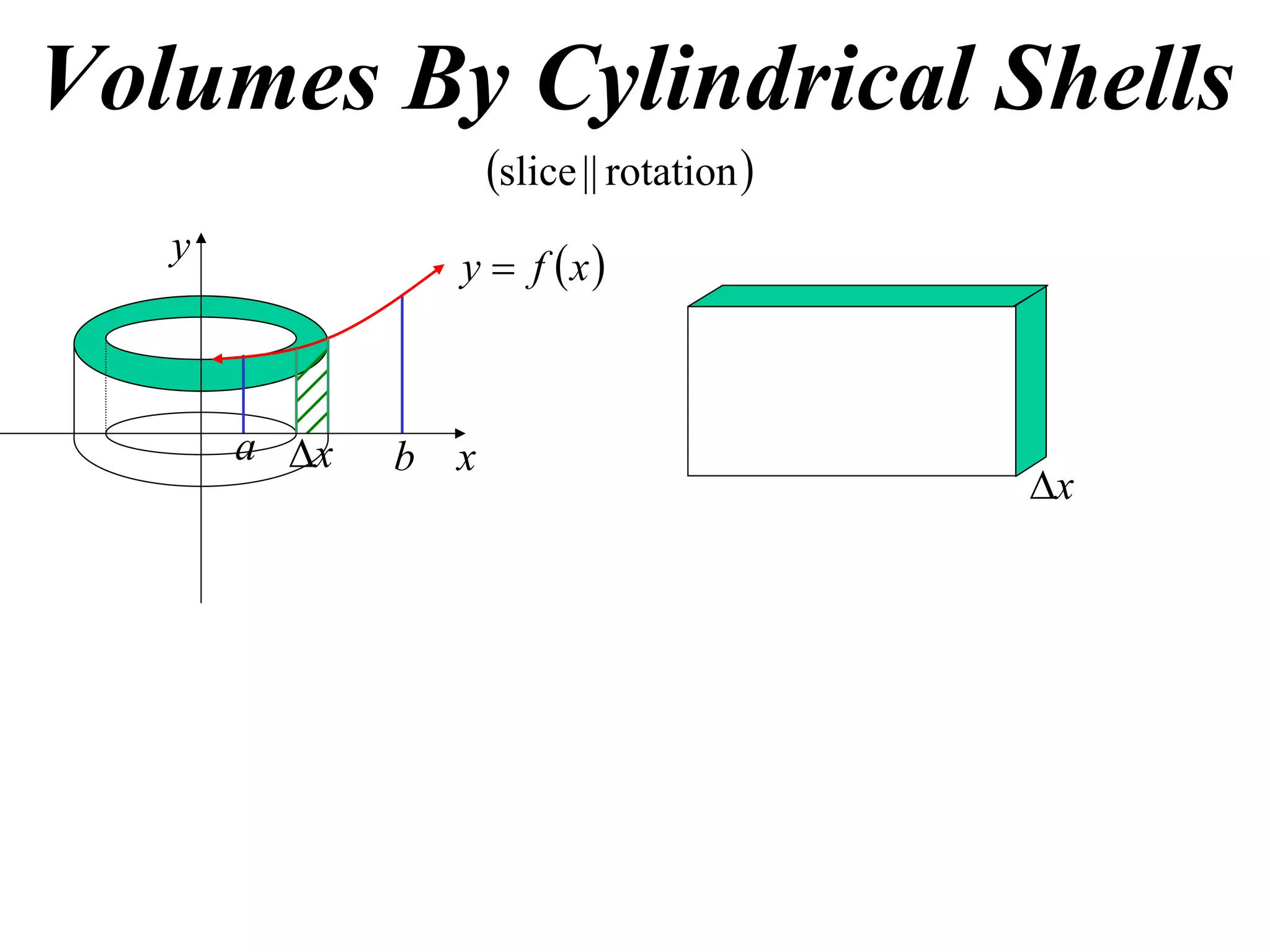
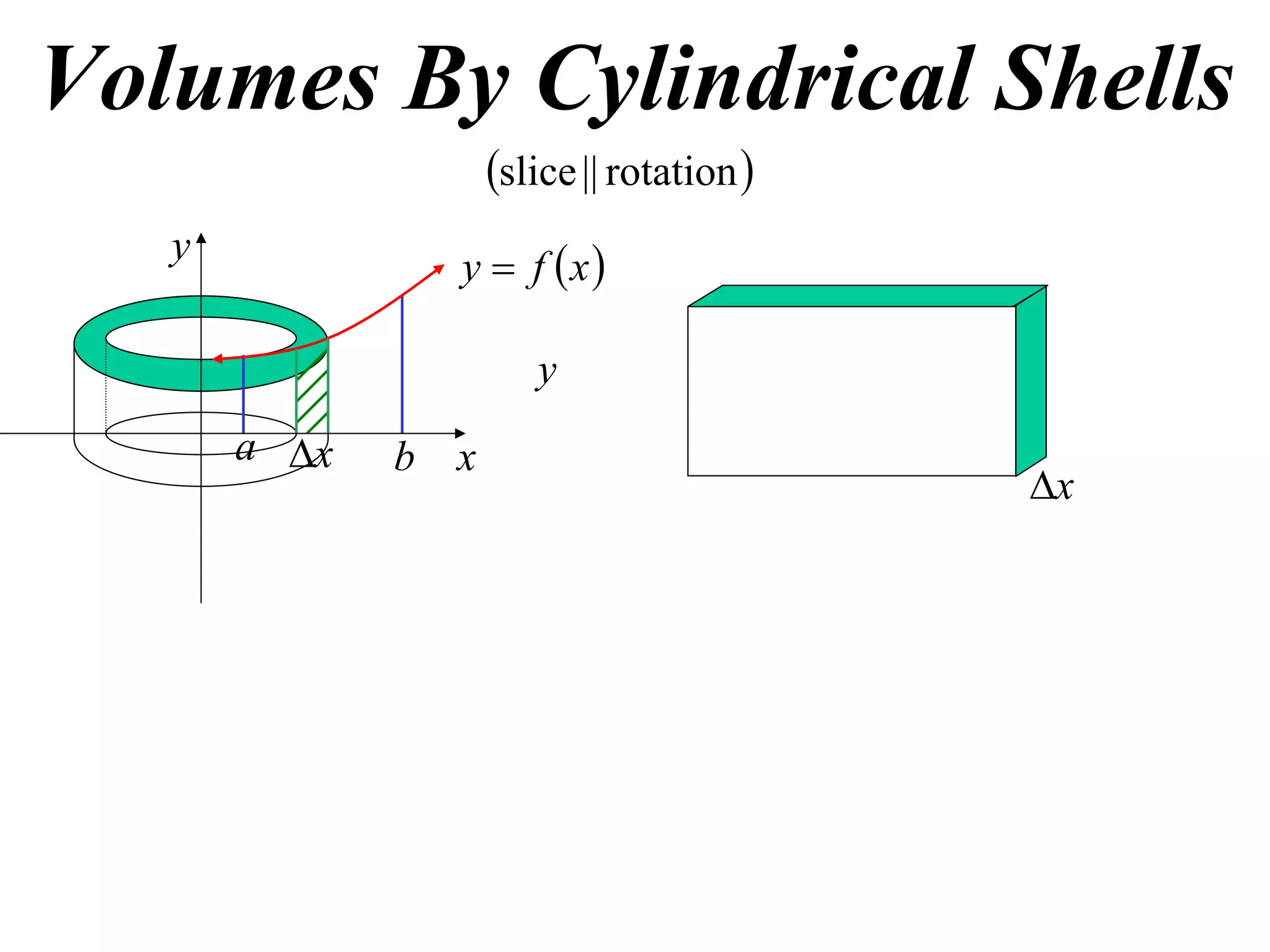
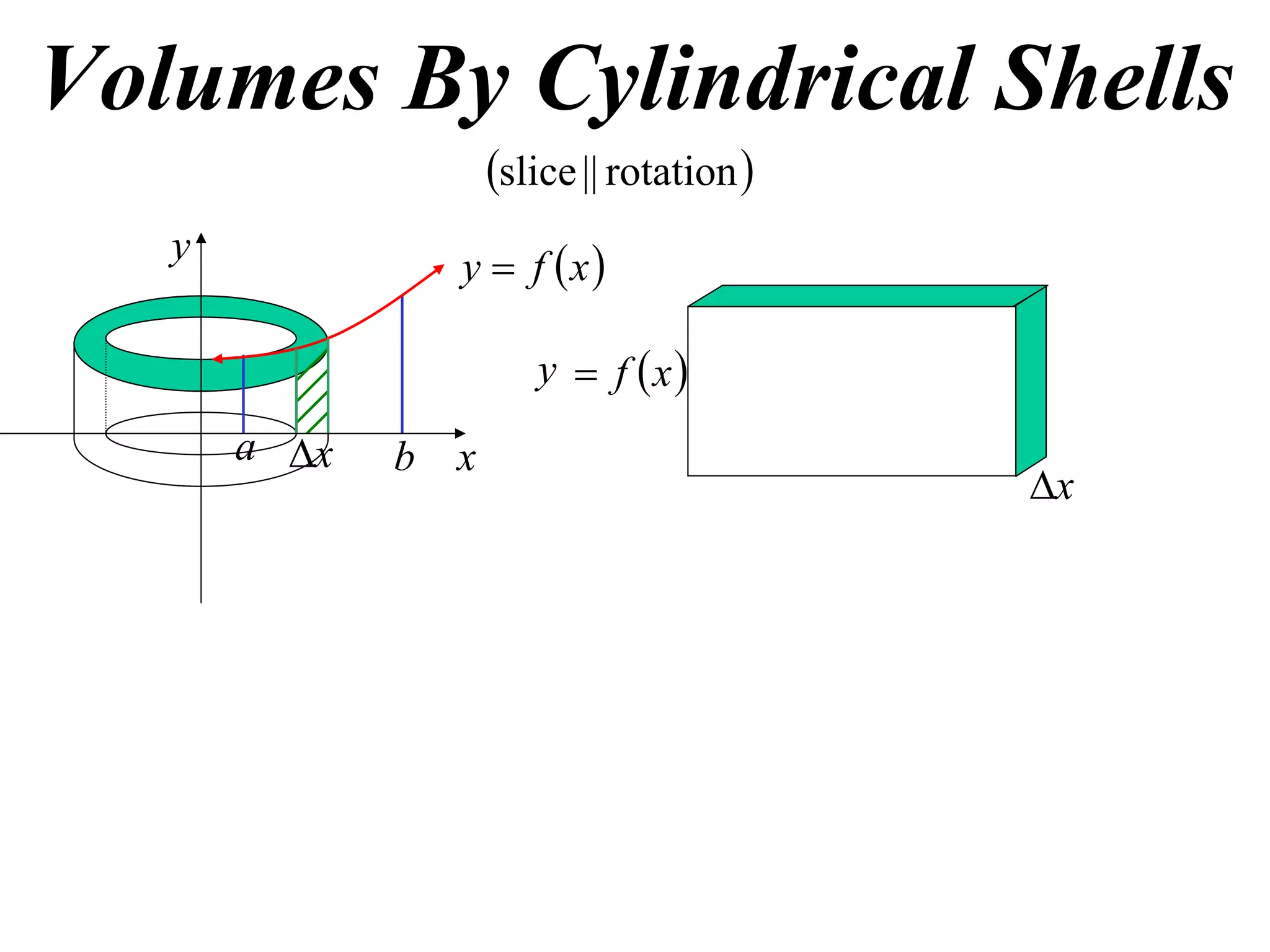
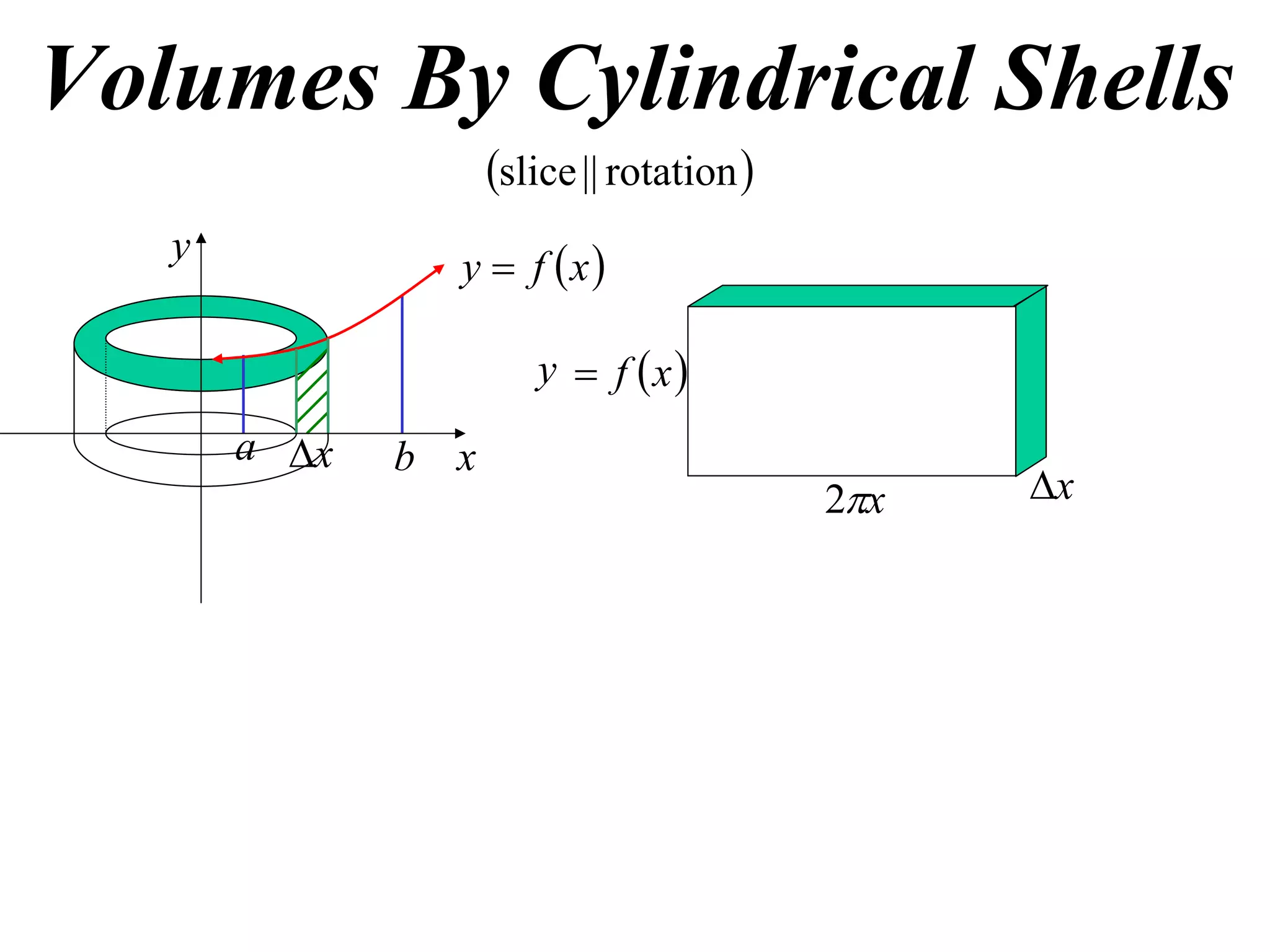
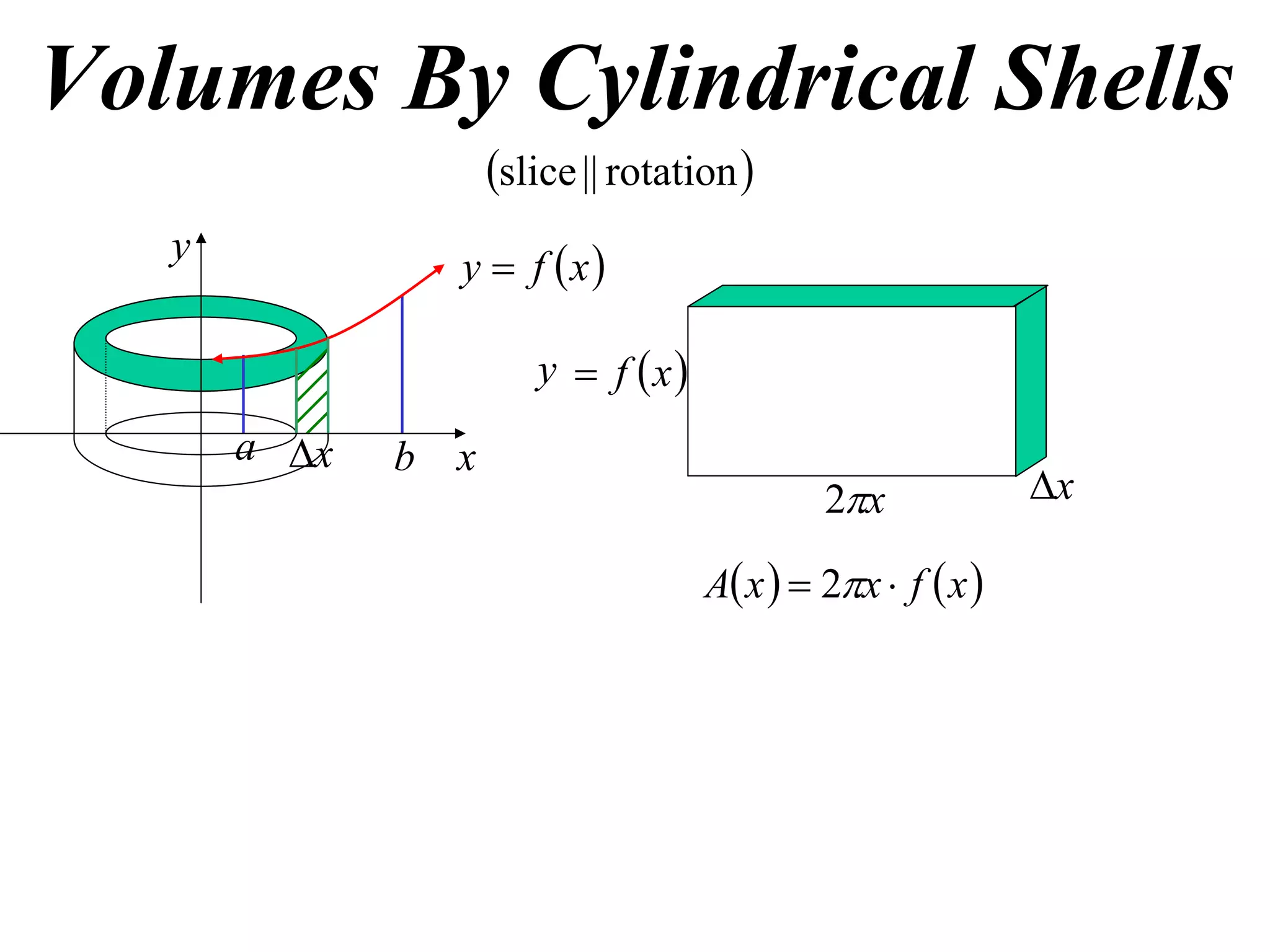
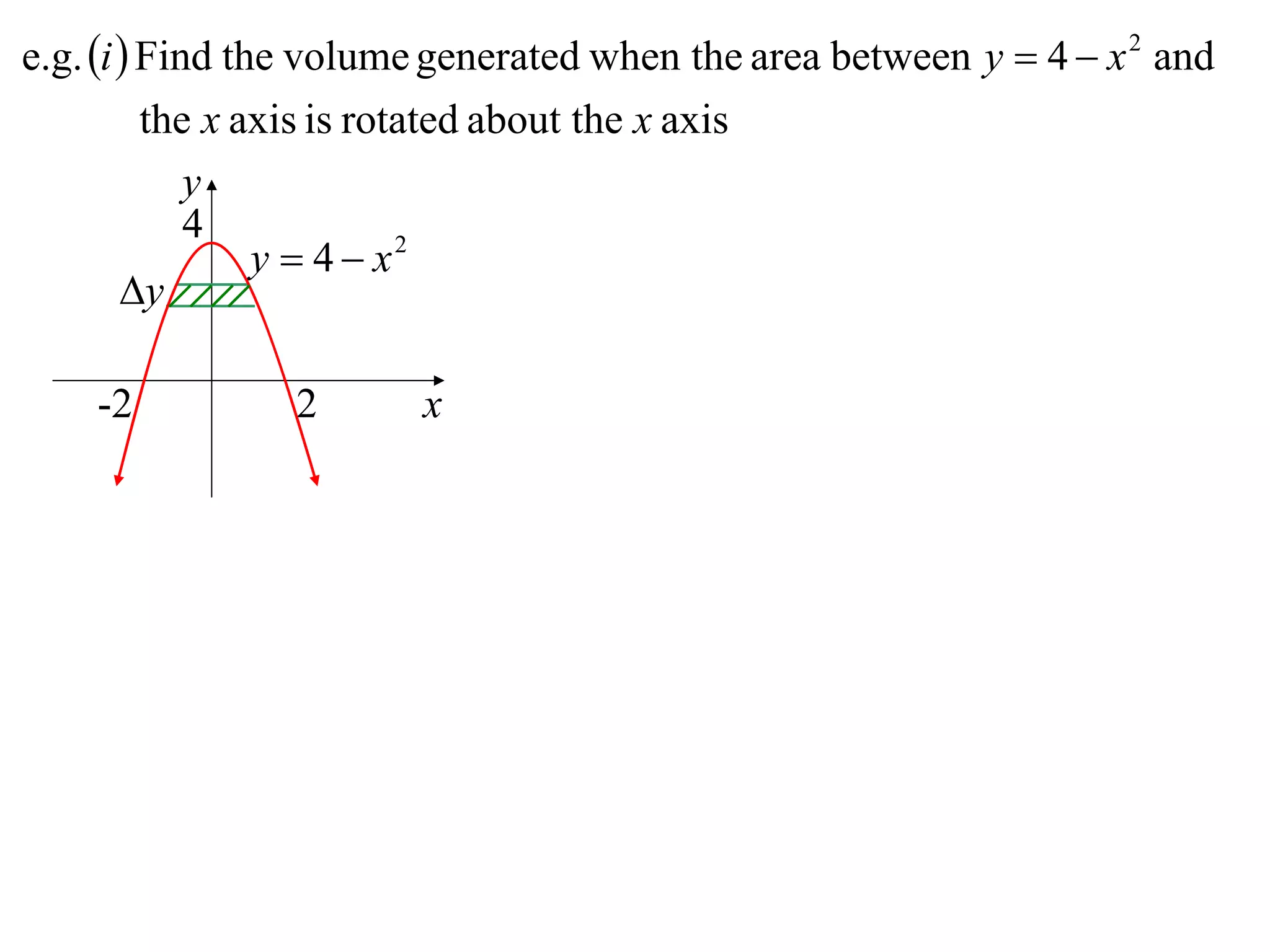
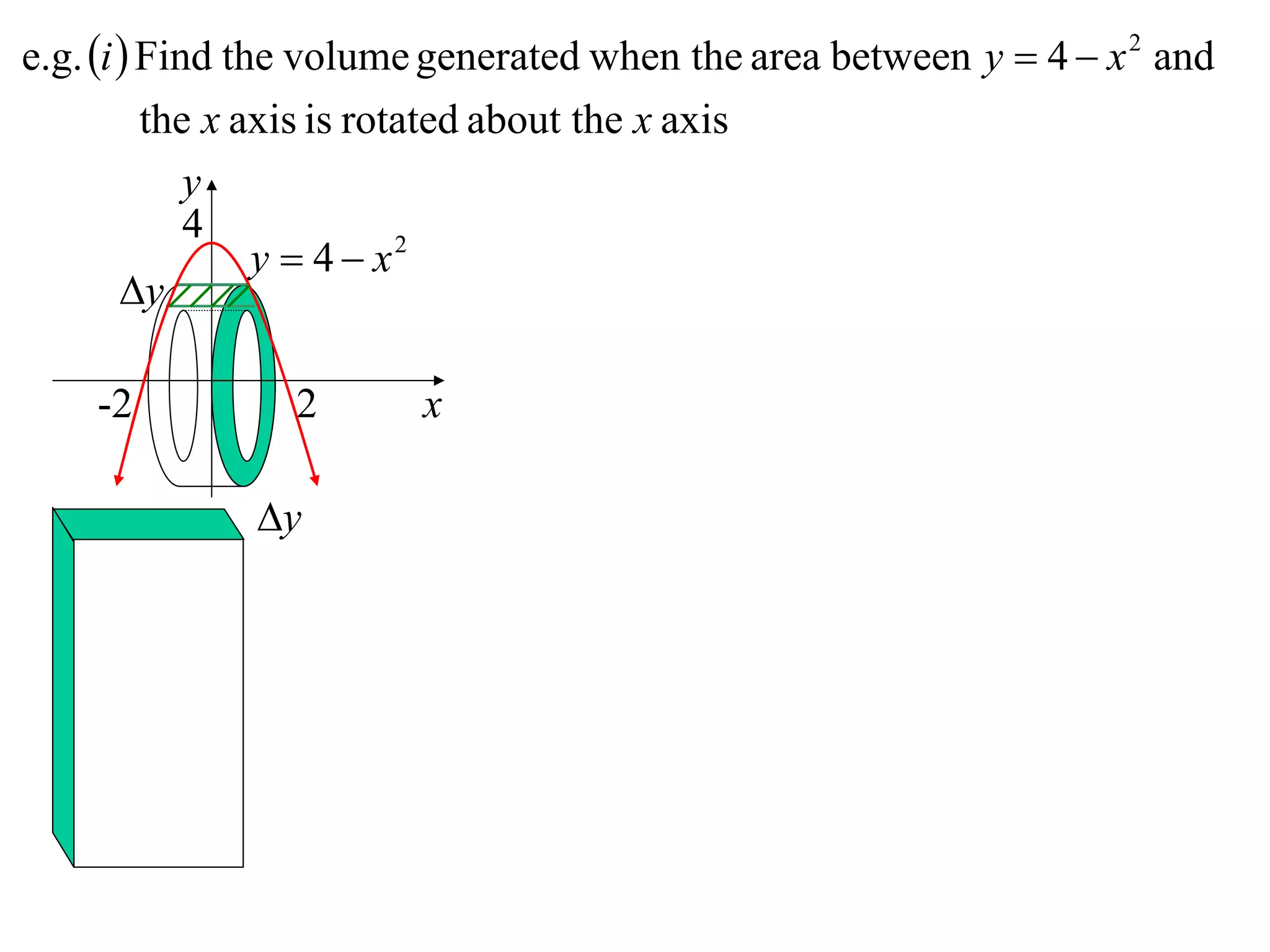
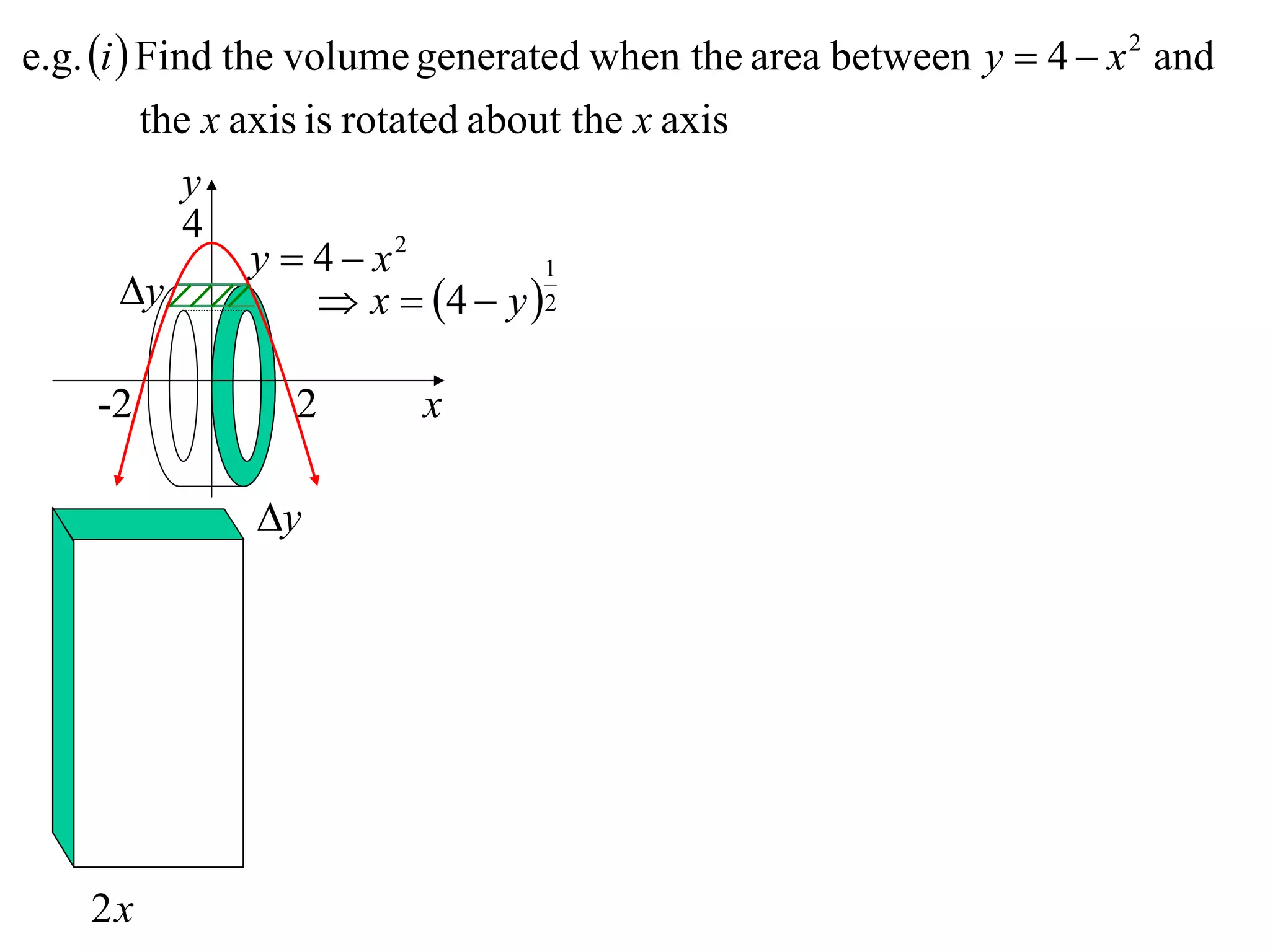
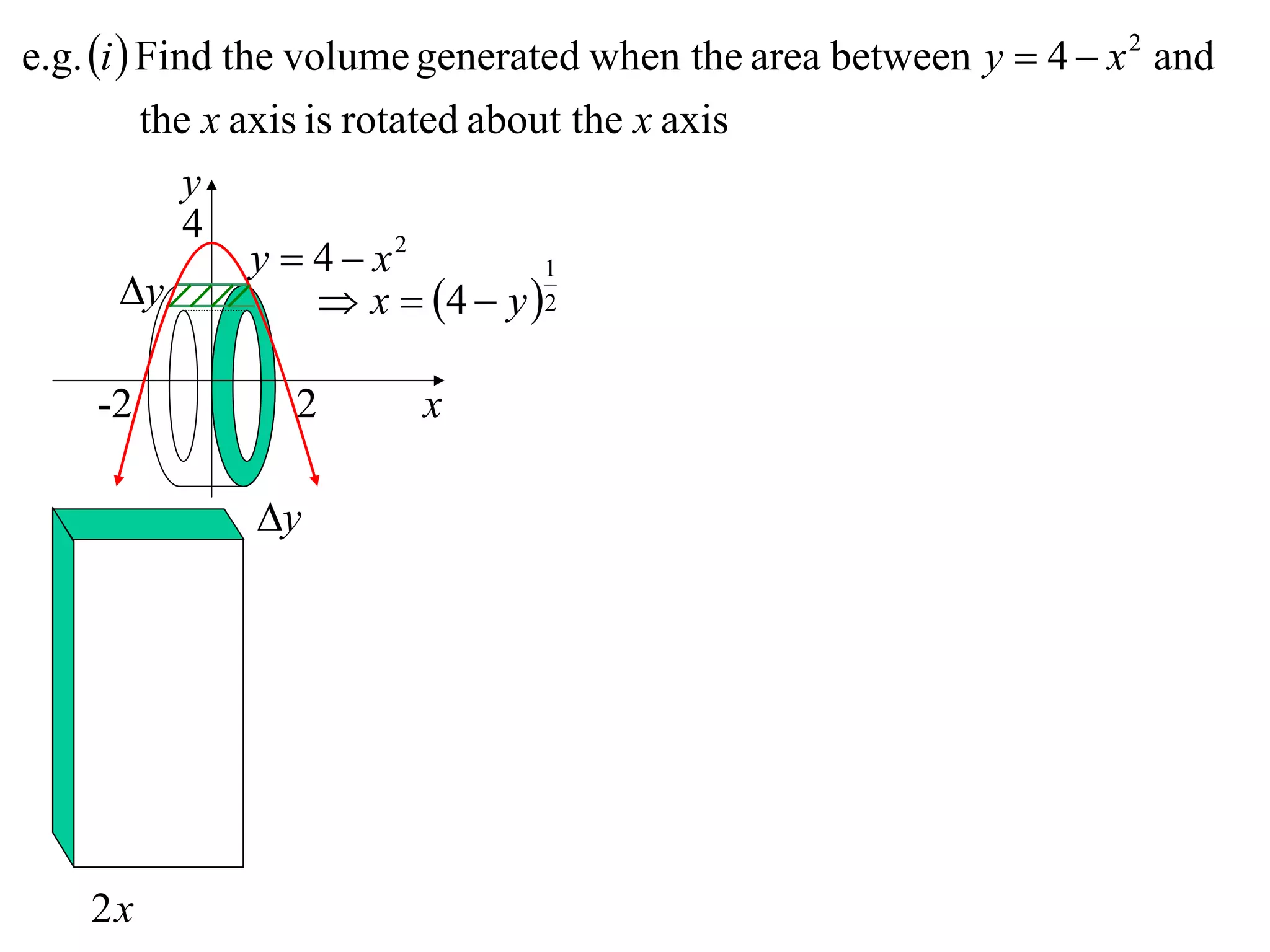
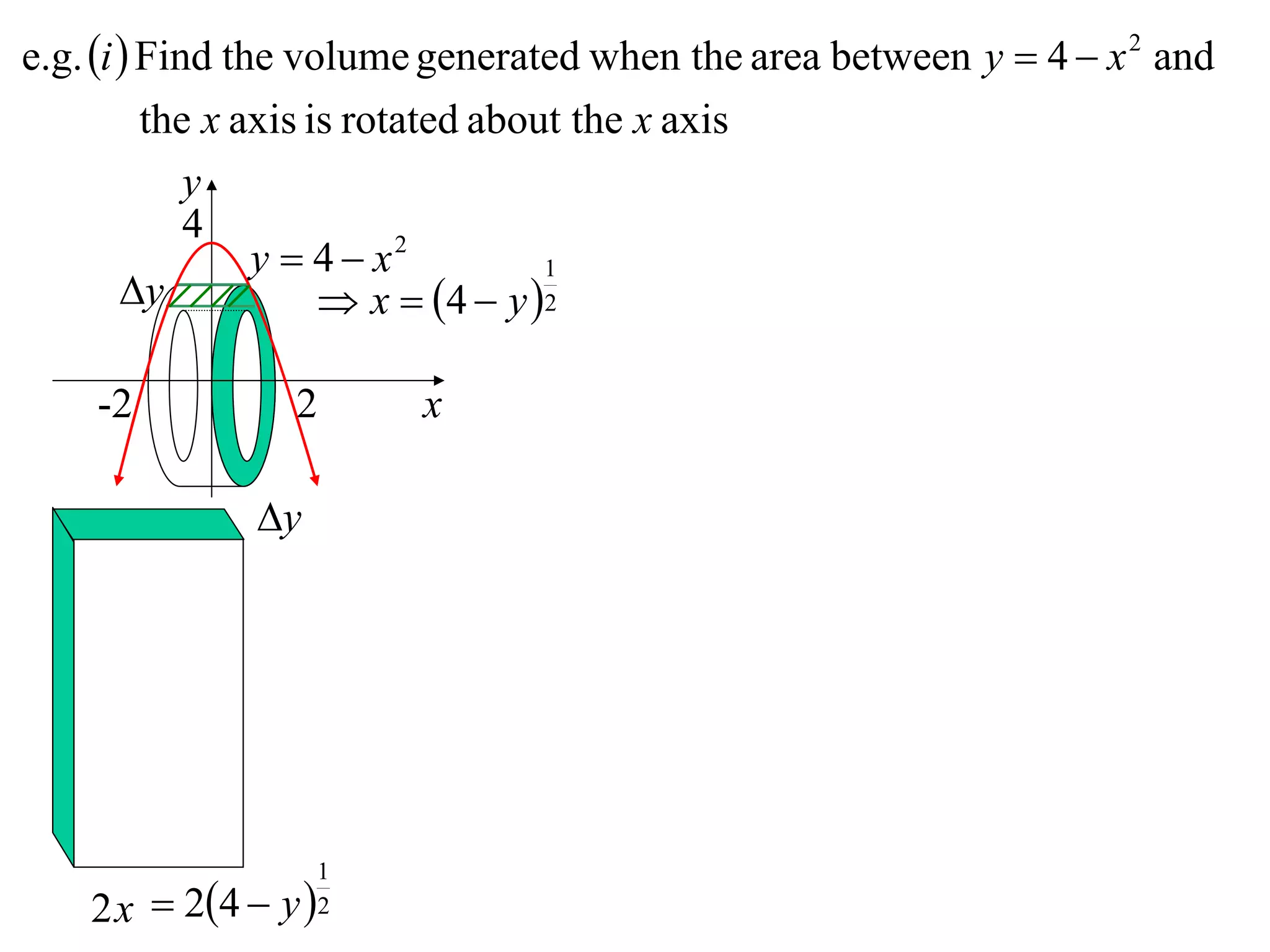
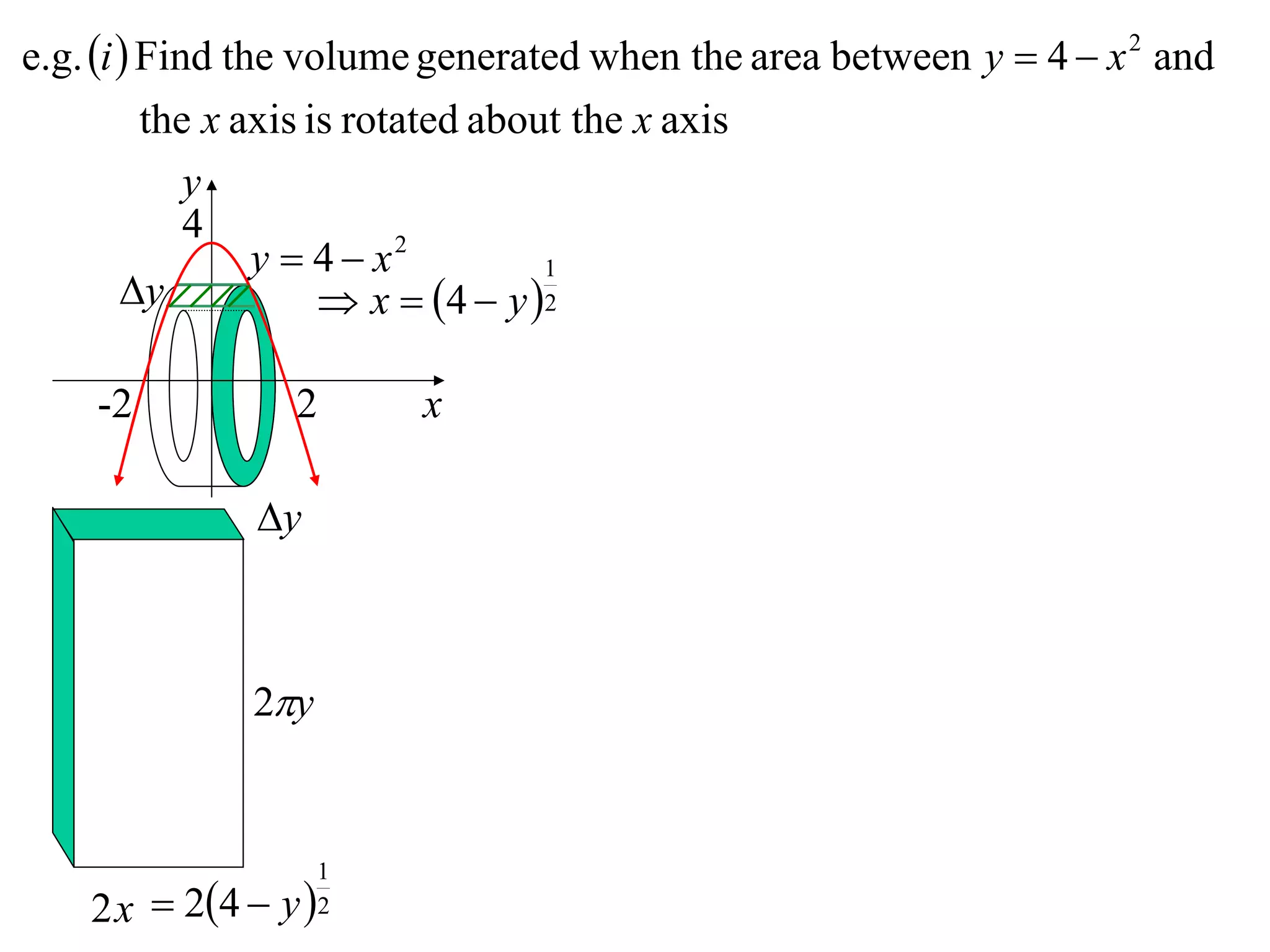
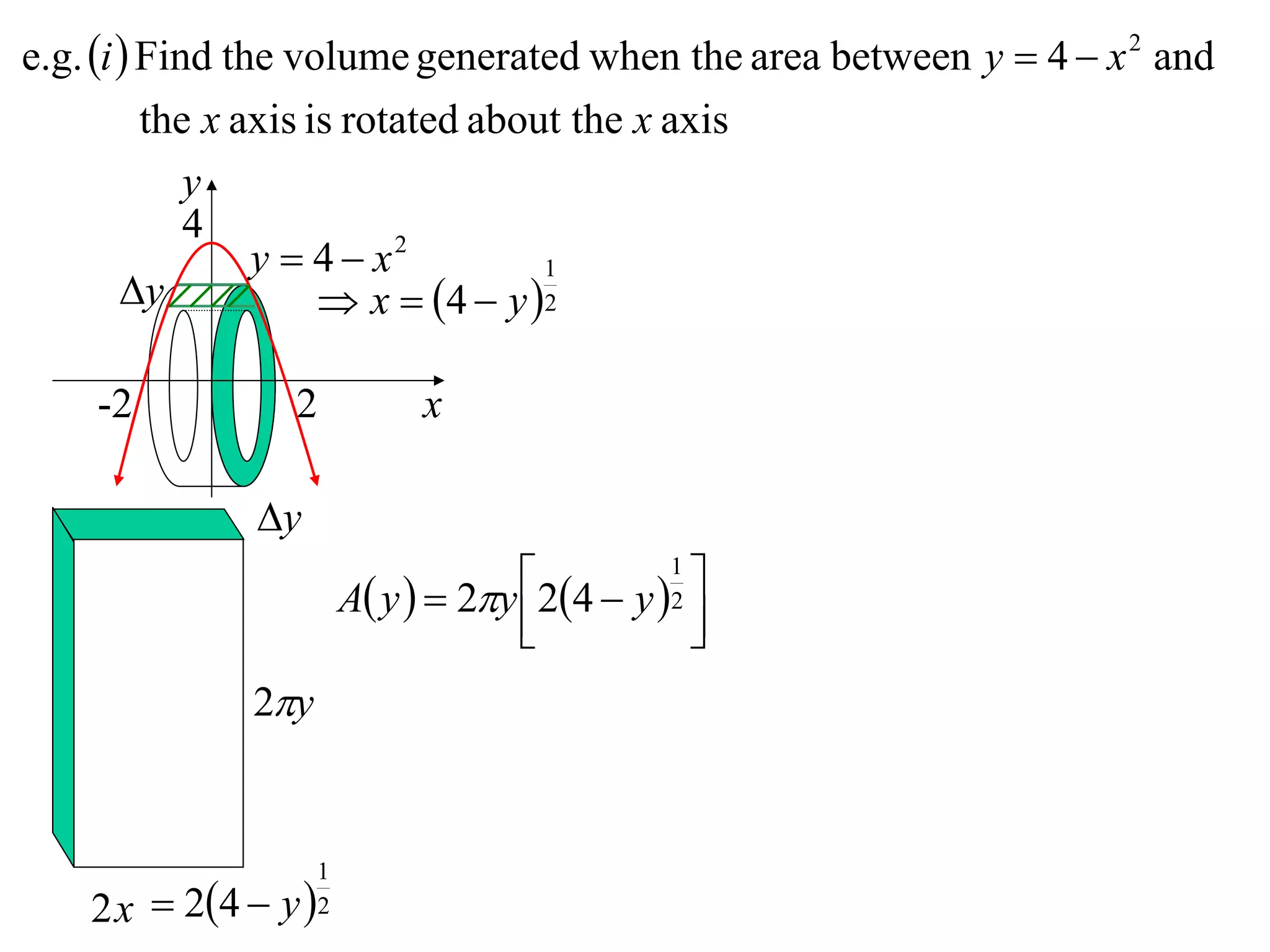
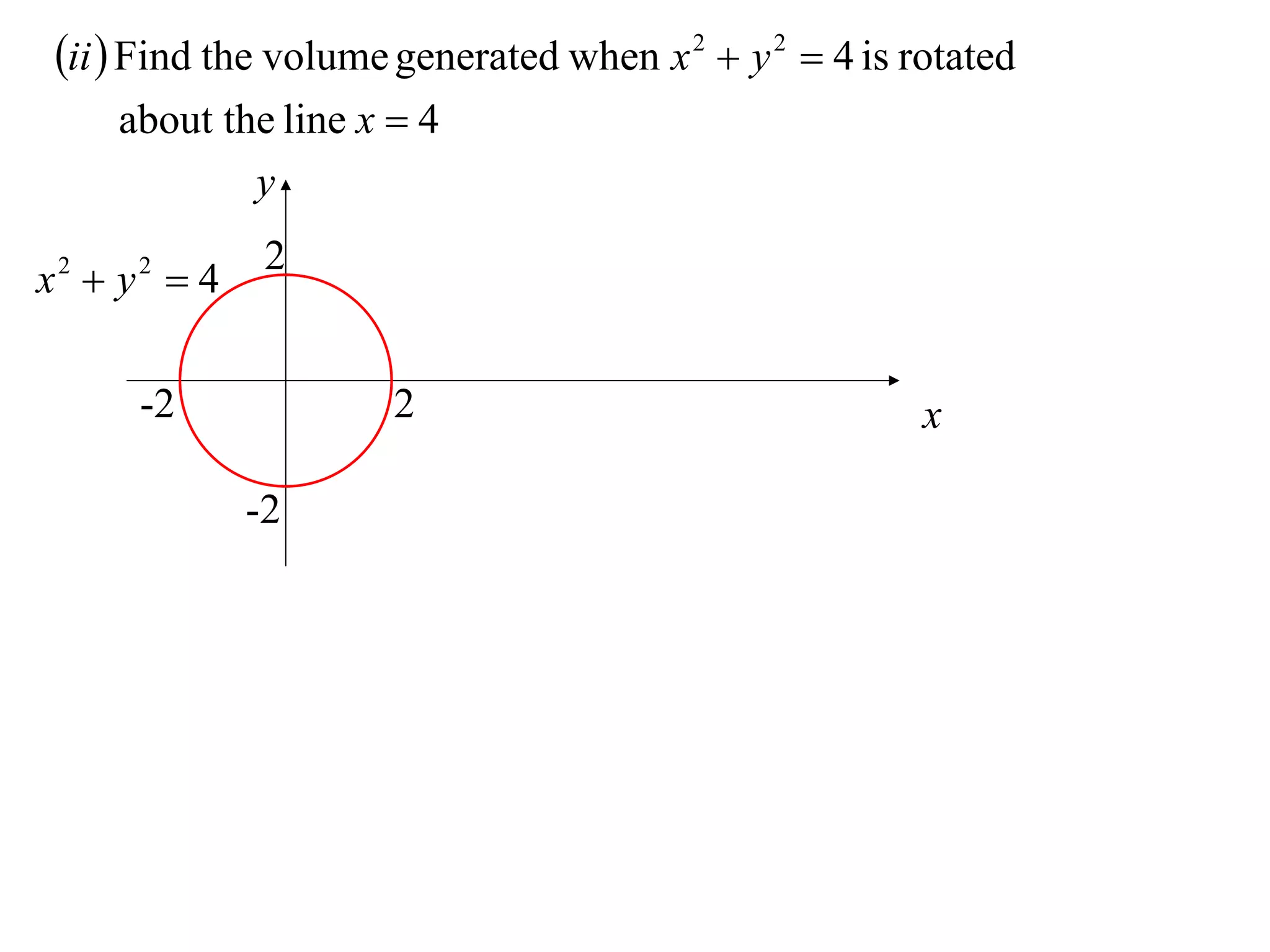
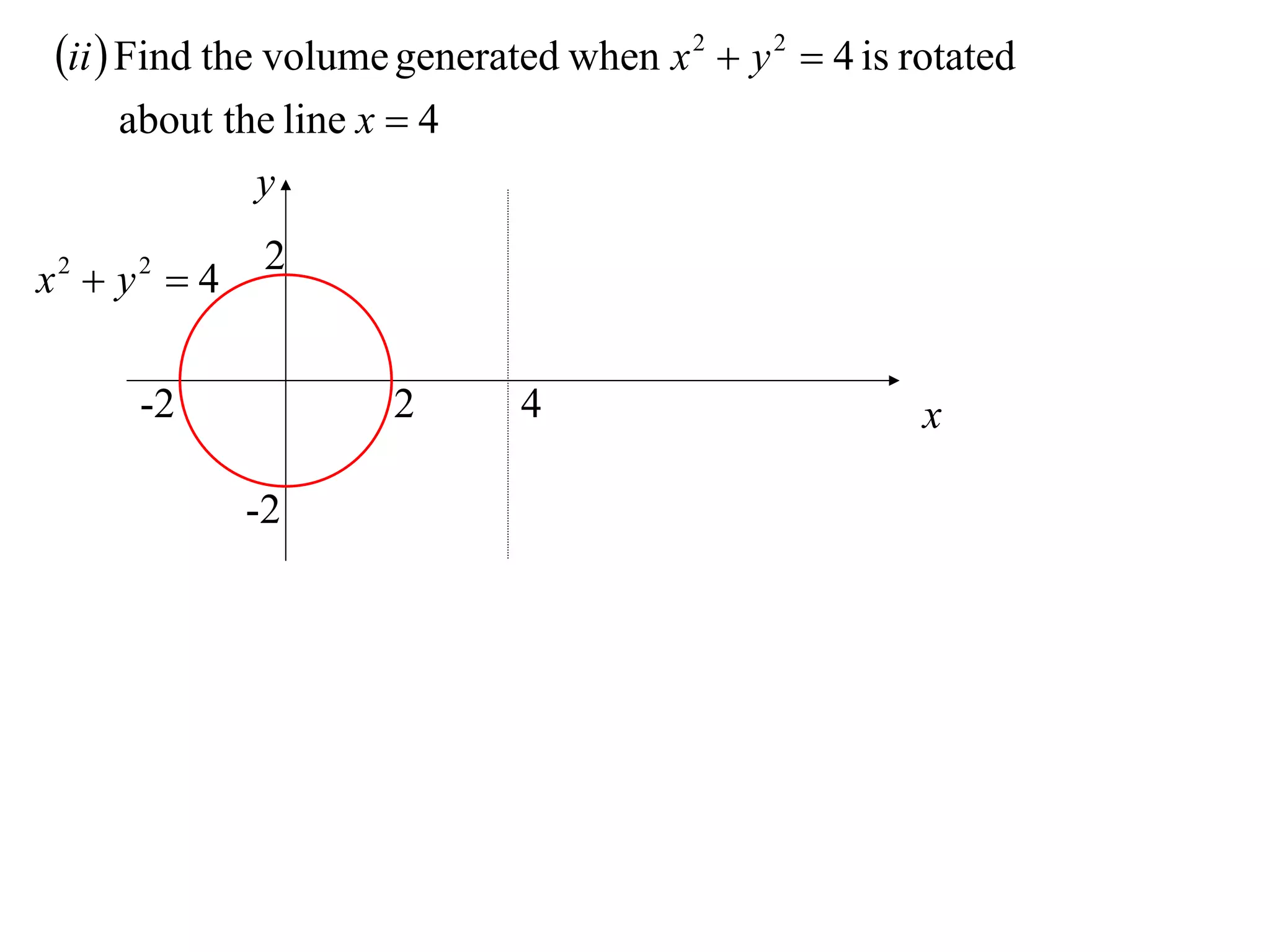
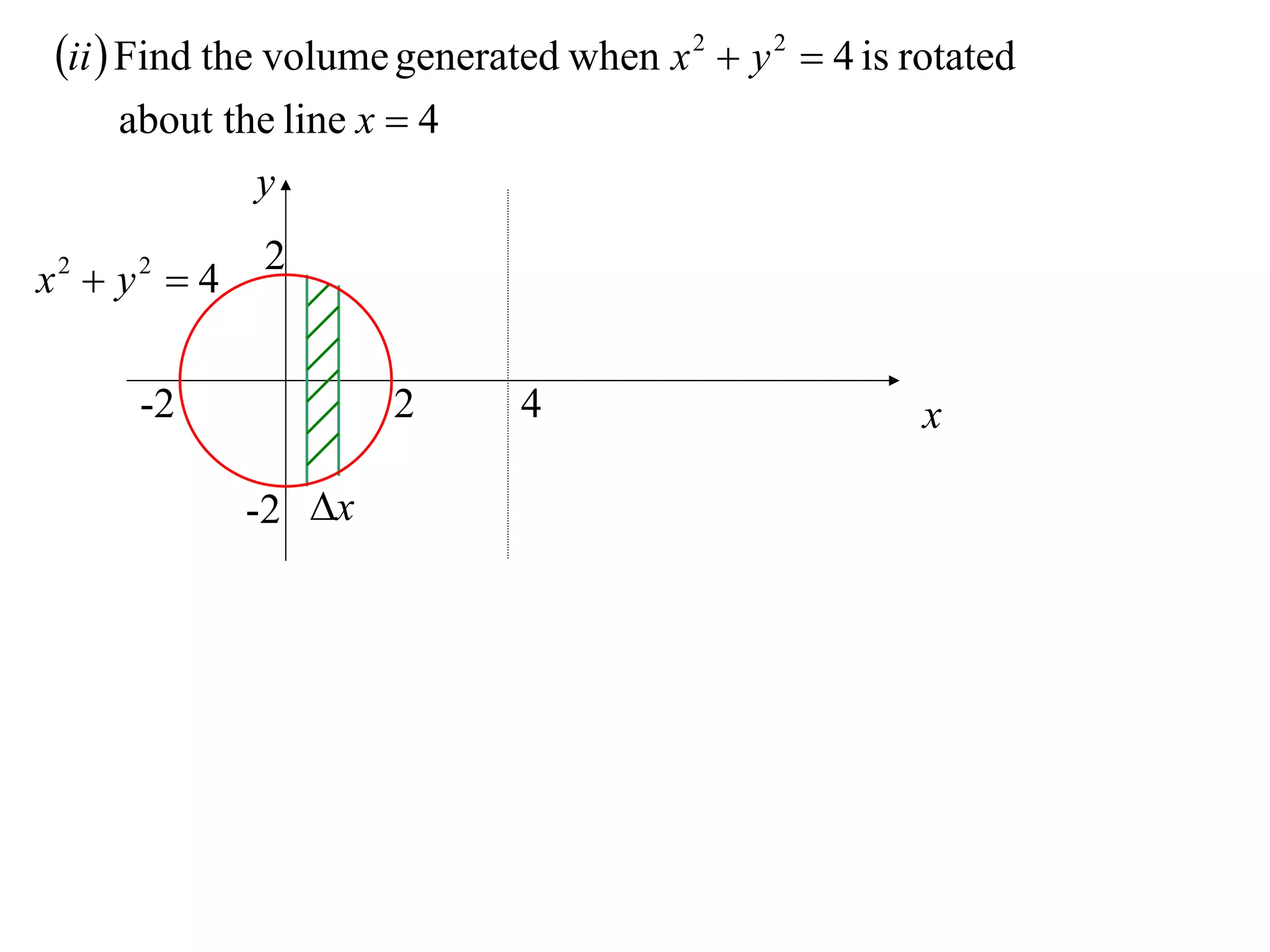
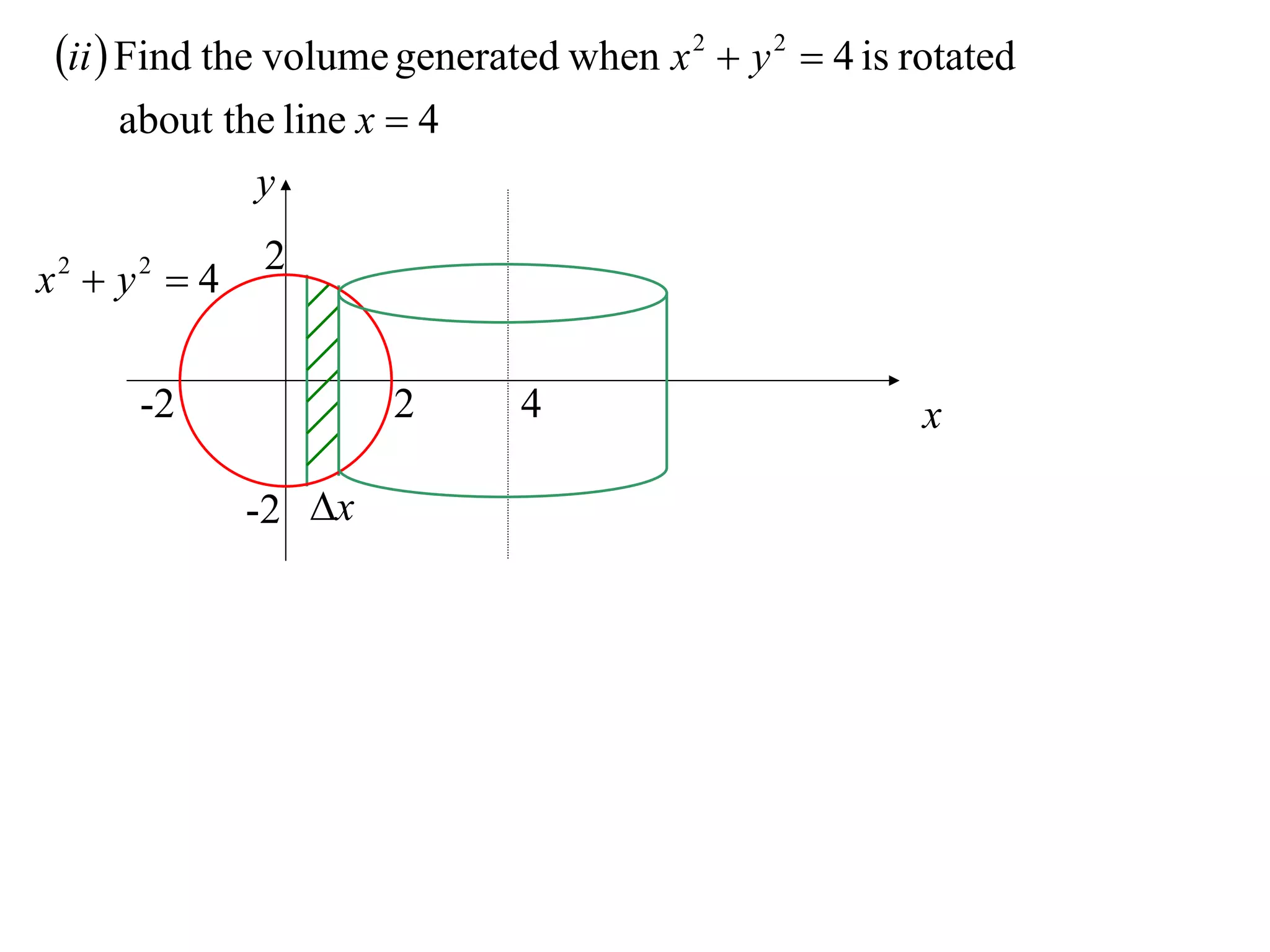
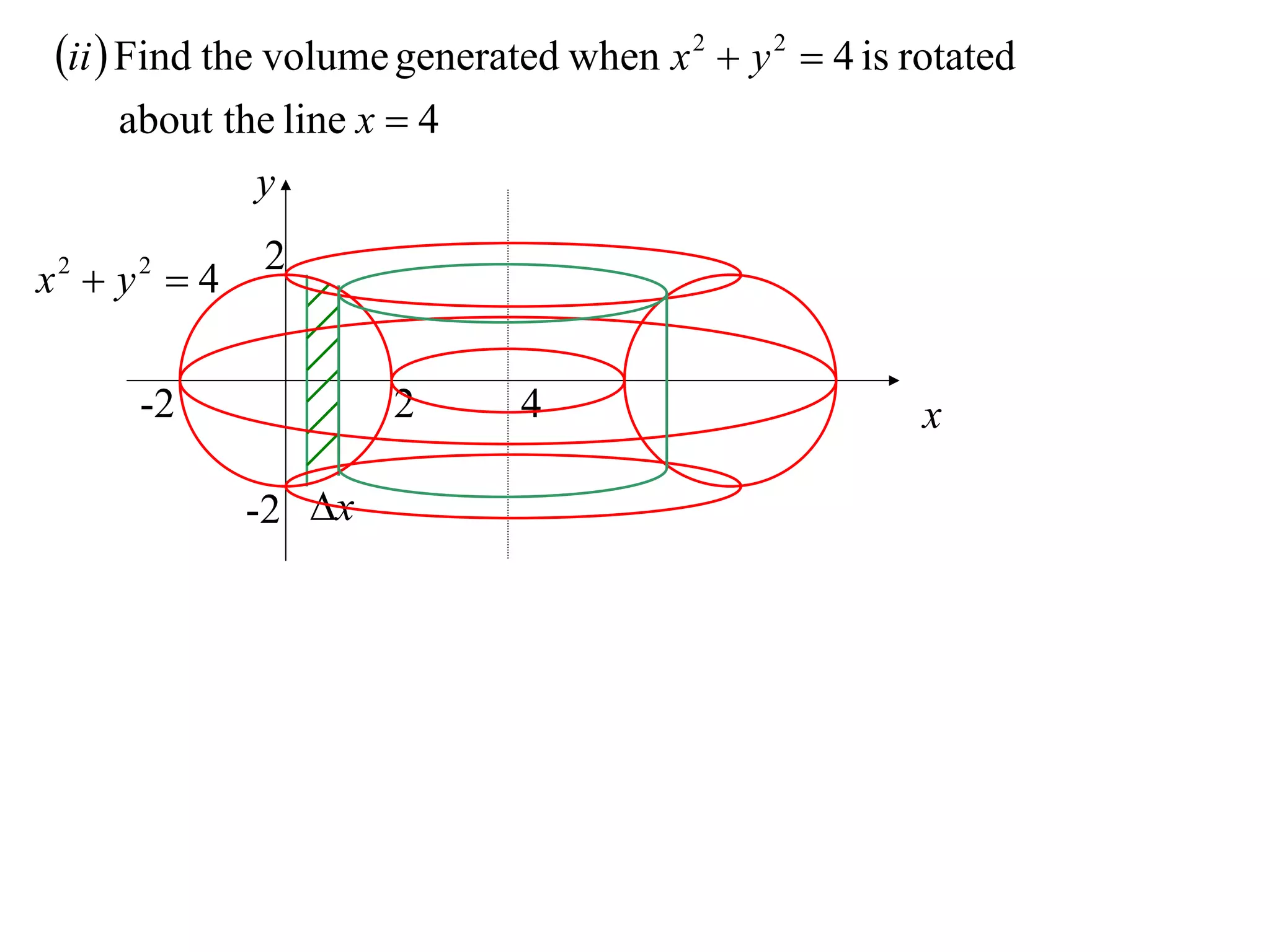
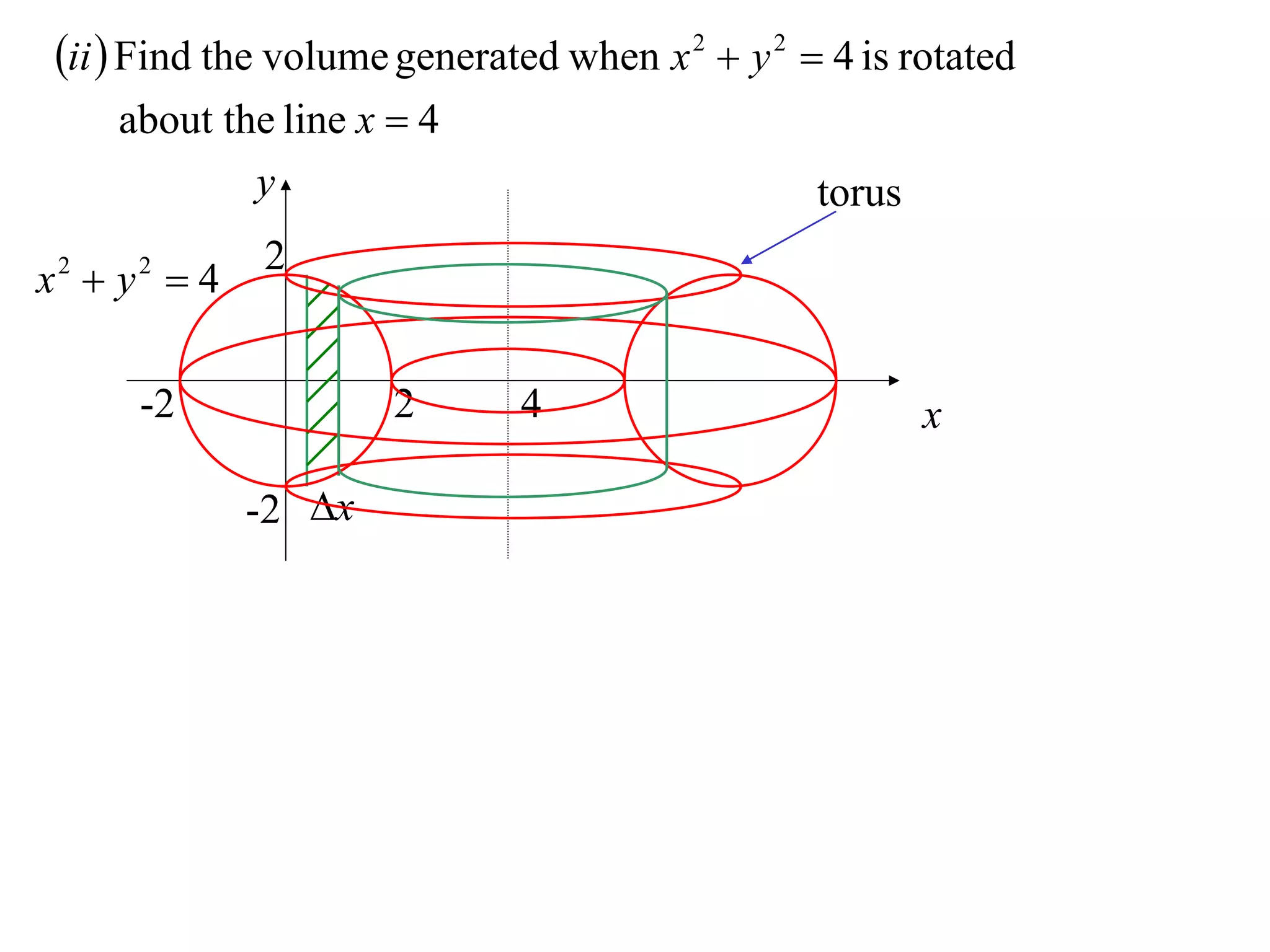
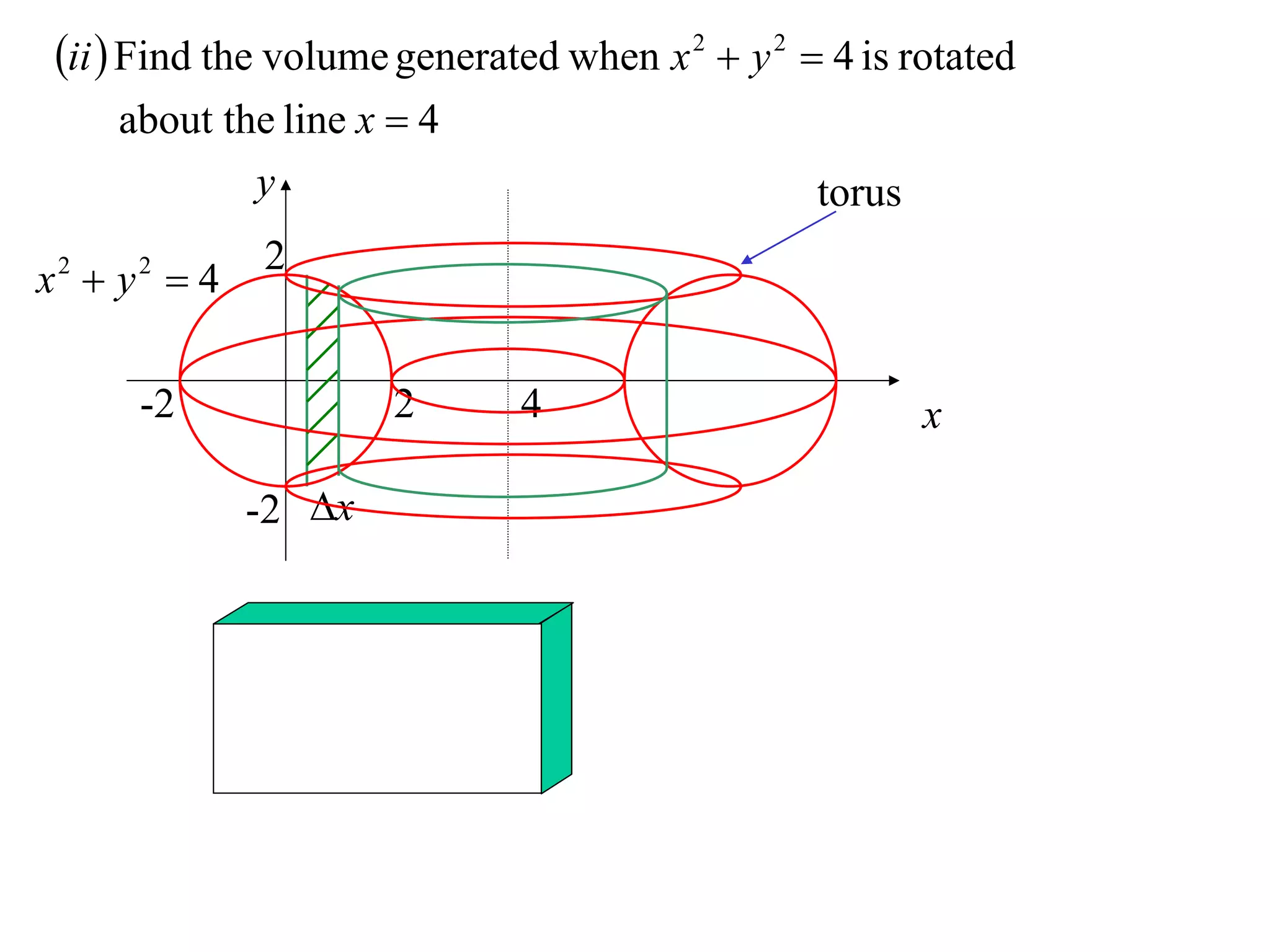
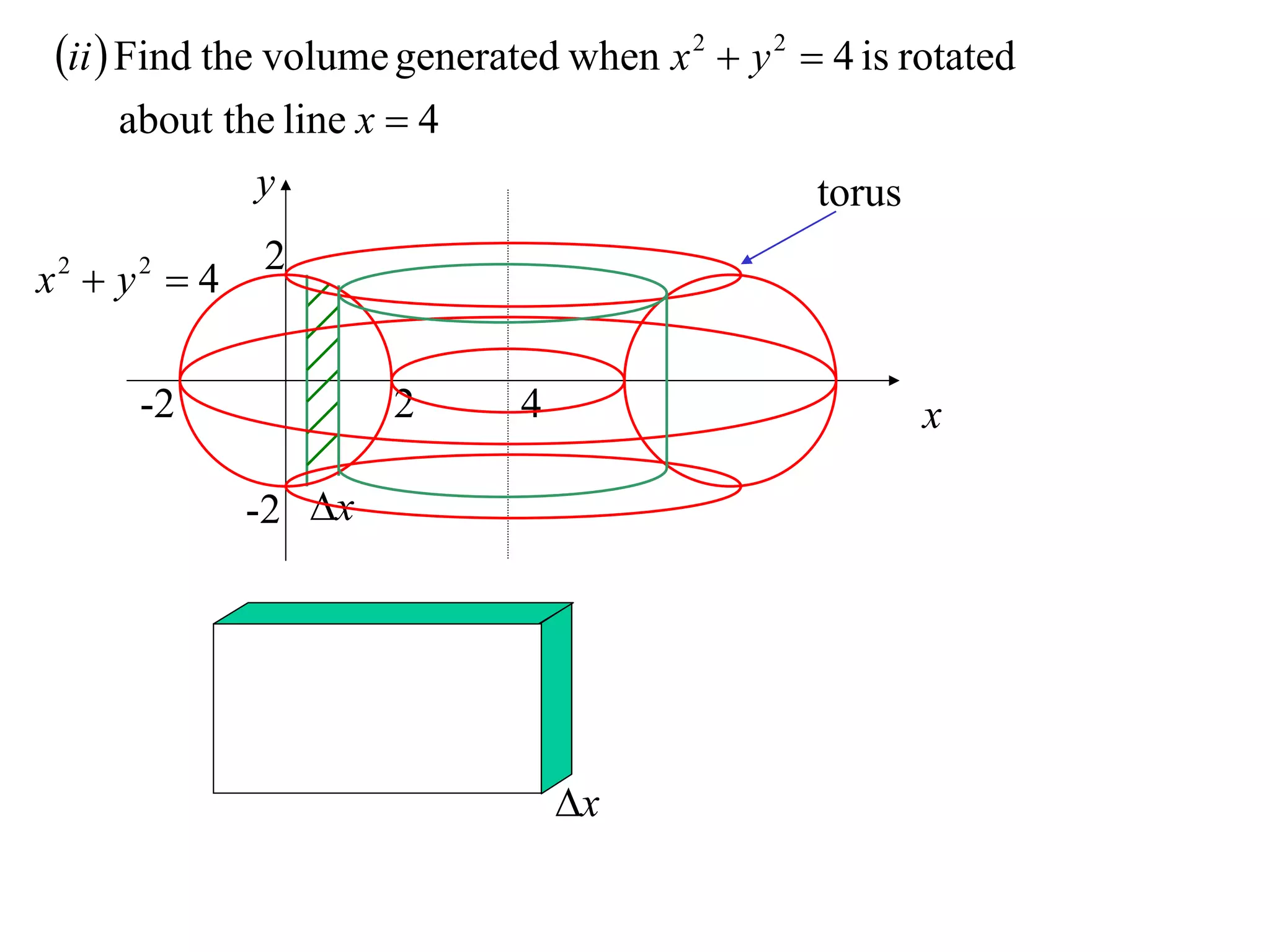
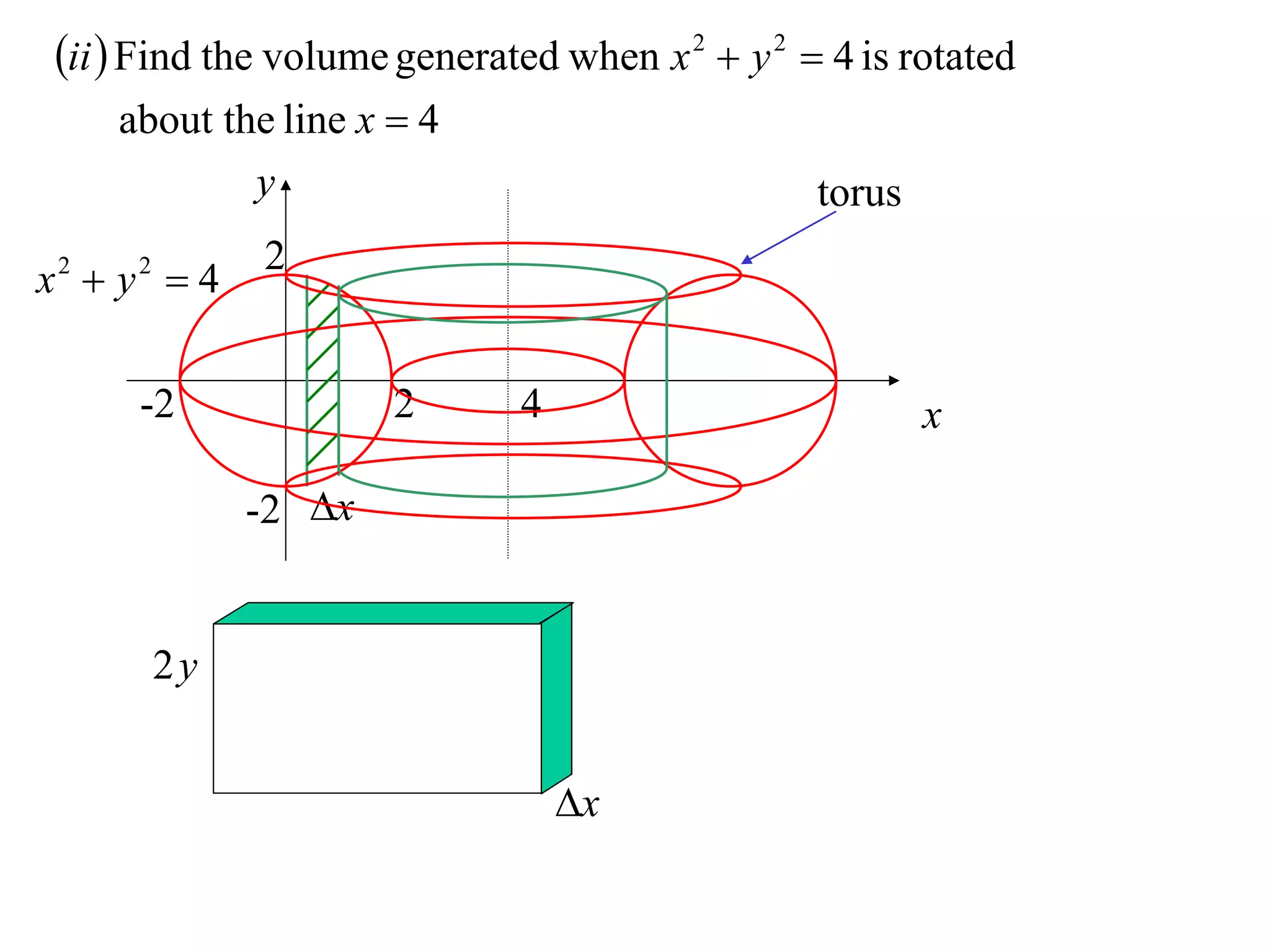
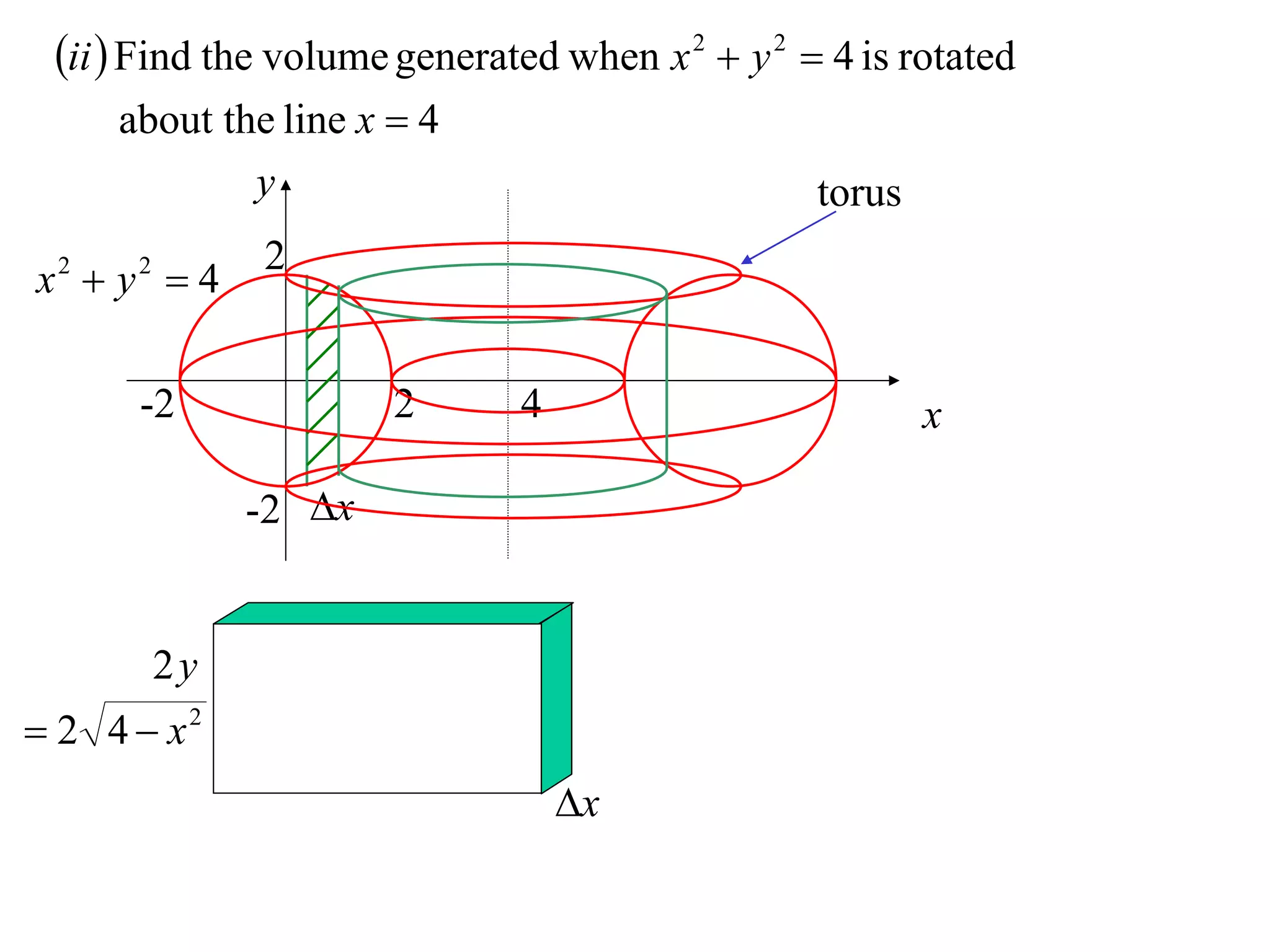
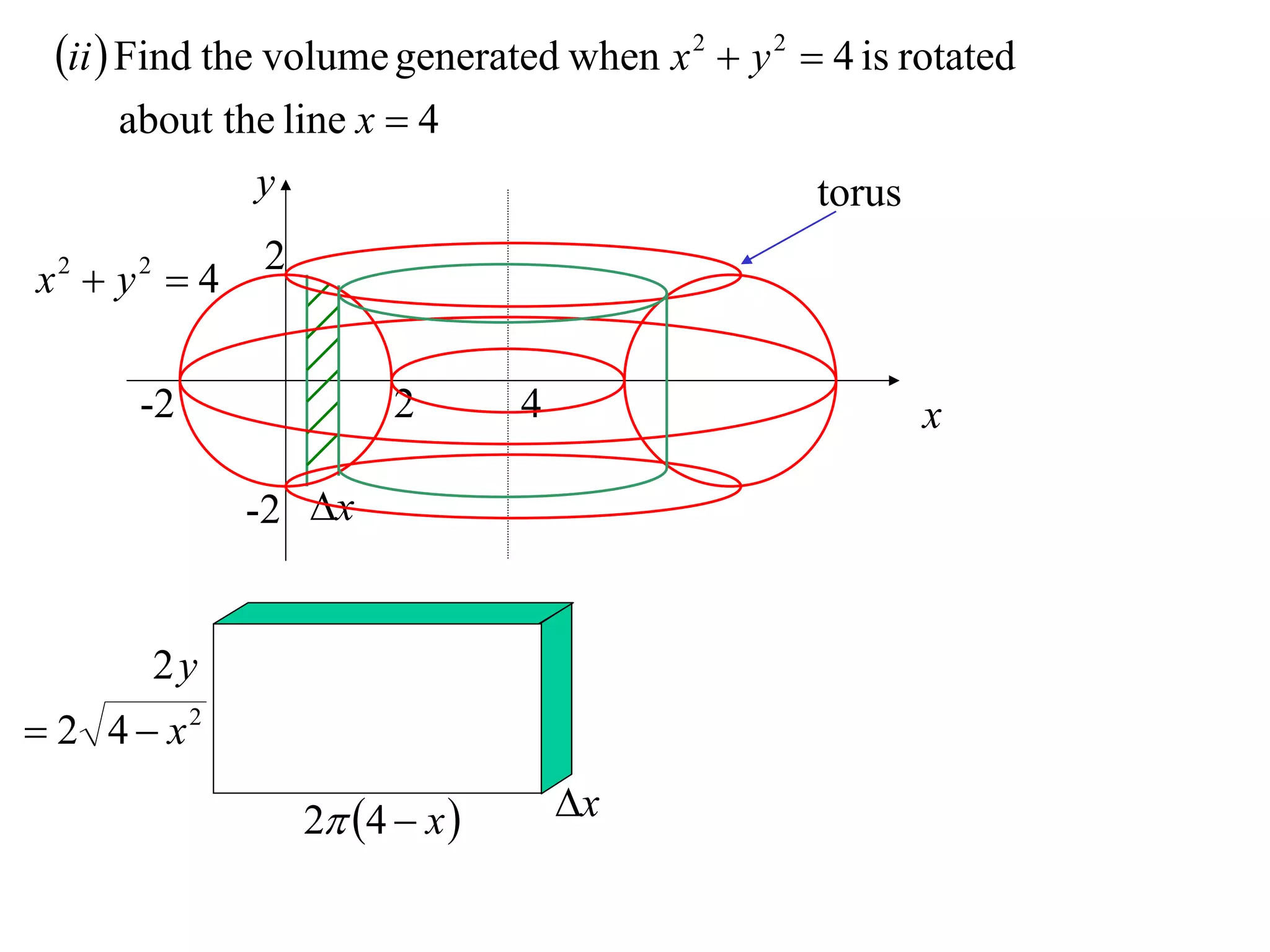
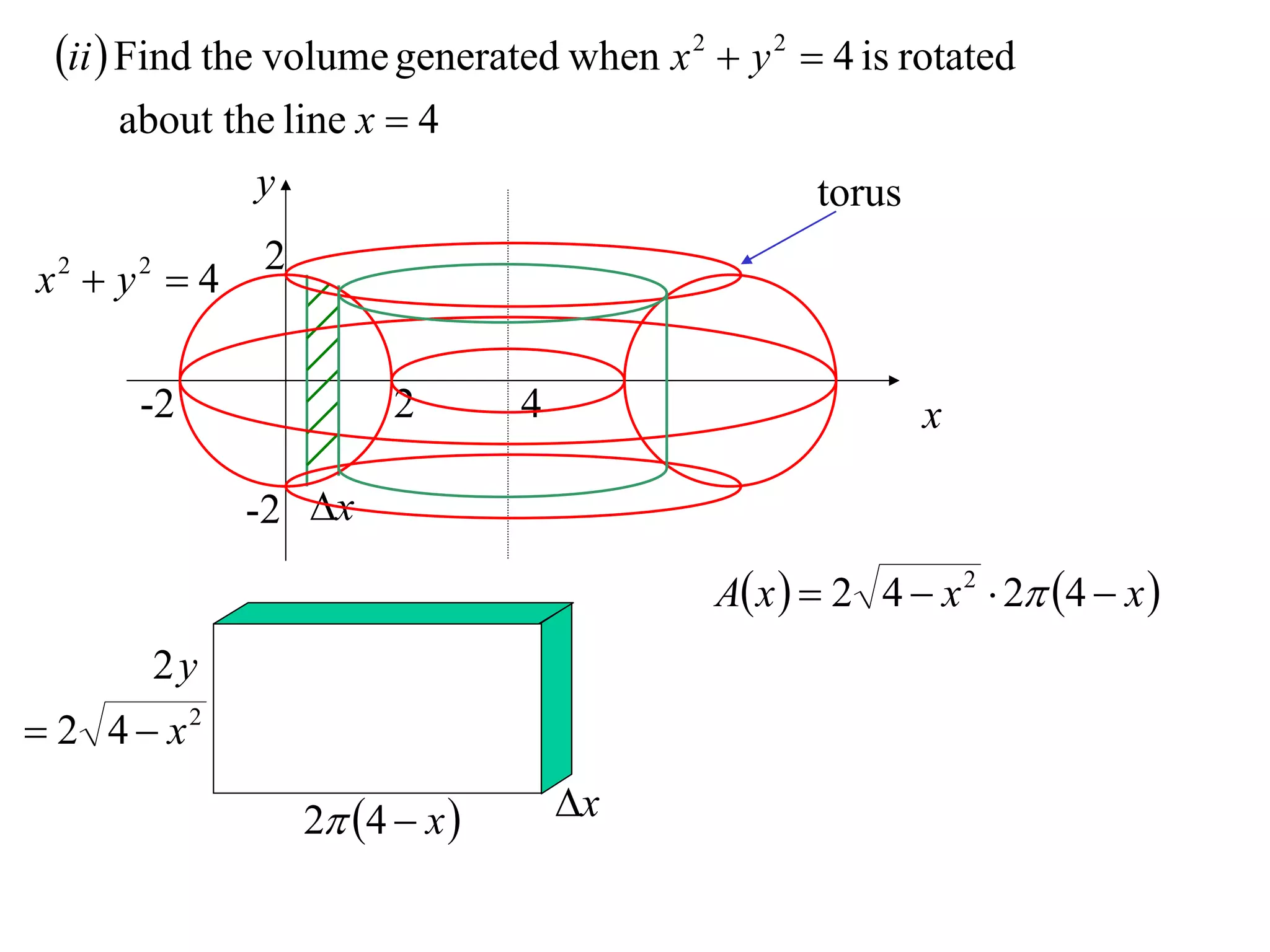
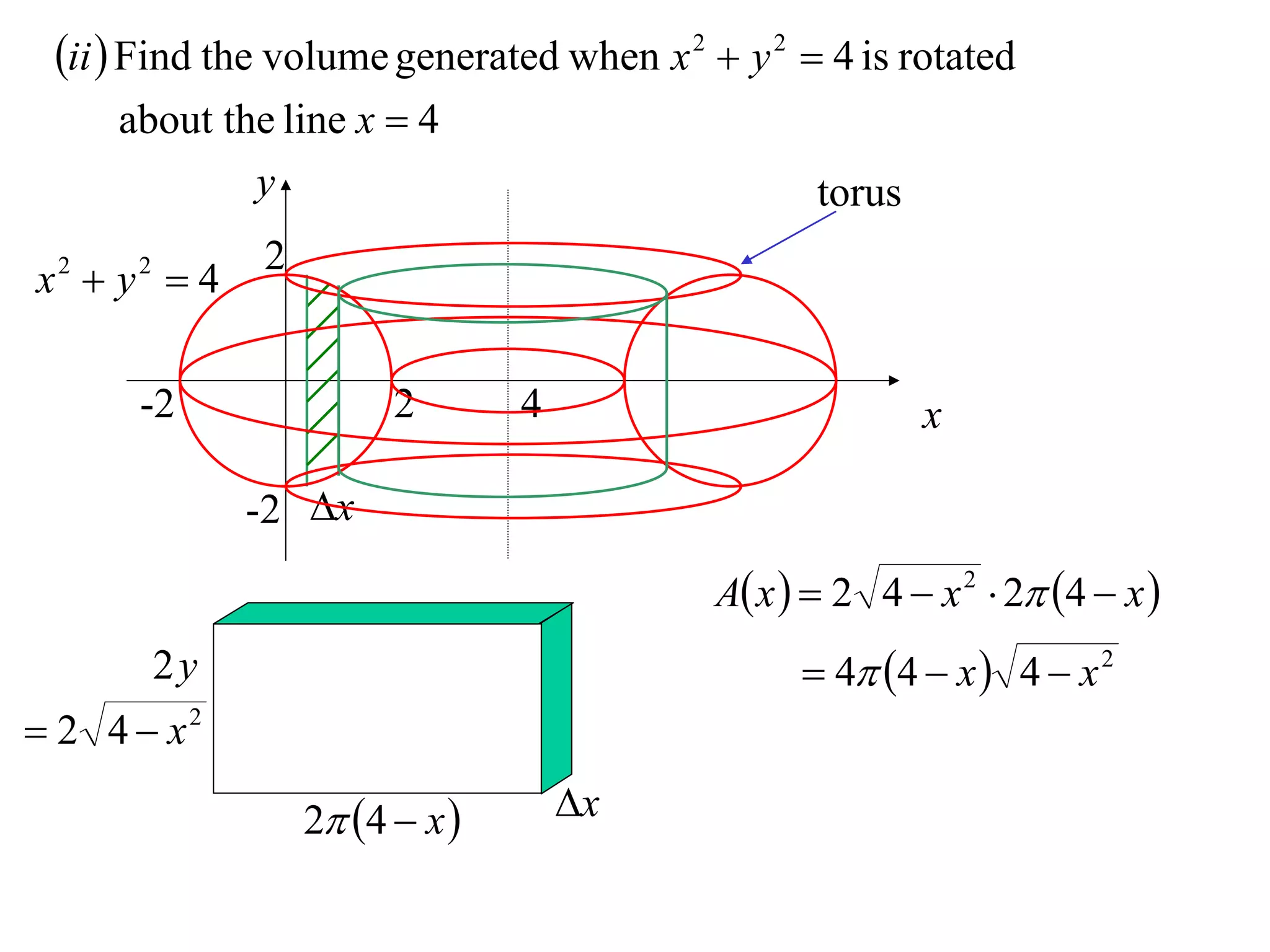
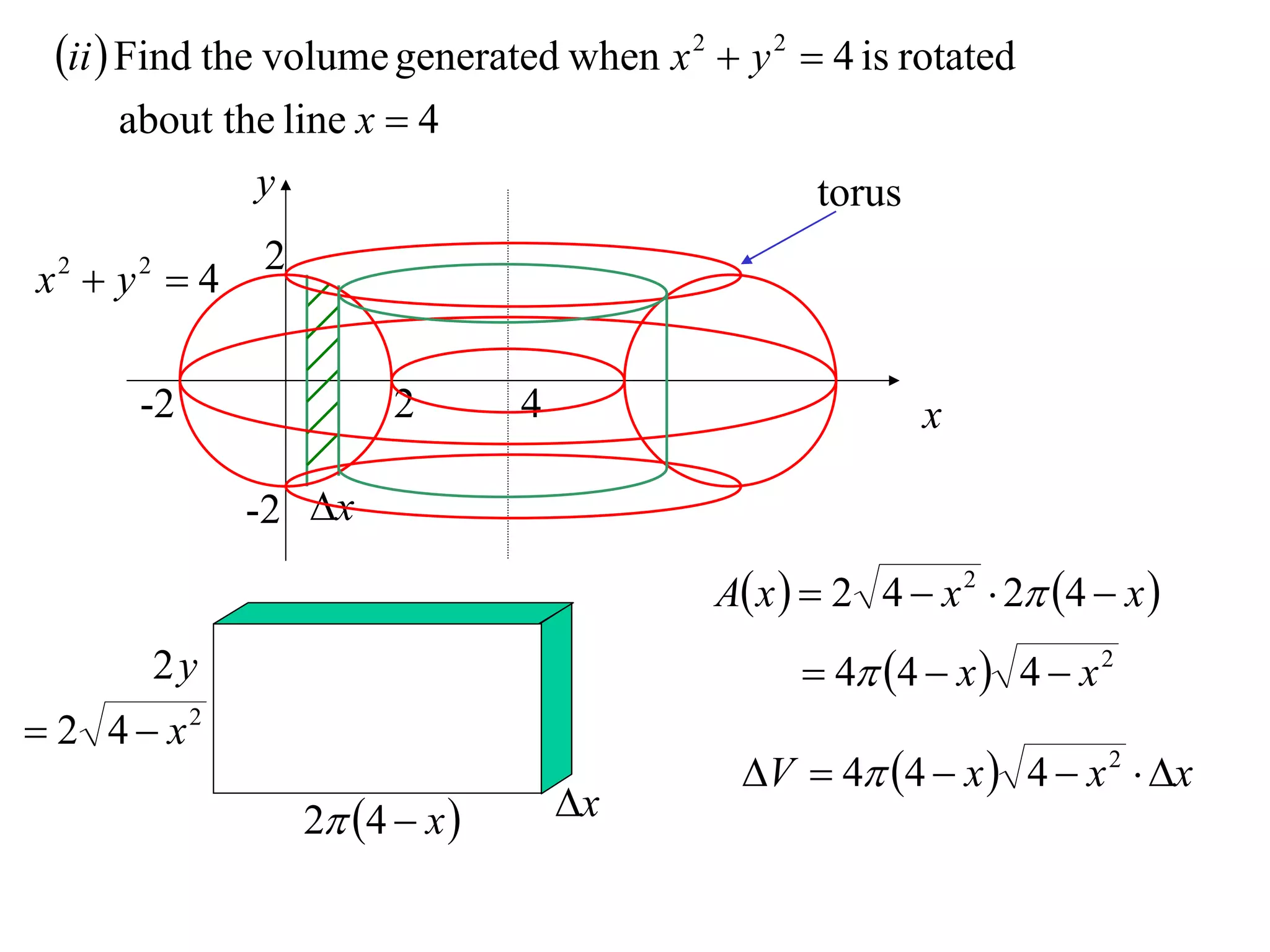
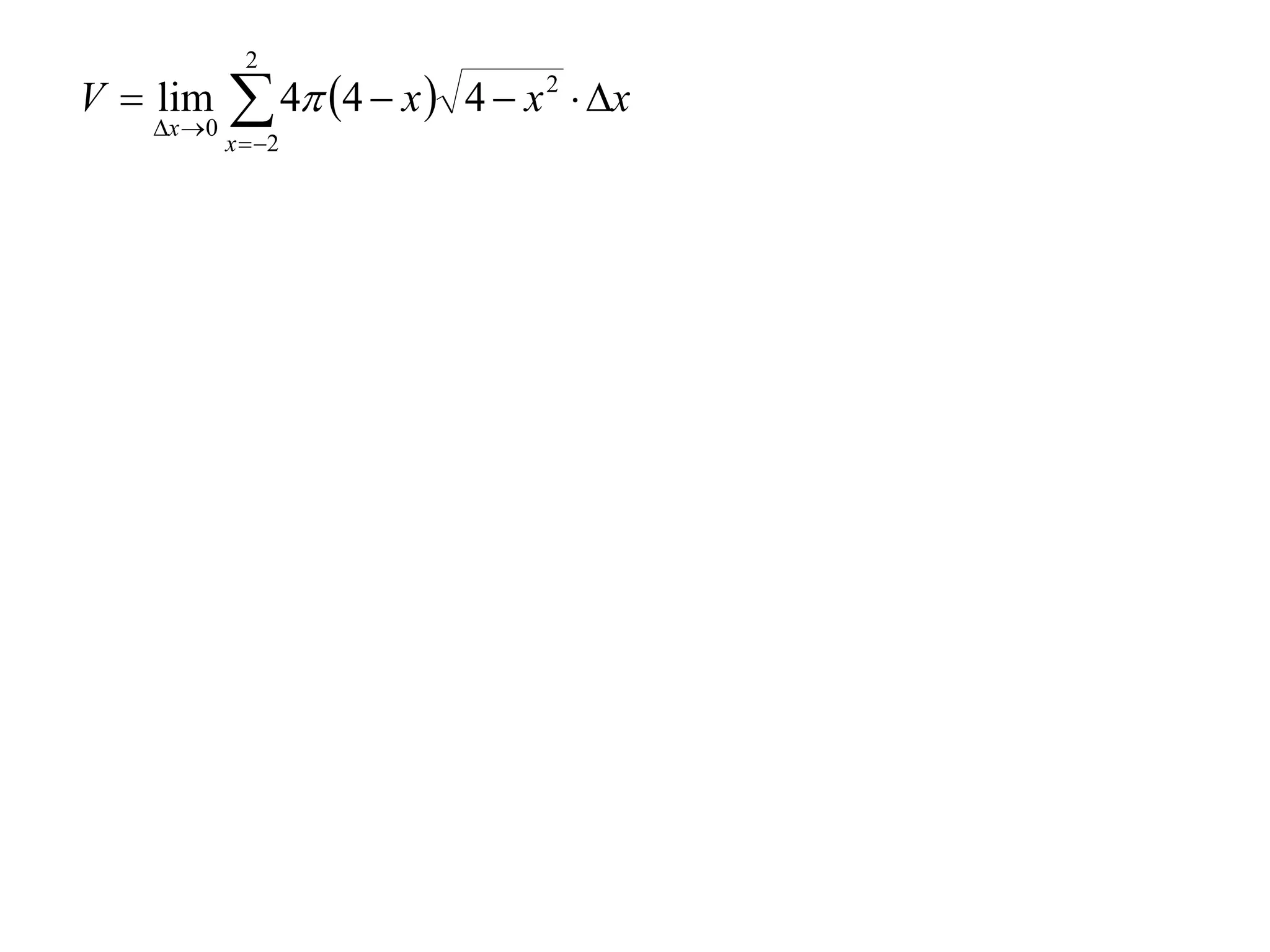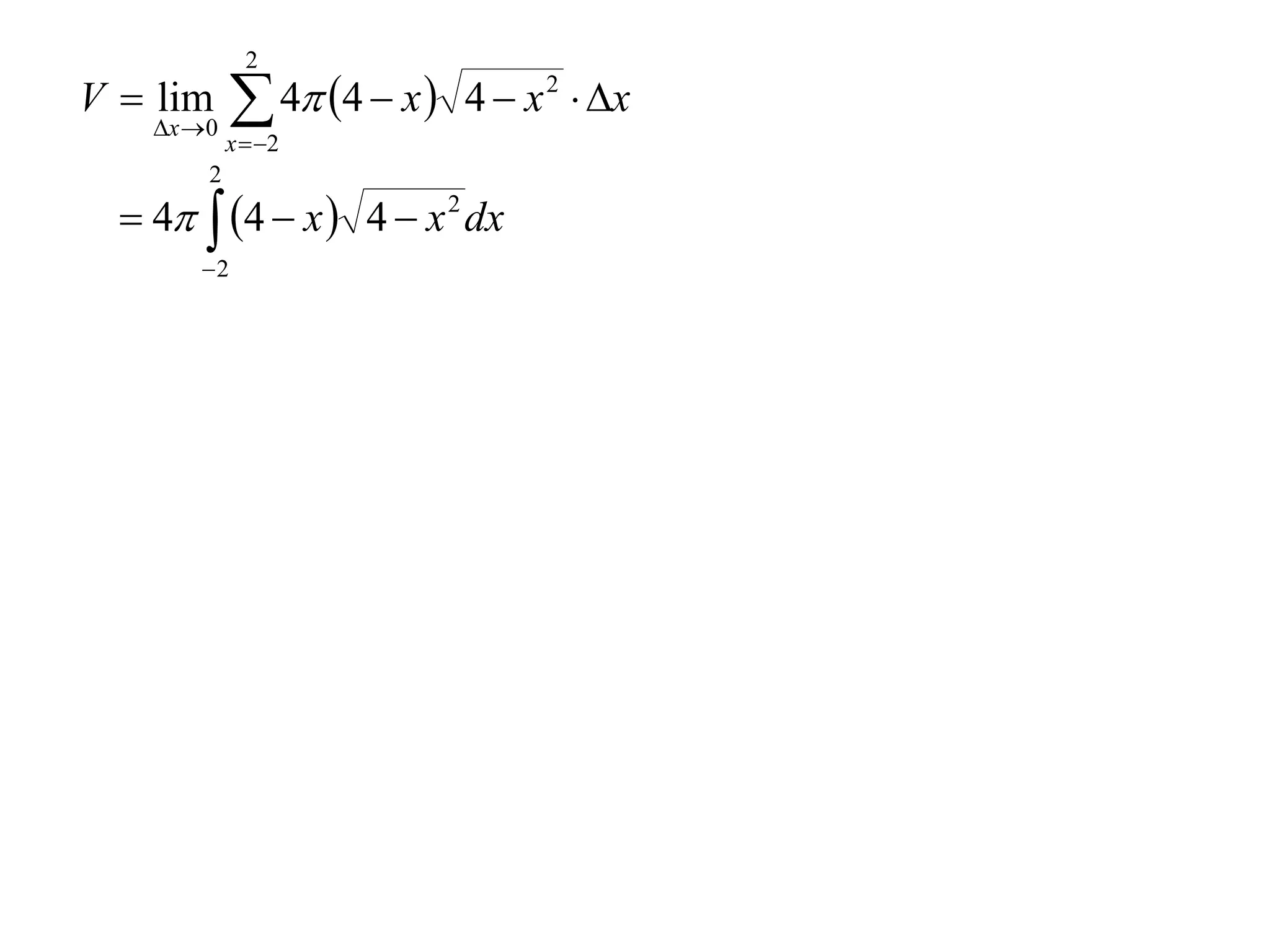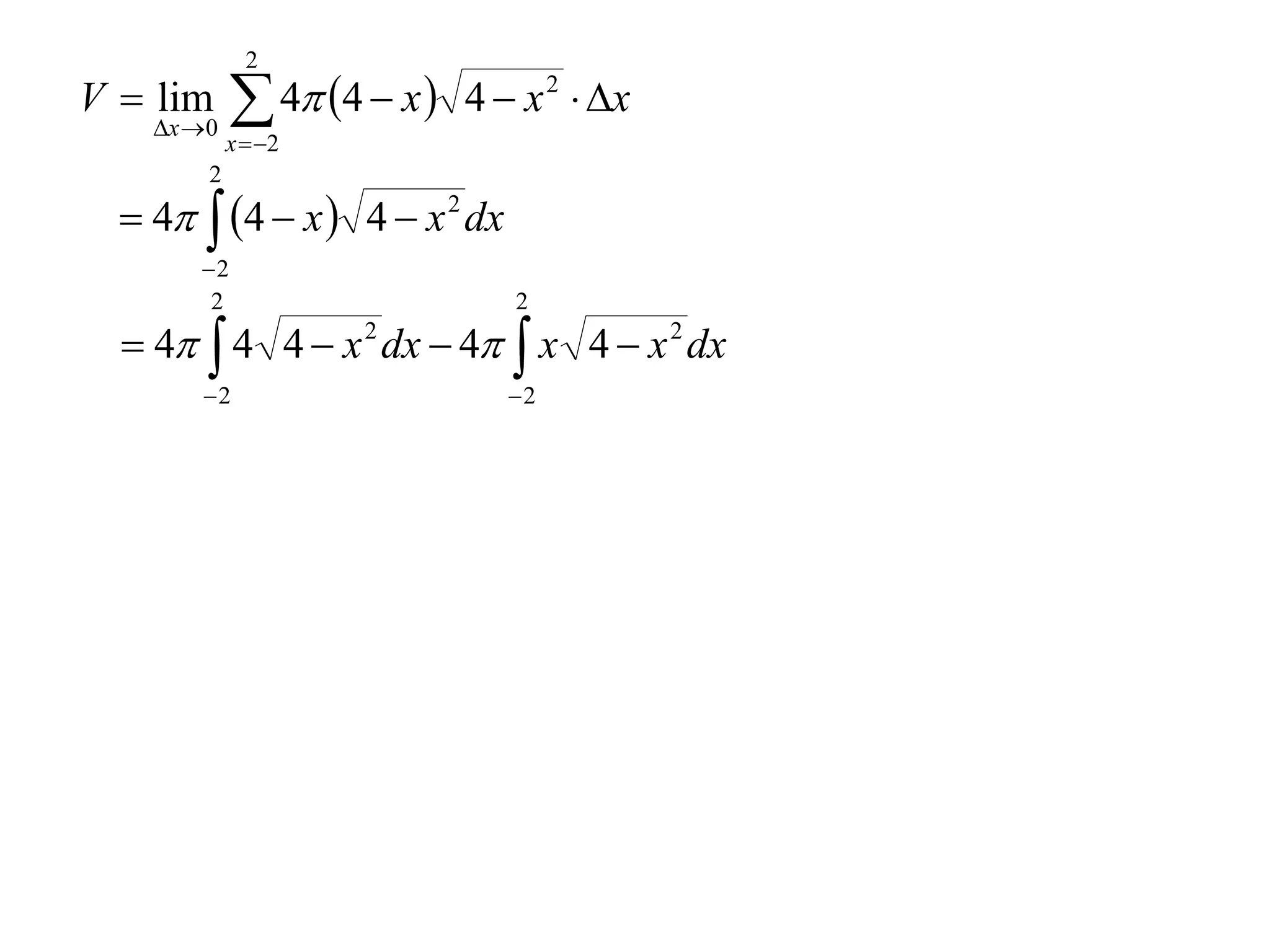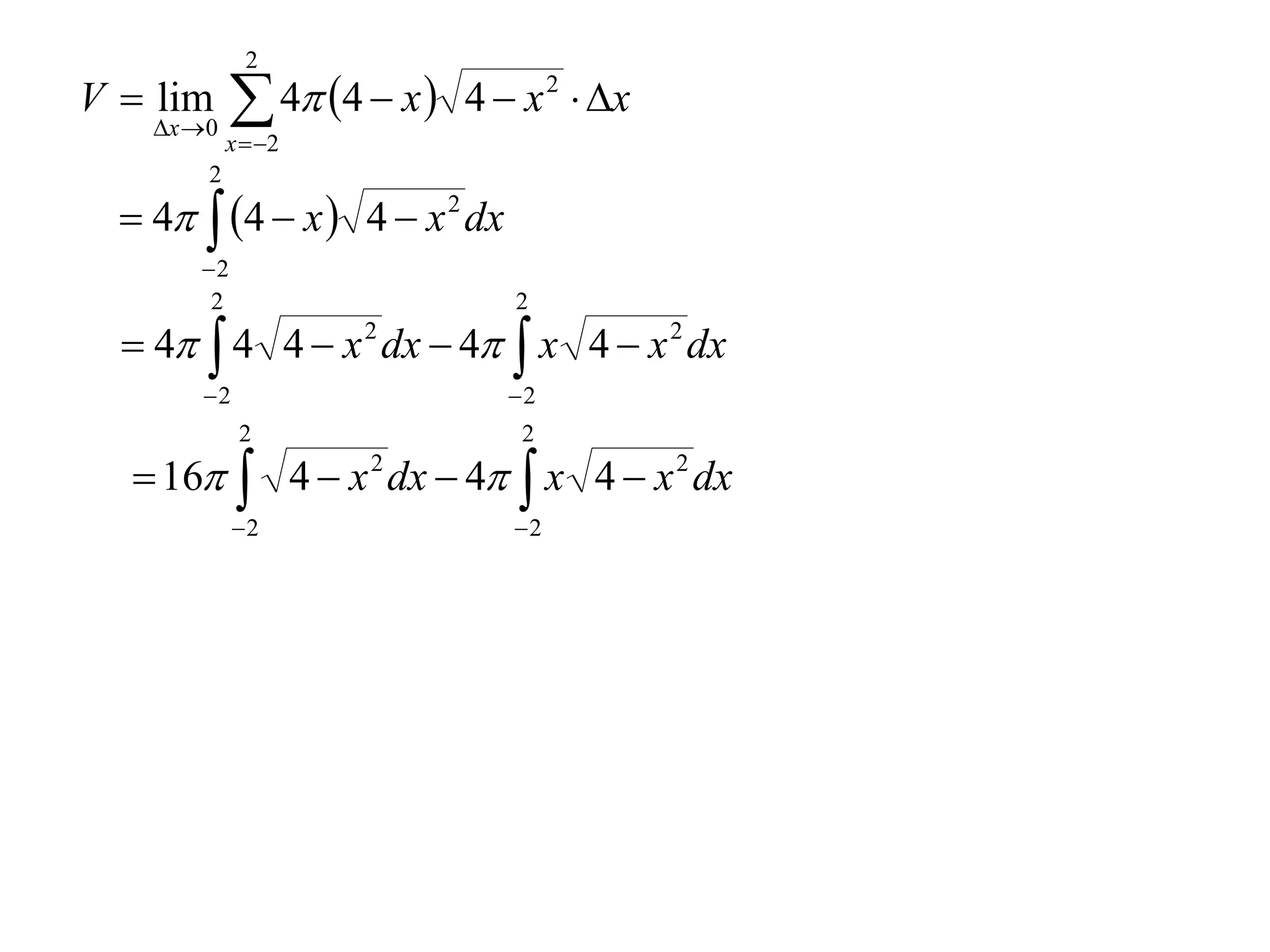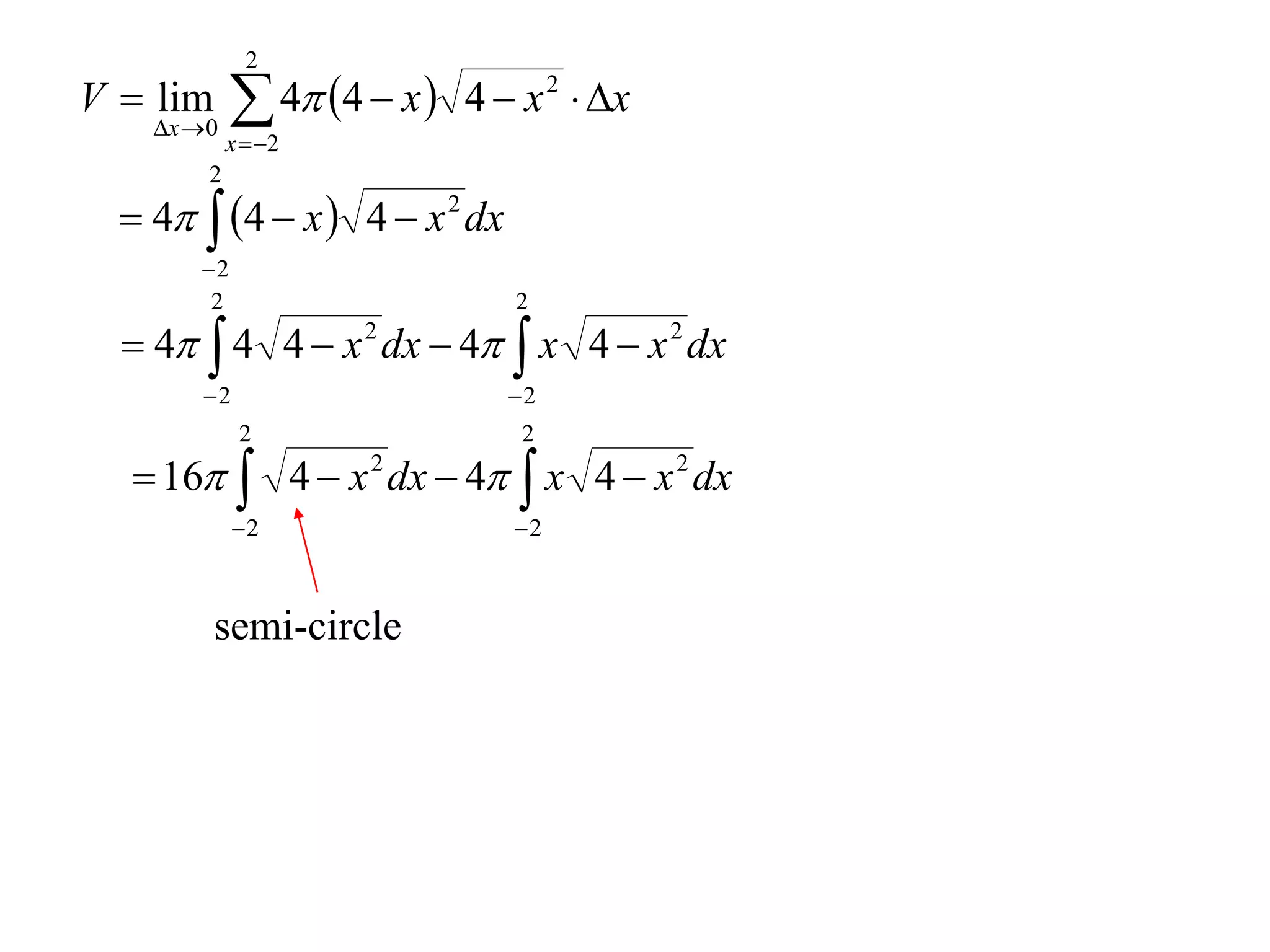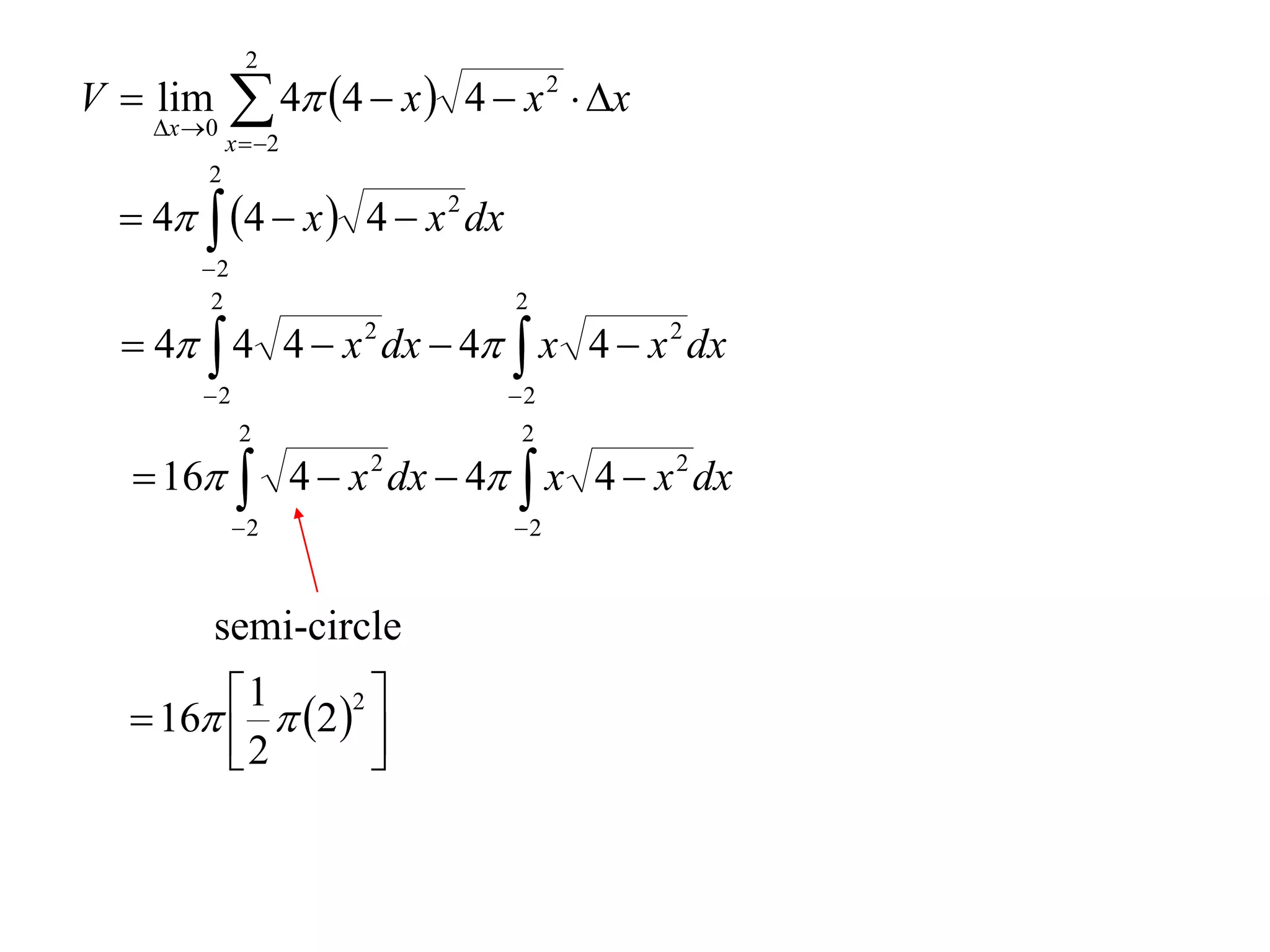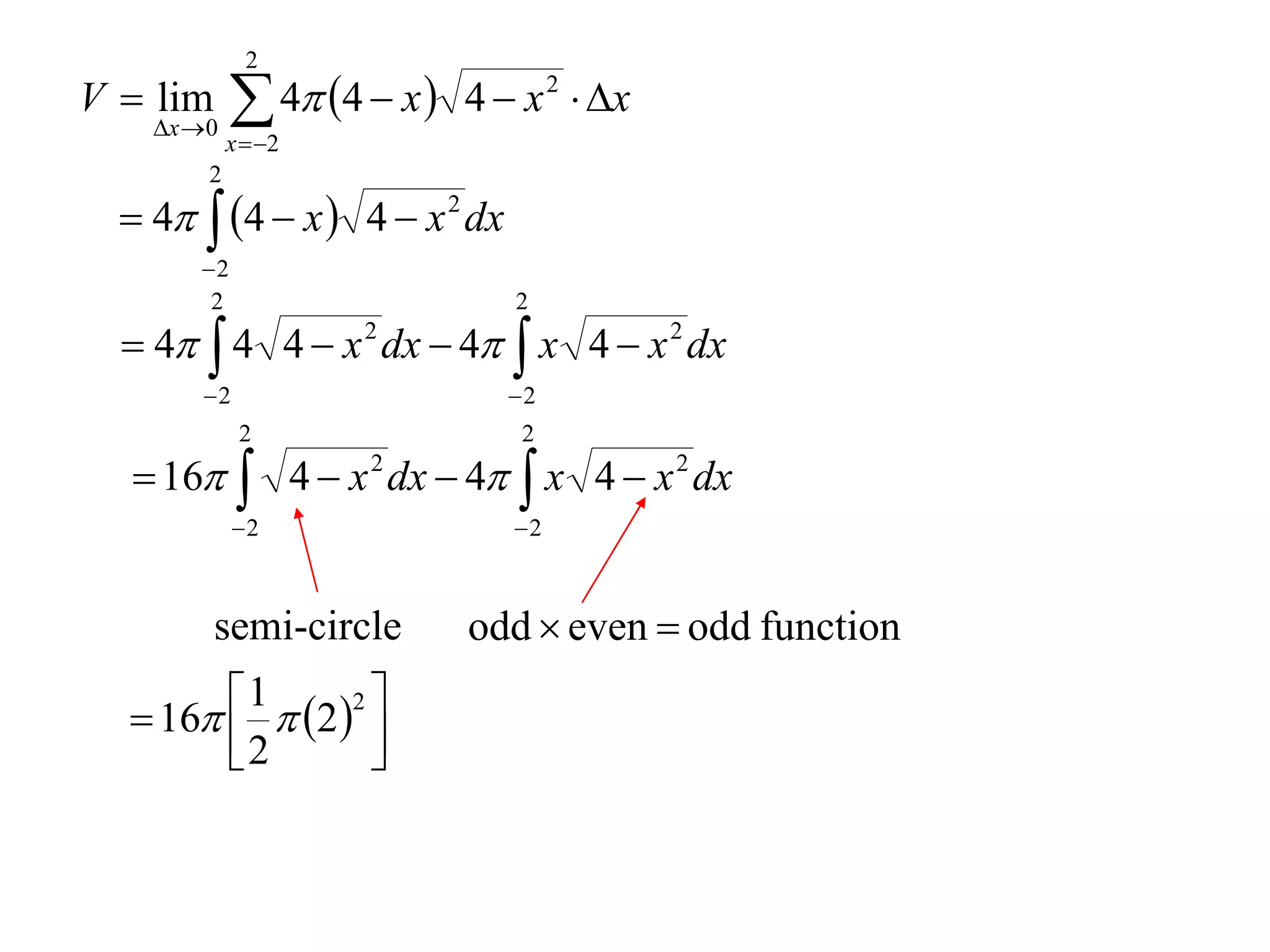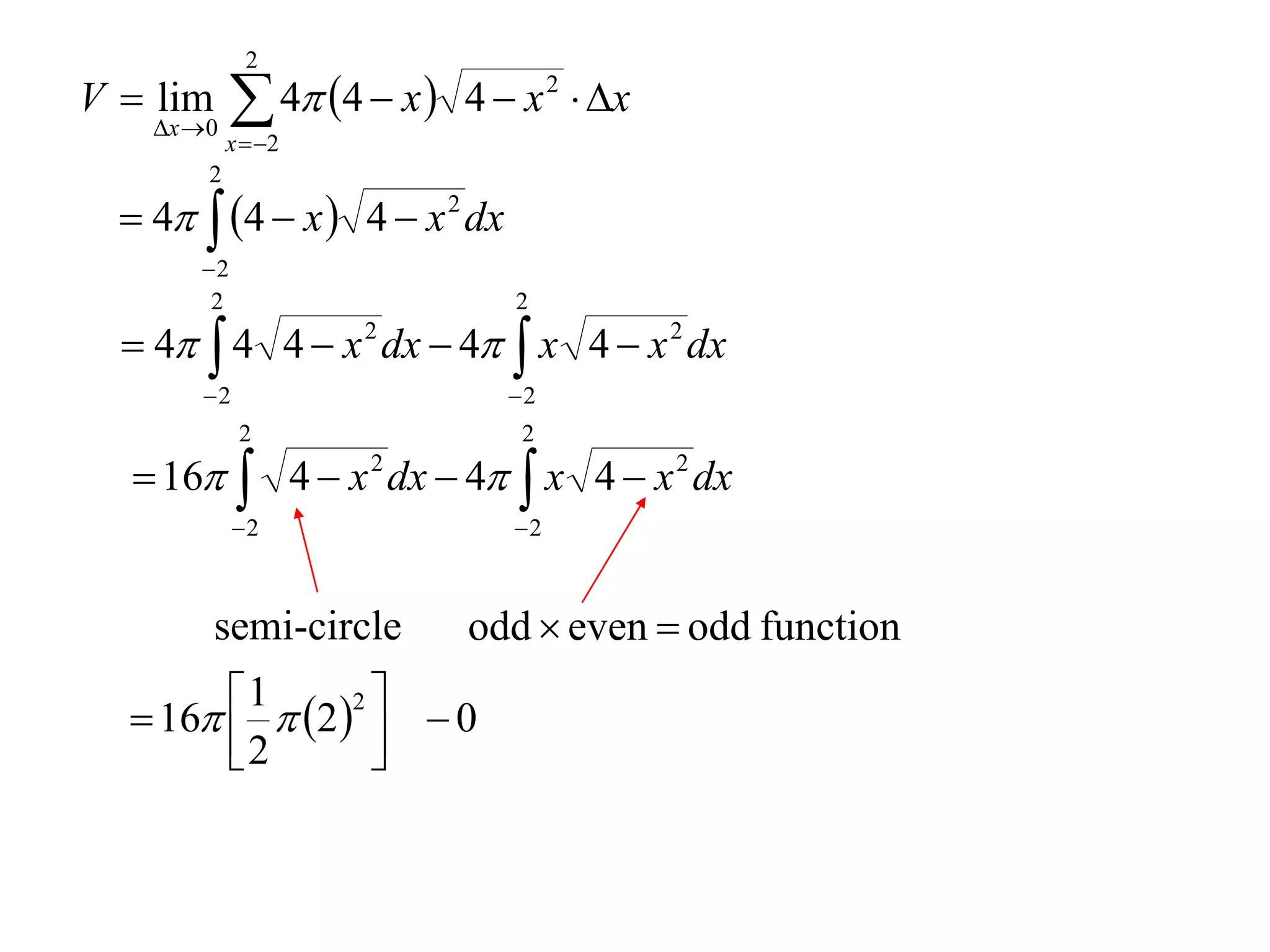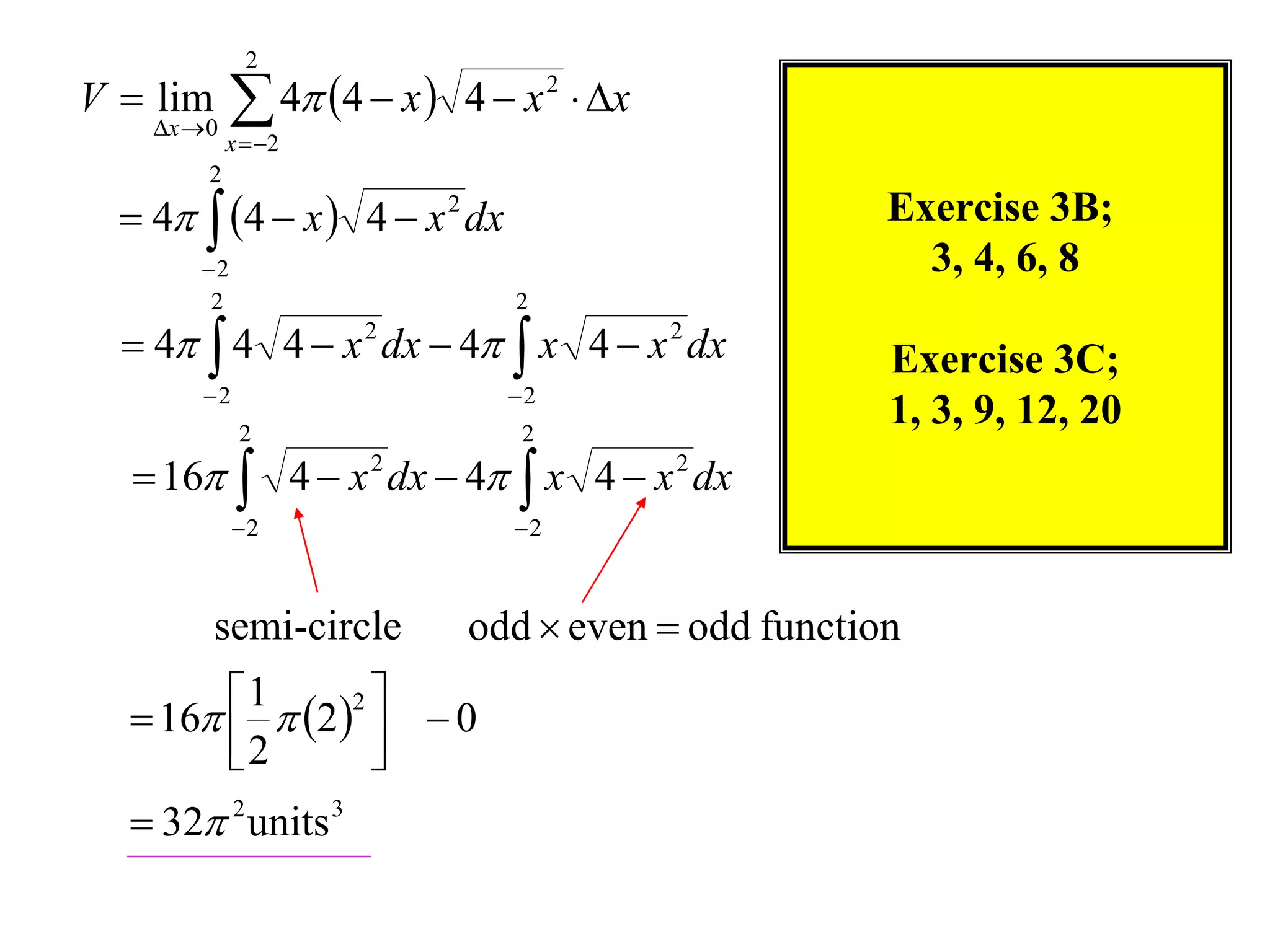The document discusses calculating volumes generated by rotating an area about an axis. It presents the method of cylindrical shells, which involves slicing the solid into thin cylindrical shells and summing their volumes. As an example, it calculates the volume generated by rotating the area between the parabola y = 4 - x^2 and the x-axis about the x-axis using cylindrical shells.

1. Volumes By Cylindrical Shells
slice || rotation 

2. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
x

3. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
a b x

4. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
a x b x

5. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
a x b x

6. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
a x b x

7. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
a x b x
x

8. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
y
a x b x
x

9. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
y  f x
a x b x
x

10. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
y  f x
a x b x
2x x

11. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
y  f x
a x b x
2x x
A x   2x  f  x 

12. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
y  f x
a x b x
2x x
A x   2x  f  x 
V  2x  f  x   x

13. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
y  f x
a x b x
2x x
A x   2x  f  x 
V  2x  f  x   x
b
V  lim  2x  f  x   x
x 0
xa

14. Volumes By Cylindrical Shells
slice || rotation 
y  f x
y
y  f x
a x b x
2x x
A x   2x  f  x 
V  2x  f  x   x
b
V  lim  2x  f  x   x
x 0
xa
b
 2  xf  x dx
a

15. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis

16. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2
-2 2 x

17. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2
y
-2 2 x

18. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2
y
-2 2 x

19. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2
y
-2 2 x
y

20. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2 1
y  x  4  y  2
-2 2 x
y
2x

21. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2 1
y  x  4  y  2
-2 2 x
y
2x

22. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2 1
y  x  4  y  2
-2 2 x
y
1
2 x  24  y  2

23. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2 1
y  x  4  y  2
-2 2 x
y
2y
1
2 x  24  y  2

24. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2 1
y  x  4  y  2
-2 2 x
y
A y   2y 24  y 1 
 
2
 
2y
1
2 x  24  y  2

25. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis
y
4
y  4  x2 1
y  x  4  y  2
-2 2 x
y
A y   2y 24  y 1 
 
2
 
1
2y V  4y 4  y 2  y
1
2 x  24  y  2

26. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis 4 1
V  lim  4y 4  y 2  y
y y 0
x 0
4
y  4  x2 1
y  x  4  y  2
-2 2 x
y
A y   2y 24  y 1 
 
2
 
1
2y V  4y 4  y 2  y
1
2 x  24  y  2

27. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis 4 1
V  lim  4y 4  y 2  y
y y 0
x 0
4
y  4 x 2 4 1
y
1
 x  4  y  2  4  y 4  y 2 dy
0
-2 2 x
y
A y   2y 24  y 1 
 
2
 
1
2y V  4y 4  y 2  y
1
2 x  24  y  2

28. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis 4 1
V  lim  4y 4  y 2  y
y y 0
x 0
4
y  4 x 2 4 1
y
1
 x  4  y  2  4  y 4  y 2 dy
0
4 1
-2 2 x  4  4  y  y dy
2
0
y
A y   2y 24  y 1 
 
2
 
1
2y V  4y 4  y 2  y
1
2 x  24  y  2

29. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis 4 1
V  lim  4y 4  y 2  y
y y 0
x 0
4
y  4 x 2 4 1
y
1
 x  4  y  2  4  y 4  y 2 dy
0
4 1
-2 2 x  4  4  y  y dy
2
0
y
4
 1 3

 4   4 y  y dy

2 2
24  y 1  0 
A y   2y
 
2
 
1
2y V  4y 4  y 2  y
1
2 x  24  y  2

30. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis 4 1
V  lim  4y 4  y 2  y
y y 0
x 0
4
y  4 x 2 4 1
y
1
 x  4  y  2  4  y 4  y 2 dy
0
4 1
-2 2 x  4  4  y  y dy
2
0
y
4
 1 3

 4   4 y  y dy

2 2
24  y 1  0 
A y   2y 5 4
 
2
  8 2 2 2 
3
1  4  y  y 
2y V  4y 4  y 2  y 3 5 0
1
2 x  24  y  2

31. e.g. i  Find the volume generated when the area between y  4  x 2 and
the x axis is rotated about the x axis 4 1
V  lim  4y 4  y 2  y
y y 0
x 0
4
y  4 x 2 4 1
y
1
 x  4  y  2  4  y 4  y 2 dy
0
4 1
-2 2 x  4  4  y  y dy
2
0
y
4
 1 3

 4   4 y  y dy

2 2
24  y 1  0 
A y   2y 5 4
 
2
  8 2 2 2 
3
1  4  y  y 
2y V  4y 4  y 2  y 3 5 0
8    2 32   0
 4  8 
 3 5 
512

1
2 x  24  y  2
15
units 3

32. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4

33. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y
2
x2  y2  4
-2 2 x
-2

34. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y
2
x2  y2  4
-2 2 4 x
-2

35. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y
2
x2  y2  4
-2 2 4 x
-2 x

36. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y
2
x2  y2  4
-2 2 4 x
-2 x

37. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y
2
x2  y2  4
-2 2 4 x
-2 x

38. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x

39. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x

40. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x
x

41. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x
2y
x

42. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x
2y
 2 4  x2
x

43. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x
2y
 2 4  x2
2 4  x  x

44. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x
A x   2 4  x 2  2 4  x 
2y
 2 4  x2
2 4  x  x

45. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x
A x   2 4  x 2  2 4  x 
2y  4 4  x  4  x 2
 2 4  x2
2 4  x  x

46. ii  Find the volume generated when x 2  y 2  4 is rotated
about the line x  4
y torus
2
x2  y2  4
-2 2 4 x
-2 x
A x   2 4  x 2  2 4  x 
2y  4 4  x  4  x 2
 2 4  x2
V  4 4  x  4  x 2  x
2 4  x  x

47. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2

48. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2

49. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx
2 2

50. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx
2 2
2 2
 16  4  x 2 dx  4  x 4  x 2 dx
2 2

51. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx
2 2
2 2
 16  4  x 2 dx  4  x 4  x 2 dx
2 2
semi-circle

52. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx
2 2
2 2
 16  4  x 2 dx  4  x 4  x 2 dx
2 2
semi-circle
 1  2 2 
 16 
2 


53. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx
2 2
2 2
 16  4  x 2 dx  4  x 4  x 2 dx
2 2
semi-circle odd  even  odd function
 1  2 2 
 16 
2 


54. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx
2 2
2 2
 16  4  x 2 dx  4  x 4  x 2 dx
2 2
semi-circle odd  even  odd function
 1  2 2 
 16 
2  0


55. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx
2
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx
2 2
2 2
 16  4  x 2 dx  4  x 4  x 2 dx
2 2
semi-circle odd  even  odd function
 1  2 2 
 16 
2  0

 32 2 units 3

56. 2
V  lim
x  0
 4 4  x  4  x 2  x
x  2
2
 4  4  x  4  x 2 dx Exercise 3B;
2 3, 4, 6, 8
2 2
 4  4 4  x 2 dx  4  x 4  x 2 dx Exercise 3C;
2 2
2 2
1, 3, 9, 12, 20
 16  4  x 2 dx  4  x 4  x 2 dx
2 2
semi-circle odd  even  odd function
 1  2 2 
 16 
2  0

 32 2 units 3