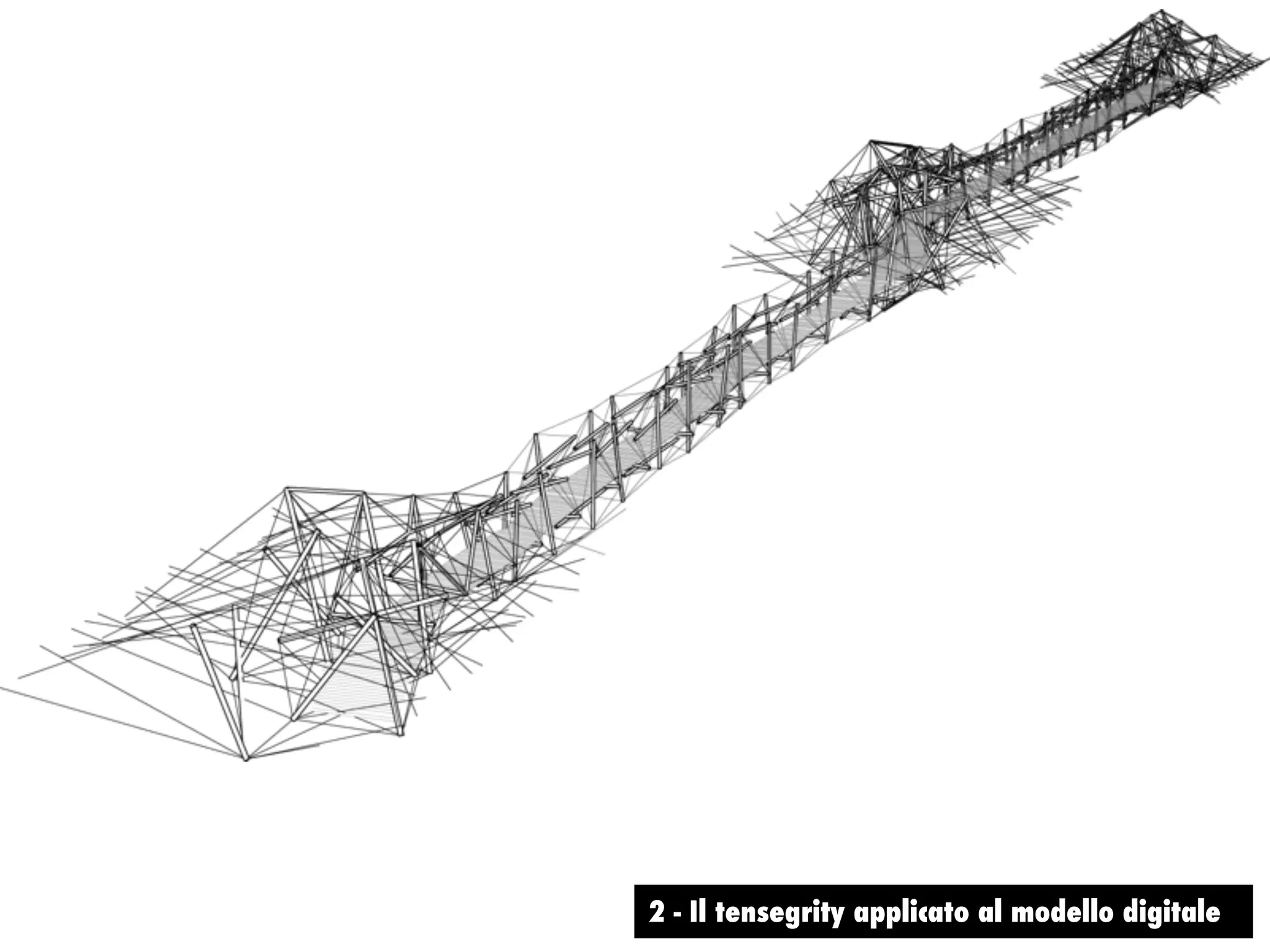
Il documento discute un progetto di passerella ciclabile sul fiume Sesia, esplorando le sue caratteristiche, il contesto locale e le figure coinvolte. Si evidenzia l'importanza della progettazione di strutture tensegrity e la morfogenesi necessaria per garantire stabilità e funzionalità. Inoltre, viene analizzato il dimensionamento e le verifiche strutturali legate ai materiali utilizzati nel progetto.