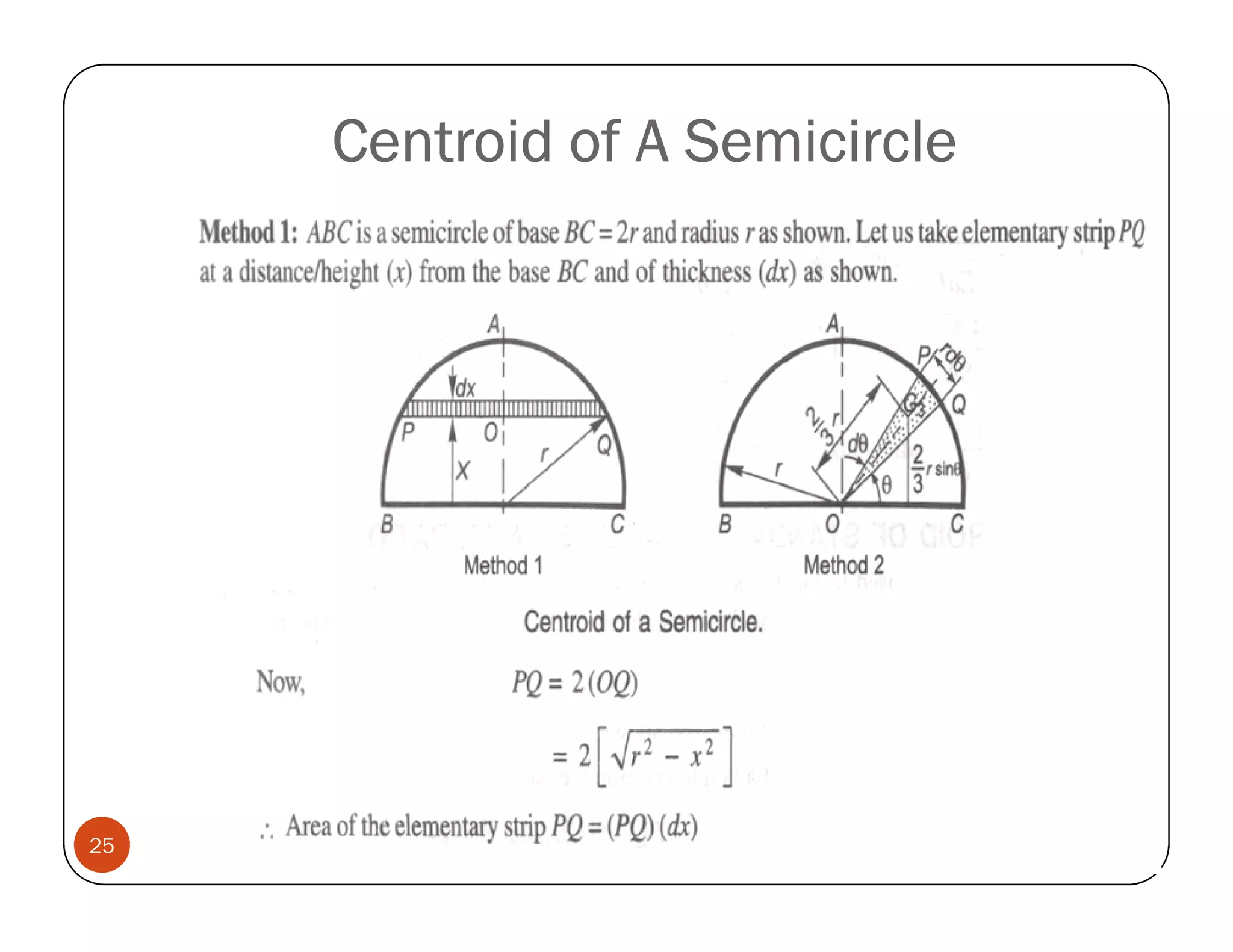
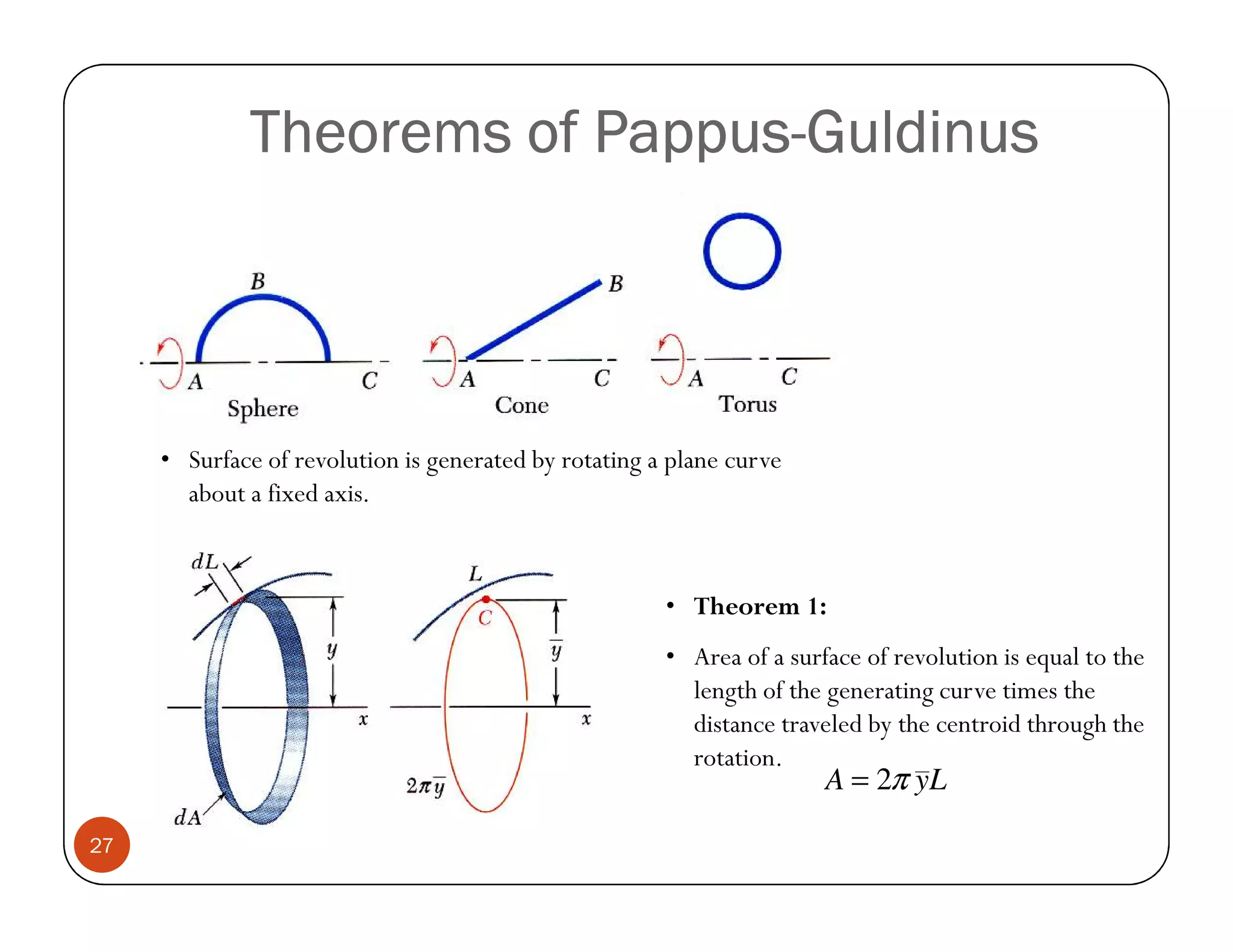
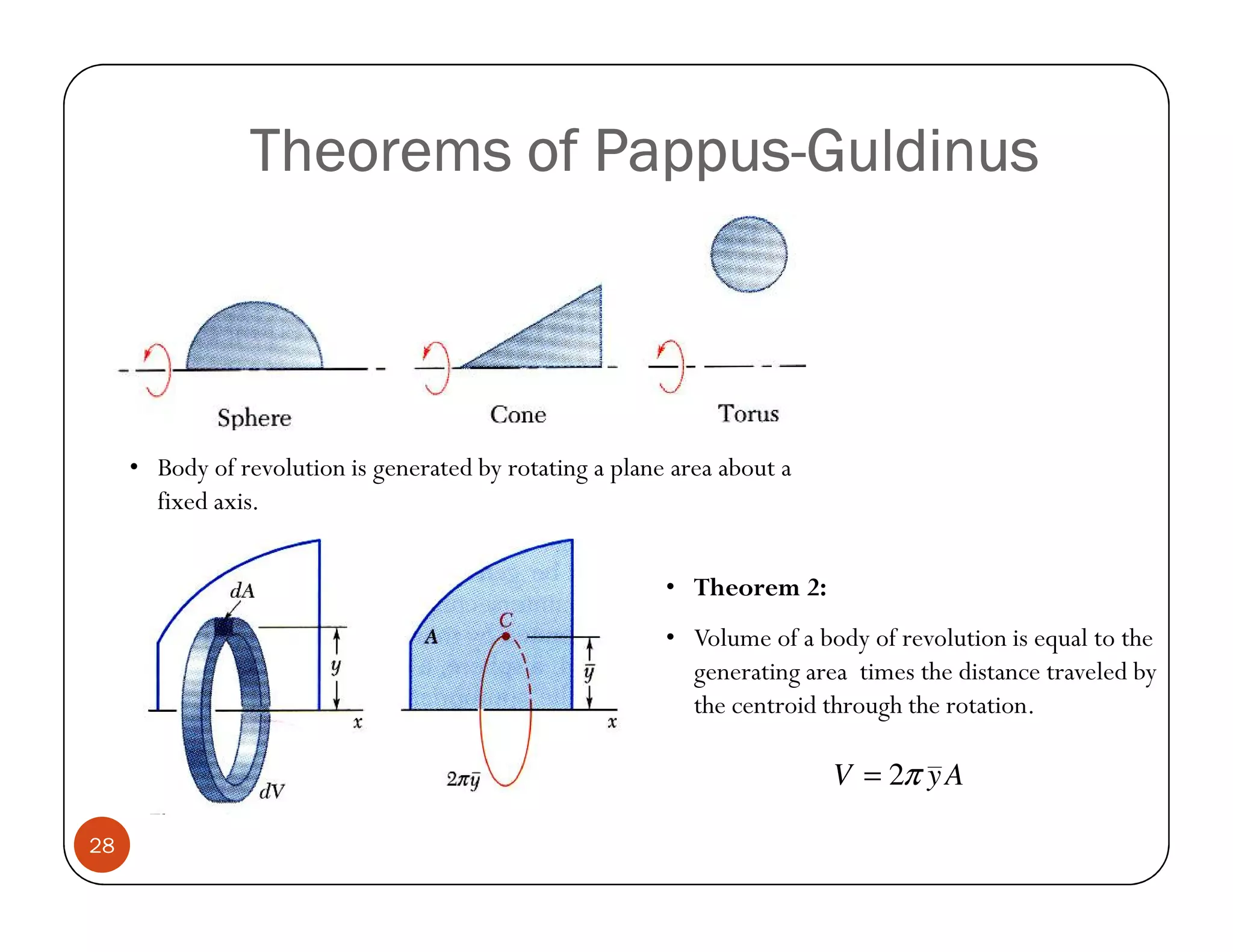
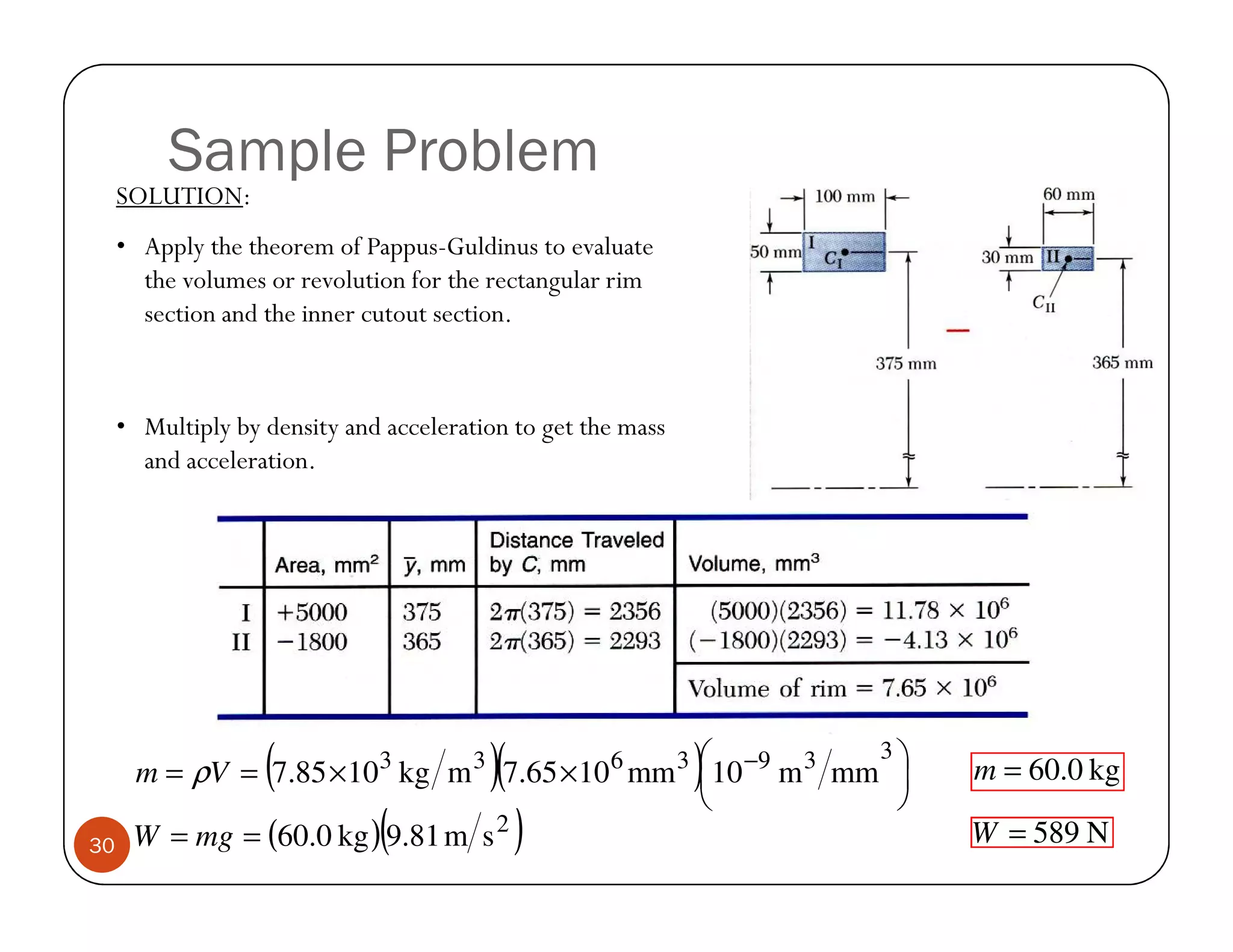
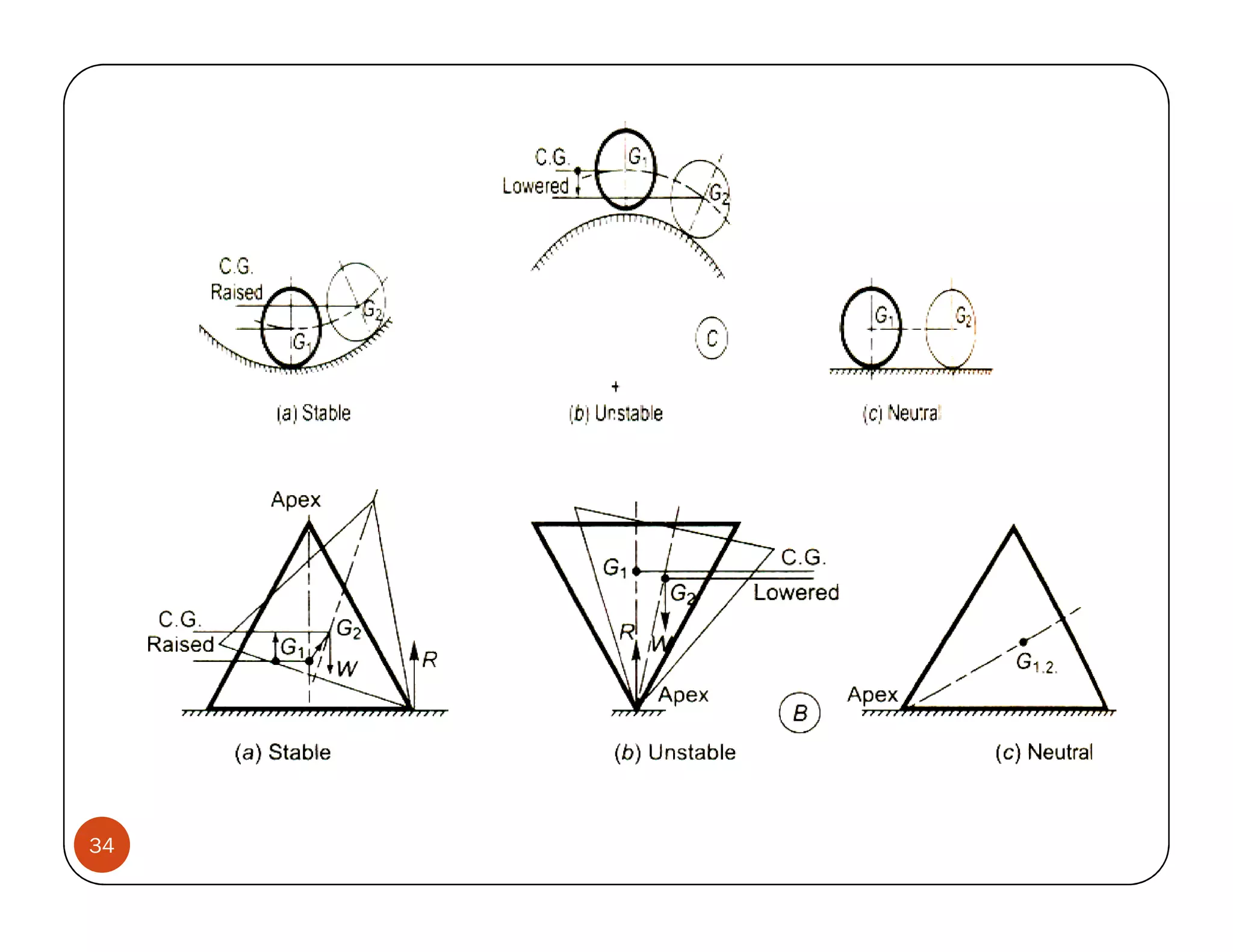
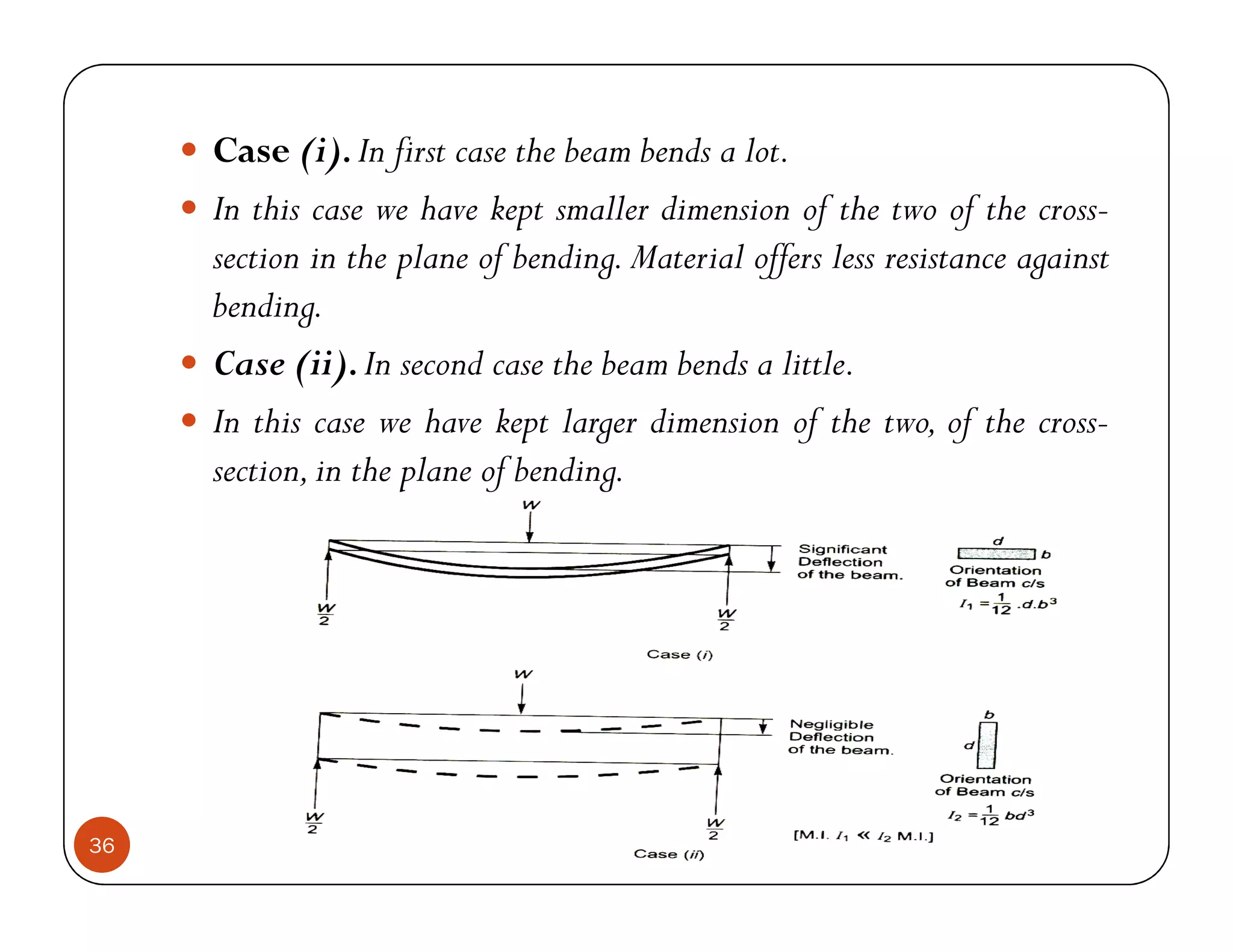
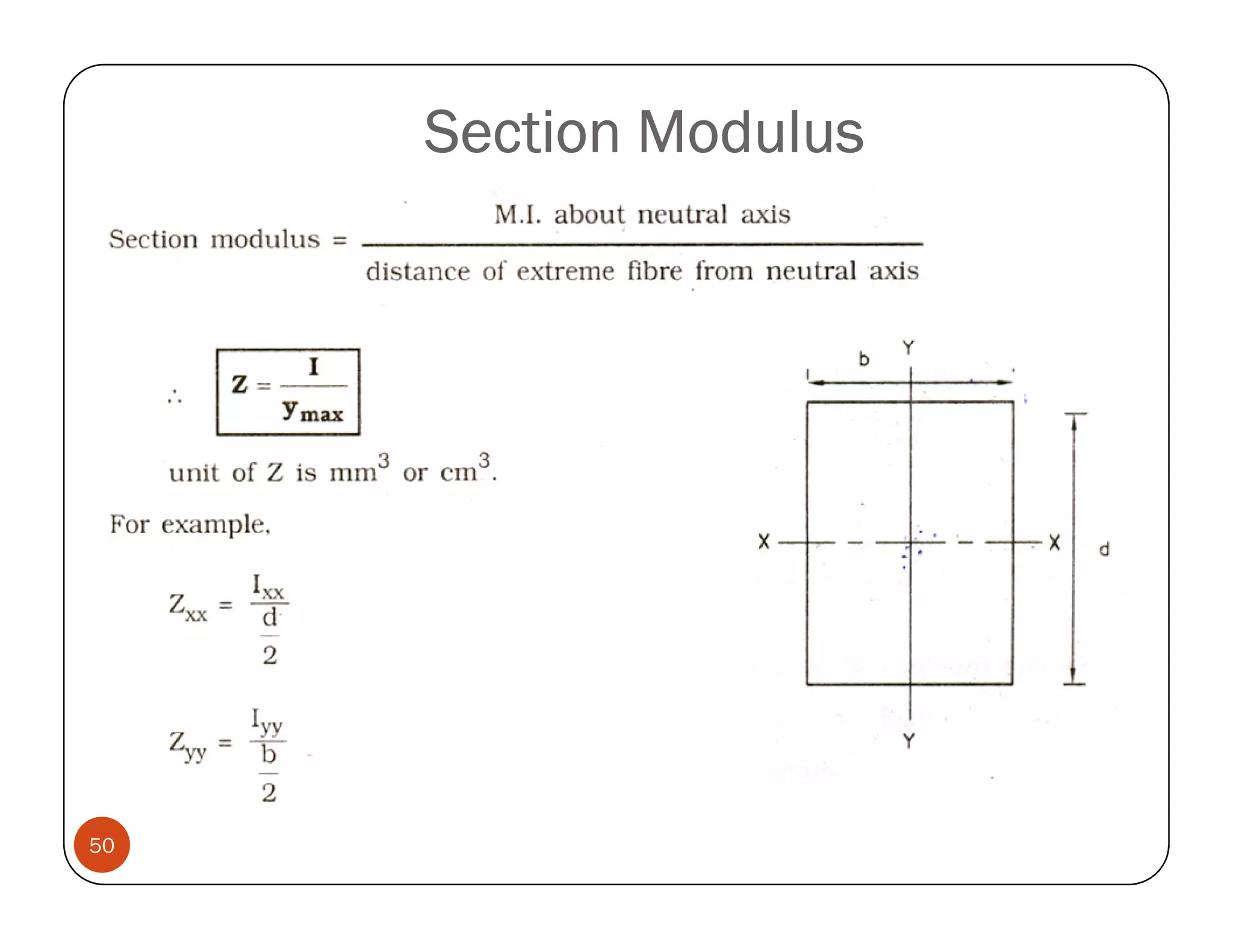
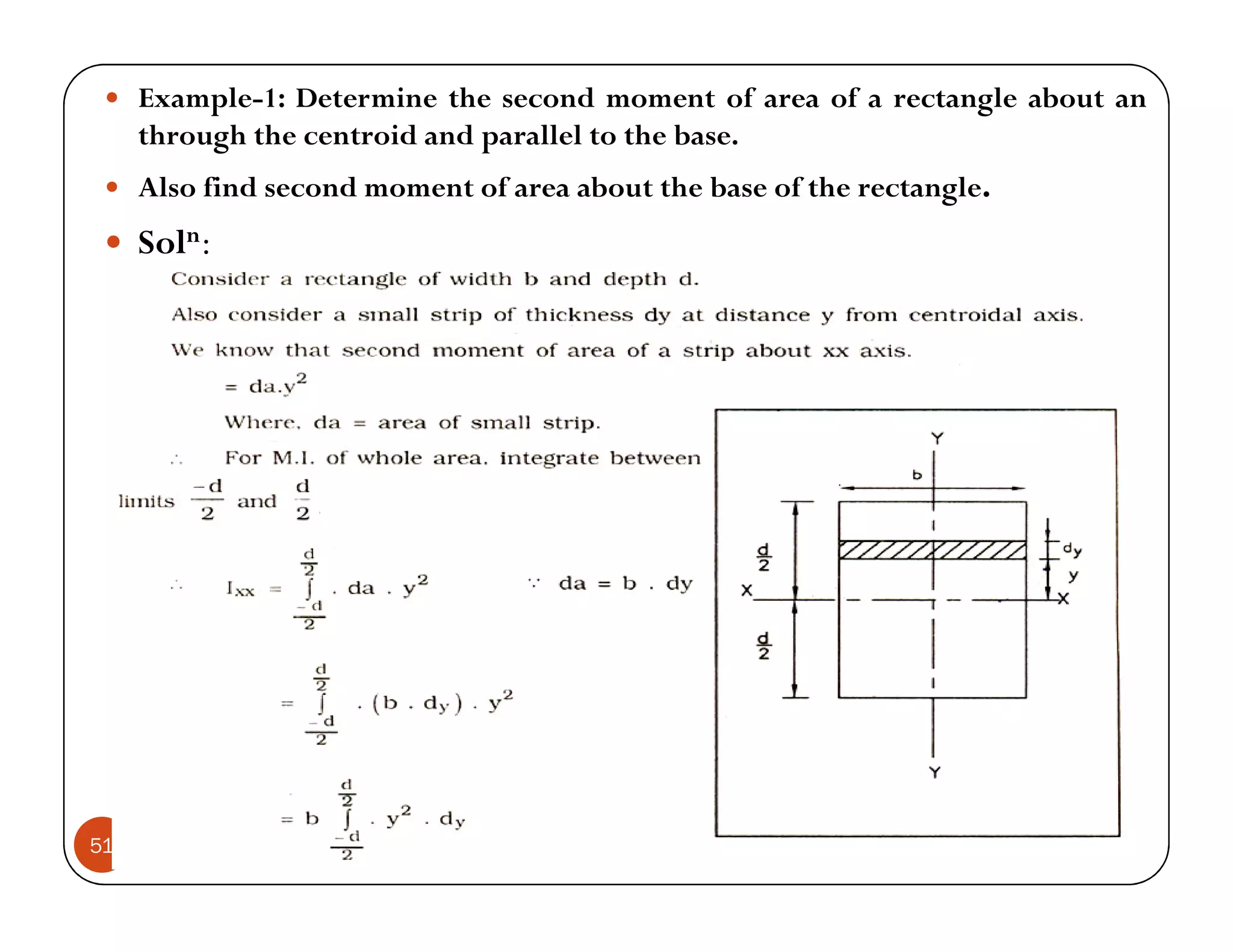
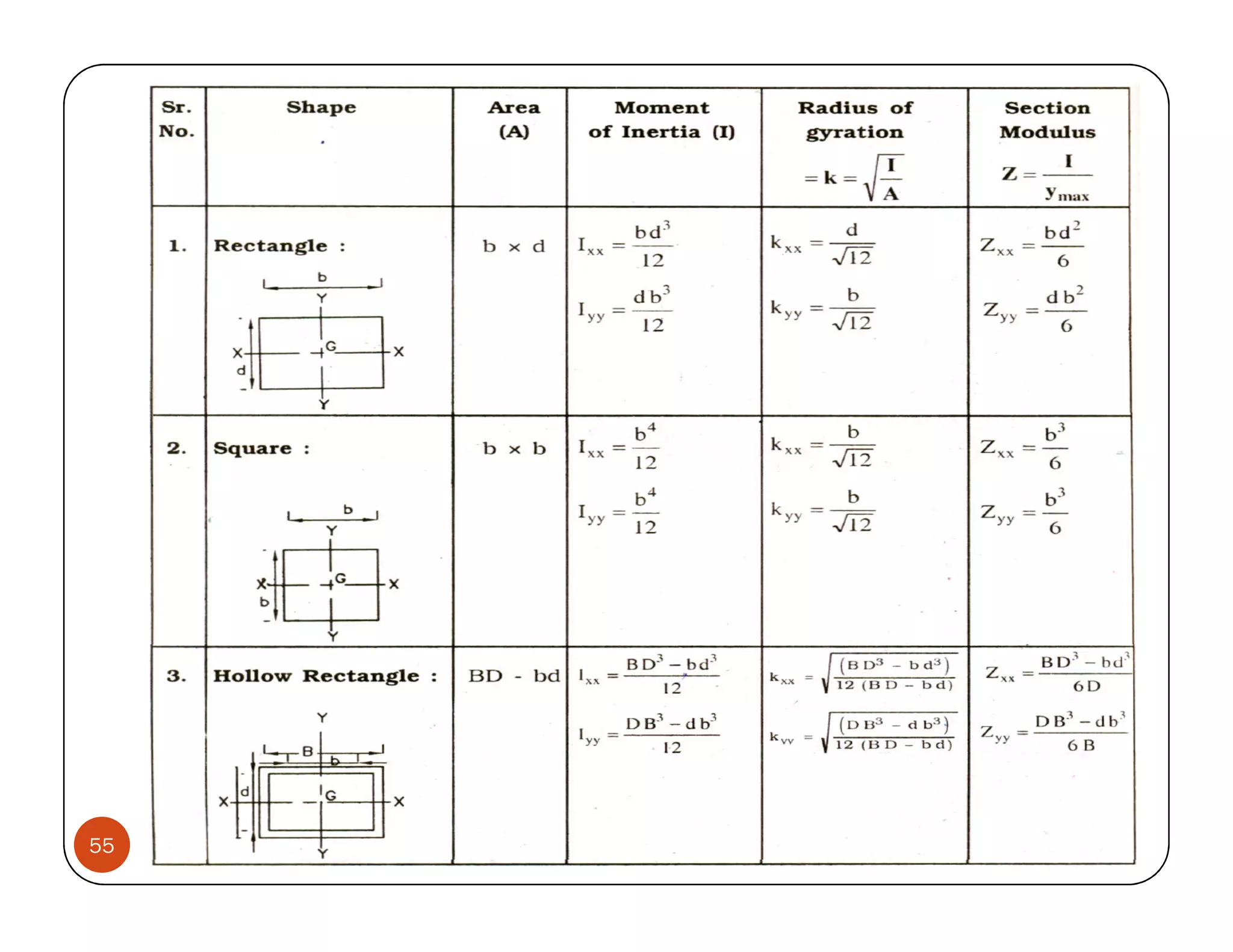
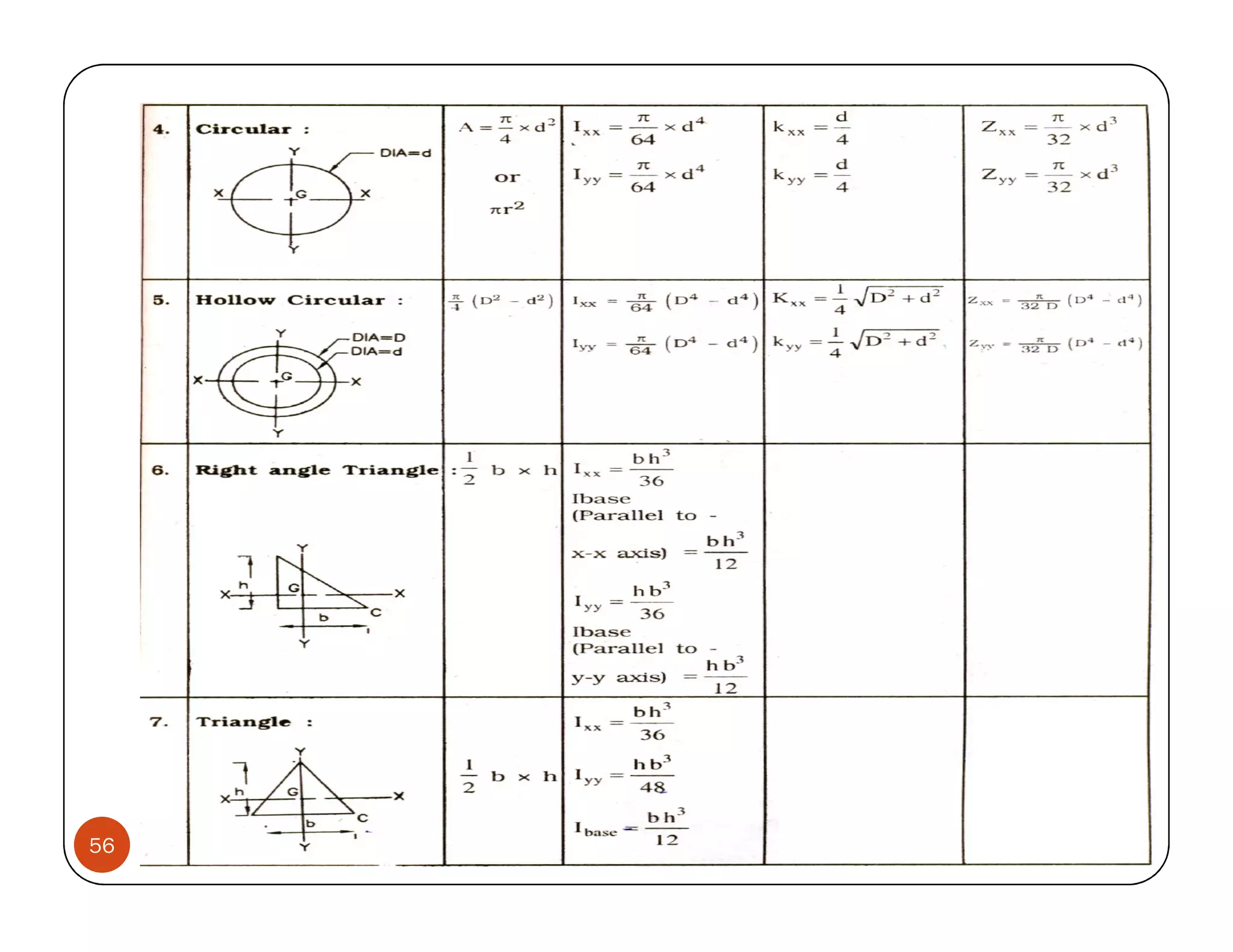
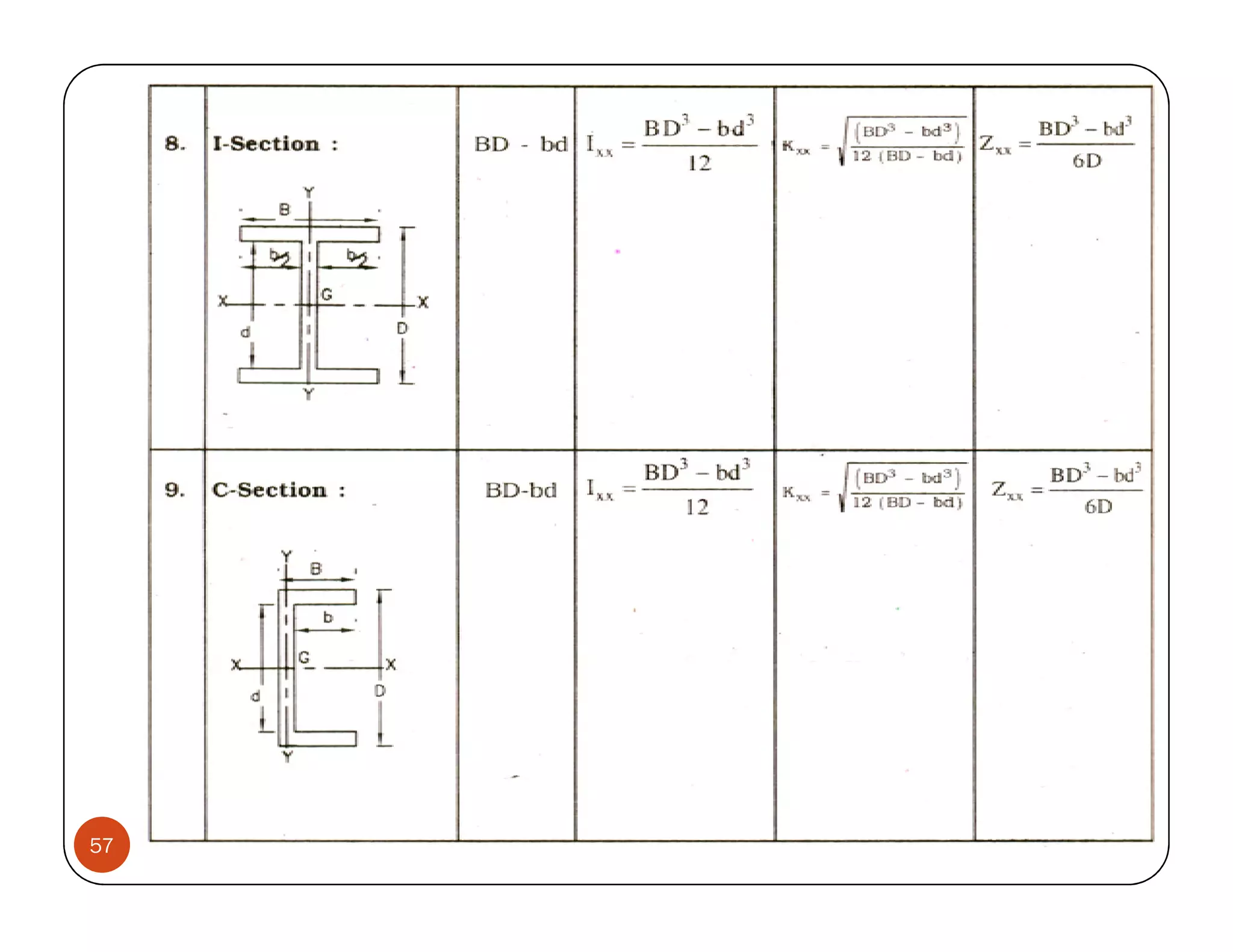
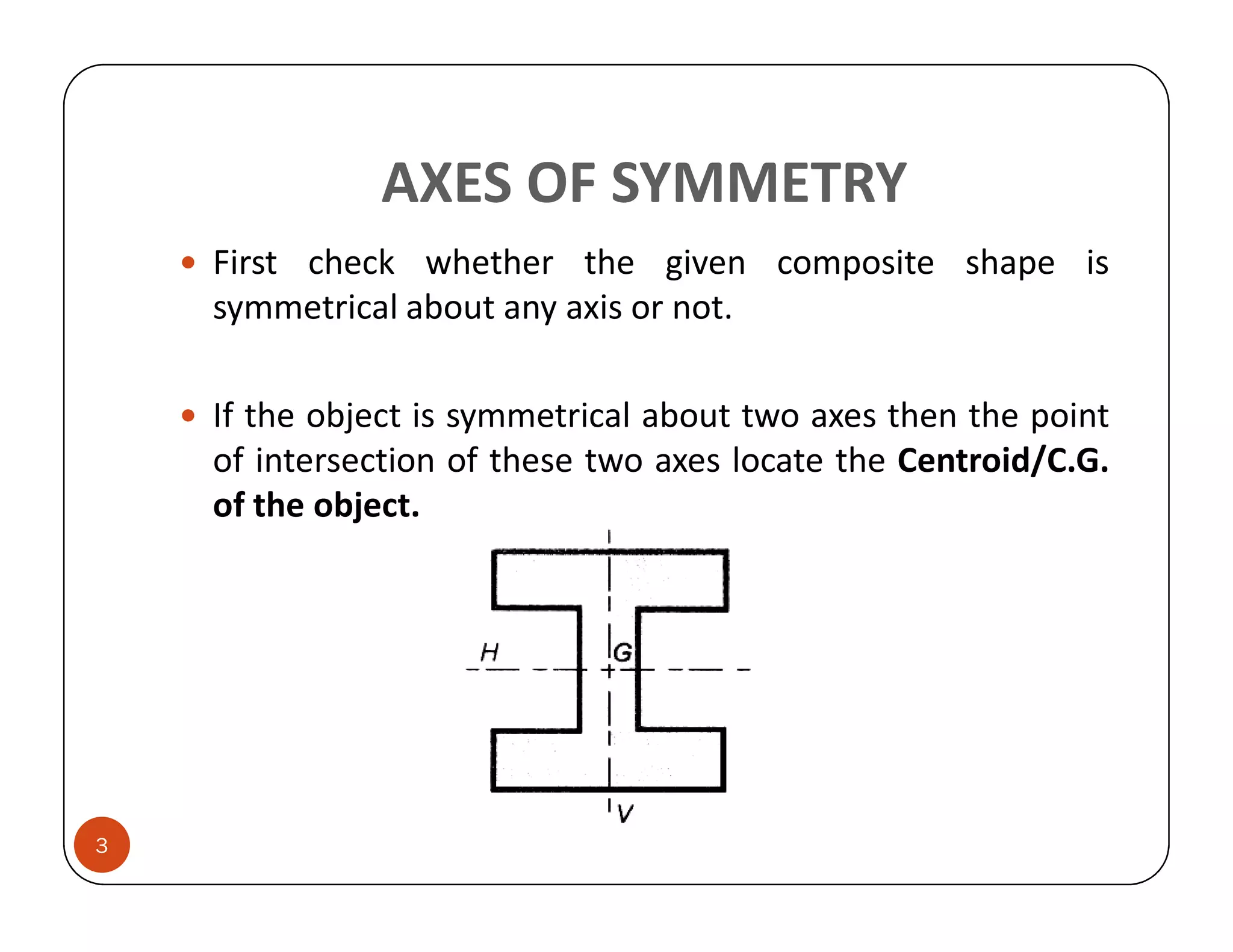
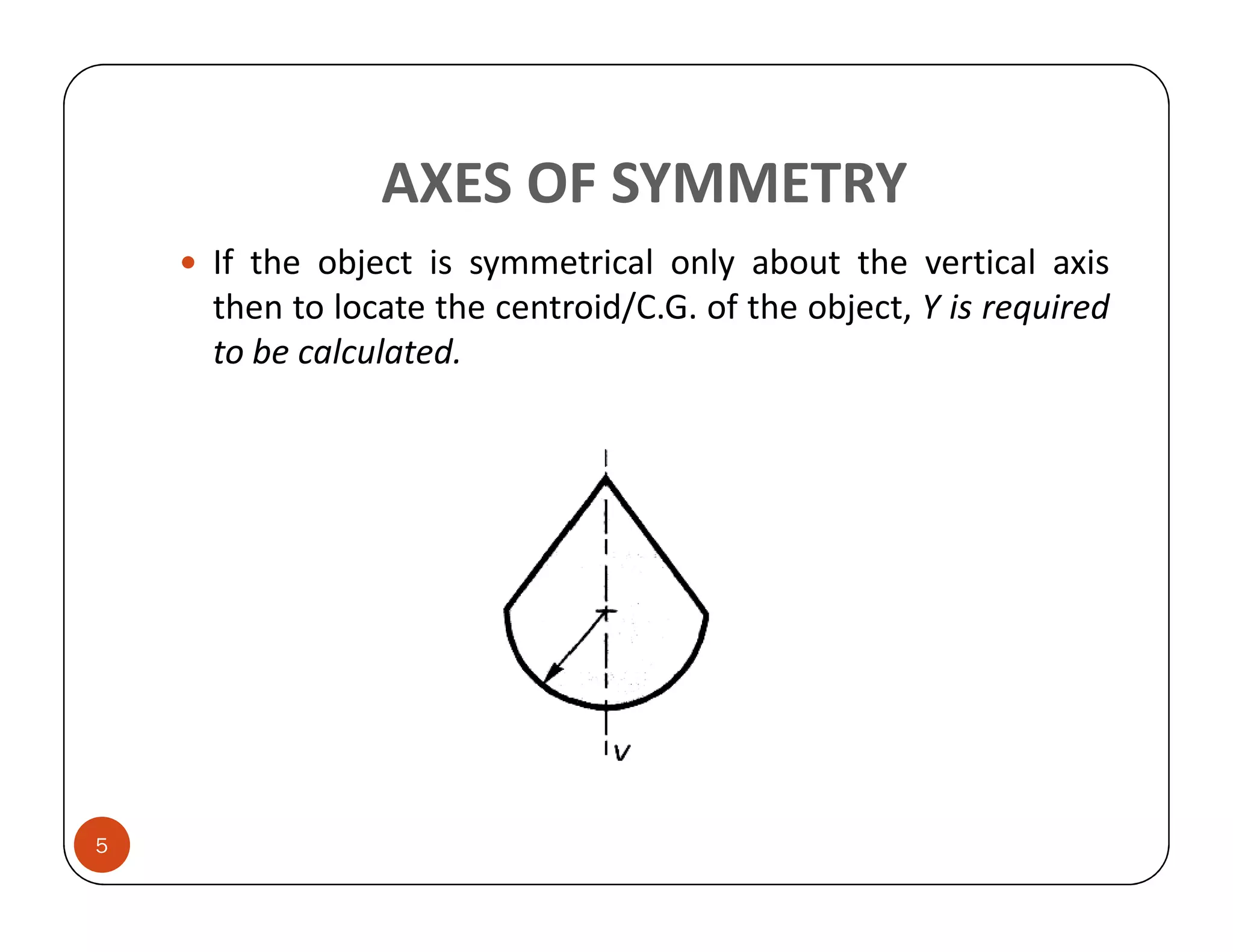
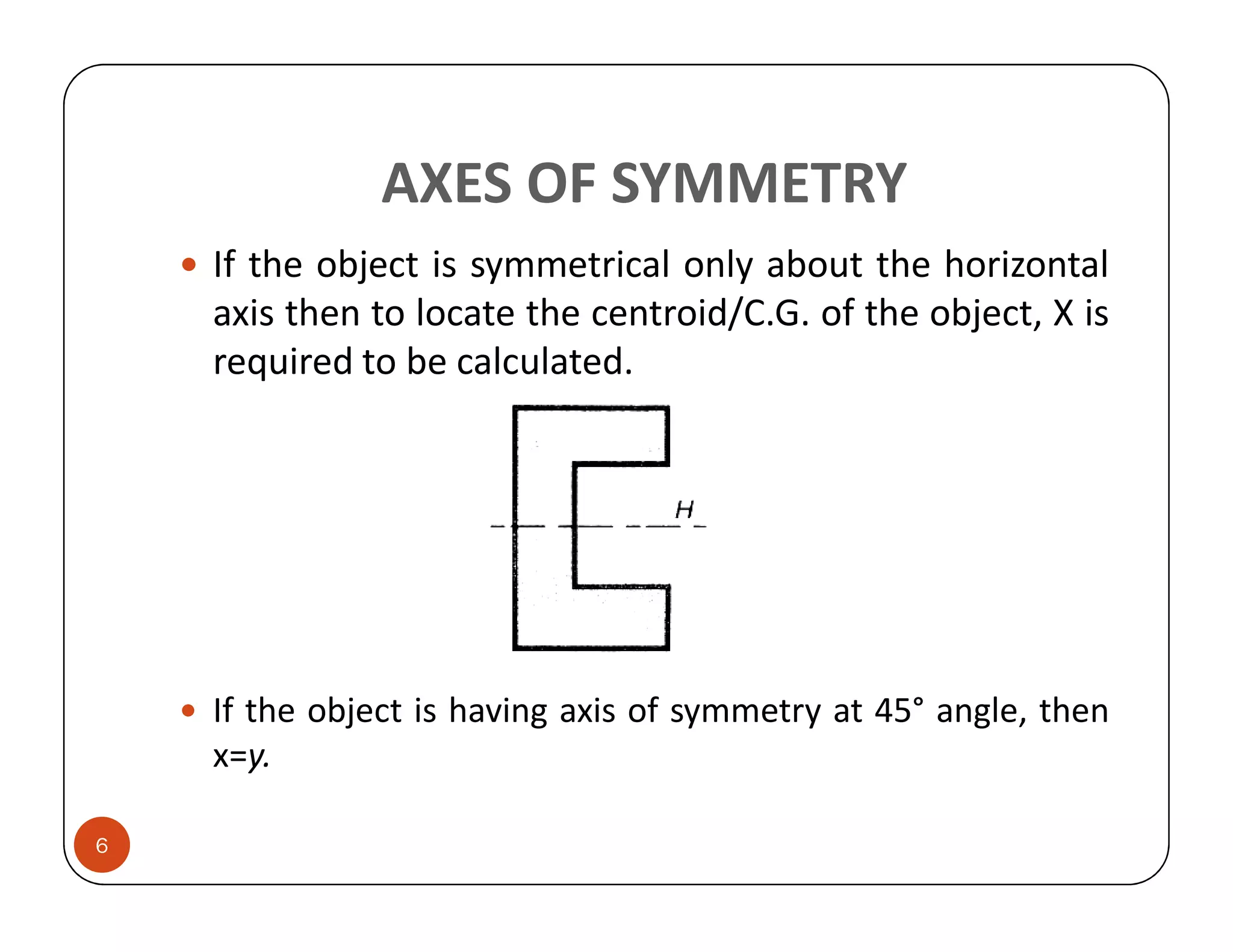
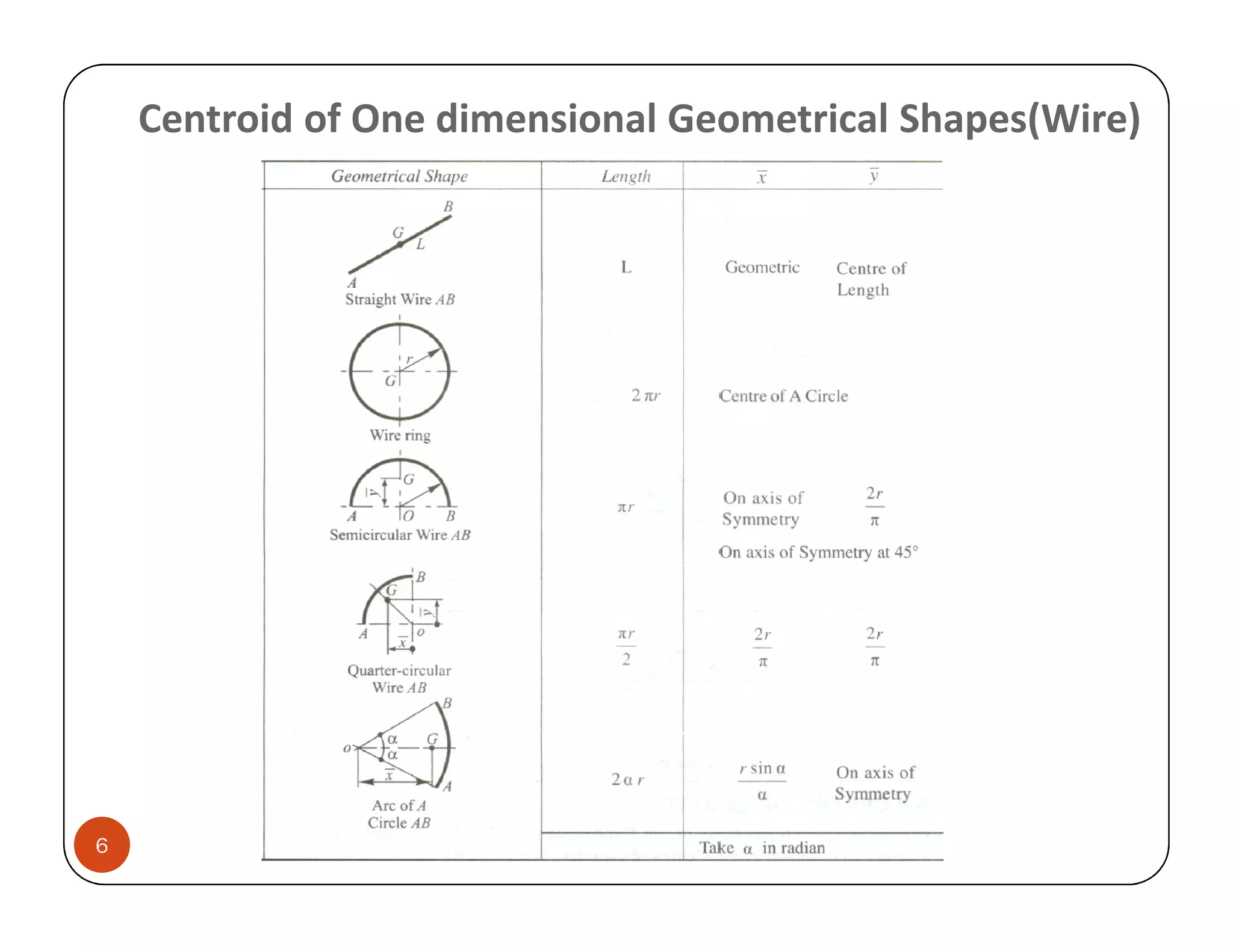
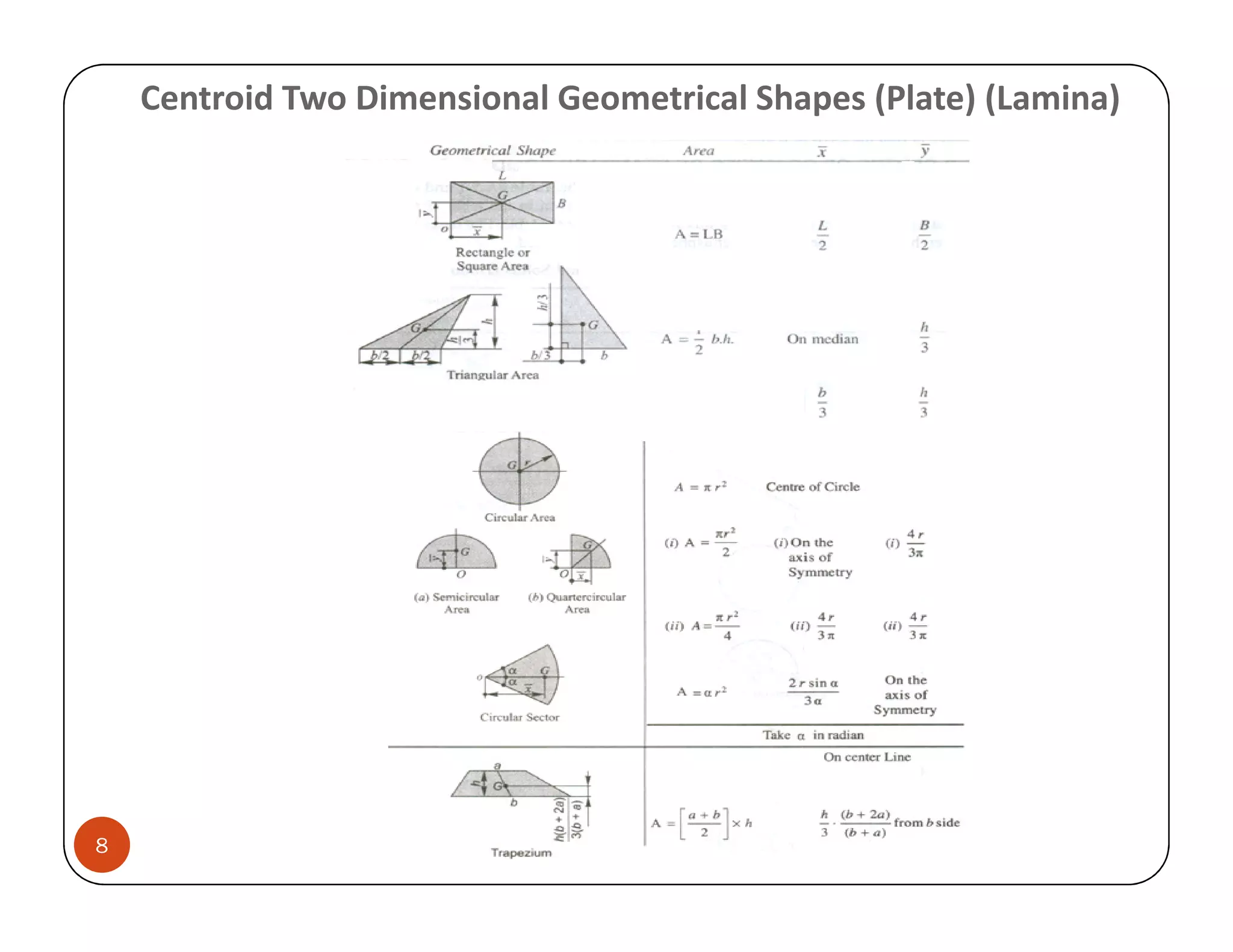
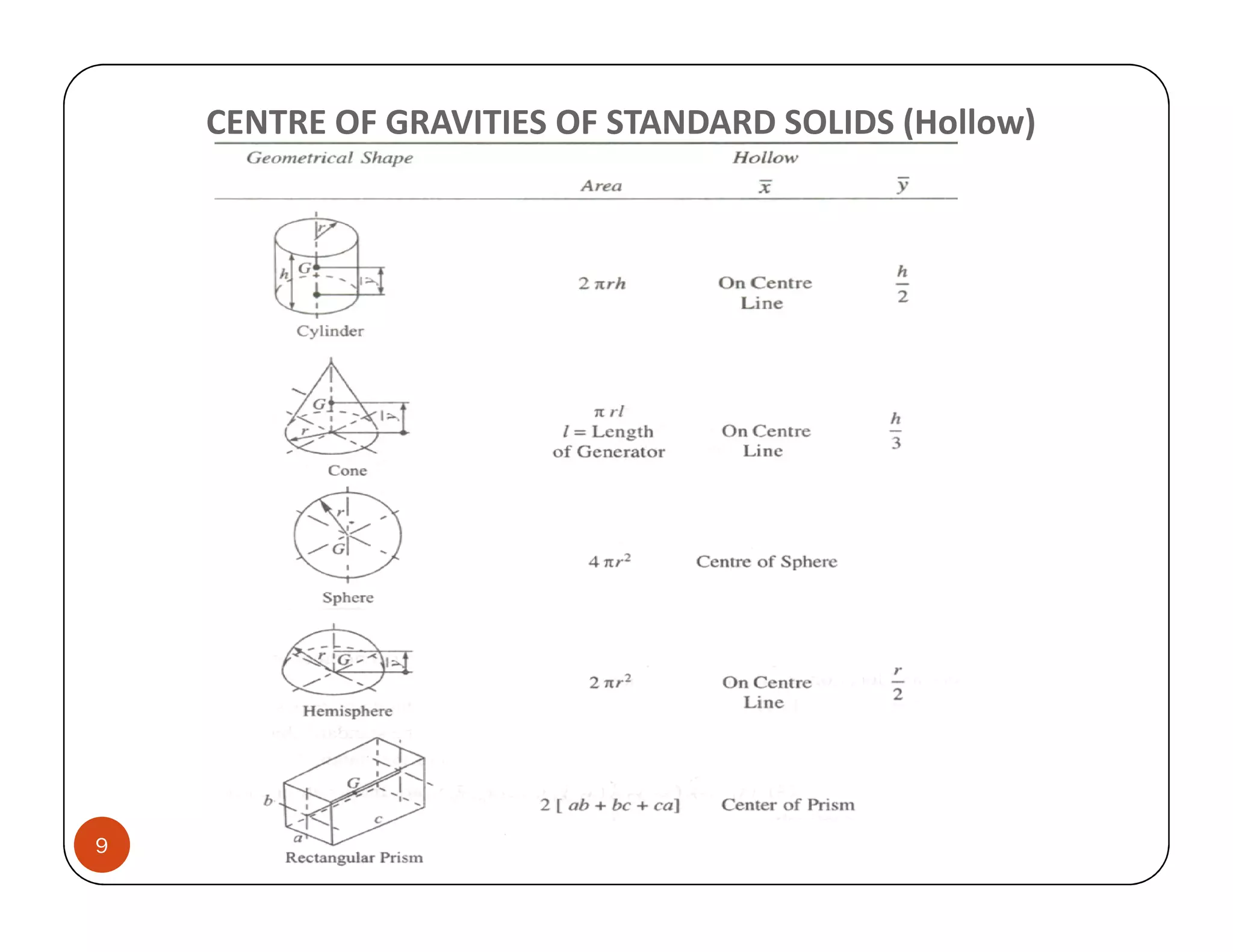
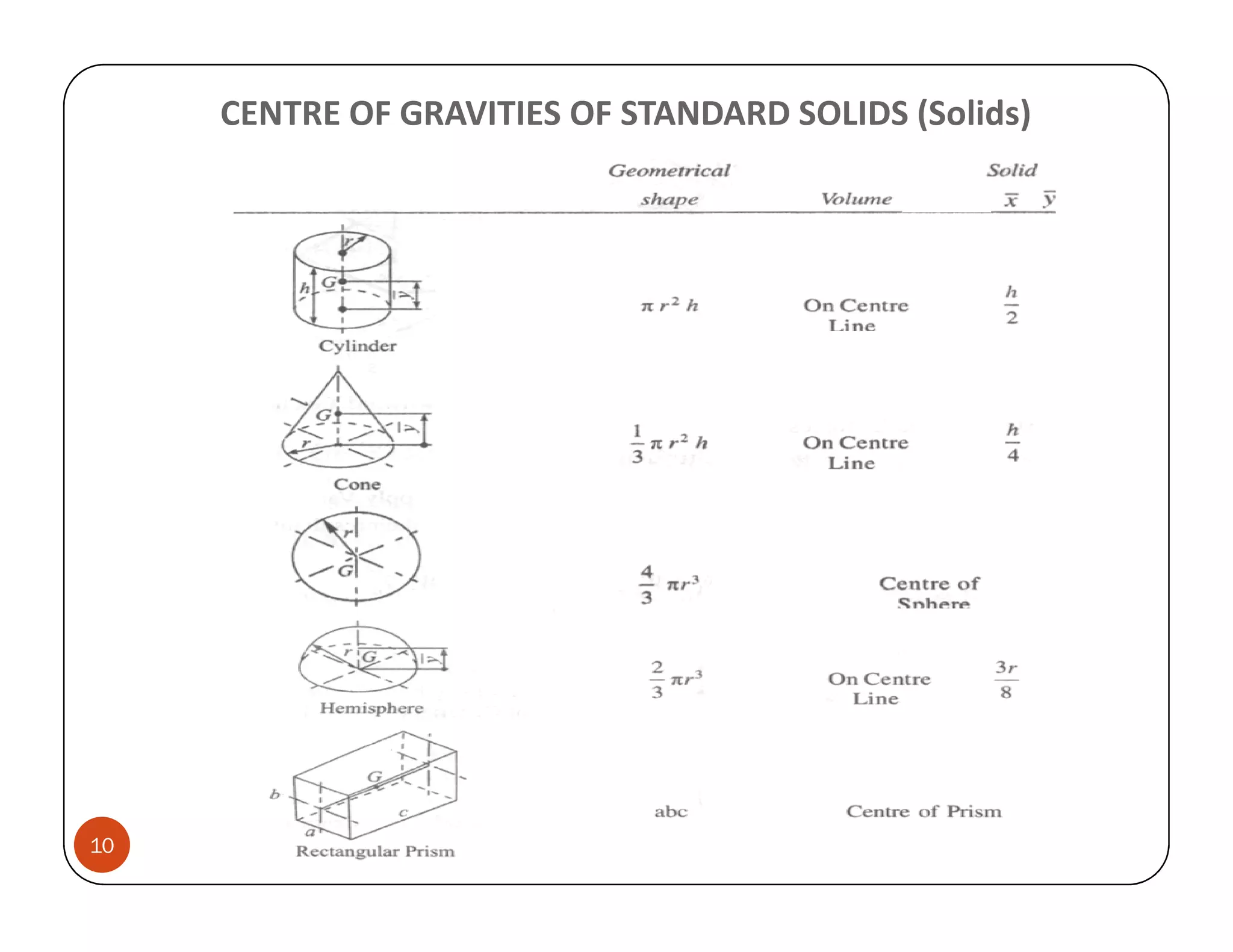
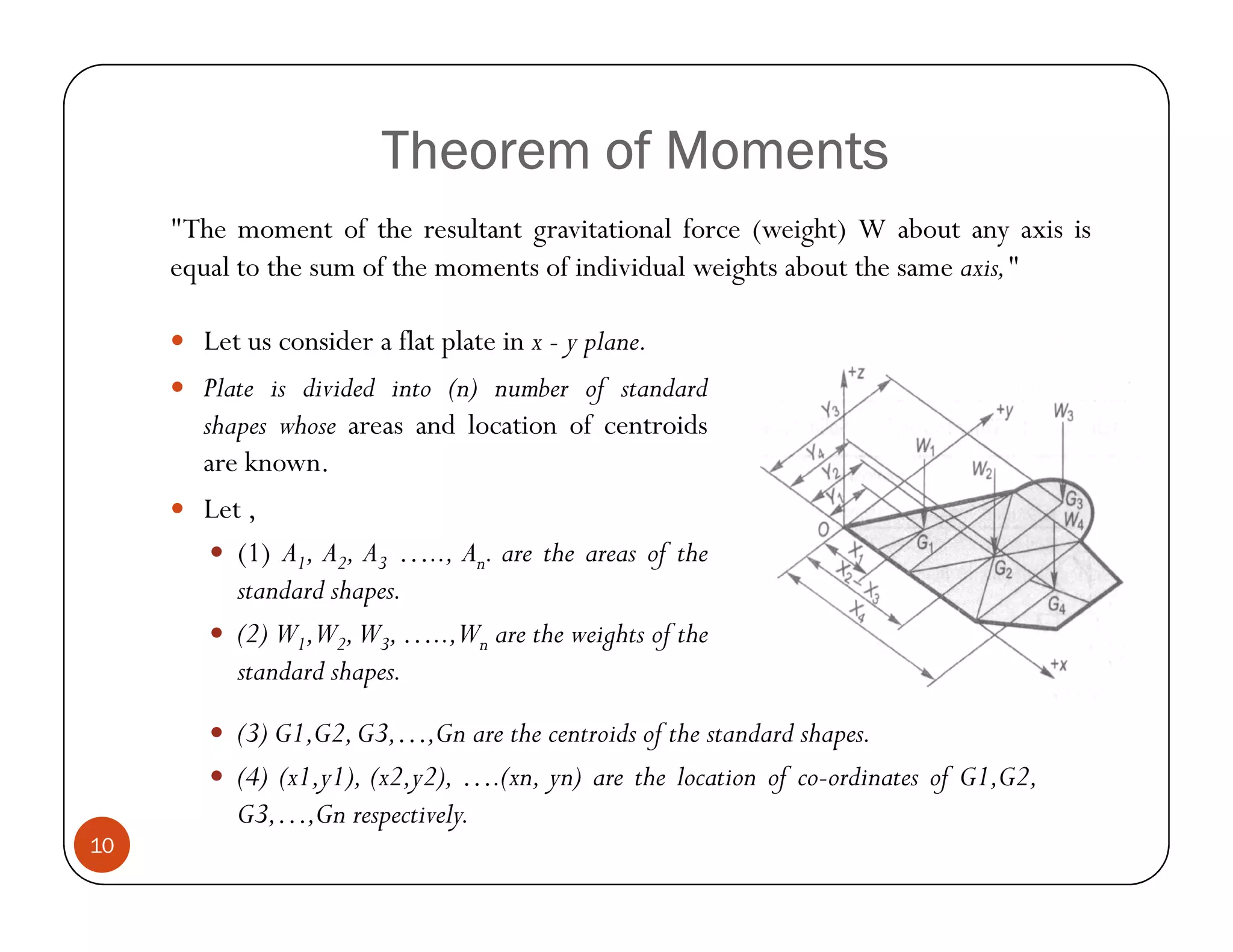
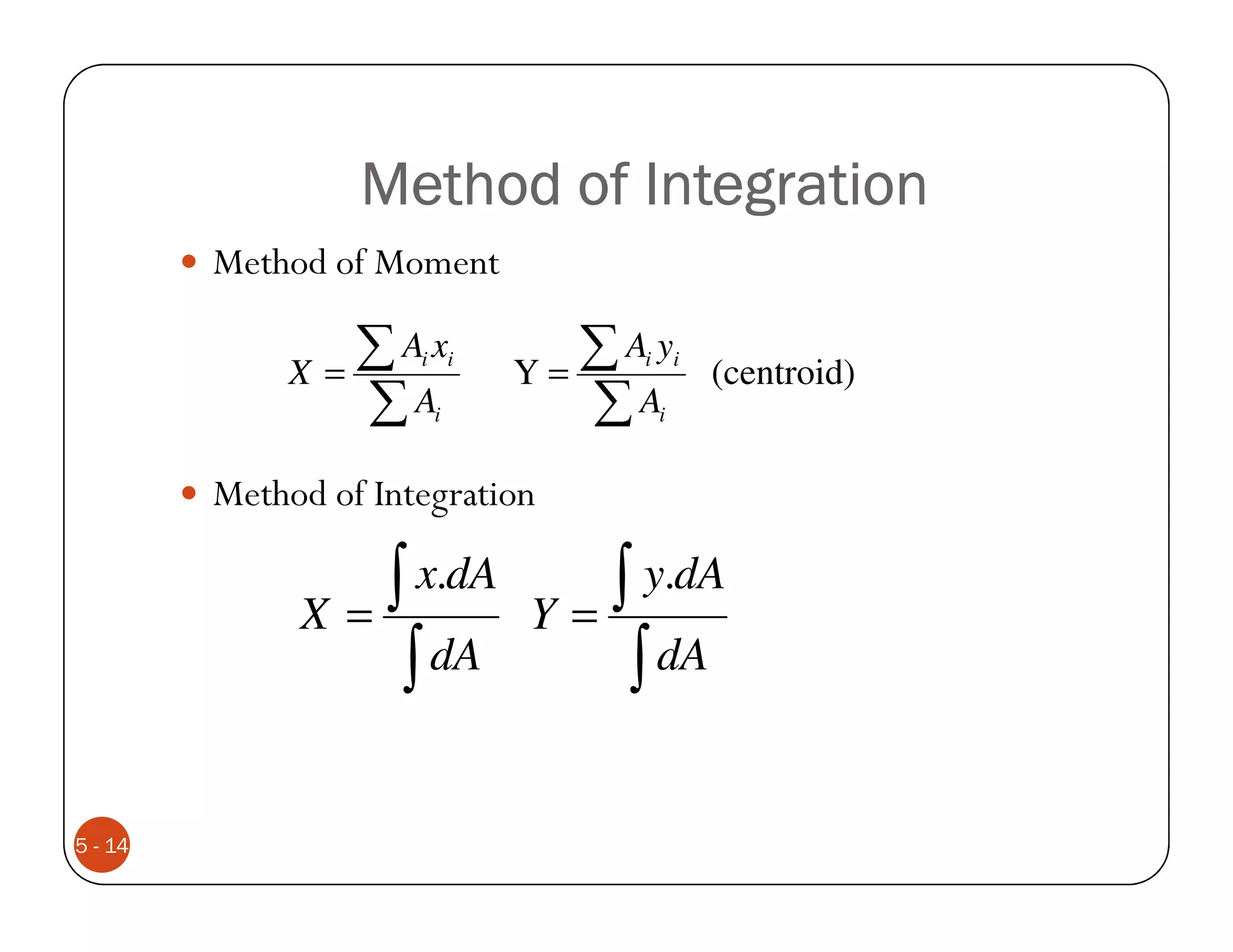
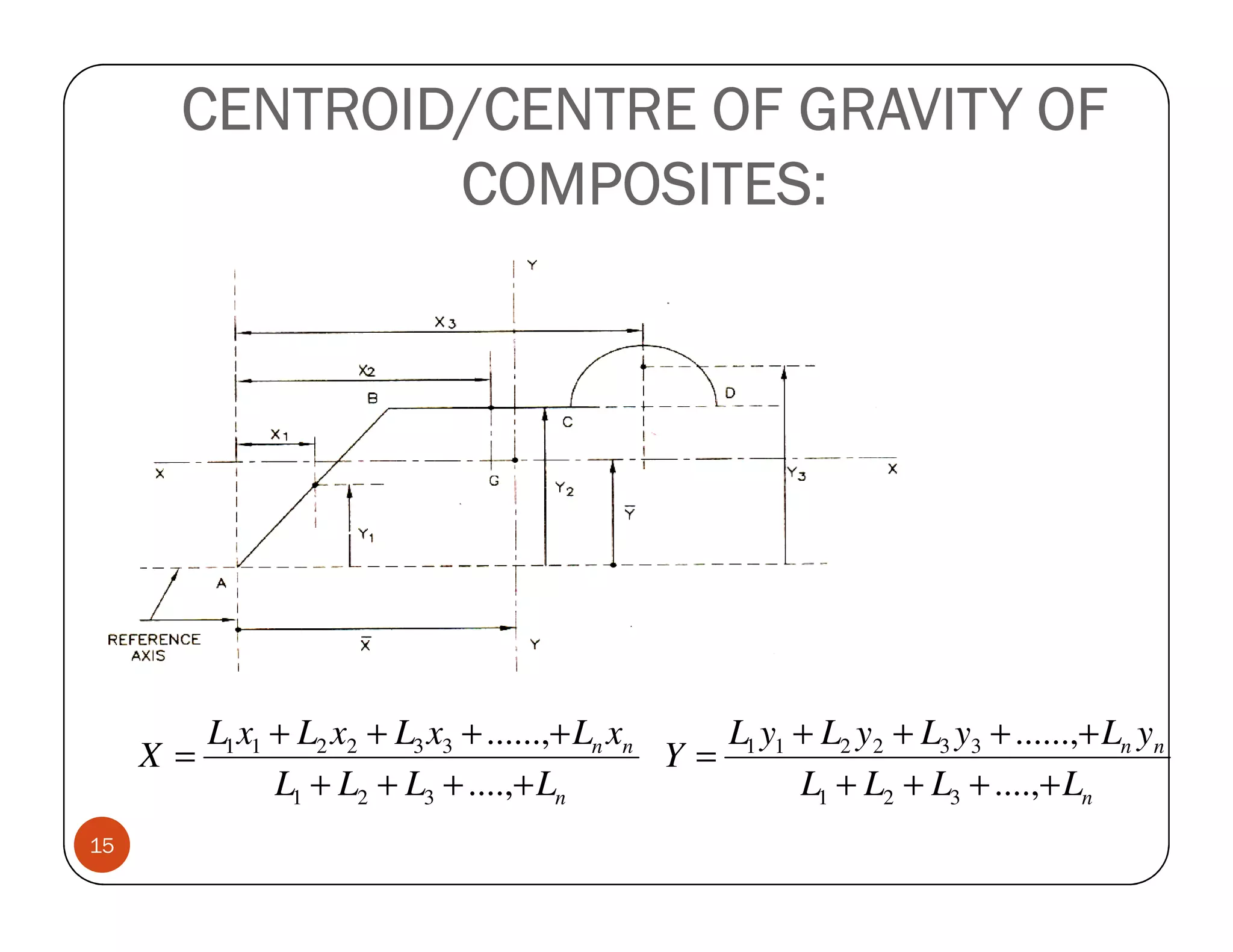
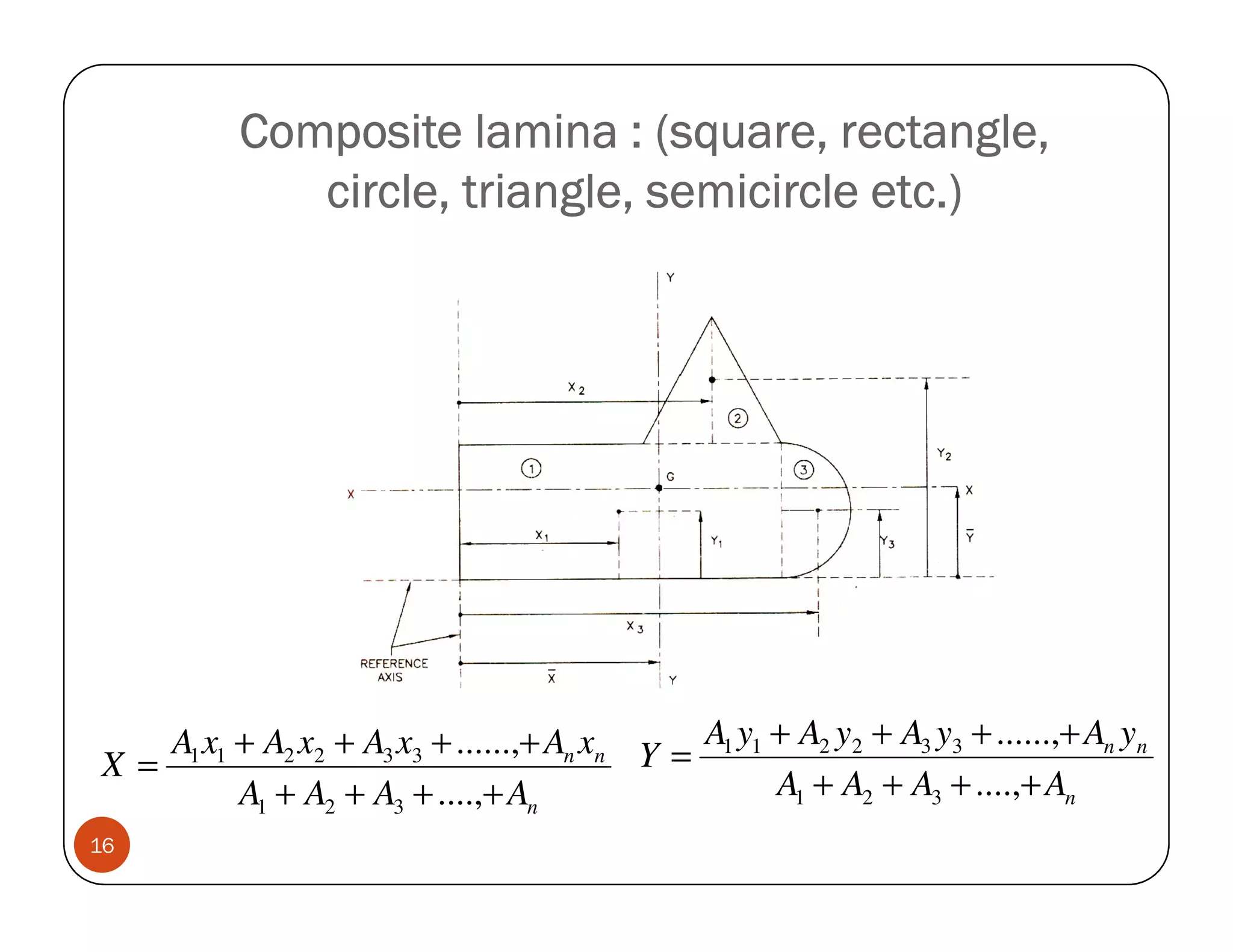
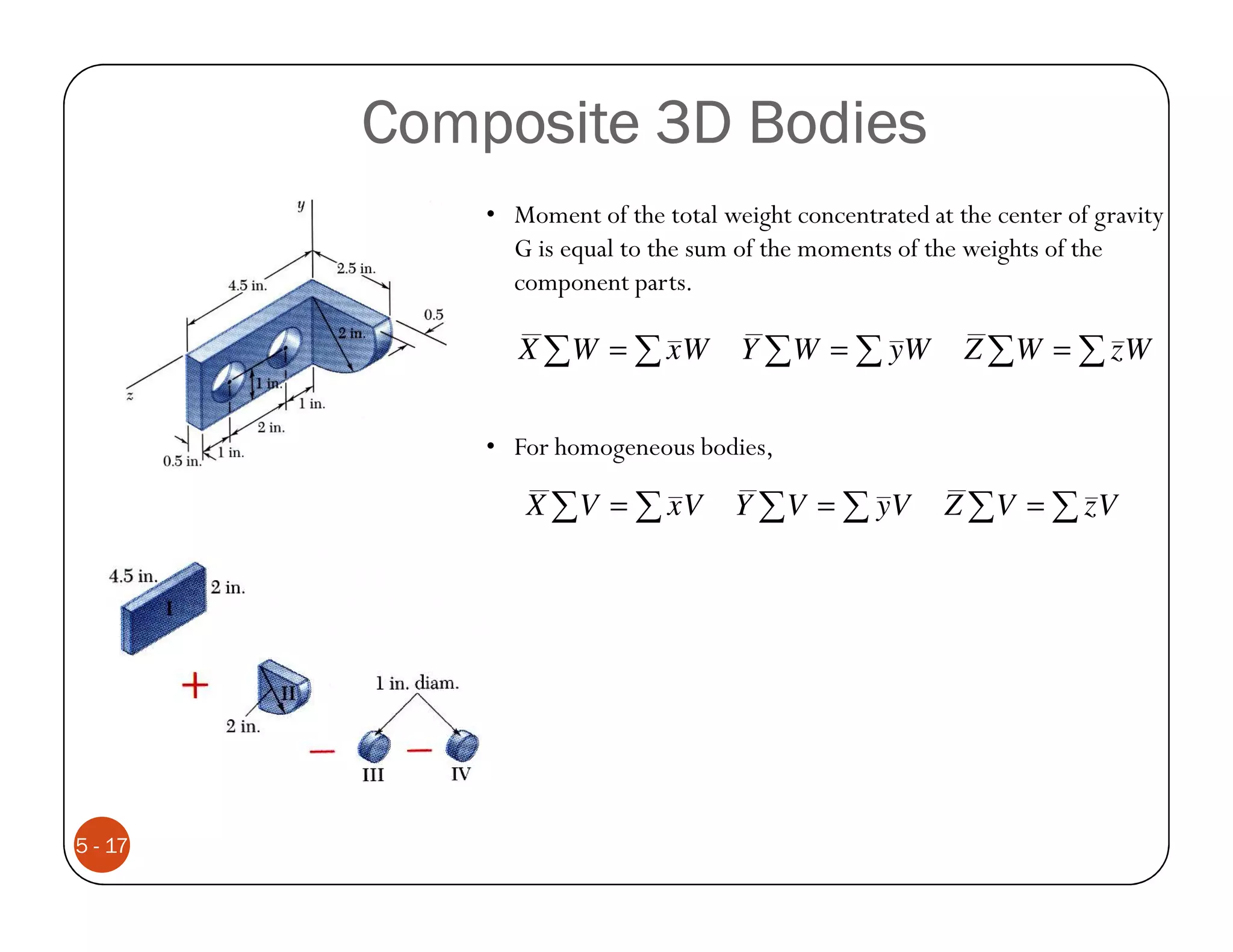
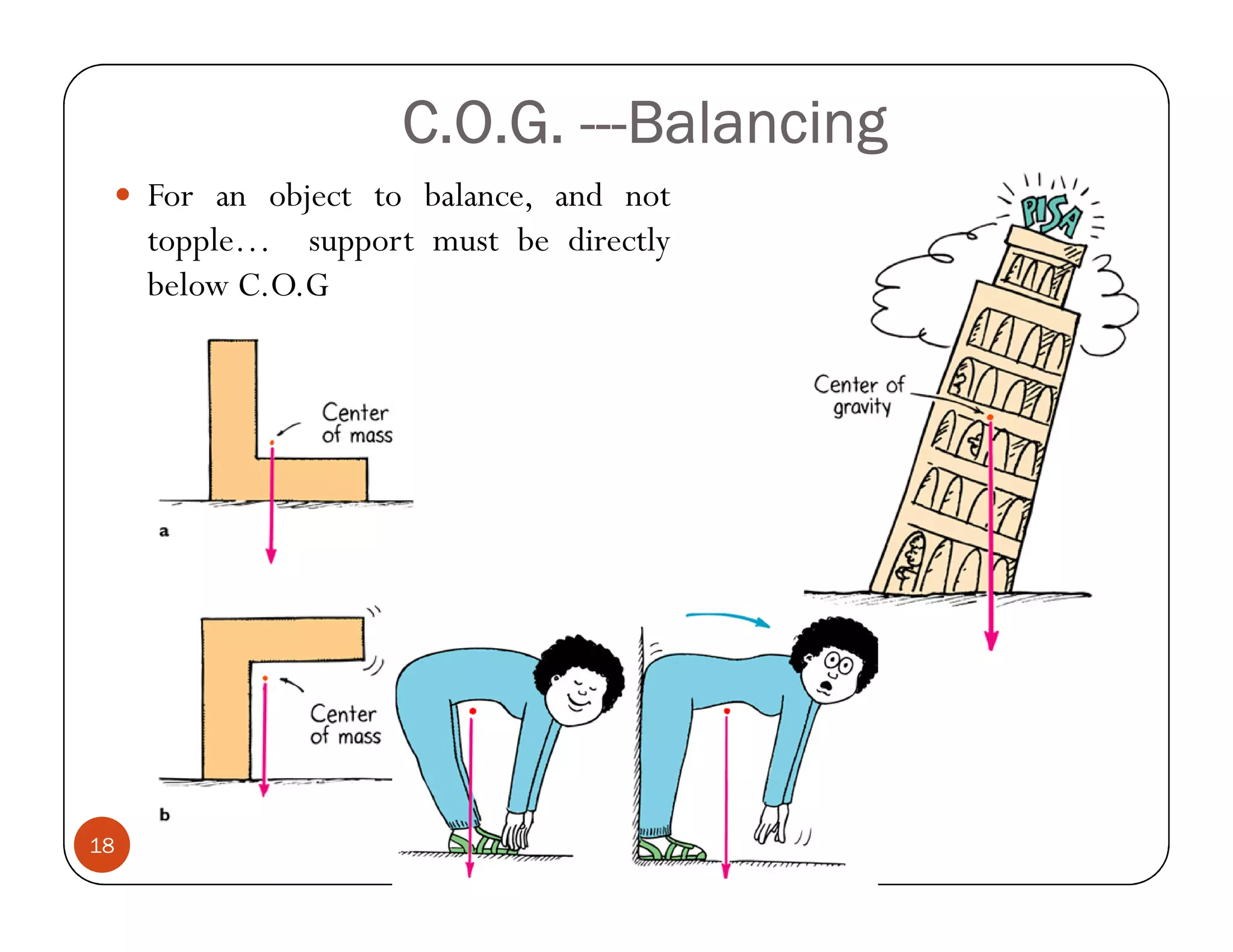
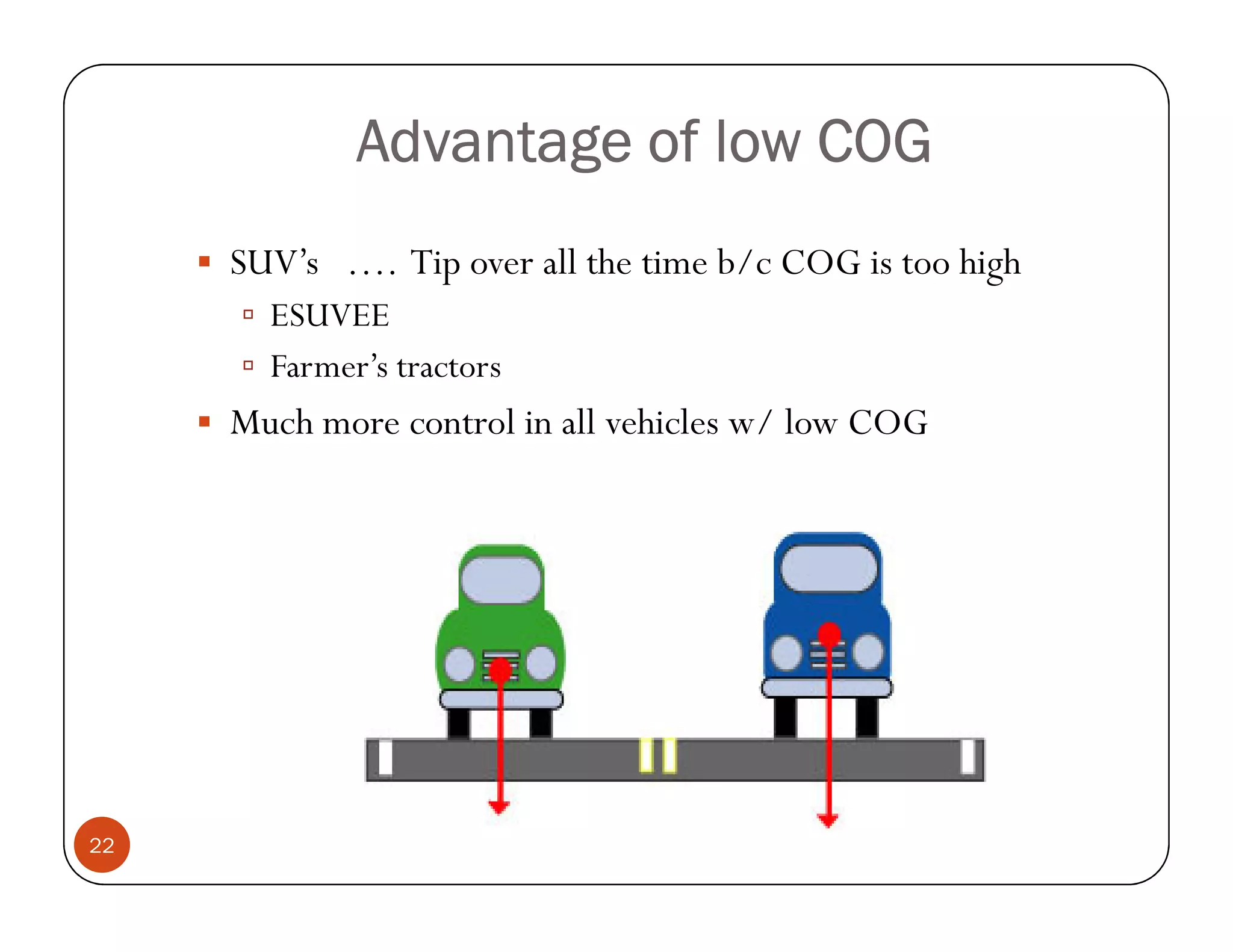
The document discusses the concepts of centroid and centre of gravity. The centroid, also known as the center of gravity, is the point location of an object's average position of weight. For symmetrical objects, the centroid will be at the exact center, but for irregularly shaped objects it depends on the weight distribution. Various methods are described for calculating the centroid of standard shapes, composite objects, and through integration. The centroid is important for balancing objects and determining their stability.

1. Jaydeep Patel
School of Technology,
1

2. Centroid and Centre of Gravity
Centre of gravity of one dimensional body (e.g. wire) and two
dimensional body (e.g. plate) is known as Centroid.
Definition--The Point located at an object’s average position of
the weight.
In other words…. The center of an object’s weight
Symmetrical object’s, like a baseball the C.G. would be in the
exact center of object
However other oddly shaped objects will find COG in any
number of positions, depending on weight distribution
COG
2

3. AXES OF SYMMETRY
First check whether the given composite shape is
symmetrical about any axis or not.
If the object is symmetrical about two axes then the point
of intersection of these two axes locate the Centroid/C.G.
of the object.
3

4. AXES OF SYMMETRY
If the object is symmetrical only about the vertical axis
then to locate the centroid/C.G. of the object, Y is required
to be calculated.
5

5. AXES OF SYMMETRY
If the object is symmetrical only about the horizontal
axis then to locate the centroid/C.G. of the object, X is
required to be calculated.
If the object is having axis of symmetry at 45° angle, then
x=y.
6

6. Centroid of One dimensional Geometrical Shapes(Wire)
6

7. Centroid Two Dimensional Geometrical Shapes (Plate) (Lamina)
8

8. CENTRE OF GRAVITIES OF STANDARD SOLIDS (Hollow)
9

9. CENTRE OF GRAVITIES OF STANDARD SOLIDS (Solids)
10

10. Theorem of Moments
"The moment of the resultant gravitational force (weight) W about any axis is
equal to the sum of the moments of individual weights about the same axis,"
Let us consider a flat plate in x - y plane.
Plate is divided into (n) number of standard
shapes whose areas and location of centroids
are known.
Let ,
(1) A1, A2, A3 ….., An. are the areas of the
standard shapes.
(2) W1,W2, W3, …..,Wn are the weights of the
standard shapes.
(3) G1,G2, G3,…,Gn are the centroids of the standard shapes.
(4) (x1,y1), (x2,y2), ….(xn, yn) are the location of co-ordinates of G1,G2,
G3,…,Gn respectively.
10

11. All weights W1,W2, W3, …..,Wn are acting vertically downward. i.e., this is a system
equivalent to a system of parallel forces.
Resultant W =W1 +W2 +W3, …..,+Wn ( )
To get the position co-ordinates (x, y) of the resultant, apply Varignon's Principle and
equate moments of W1,W2, W3, …..,Wn about x-axis with the moment of their resultant
W about the same x-axis
W Y =W1Y1+W2Y2 +W3Y3 + .....+WnYn
Similarly equating the moments about y-axis, we get
W X =W1 X1 +W2 X2 +W3 X3 + .....+Wn Xn
If the complete plate is of the same material and if the thickness of the plate is
same through out, the areas A1, A2, A3 …, An can be written in place of W1,W2, W3,
…..,Wn . Hence
A1 y1 + A2 y2 + A3 y3 + ...... + An yn A1 x1 + A2 x2 + A3 x3 + ...... + An xn
Y= X=
A1 + A2 + A3 + .... + An A1 + A2 + A3 + .... + An
11 If any area is negative then (-ve) sign is used before that area.

12. 1. Similarly for one dimensional objects (e.g wire)
L1 x1 + L2 x2 + L3 x3 + ......,+ Ln xn
X=
L1 + L2 + L3 + ....,+ Ln
L1 y1 + L2 y2 + L3 y3 + ......,+ Ln yn
Y=
L1 + L2 + L3 + ....,+ Ln
2. Similarly for Solid objects (e.g having 3-dimensional)
V1 x1 + V2 x2 + V3 x3 + ......,+Vn xn
X=
V1 + V2 + V3 + ....,+Vn
V1 y1 + V2 y2 + V3 y3 + ......,+Vn yn
Y=
V1 + V2 + V3 + ....,+Vn
12

13. 3. For object made of different density materials
W1 x1 + W2 x2 + W3 x3 + ......,+Wn xn
X=
W1 + W2 + W3 + ....,+Wn
W1 y1 + W2 y2 + W3 y3 + ......,+Wn yn
Y=
W1 + W2 + W3 + ....,+Wn
CENTROID & CENTRE OF GRAVITY
X =
∑ dLx Y=
∑ dLy (centroid)
∑ dL ∑ dL
X=
∑Ax i i
Y=
∑Ay i i
(centroid)
∑A i ∑A i
X =
∑Vρx Y=
∑Vρy (centre of Gravity)
13 ∑Vρ ∑ Vρ

14. Method of Integration
Method of Moment
X=
∑Ax i i
Y=
∑Ayi i
(centroid)
∑A i ∑A i
Method of Integration
X=
∫ x.dA Y=
∫ y.dA
∫ dA ∫ dA
5 - 14

15. CENTROID/CENTRE OF GRAVITY OF
COMPOSITES:
L1 x1 + L2 x2 + L3 x3 + ......,+ Ln xn L1 y1 + L2 y2 + L3 y3 + ......,+ Ln yn
X= Y=
L1 + L2 + L3 + ....,+ Ln L1 + L2 + L3 + ....,+ Ln
15

16. Composite lamina : (square, rectangle,
circle, triangle, semicircle etc.)
A1 x1 + A2 x2 + A3 x3 + ......,+ An xn Y = A1 y1 + A2 y2 + A3 y3 + ......,+ An yn
X=
A1 + A2 + A3 + ....,+ An A1 + A2 + A3 + ....,+ An
16

17. Composite 3D Bodies
• Moment of the total weight concentrated at the center of gravity
G is equal to the sum of the moments of the weights of the
component parts.
X ∑W = ∑ xW Y ∑ W = ∑ yW Z ∑W = ∑ zW
• For homogeneous bodies,
X ∑V = ∑ xV Y ∑ V = ∑ yV Z ∑V = ∑ zV
5 - 17

18. C.O.G. ---Balancing
---Balancing
For an object to balance, and not
topple… support must be directly
below C.O.G
18

19. Balancing Stuff
Again, all that has to happen to balance, is for a support to be
directly beneath COG
19

20. Where C.O.G. is located
Generally found in the middle of
all the weight…
Does not even have to be within,
the object itself
Ex. boomerang
Will be located toward one side of
an object where most of its mass is
focused…
Ex. Weebles
C.G
20

21. Weebles Wobble, but they don’t fall
down???
Weebles have very low COG
Whenever rolling it will roll to a stop
when its COG is as low as possible
This occurs when it is standing upright
Also occurs for inflatable toy clowns
Objects with a low COG are less likely
to topple because of this principle
Higher COG is, the easier to topple
21

22. Advantage of low COG
SUV’s …. Tip over all the time b/c COG is too high
ESUVEE
Farmer’s tractors
Much more control in all vehicles w/ low COG
22

23. Centroid of Standard Shapes by
Integration
Centroid of a Triangle
ABC is having a base BC=b and altitude
h as shown.
Let us take elementary strip PQ at a
height (x) from the base and of
thickness (dx) as shown.
now, ∆ APQ and ∆ ABC are similar,
since PQ is taken parallel to BC.
23

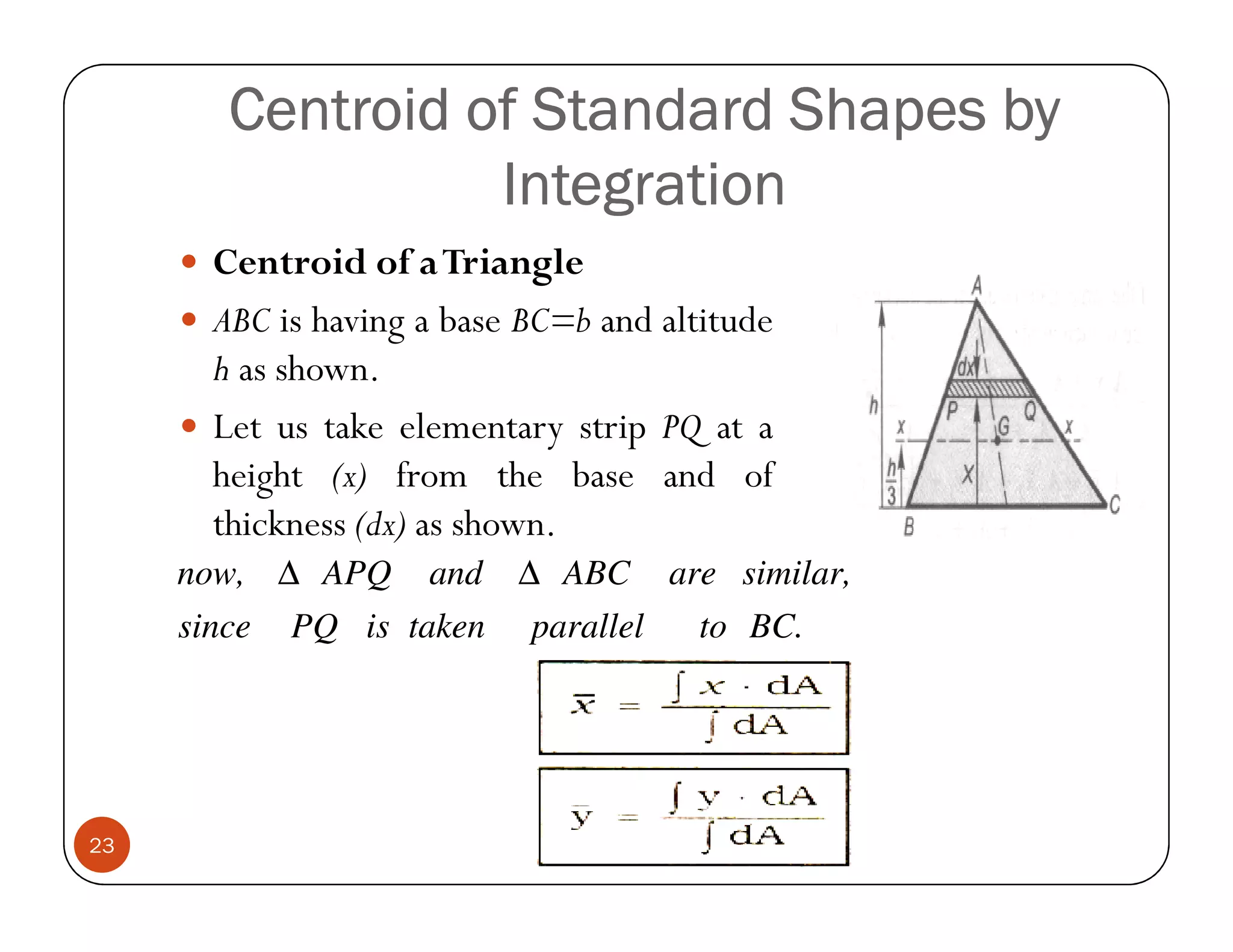
24. PQ h − x (h - x)
∴ = ∴ PQ = b
BC h h
(h - x)
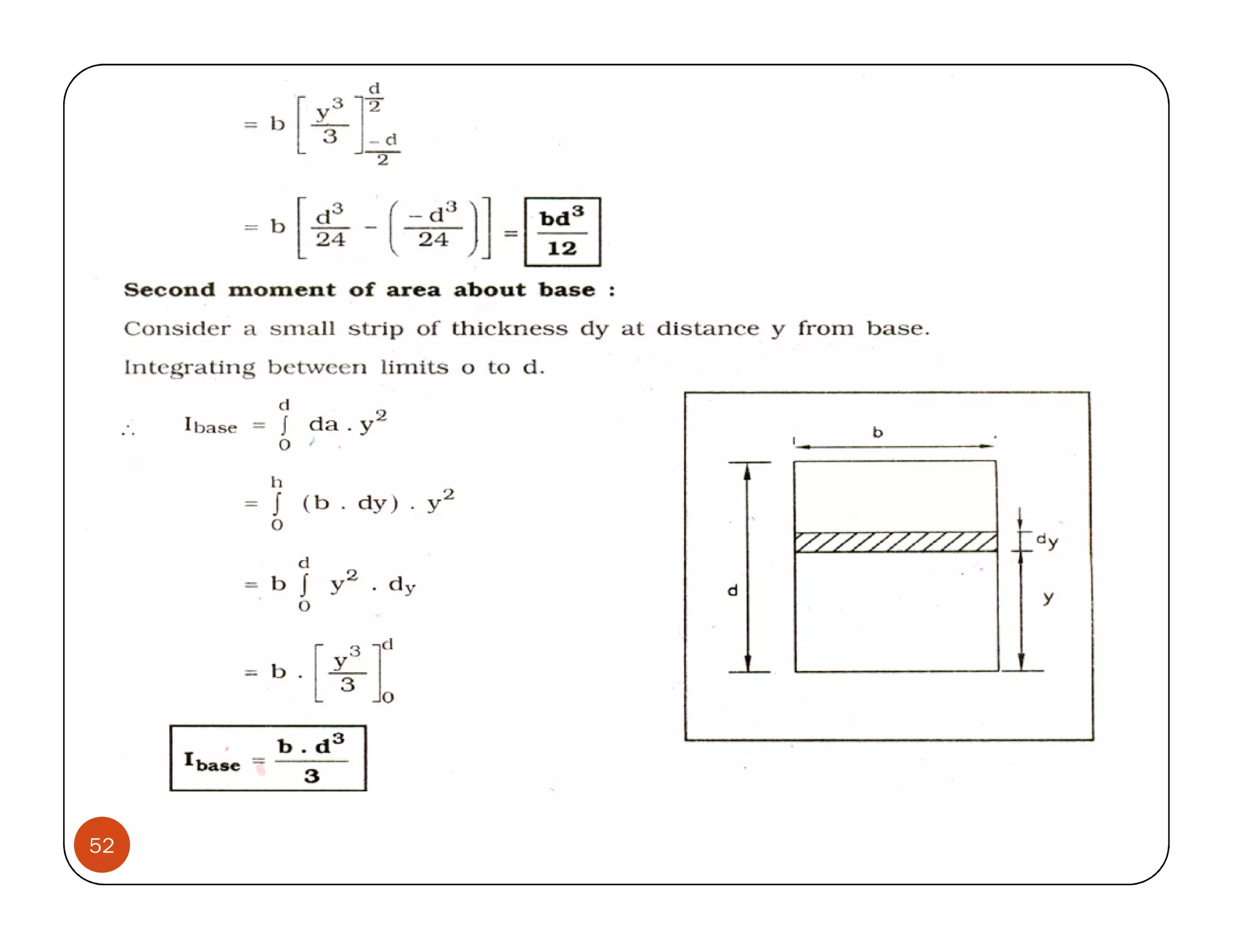
Now area of the elementry stripe PQ = (PQ)(dx) = b. dx
h
(h − x)
now [moment of the elementry strip about base BC] = [ b. dx]. [x ]
h
now equating moments of the area of the triangle about BC, we have
h h
(h − x)b (h − x)b
∫ h
0
. x. dx = y ( A) = y ∫
0
h
. dx
h h
 b   b 
∫ h 
0
bx − x 2 . dx = y ∫  b − x . dx
0
h 
h h
 bx 2 b x 3   b x2 
 − .  = y bx − . 
 2 h 3 0  h 2 0
h
y=
24 3

25. Centroid of A Semicircle
25

26. 26

27. Theorems of Pappus-Guldinus
Pappus-
• Surface of revolution is generated by rotating a plane curve
about a fixed axis.
• Theorem 1:
• Area of a surface of revolution is equal to the
length of the generating curve times the
distance traveled by the centroid through the
rotation.
A = 2π yL
27

28. Theorems of Pappus-Guldinus
Pappus-
• Body of revolution is generated by rotating a plane area about a
fixed axis.
• Theorem 2:
• Volume of a body of revolution is equal to the
generating area times the distance traveled by
the centroid through the rotation.
V = 2π y A
28

29. Sample Problem
SOLUTION:
• Apply the theorem of Pappus-Guldinus to
evaluate the volumes or revolution for the
rectangular rim section and the inner cutout
section.
• Multiply by density and acceleration to get the
mass and acceleration.
The outside diameter of a pulley is 0.8 m, and
the cross section of its rim is as shown.
Knowing that the pulley is made of steel and that
the density of steel is
determine the mass and weight of the rim.
ρ = 7.85 ×103 kg m 3
29

30. Sample Problem
SOLUTION:
• Apply the theorem of Pappus-Guldinus to evaluate
the volumes or revolution for the rectangular rim
section and the inner cutout section.
• Multiply by density and acceleration to get the mass
and acceleration.
( 3 3
)( 6  −9 3
3 3
) m = 60.0 kg
m = ρV = 7.85 × 10 kg m 7.65 × 10 mm 10 m mm 
 
30 (
W = mg = (60.0 kg ) 9.81 m s 2 ) W = 589 N

31. Stable, Unstable and Neutral
Equilibrium
Stable Equilibrium
A body is said to be in the Stable Equilibrium if it returns back to
its original position of equilibrium after it is slightly disturbed
from its position of equilibrium. In fact forces, acting on the body
after it disturbed, will have tendency to bring the body back to its
original position of equilibrium.
In case of stable bodies C.G. is raised when it is disturbed.
31

32. Neutral Equilibrium
A body is said to be in Neutral Equilibrium if it remains in
equilibrium in the newly disturbed position.
In fact forces, acting on the body after it is disturbed, are also in
equilibrium.
In case of neutral bodies C.G. is neither raised nor lowered when it is
disturbed i.e., Level of C.G remains unaltered.
32

33. Unstable Equilibrium
A body is said to be in Unstable Equilibrium if it does not return
back to its original position of equilibrium after it is slightly
disturbed.
In fact forces, acting on the body after it is disturbed, will Have a
tendency to move the body further away from its original position
of equilibrium.
In case of unstable bodies C.G. is lowered when it is disturbed.
33

34. 34

35. Moment of Inertia
Characteristics of the material, suitable cross-section of the
component and it's proper orientation w.r.t. the forces, torques,
couples, moments etc. acting on it are very important in the design of
the component for it's lifelong trouble less function.
Once the material is selected, the cross section of the component and
its orientation with respect to the load system are of utmost
importance.
35

36. Case (i). In first case the beam bends a lot.
In this case we have kept smaller dimension of the two of the cross-
section in the plane of bending. Material offers less resistance against
bending.
Case (ii). In second case the beam bends a little.
In this case we have kept larger dimension of the two, of the cross-
section, in the plane of bending.
36

37. Material offers sufficient resistance against bending.
From Case (i) and (ii) we can observe that orientation of the cross-section
w.r.t. load system plays a vital role in developing resistance against
deformation.
The load carrying capacity of any member depends upon the material and
the M.I. of cross-section. Ultimately it leads to Modulus of Section.
37

38. What is Moment of Inertia?
Defn:
The second moment of area, also known as the area moment of
inertia, moment of inertia of plane area, or second moment of
inertia is a property of a cross section that can be used to predict the
resistance of beams to bending and deflection, around an axis that lies in
the cross-sectional plane.
The deflection of a beam under load depends not only on the load,
but also on the geometry of the beam's cross-section.
38

39. Moment of Inertia
39

40. The radius of gyration
The radius of gyration of an area is defined as the imaginary
radius from the reference axis where the whole area is assumed to
be concentrated.
40

41. 41

42. 42

43. Polar Moment of Inertia
Polar moment of inertia is a quantity used to predict an object's ability to
resist torsion, in objects (or segments of objects) with an invariant circular cross
section
Ip = ∫
A
ρ 2 dA
∫ (x )
2
Ip = + y 2 dA
A
Ip = ∫
A
x 2 dA + ∫
A
y 2 dA
I p = I xx + I yy
43

44. Theorem of Perpendicular Axis
"If Ixx and Iyy be the moments of inertia of a plane section about two
perpendicular axes meeting at o, the moment of inertia Izz about the
z-z axis, perpendicular to the plane and passing through the
intersection of x-x and y-y axes is given by:
Izz = Ixx + Iyy ”
44

45. 45

46. Theorem of Parallel Axes
(or)
Theorem of Transfer of Axes
If the M.I. of a plane area A about centroidal x and y axes be denoted
by IxxG and IyyG then the M.I. of the same area A about axes x' and y'
parallel to x and y axes at a distance (d) and (c) respectively is given
by:
Ix'x' = IxxG + Ad2 and Iy'y' = IYYG + Ac2
46

47. This parallel axes theorem is very important since it is of great use in
computing M.I. of the composite areas.
Let us consider an area (A) in the xy plane as shown. Draw x-axis
and y-axis passing through the centroid G of the area (A) under
consideration.
Now draw axis x' parallel to x-axis and at a distance (d) from it.
Similarly draw axis y' parallel to y-axis and at a distance (c) from it.
Take elementary area dA having (x, y) co-ordinates with respect to x
and y axes and having (x', y') co-ordinates with respect to x' and y'
axes.
47

48. 48

49. Second Method
I x′x′ = ∑ dA(d + y ) 2
= ∑ dA(d 2 + 2dy + y 2 )
= ∑ d dA + ∑ 2 yd .dA + ∑ y dA
2 2
= Ixx + Ad 2
Same we can find the Iy'y'
49

50. Section Modulus
50

51. Example-1: Determine the second moment of area of a rectangle about an
through the centroid and parallel to the base.
Also find second moment of area about the base of the rectangle.
Soln:
51

52. 52

53. 53

54. 54

55. 55

56. 56

57. 57