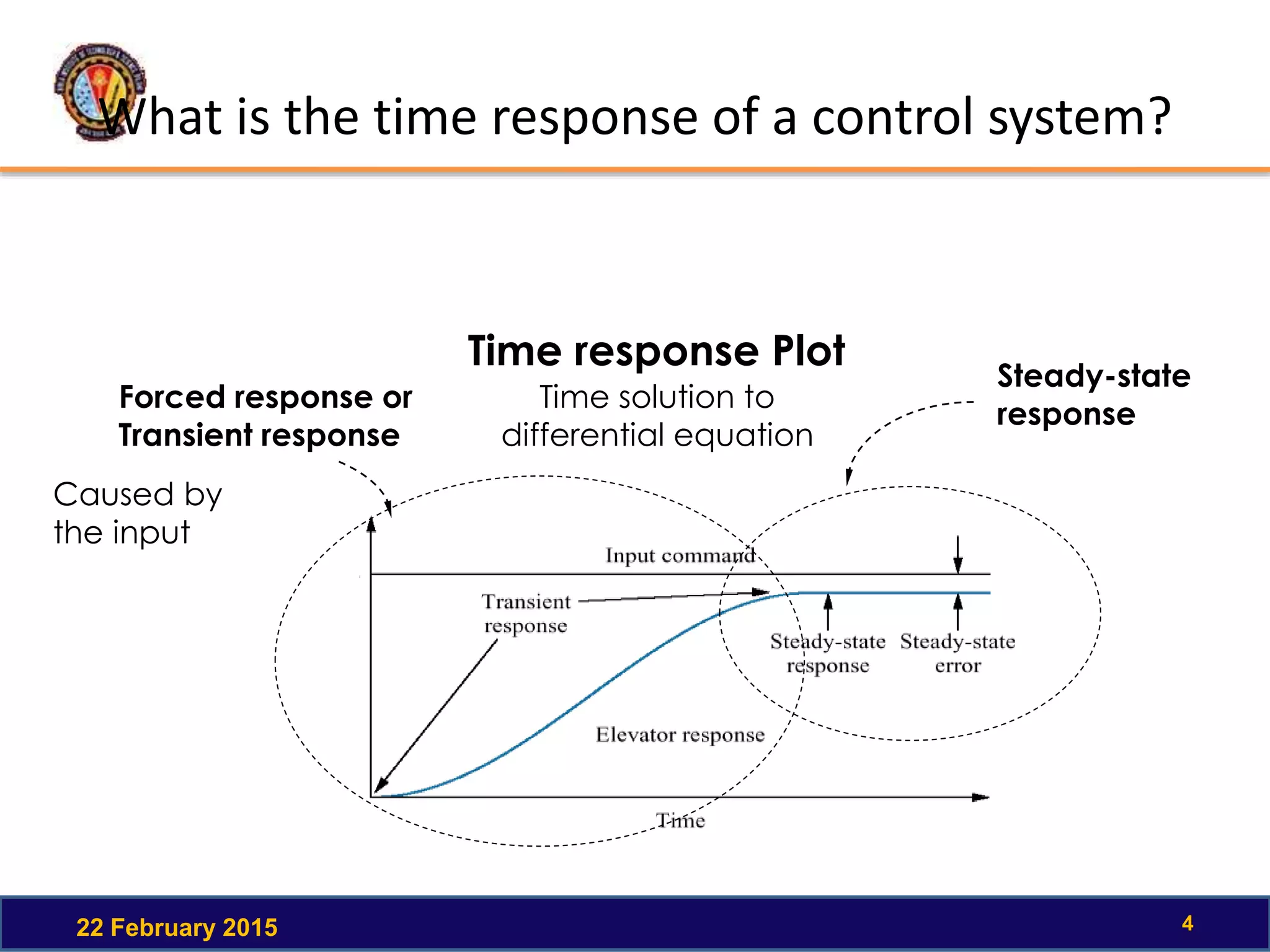
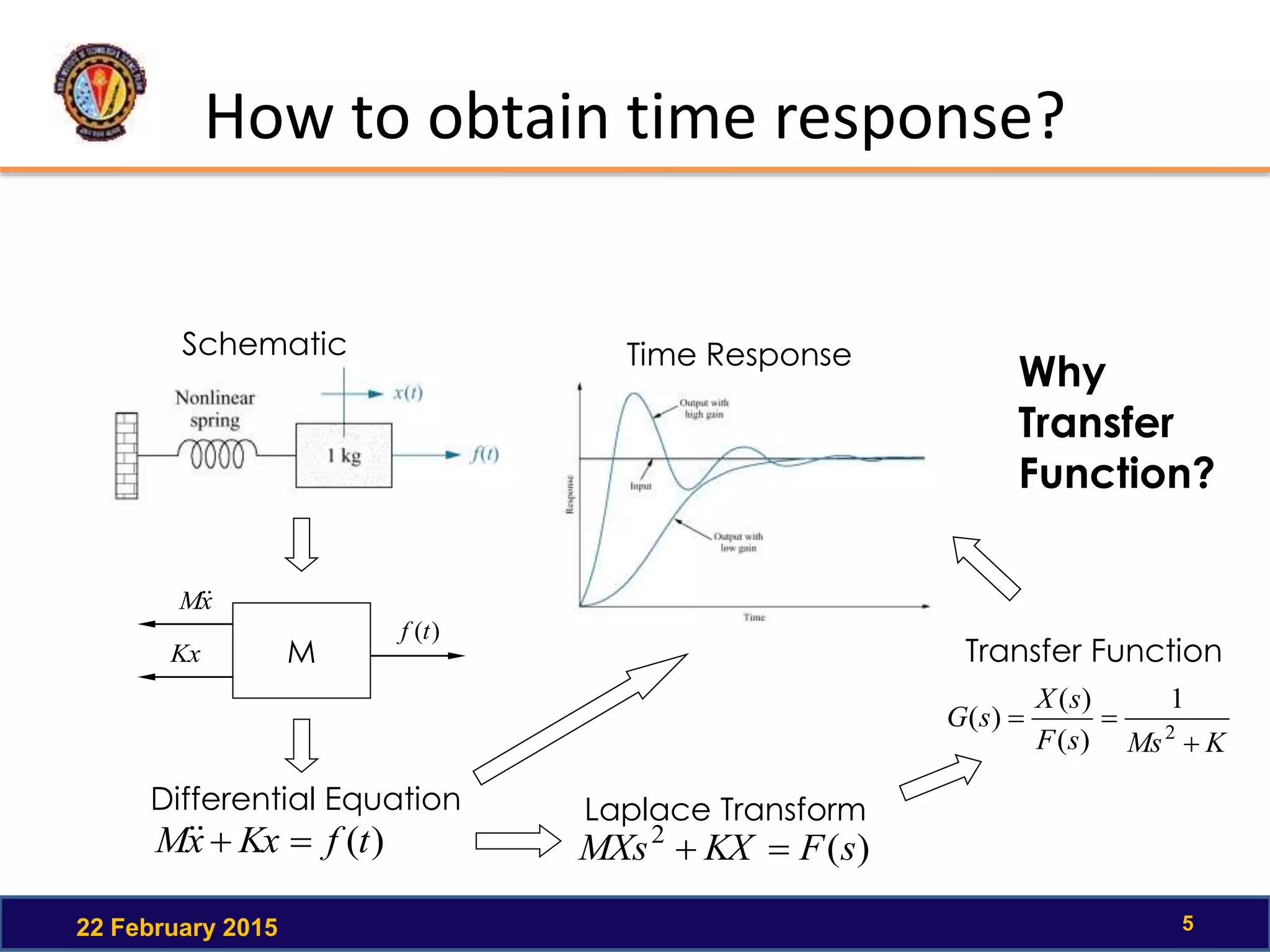
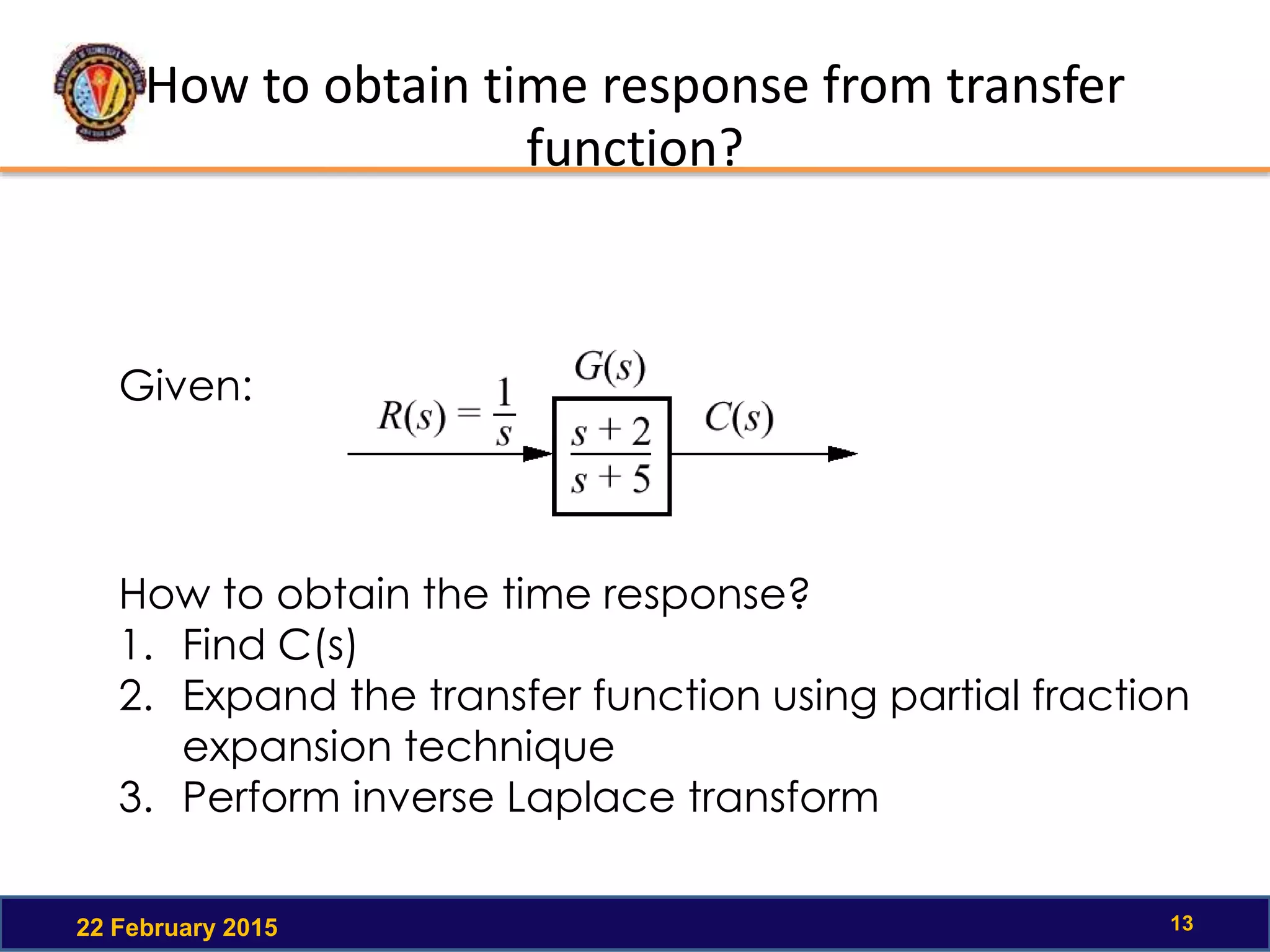
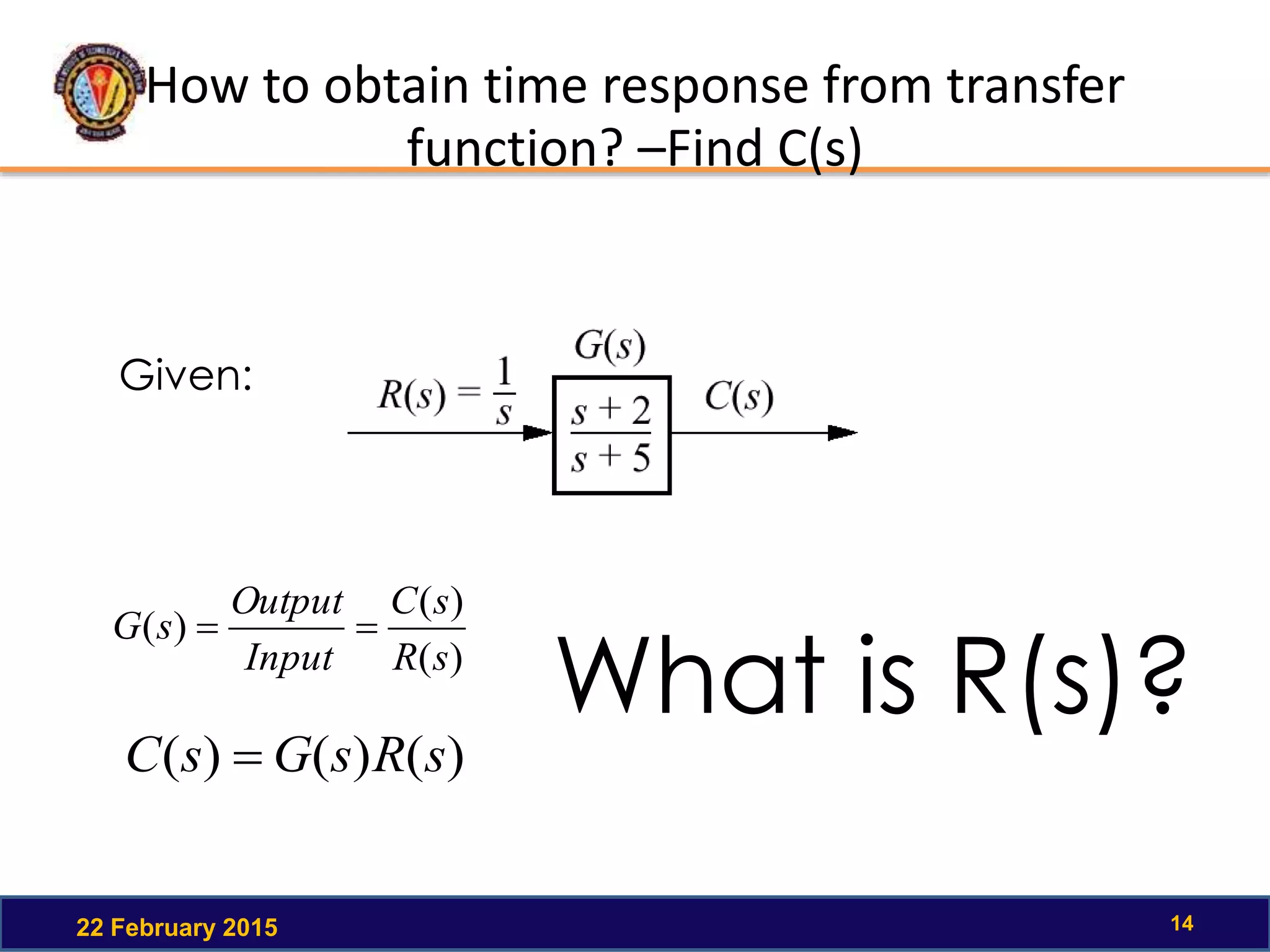
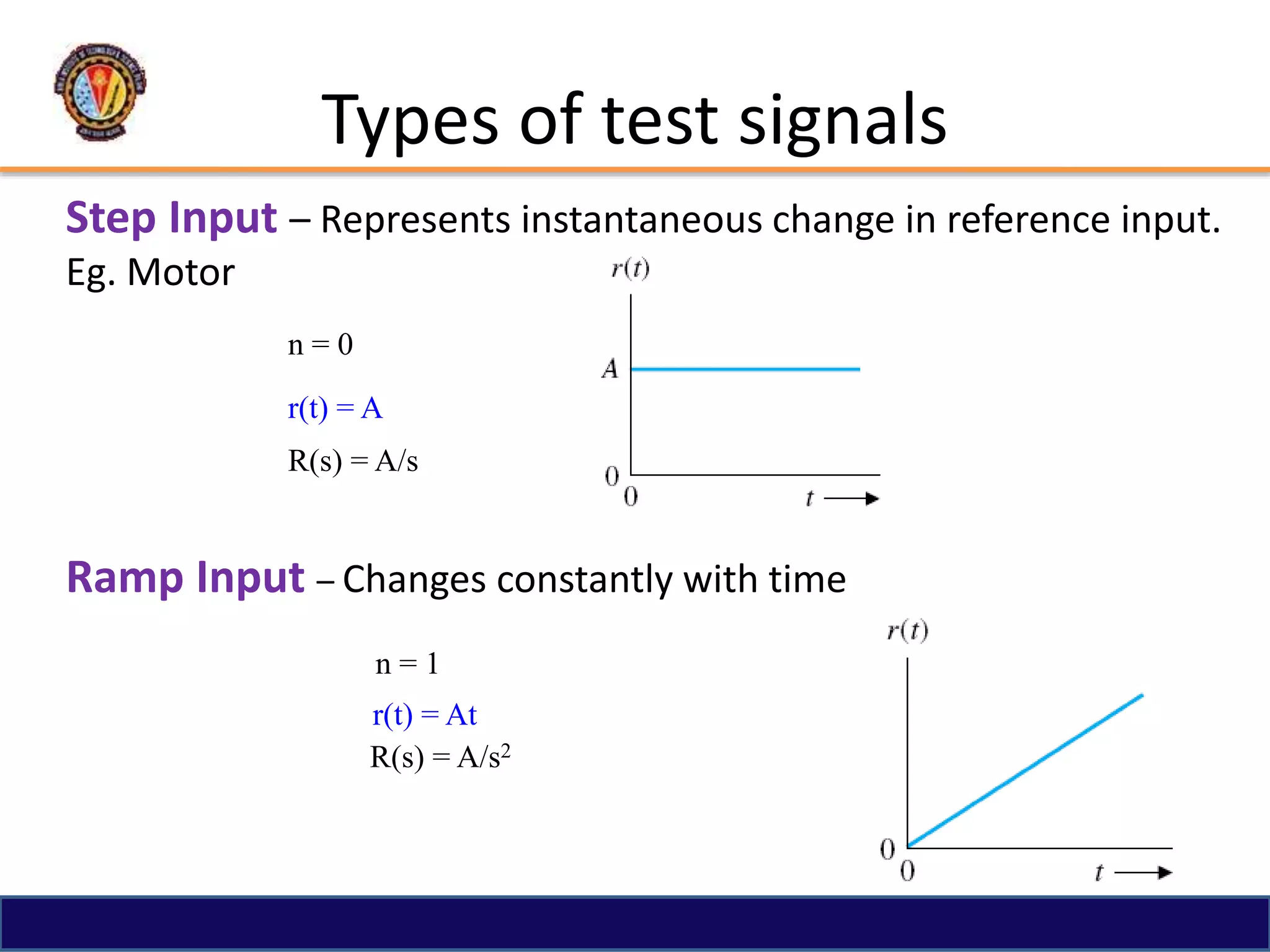
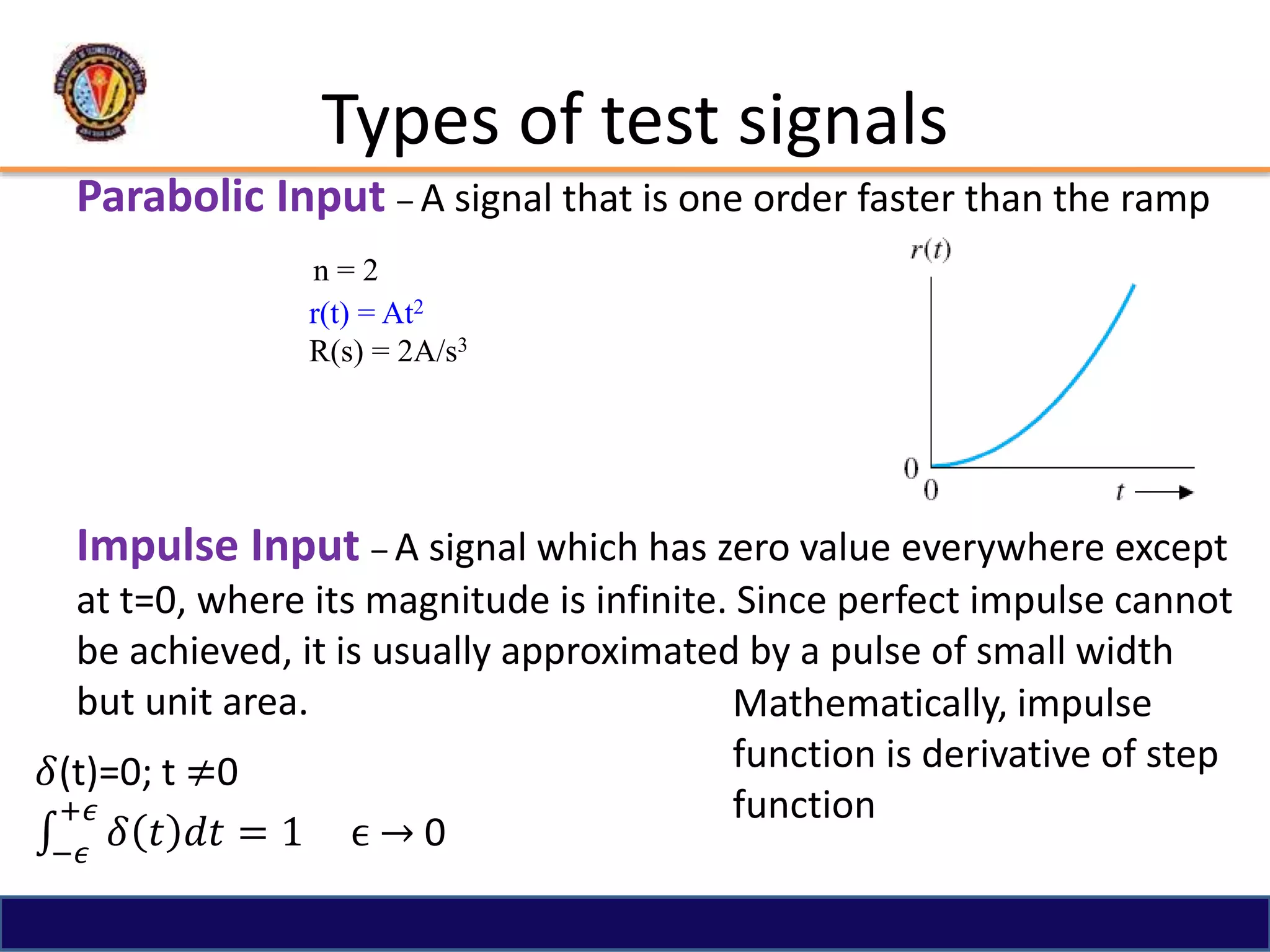
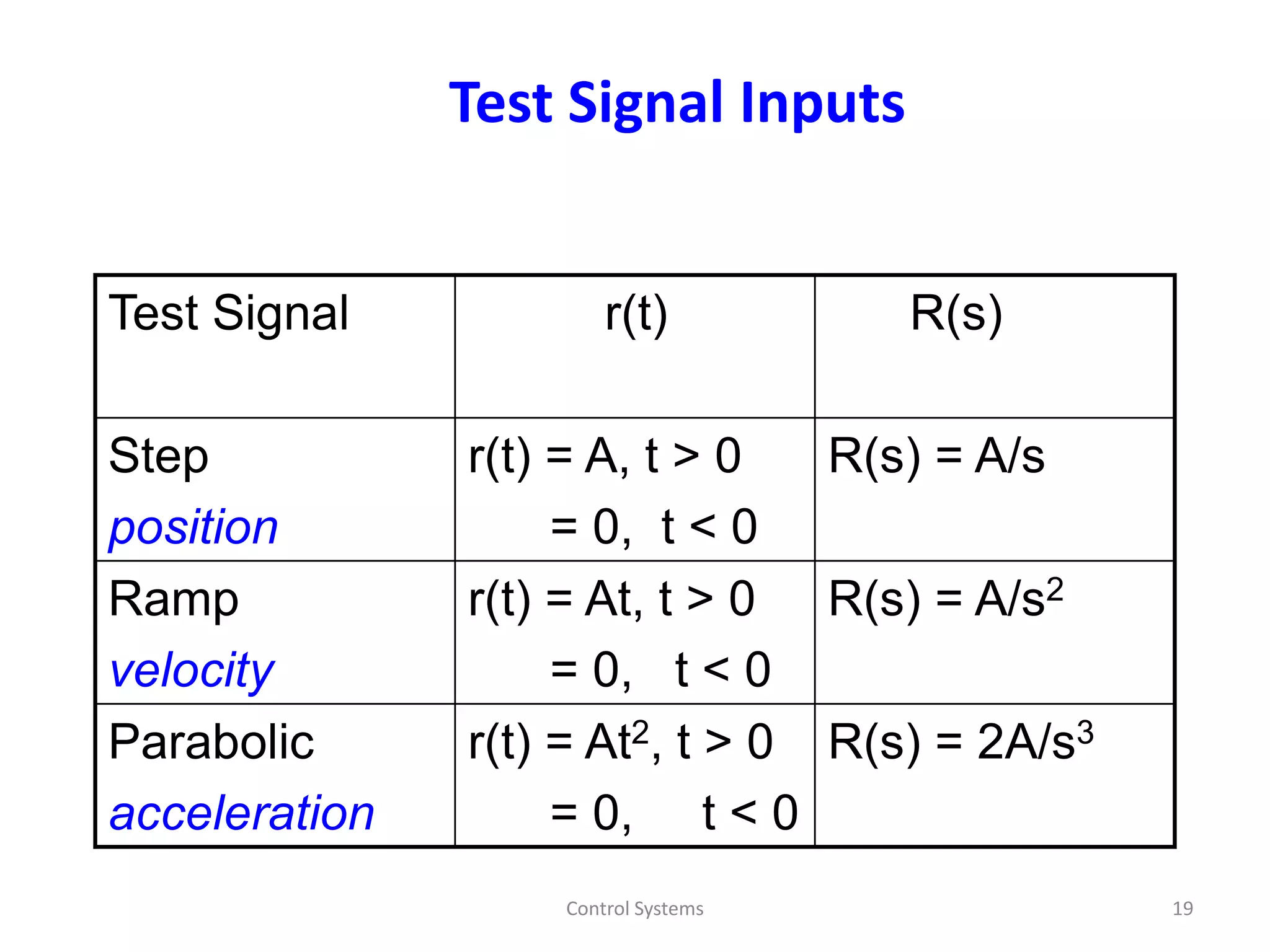
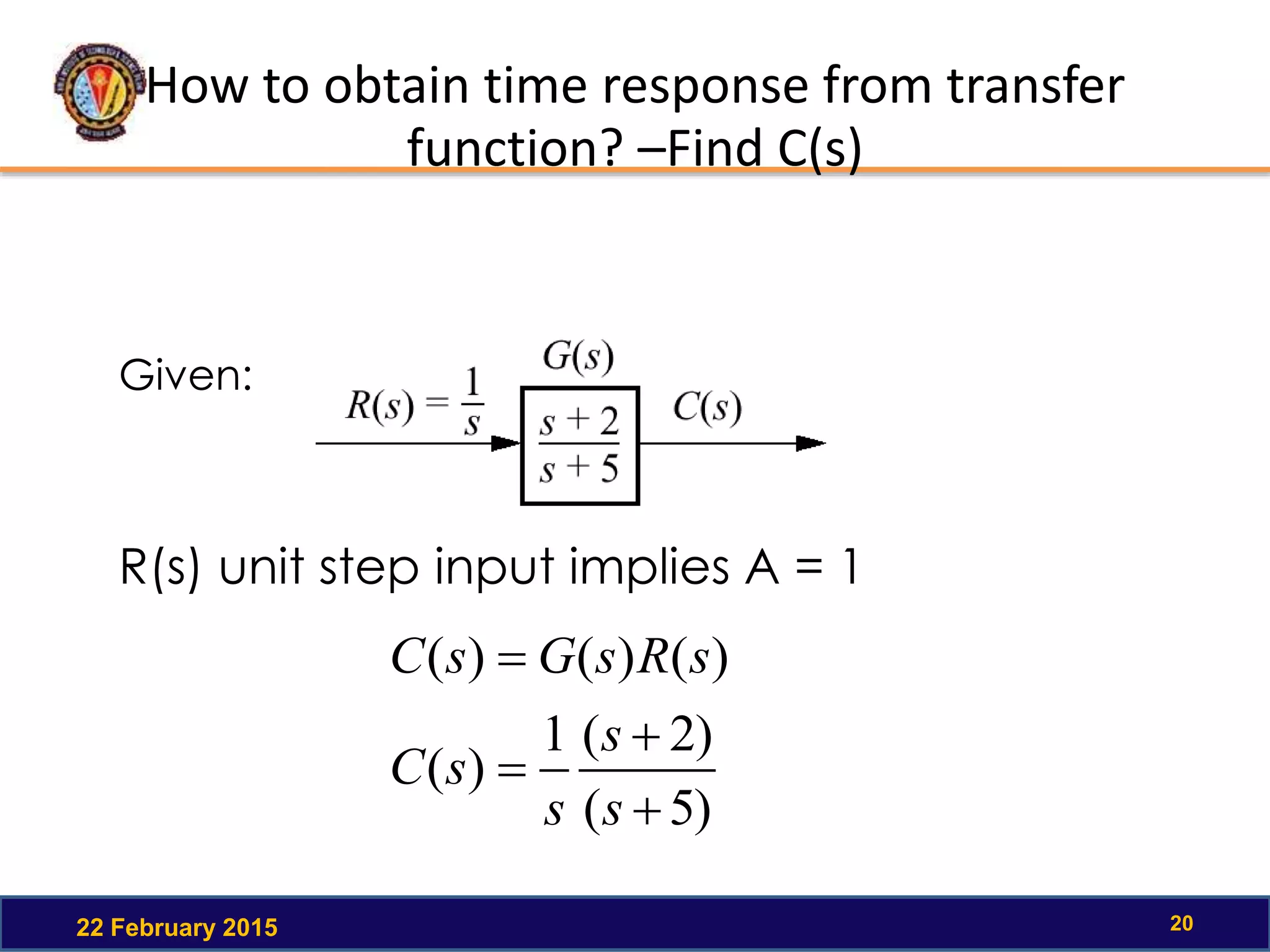
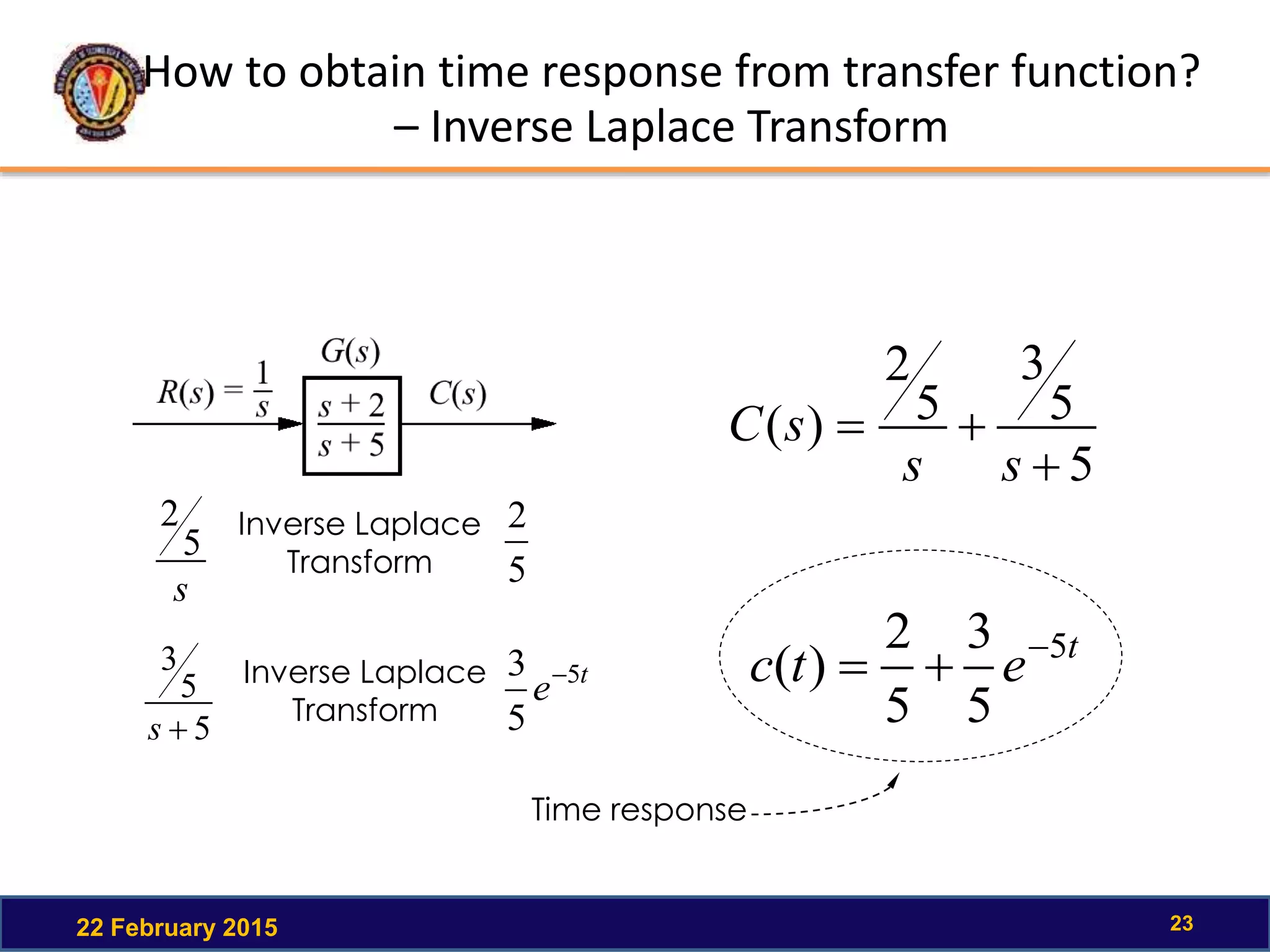
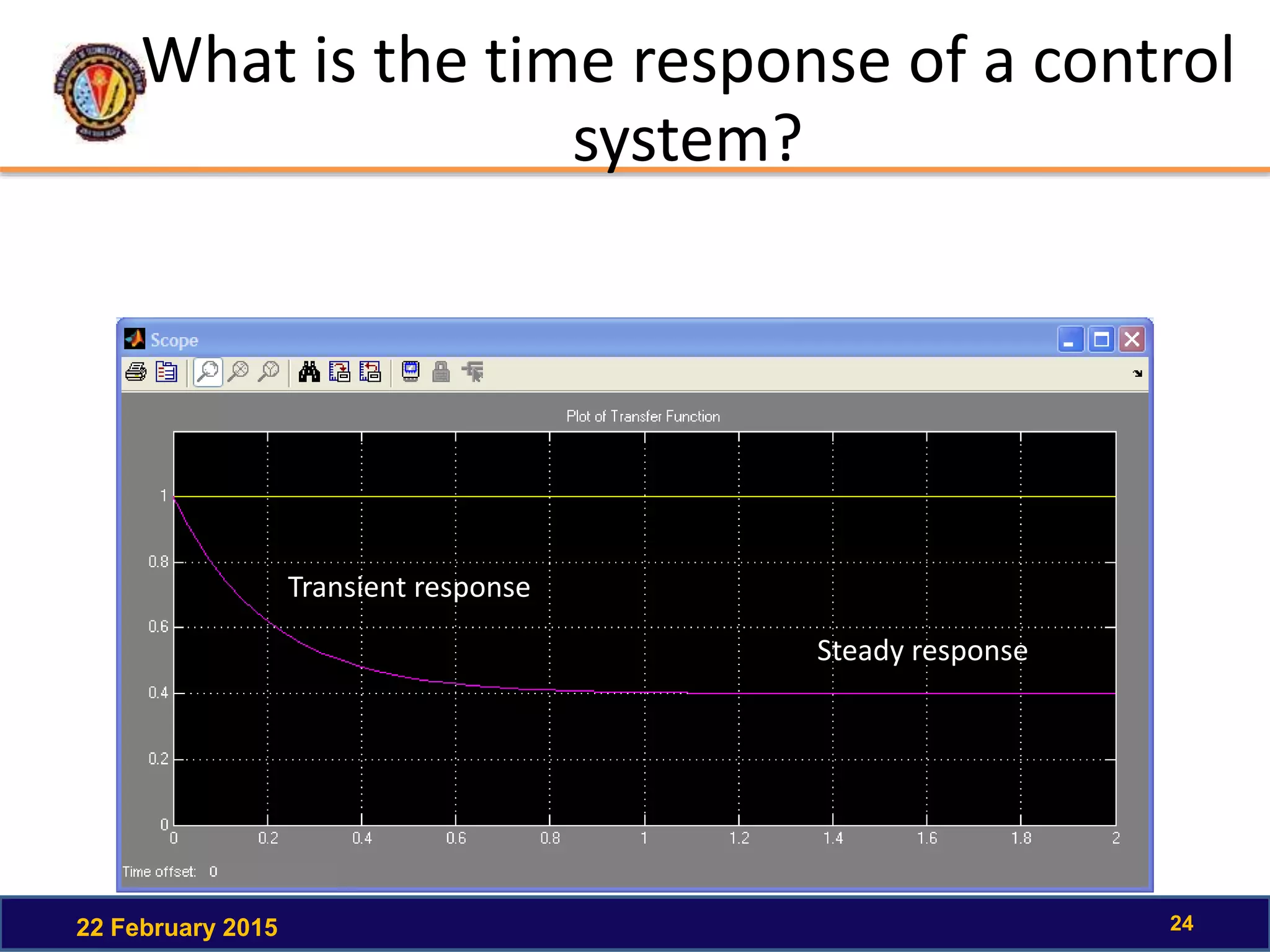
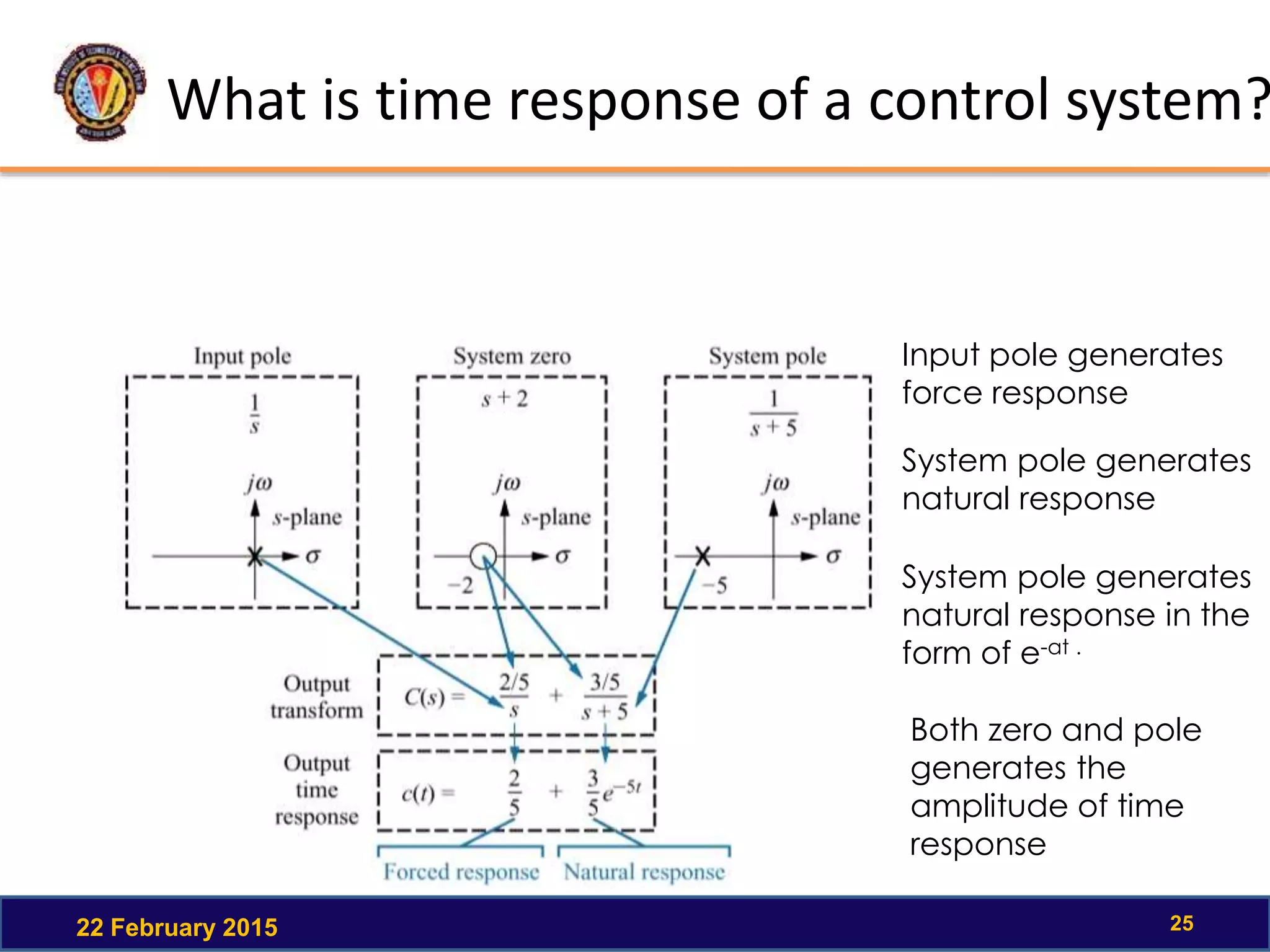
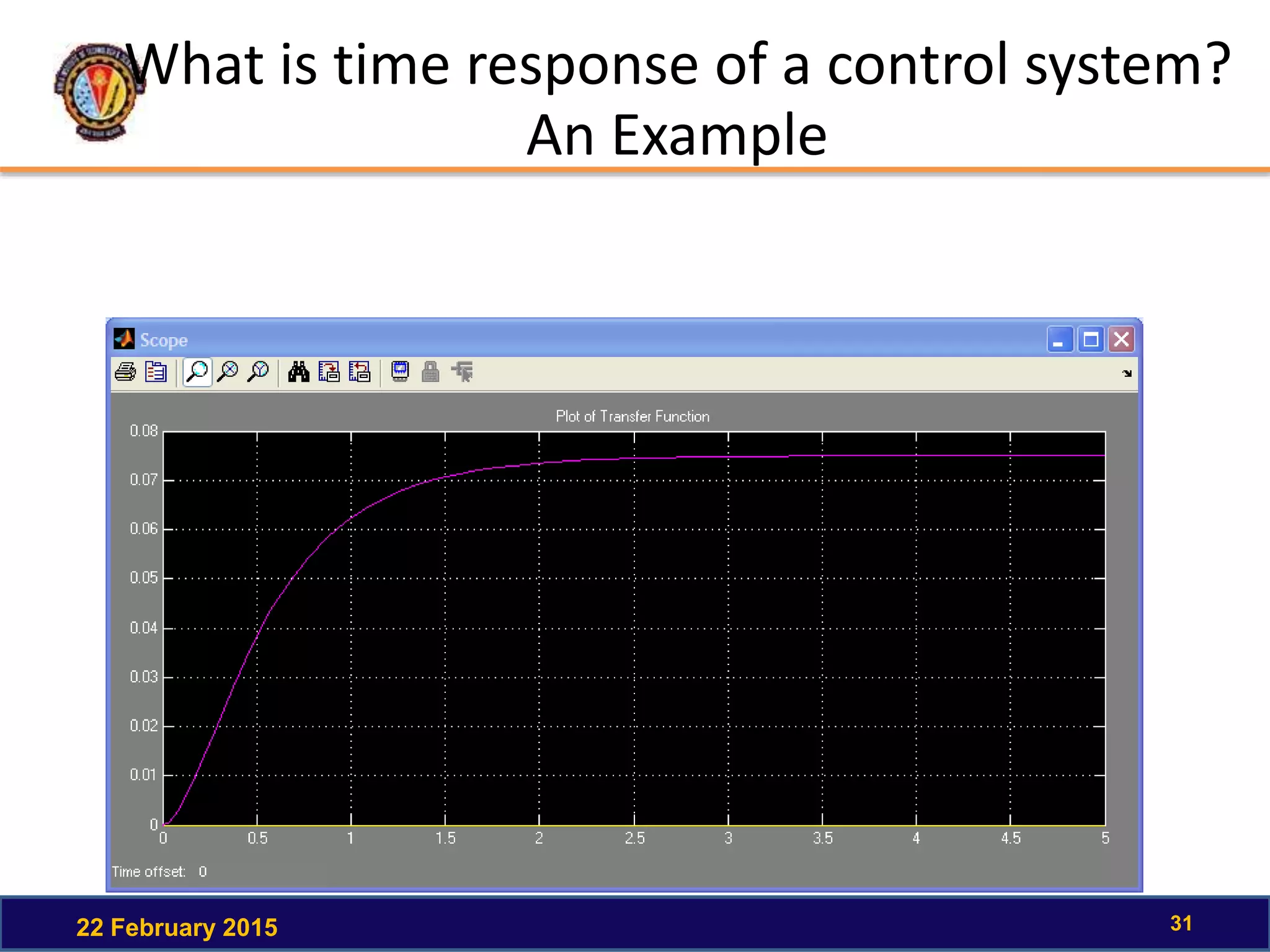
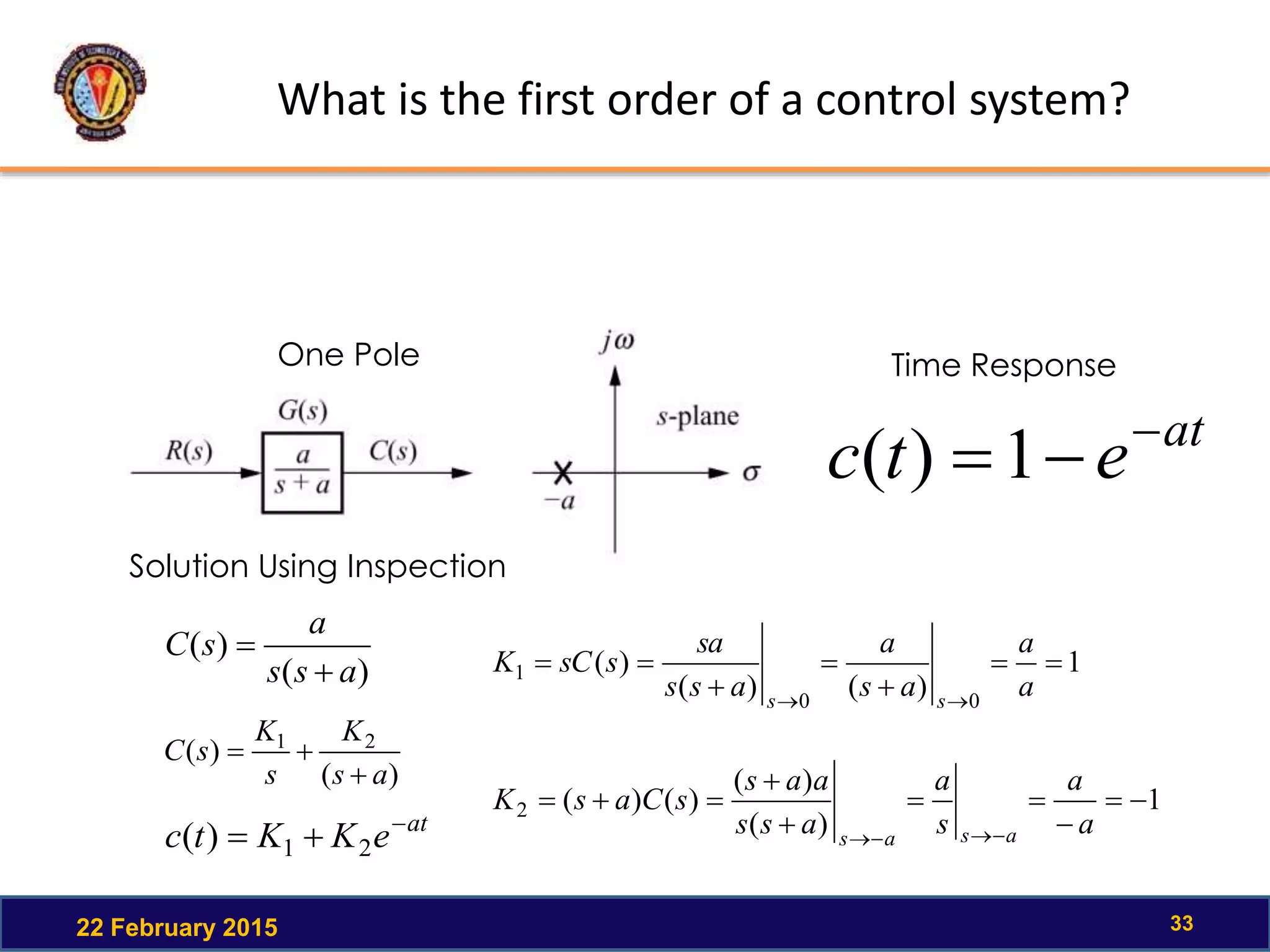
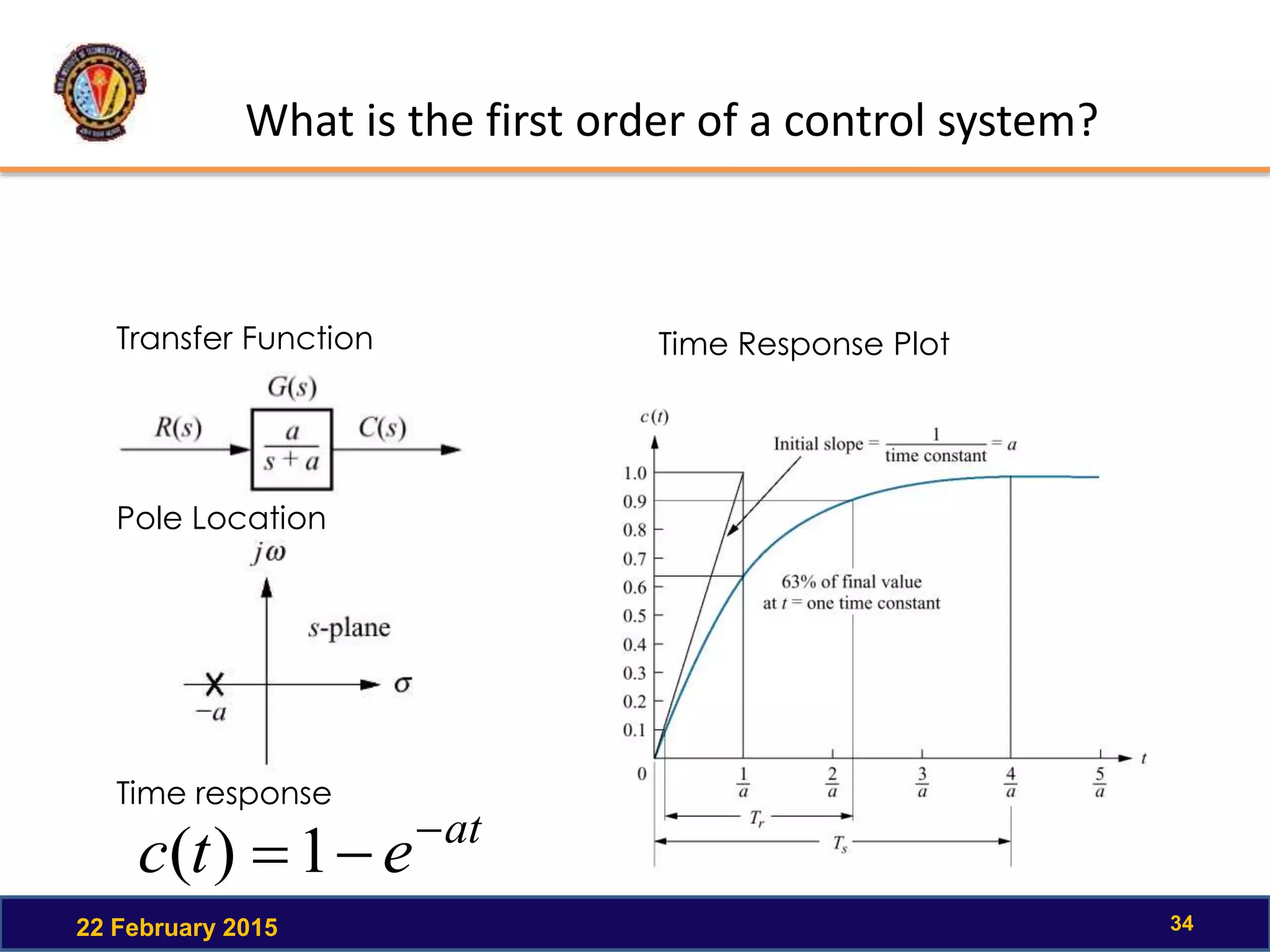
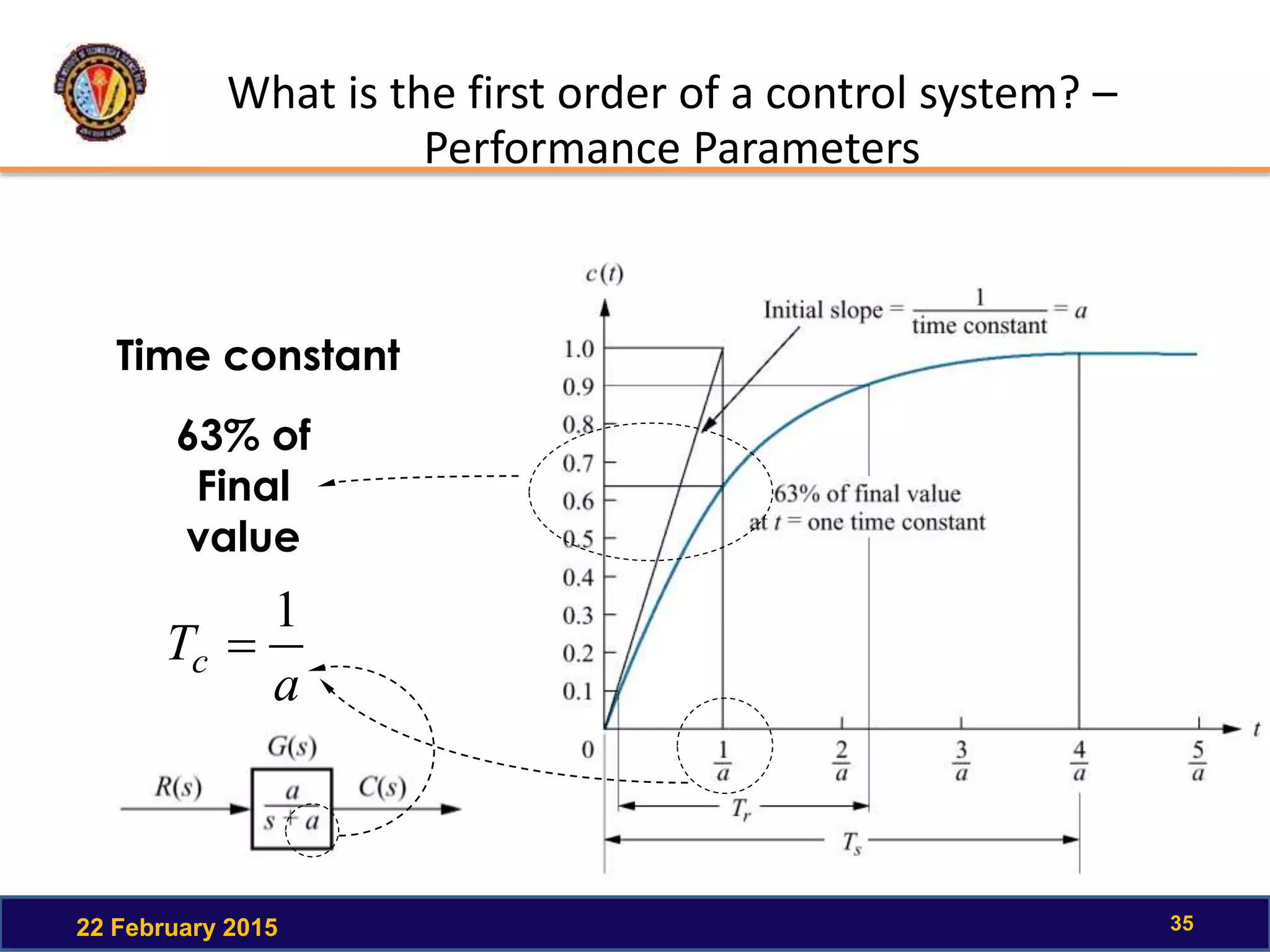
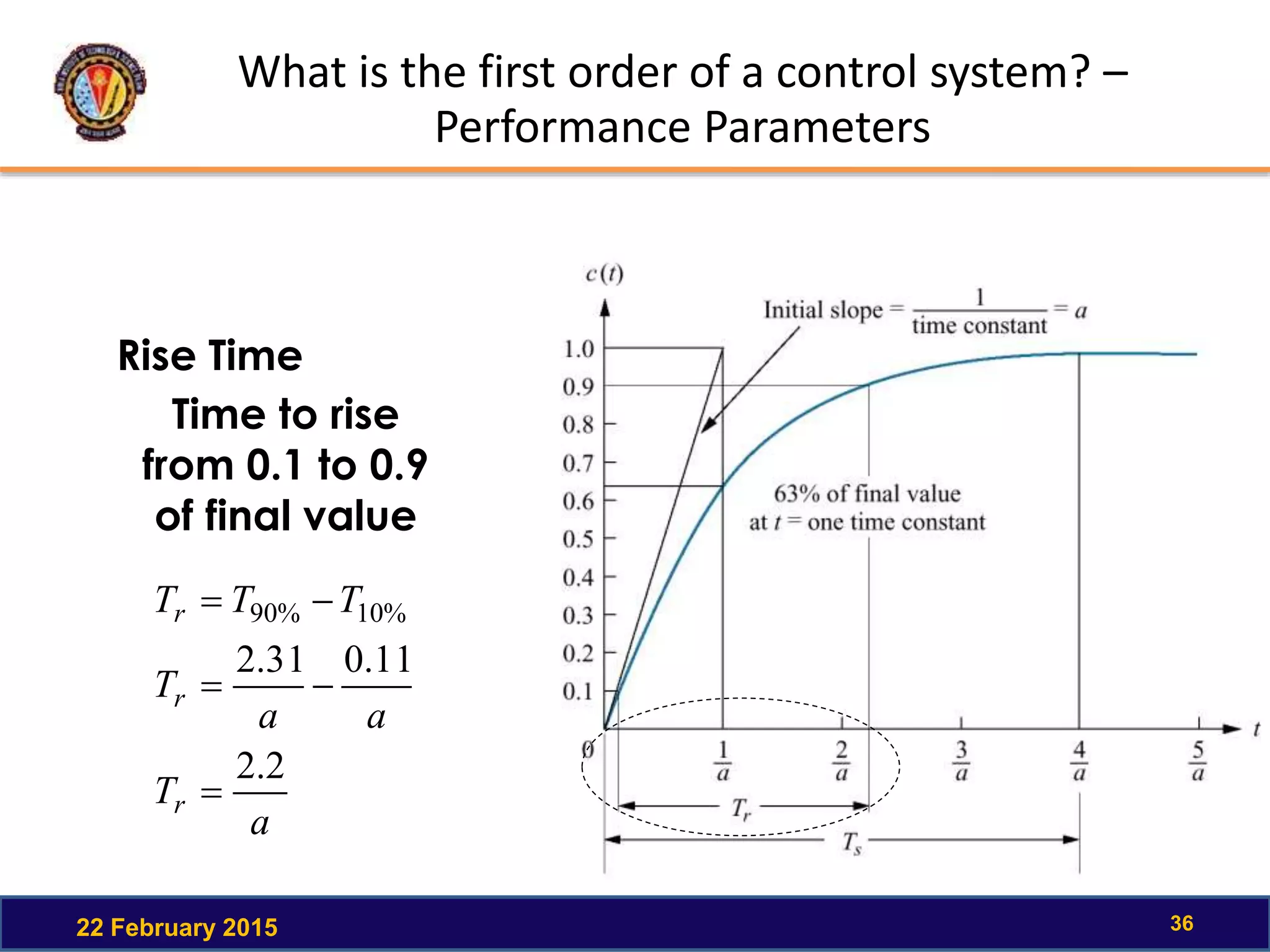
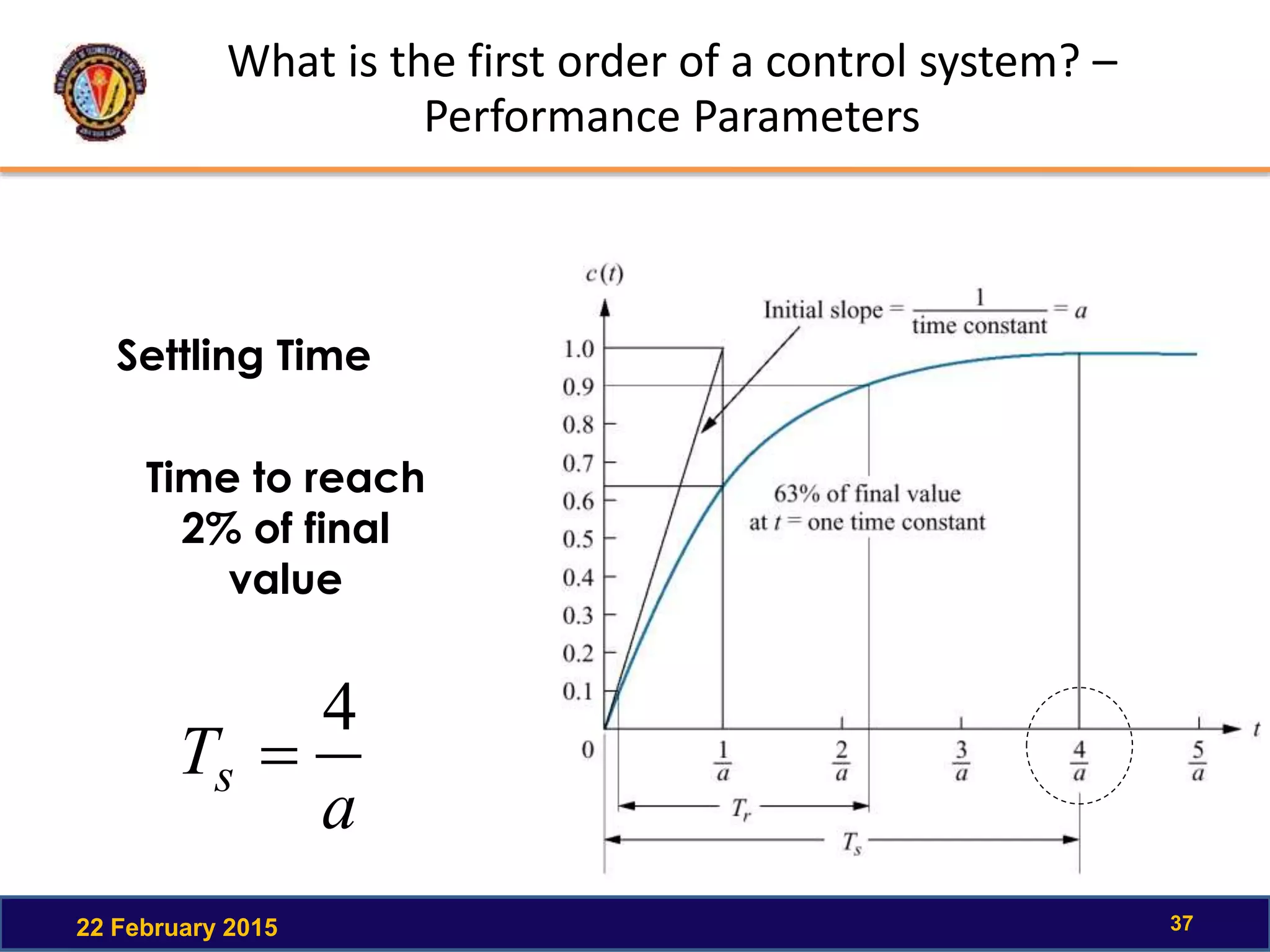
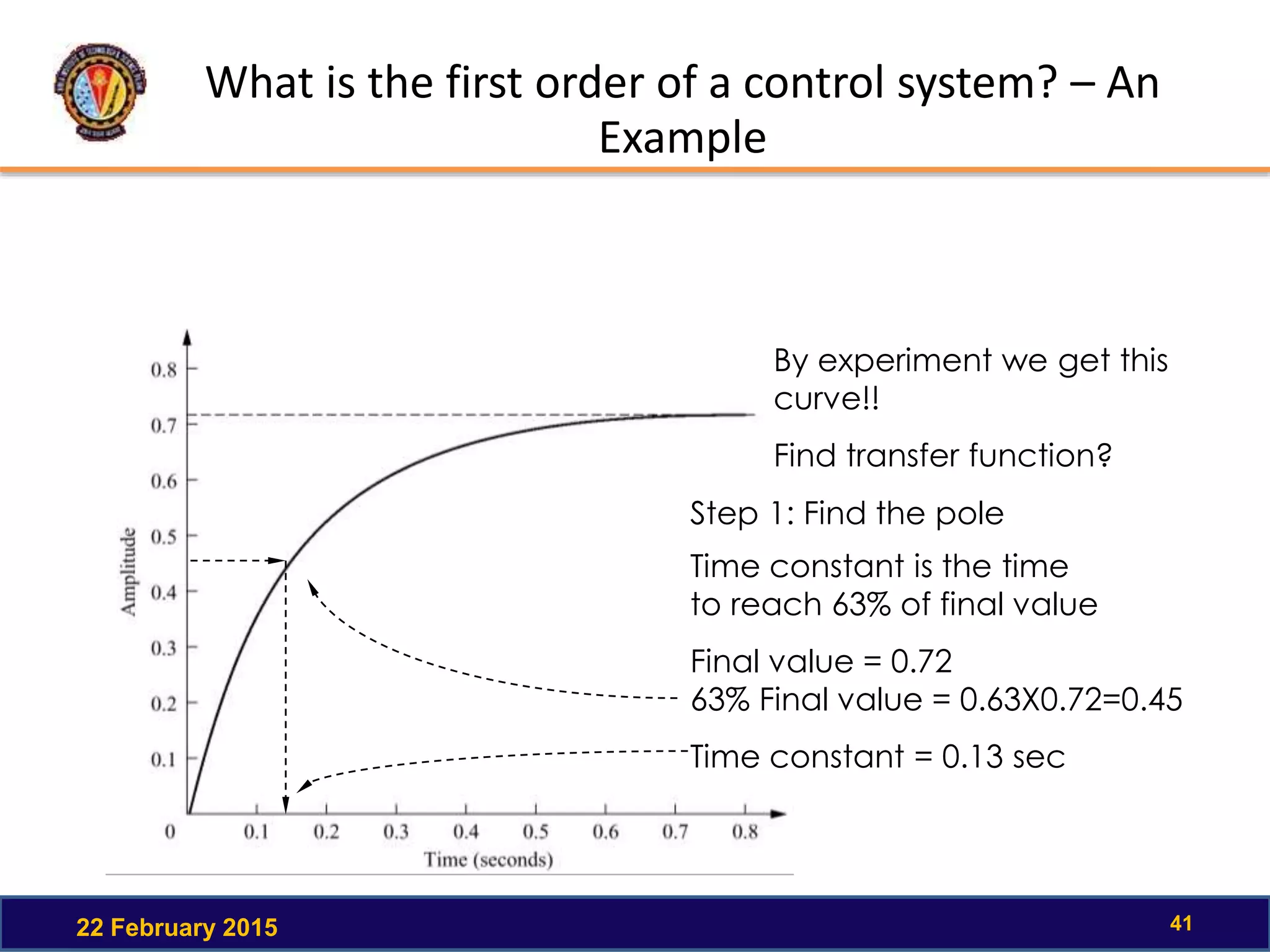
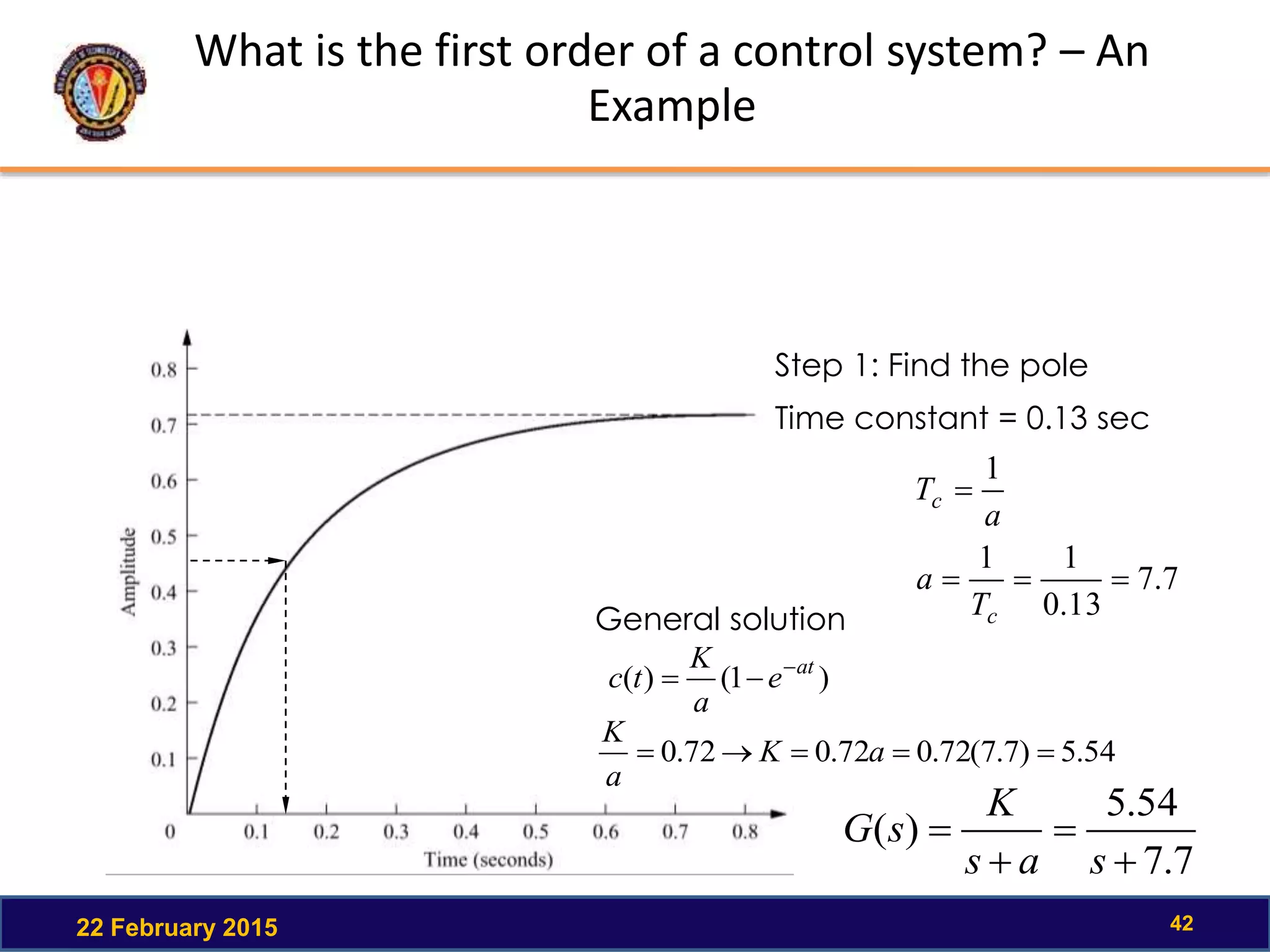
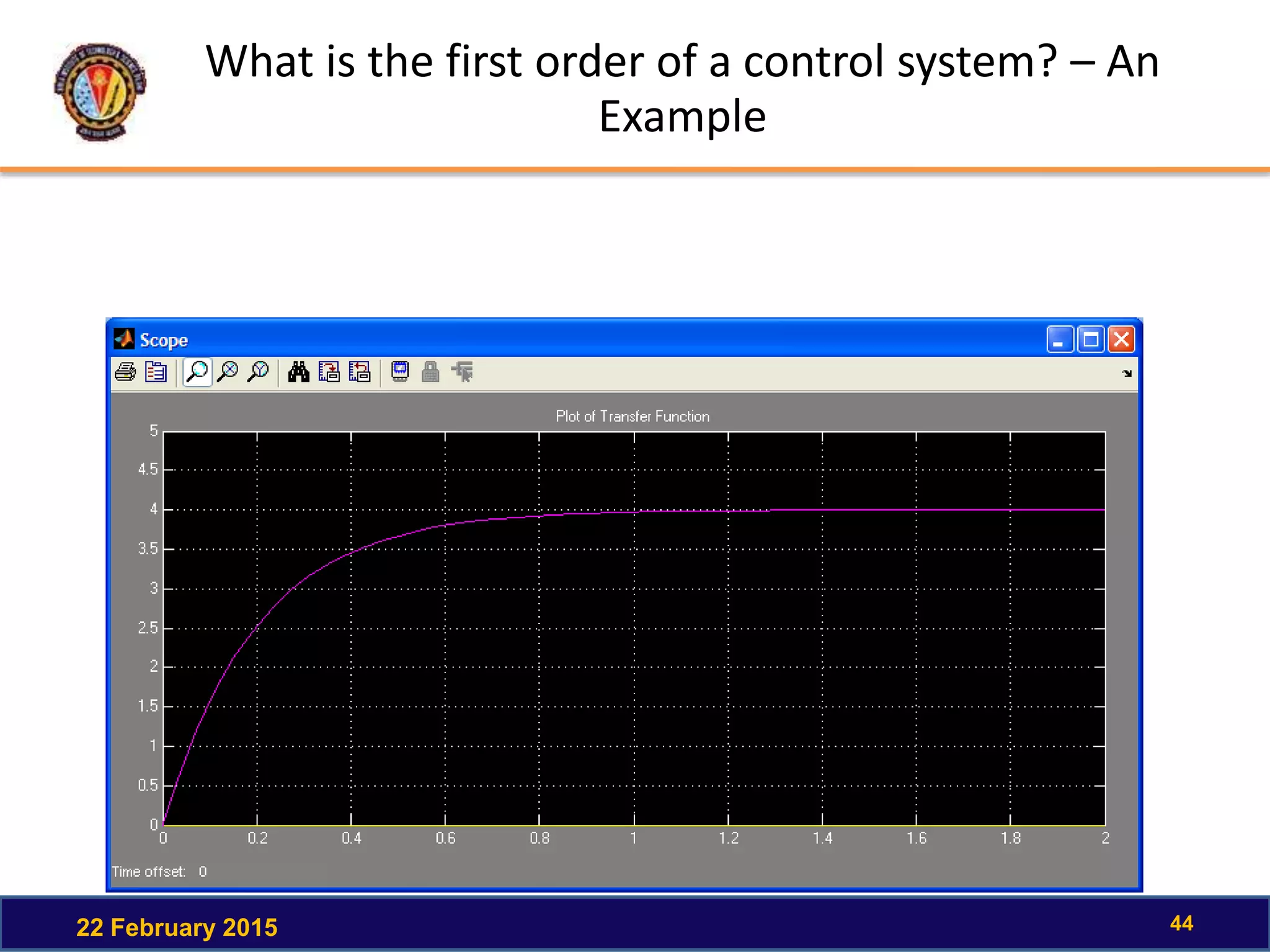
The document discusses the time response of first order systems. It defines time response as the solution to a differential equation over time. Time response consists of the natural response and forced response, and is characterized by transient and steady-state responses on a time response plot. The time constant of a first order system is the time it takes to reach 63% of its final value. Transfer functions can be used to find the system's poles and zeros, which indicate the time response.

1. Time Response of First Order
System
22 February 20151
Madhuri Bayya

2. What is the time response of a control system?
22 February 2015 2
Time response:
The time solution to
differential equation.

3. What is the time response of a control system?
22 February 2015 3
Time response consists of:
1.Natural response
2.Forced response

4. What is the time response of a control system?
22 February 2015 4
Time response Plot
Forced response or
Transient response
Steady-state
response
Time solution to
differential equation
Caused by
the input

5. How to obtain time response?
22 February 2015 5
Schematic
M
)(tf
xM
Kx
)(tfKxxM 
Differential Equation
)(2
sFKXMXs 
Laplace Transform
Time Response
Why
Transfer
Function?
Transfer Function
KMssF
sX
sG

 2
1
)(
)(
)(

6. How to obtain time response?
22 February 2015 6
Why use Transfer Function?
1.Solution by inspection
2.Qualitative solution

7. How to obtain time response from transfer
function?
22 February 2015 7
Given:
How to obtain the time response?
First, we need to understand the
concept of poles and zeros

8. How to obtain time response from transfer
function?
22 February 2015 8
First rule:
The values of Laplace transform variable,
s, that cause the transfer function to
become infinite.
Second rule:
Any roots of the denominator of the
transfer function that are common to the
roots of numerator
What are poles ?

9. How to obtain time response from transfer
function?
22 February 2015 9
Transfer Function
)3)(2)(5(
)3(
)(



sss
s
sG
First rule:
When s = -5, or s = -2 or s = -3, then,
G(s)=infinity! Therefore, the poles
of the transfer function G(s) are -5,
-2 and -3.
)3)(2)(5(
)3(
)(



sss
s
sG
Second rule:
Although the term (s+3) can be
cancelled out, the value -3 is still
the poles of the transfer function
G(s).

10. How to obtain time response from transfer
function?
22 February 2015 10
First rule:
The values of Laplace transform variable,
s, that cause the transfer function to
become zero.
Second rule:
Any roots of the numerator of the transfer
function that are common to roots of the
denominator
What are zeros ?

11. How to obtain time response from transfer
function?
22 February 2015 11
Transfer Function
)3)(2)(5(
)3(
)(



sss
s
sG
First rule:
When s = -3, then, G(s)= 0.
Therefore, the zero of the transfer
function G(s) is -3.
)3)(2)(5(
)3(
)(



sss
s
sG
Second rule:
Although the term (s+3) can be
cancelled out, the value -3 is still
the zero of the transfer function
G(s).

12. How to obtain time response from transfer
function?
22 February 2015 12
Transfer Function
)3)(1)(1(
)7(
)(



sss
s
sG
)9)(2)(11(
)3)(13(
)(



sss
ss
sG
Zero = -7
Poles = -1, -1 and -3
Zero = -13 and -3
Poles = -11, -2 and -9

13. How to obtain time response from transfer
function?
22 February 2015 13
Given:
How to obtain the time response?
1. Find C(s)
2. Expand the transfer function using partial fraction
expansion technique
3. Perform inverse Laplace transform

14. How to obtain time response from transfer
function? –Find C(s)
22 February 2015 14
Given:
)(
)(
)(
sR
sC
Input
Output
sG 
)()()( sRsGsC 
What is R(s)?

15. Test Input Signal
• Unlike electric networks, inputs to many practical
systems are not exactly known ahead of time.
• Difficult to design a control system to satisfy all
possible input signals
• For purpose of analysis and design some basic types
of test inputs assumed, so that performance can be
evaluated.
• Gives an idea of response to other complex inputs.
• Response of complex signals can be determined by
superimposing those due to simple test signals
15Control Systems

16. General form of the standard test signals
r(t) = tn
R(s) = n!/sn+1
16Control Systems

17. Types of test signals
Step Input – Represents instantaneous change in reference input.
Eg. Motor
n = 0
r(t) = A
R(s) = A/s
Ramp Input – Changes constantly with time
r(t) = At
n = 1
R(s) = A/s2

18. Types of test signals
Parabolic Input – A signal that is one order faster than the ramp
n = 2
r(t) = At2
R(s) = 2A/s3
Impulse Input – A signal which has zero value everywhere except
at t=0, where its magnitude is infinite. Since perfect impulse cannot
be achieved, it is usually approximated by a pulse of small width
but unit area.
𝛿(t)=0; t ≠0
−𝜖
+𝜖
𝛿 𝑡 𝑑𝑡 = 1 ϵ → 0
Mathematically, impulse
function is derivative of step
function

19. Test Signal Inputs
Test Signal r(t) R(s)
Step
position
r(t) = A, t > 0
= 0, t < 0
R(s) = A/s
Ramp
velocity
r(t) = At, t > 0
= 0, t < 0
R(s) = A/s2
Parabolic
acceleration
r(t) = At2, t > 0
= 0, t < 0
R(s) = 2A/s3
19Control Systems

20. How to obtain time response from transfer
function? –Find C(s)
22 February 2015 20
Given:
R(s) unit step input implies A = 1
)5(
)2(1
)(
)()()(




s
s
s
sC
sRsGsC

21. How to obtain time response from transfer
function? – Expand C(s)
22 February 2015 21
Expand C(s) using Partial Fraction Expansion
Technique
)5(
)2(1
)(



s
s
s
sC
)5(
)2(
5
)(





ss
s
s
B
s
A
sC

22. How to obtain time response from transfer
function? – Expand C(s)
22 February 2015 22
)5(
)2(
5
)(





ss
s
s
B
s
A
sC
5
2
)5(
)2(
0




s
s
s
A
5
3
)(
)2(
5



s
s
s
B
5
5
3
5
2
)(


ss
sC
How to find A
and B?

23. How to obtain time response from transfer function?
– Inverse Laplace Transform
22 February 2015 23
5
5
3
5
2
)(


ss
sC
s
5
2 Inverse Laplace
Transform 5
2
5
5
3
s
Inverse Laplace
Transform
t
e 5
5
3 
t
etc 5
5
3
5
2
)( 

Time response

24. What is the time response of a control
system?
22 February 2015 24
Steady response
Transient response

25. What is time response of a control system?
22 February 2015 25
Input pole generates
force response
System pole generates
natural response
System pole generates
natural response in the
form of e-αt .
Both zero and pole
generates the
amplitude of time
response

26. What is time response of a control system?
An Example
22 February 2015 26
)5)(4)(2(
)3(


sss
s
)(sC
s
sR
1
)( 
By inspection:
)5()4()2(
)( 4321






s
K
s
K
s
K
s
K
sC
What are poles and
zeros?
Poles = -2, -4 and -5
Zero = -3
Force
response Natural
response
Influence of poles
on time response

27. What is time response of a control system?
An Example
22 February 2015 27
)5)(4)(2(
)3(


sss
s
)(sC
s
sR
1
)( 
By inspection:
)5()4()2(
)( 4321






s
K
s
K
s
K
s
K
sC
Inverse Laplace
Transform
ttt
eKeKeKKtc 5
4
4
3
2
21)( 

Time response – solution to differential equation

28. What is time response of a control system?
An Example
22 February 2015 28
)5()4()2(
)( 4321






s
K
s
K
s
K
s
K
sC
ttt
eKeKeKKtc 5
4
4
3
2
21)( 

How to
evaluate K1,
K2, K3 and K4?
)5)(4)(2(
)3(
)(



ssss
s
sC
11
3
)5)(4)(2(
)3(
)5)(4)(2(
)3(
)(
00
1 






 ss
sss
s
ssss
ss
KssC

29. What is time response of a control system?
An Example
22 February 2015 29
40
3
)50)(40)(20(
30
)5)(4)(2(
)3(
)5)(4)(2(
)3(
)(
00
1 









 ss
sss
s
ssss
ss
KssC
12
1
)52)(42(2
)32(
)5)(4(
)3(
)5)(4)(2(
)3)(2(
)()2(
22
2











 ss
sss
s
ssss
ss
KsCs
8
1
)54)(24)(4(
)34(
)5)(2(
)3(
)5)(4)(2(
)3)(4(
)()4(
44
1











 ss
sss
s
ssss
ss
KsCs
15
2
)45)(25(5
)35(
)4)(2(
)3(
)5)(4)(2(
)3)(5(
)()5(
55
1












 ss
sss
s
ssss
ss
KsCs

30. What is time response of a control system?
An Example
22 February 2015 30
ttt
eKeKeKKtc 5
4
4
3
2
21)( 

ttt
eeetc 54
3
2
15
2
8
1
12
1
40
3
)( 


31. What is time response of a control system?
An Example
22 February 2015 31

32. What is the order of a control system?
22 February 2015 32
The highest
order of
differential
equations
The number
of poles

33. What is the first order of a control system?
22 February 2015 33
Solution Using Inspection
at
eKKtc 
 21)(
)(
)(
ass
a
sC


)(
)( 21
as
K
s
K
sC


1
)()(
)(
00
1 





a
a
as
a
ass
sa
ssCK
ss
1
)(
)(
)()(2 






a
a
s
a
ass
aas
sCasK
asas
at
etc 
1)(
One Pole Time Response

34. What is the first order of a control system?
22 February 2015 34
at
etc 
1)(
Transfer Function
Pole Location
Time response
Time Response Plot

35. What is the first order of a control system? –
Performance Parameters
22 February 2015 35
Time constant
a
Tc
1

63% of
Final
value

36. What is the first order of a control system? –
Performance Parameters
22 February 2015 36
Rise Time
a
T
aa
T
TTT
r
r
r
2.2
11.031.2
%10%90



Time to rise
from 0.1 to 0.9
of final value

37. What is the first order of a control system? –
Performance Parameters
22 February 2015 37
Settling Time
a
Ts
4

Time to reach
2% of final
value

38. What is the first order of a control system? –
Performance Parameters
22 February 2015 38
Settling Time
a
Ts
4

Time to reach
2% of final value
Rise Time
a
Tr
2.2

Time to rise from
0.1 to 0.9 of final
value
Time constant
a
Tc
1

63% of Final
value

39. What is the first order of a control system? – An
Example
22 February 2015 39
Settling Time
sec
50
44

a
Ts
Rise Time
sec
50
2.22.2

a
Tr
Time constant
sec
50
11

a
Tc50
50
)(


s
sG
First Order because one
pole: pole = a = -50
t
etc 50
1)( 

By inspection the solution of
unit step input is:
s
sR
1
)( 

40. What is the first order of a control system? – An
Example
22 February 2015 40
50
200
)(


s
sG
)1(4)( 50t
etc 

By inspection the solution of
unit step input is:
s
sR
1
)( 
But the numerator (200) is
not equal to “a” (50).
50
50
4)(


s
sG
In general:
as
K
sG

)( )1()( at
e
a
K
tc 

Notice that time constant, rise
time and settling time are still the
same. The performances only
depend on the pole.
a
Ts
4

a
Tr
2.2

a
Tc
1


41. What is the first order of a control system? – An
Example
22 February 2015 41
By experiment we get this
curve!!
Find transfer function?
Step 1: Find the pole
Time constant is the time
to reach 63% of final value
Final value = 0.72
63% Final value = 0.63X0.72=0.45
Time constant = 0.13 sec

42. What is the first order of a control system? – An
Example
22 February 2015 42
Step 1: Find the pole
Time constant = 0.13 sec
7.7
13.0
11
1


c
c
T
a
a
T
)1()( at
e
a
K
tc 

General solution
54.5)7.7(72.072.072.0  aK
a
K
7.7
54.5
)(




sas
K
sG

43. What is the first order of a control system? – An
Example
22 February 2015 43
5
20
)(


s
sG
What are the time constant, rise time, settling time and
steady-state value?

44. What is the first order of a control system? – An
Example
22 February 2015 44

45. Examples
• Discharge of electronic camera flash
• Flow of fluid form a tank
• Cooling of a cup of coffee
22 February 2015 45