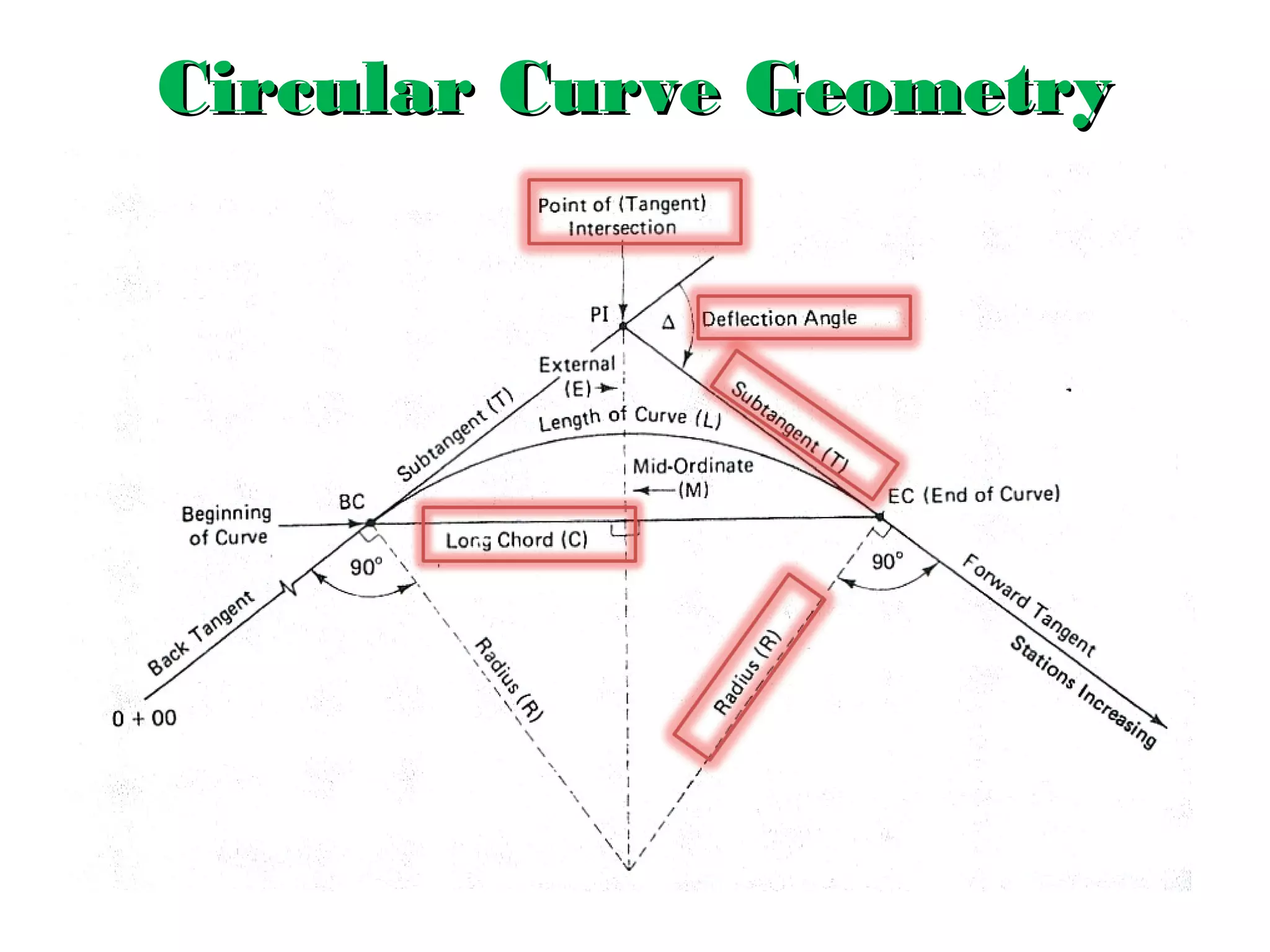
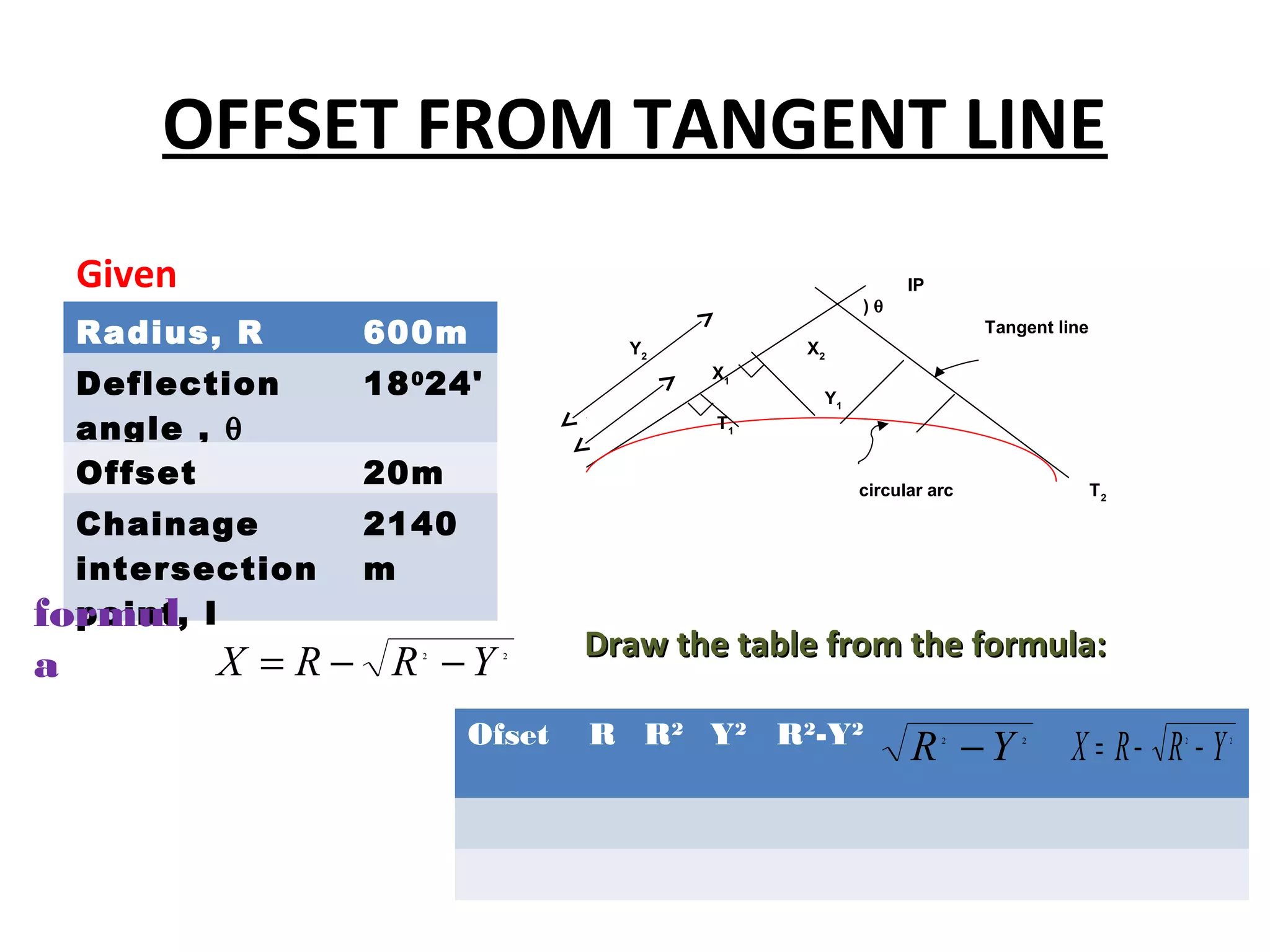
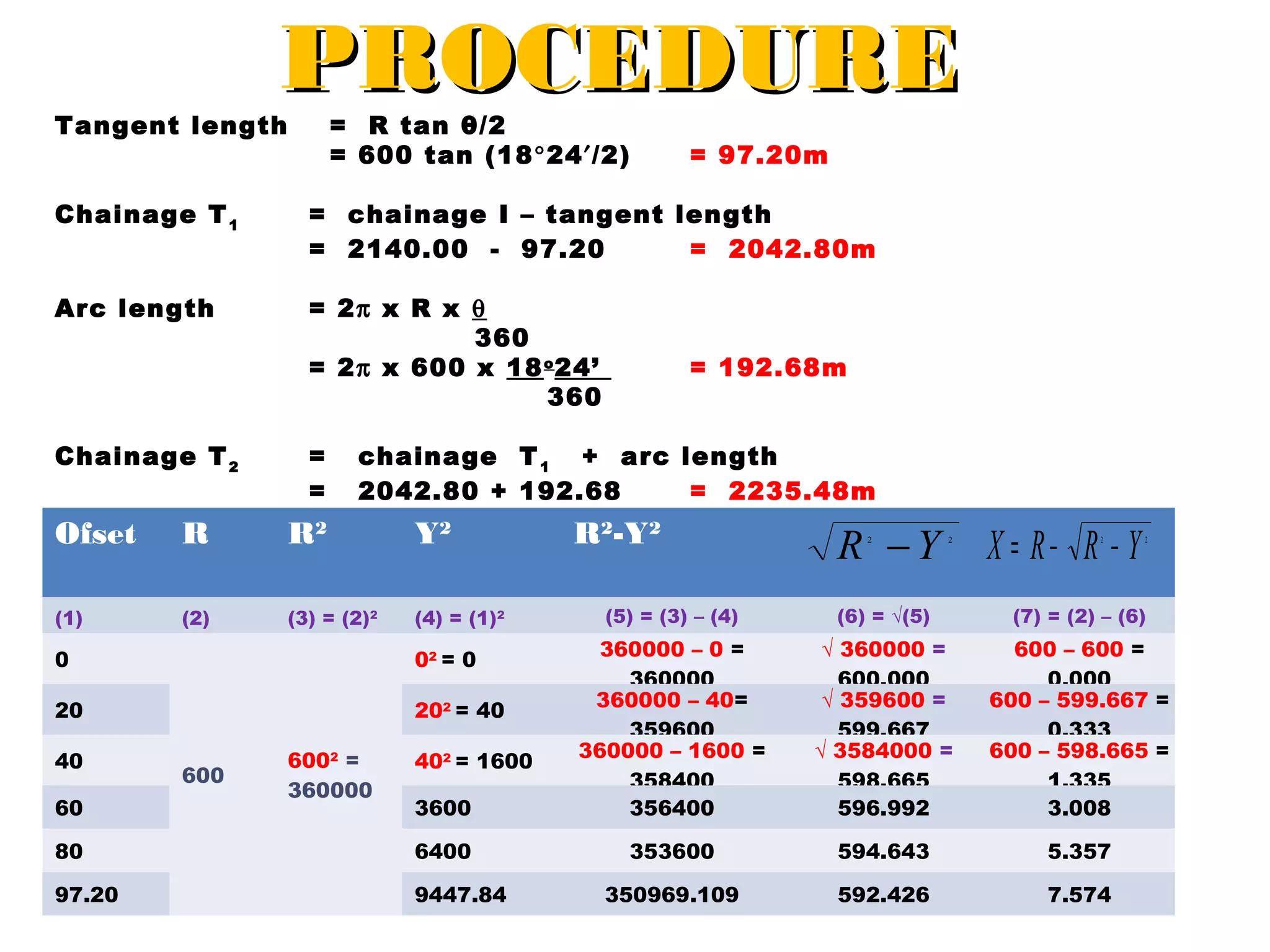
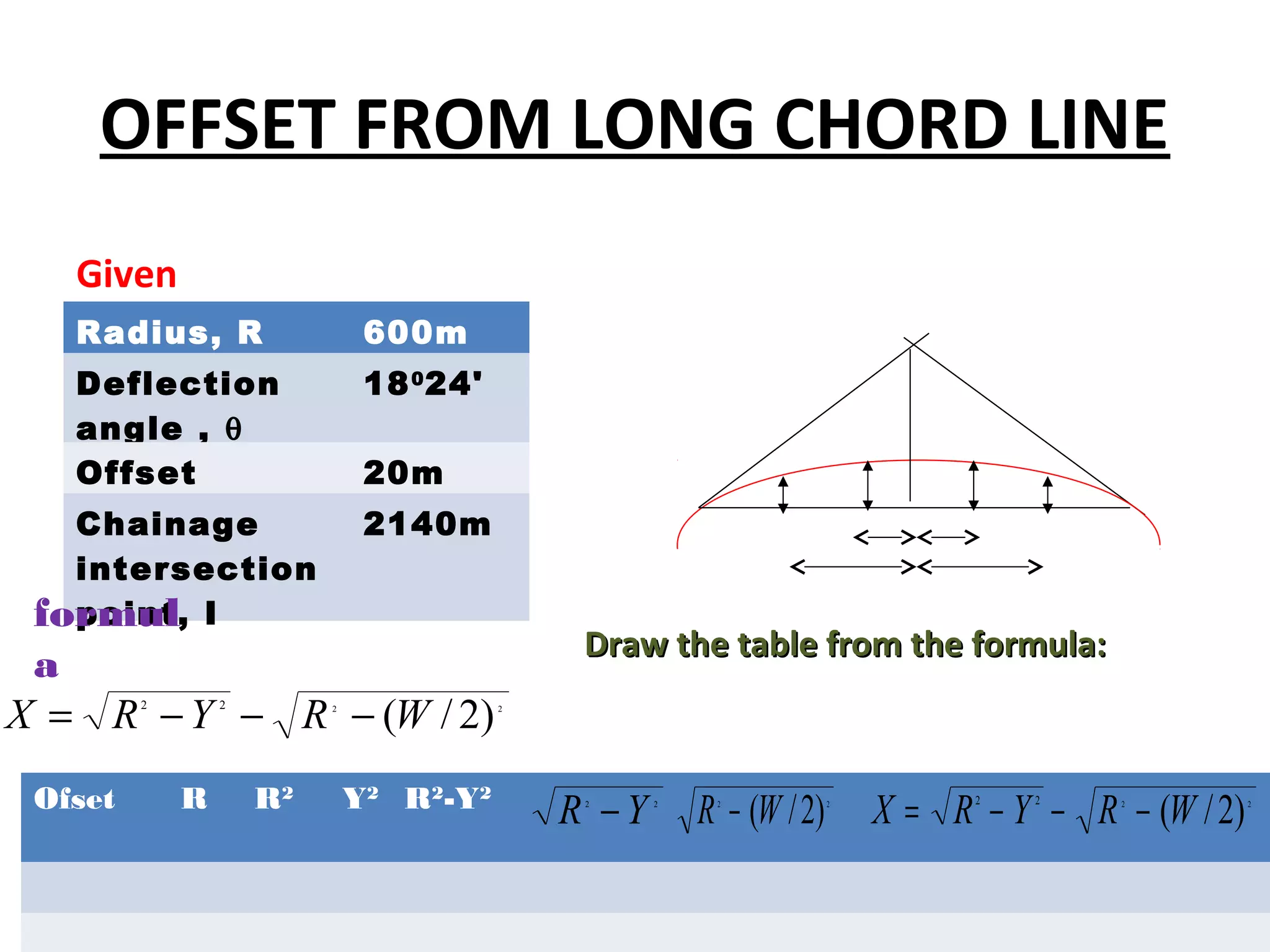
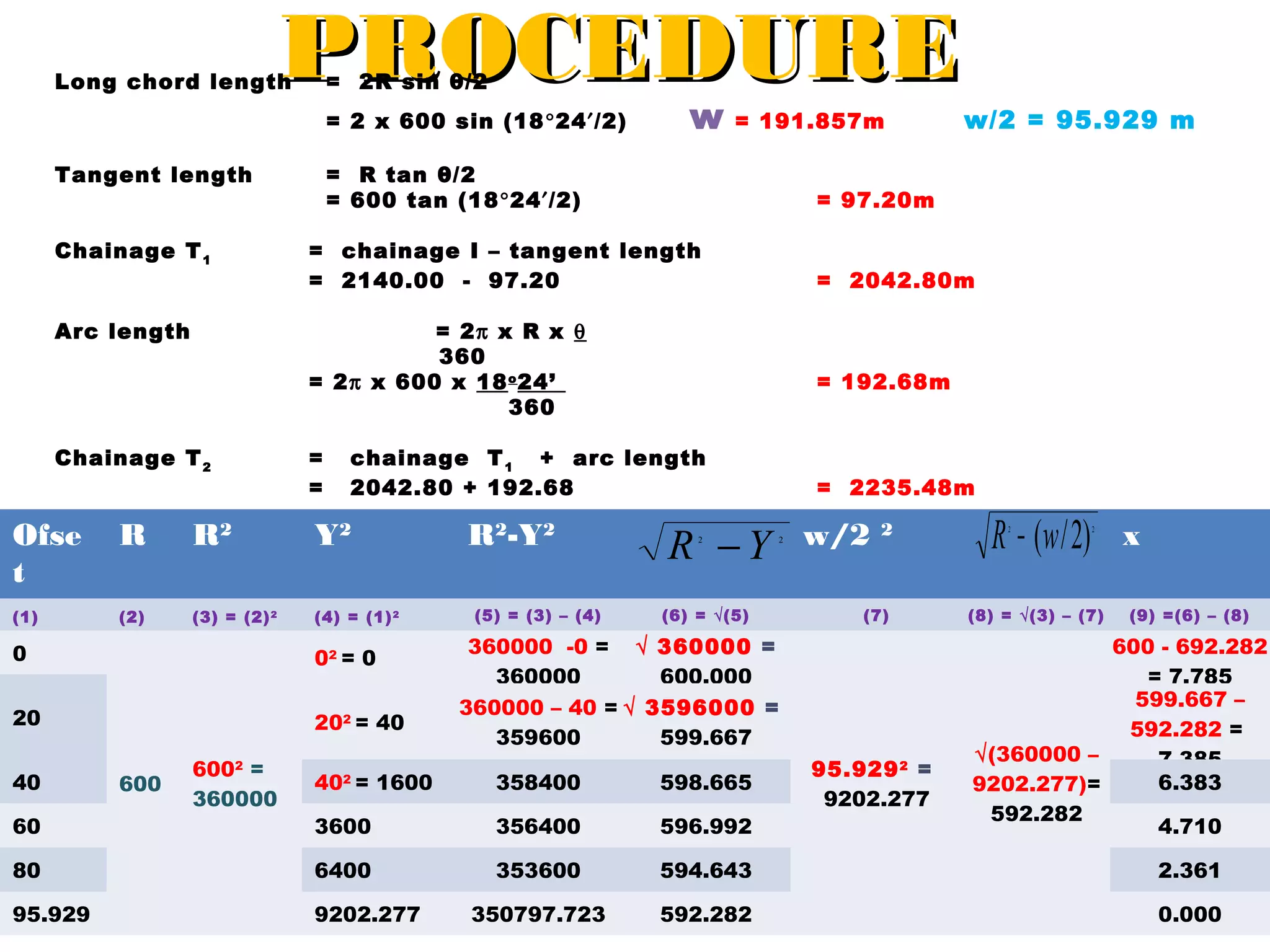
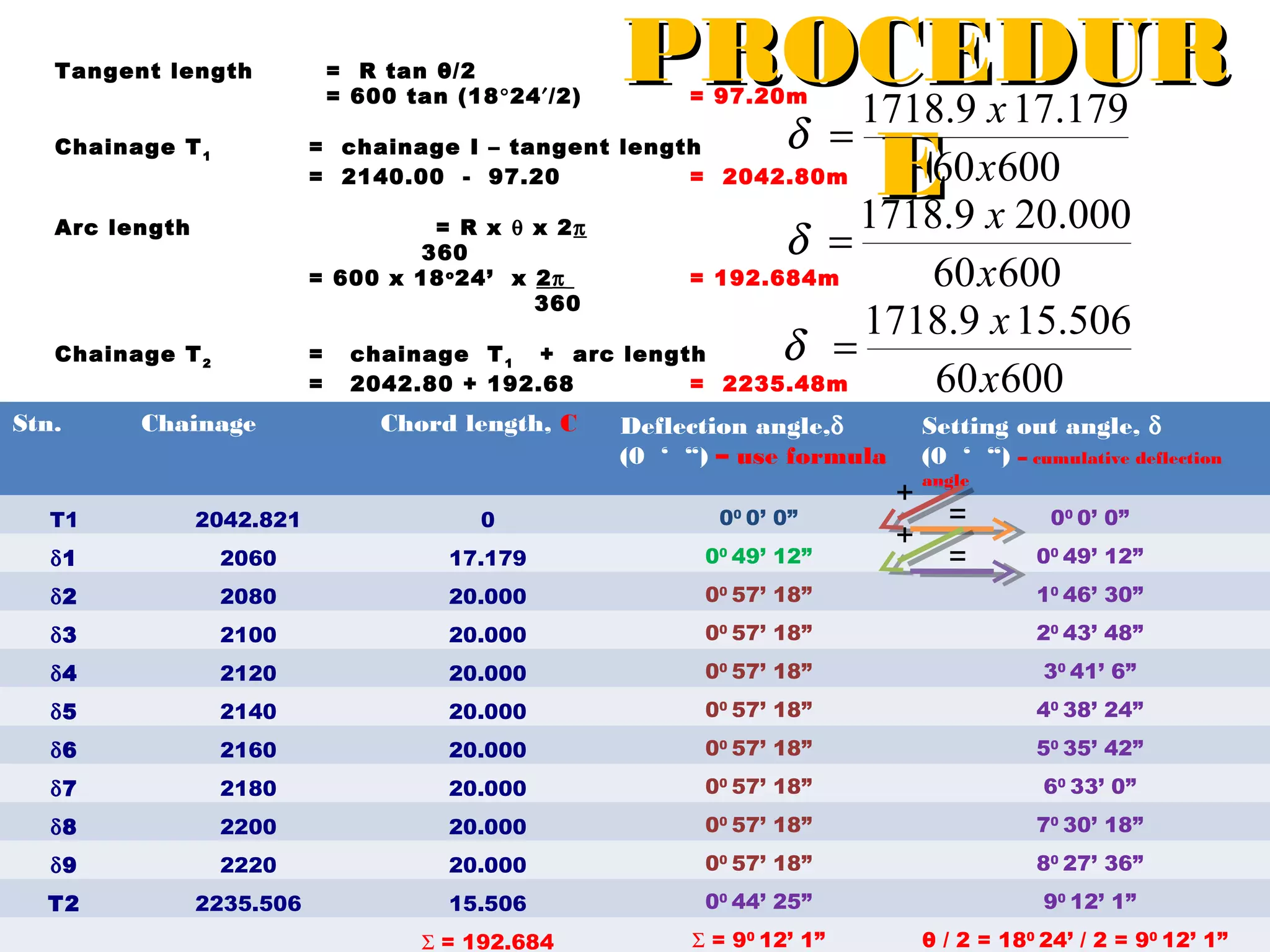
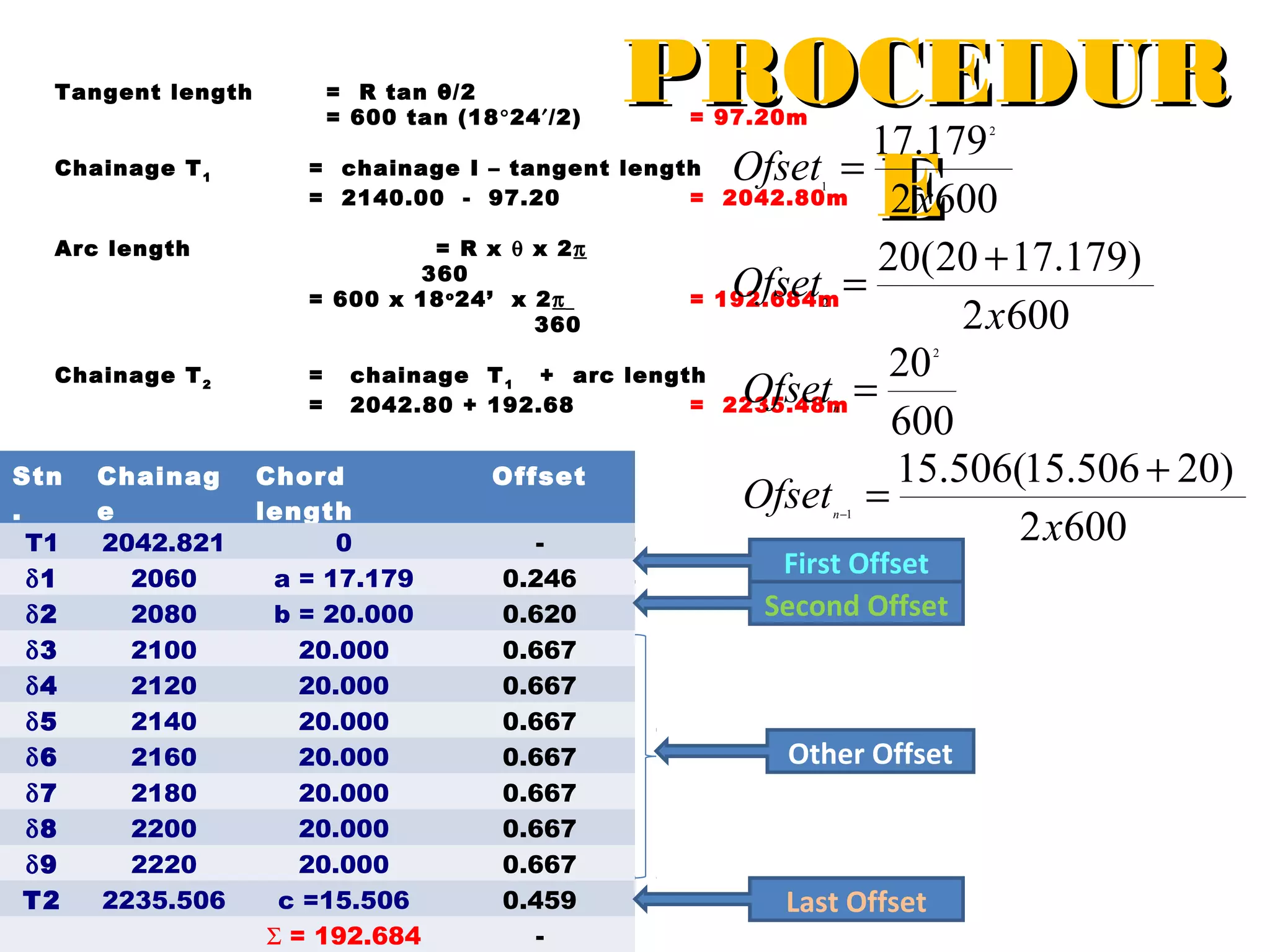
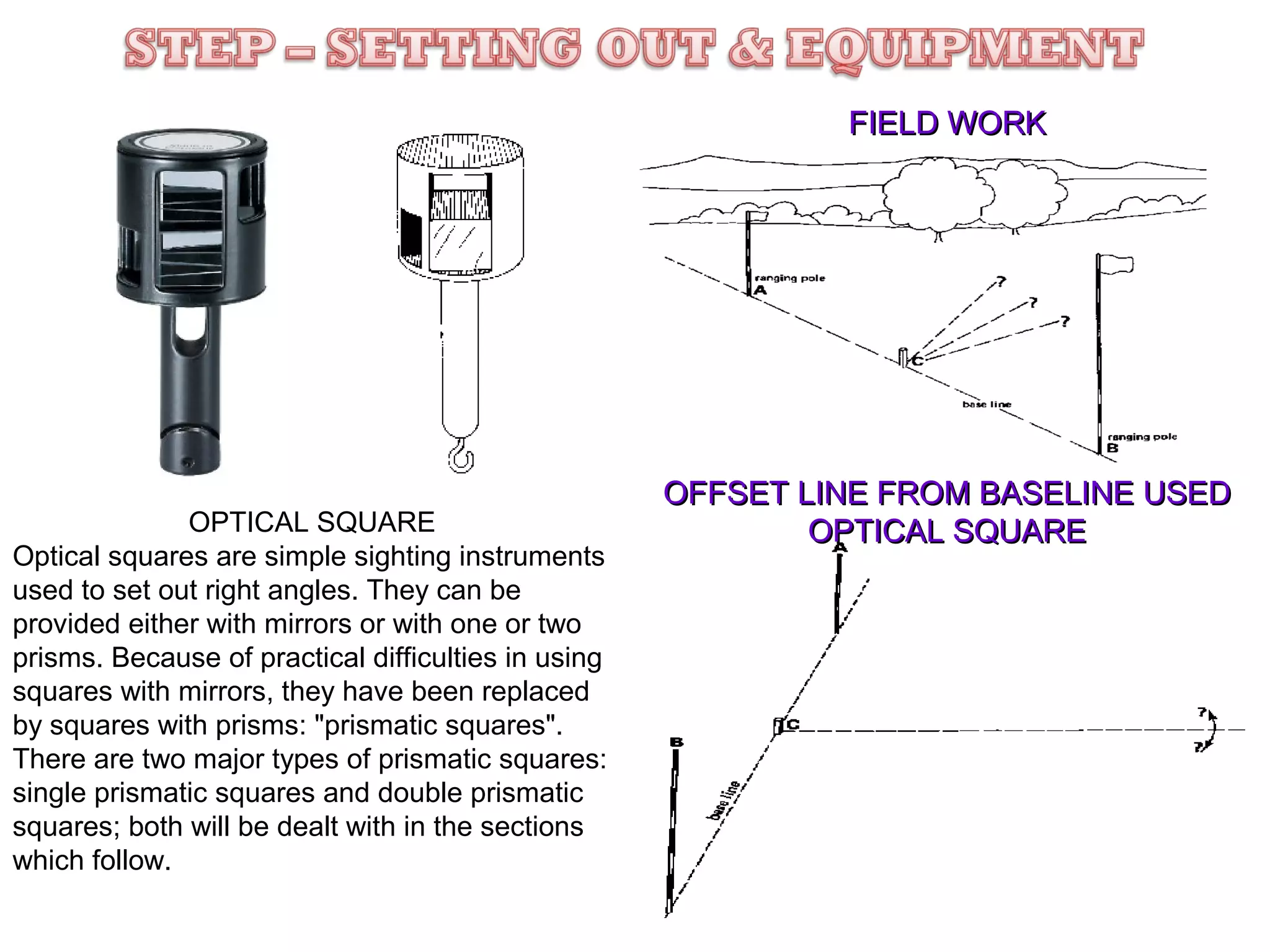
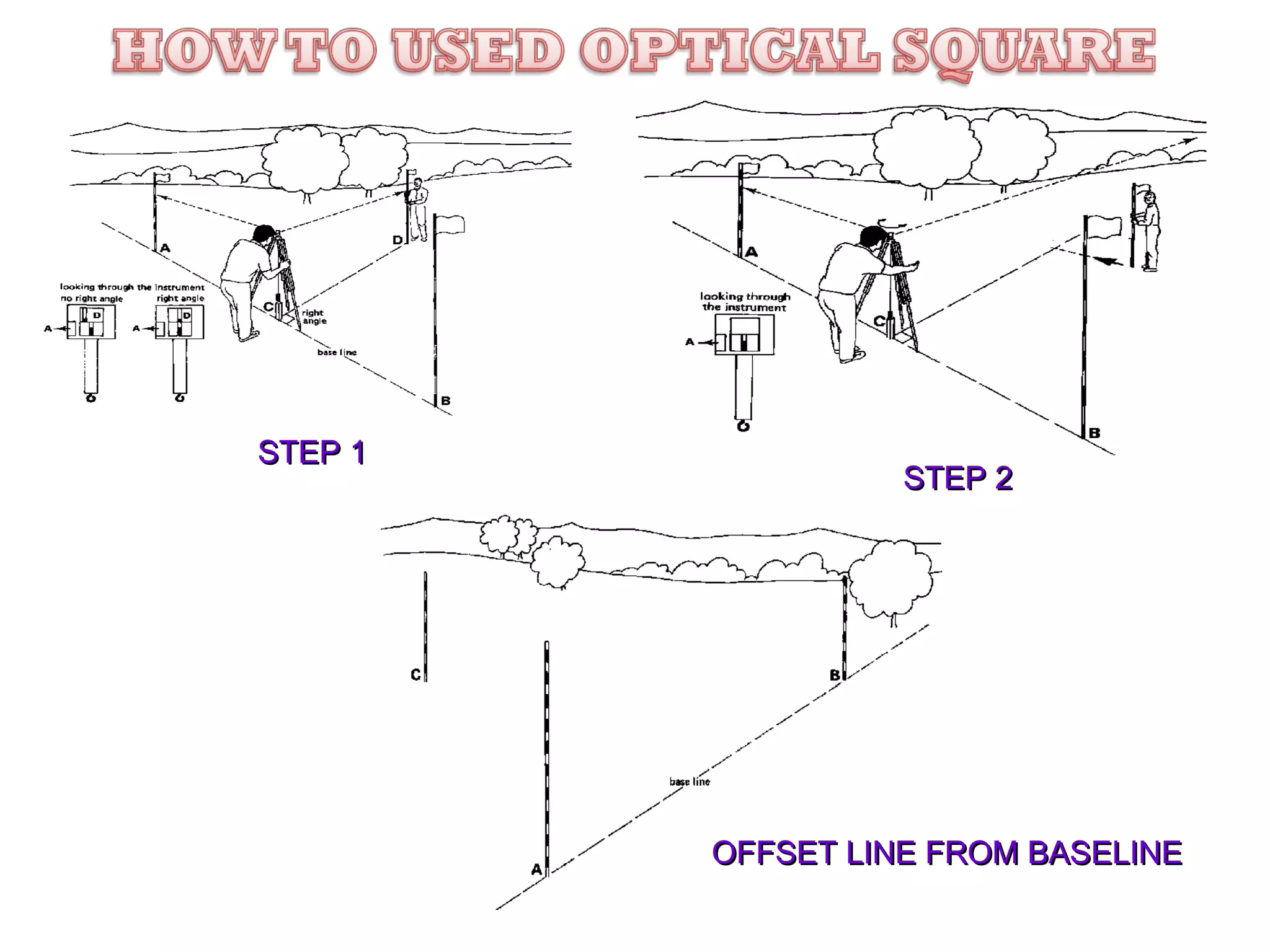
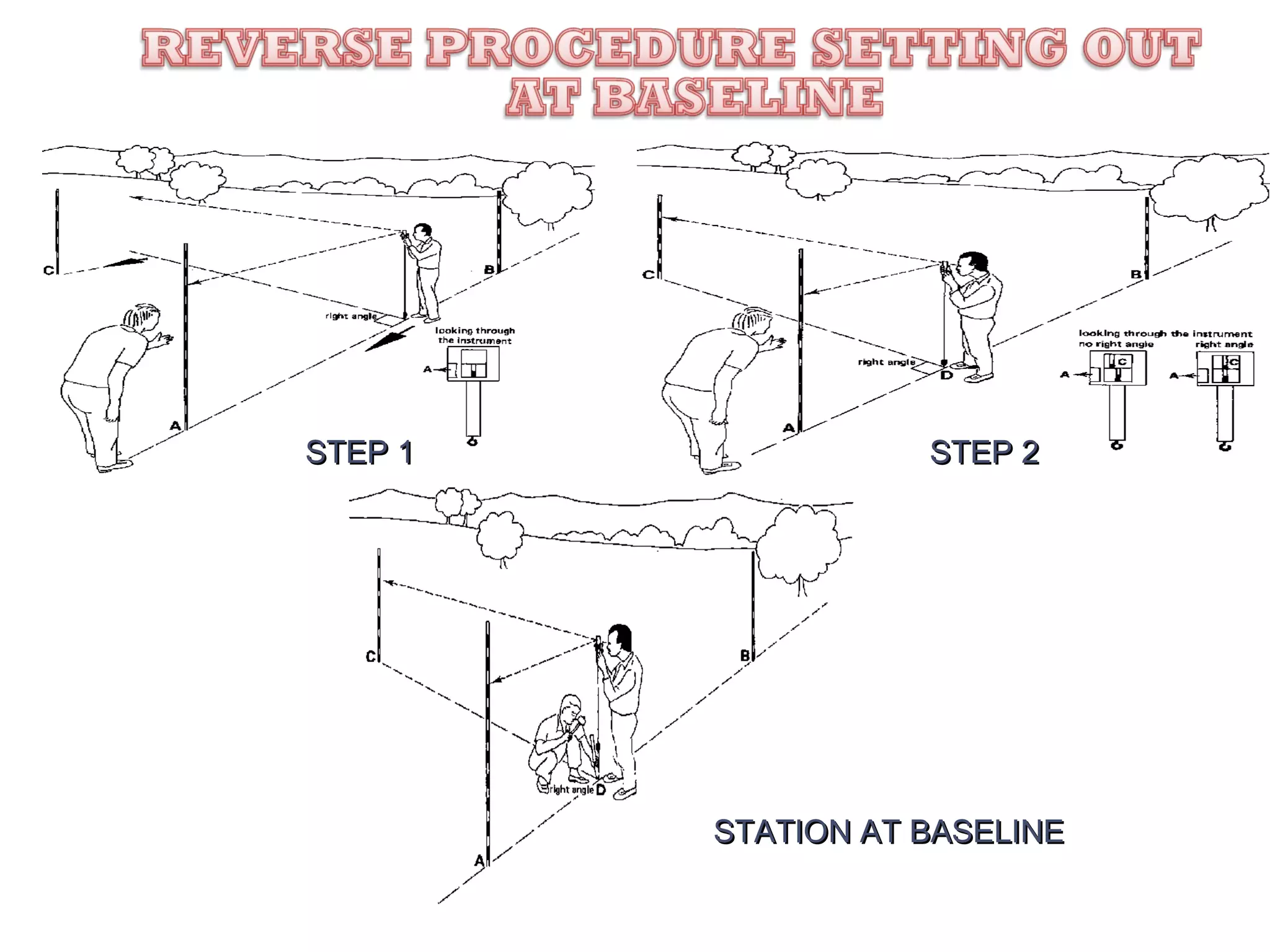
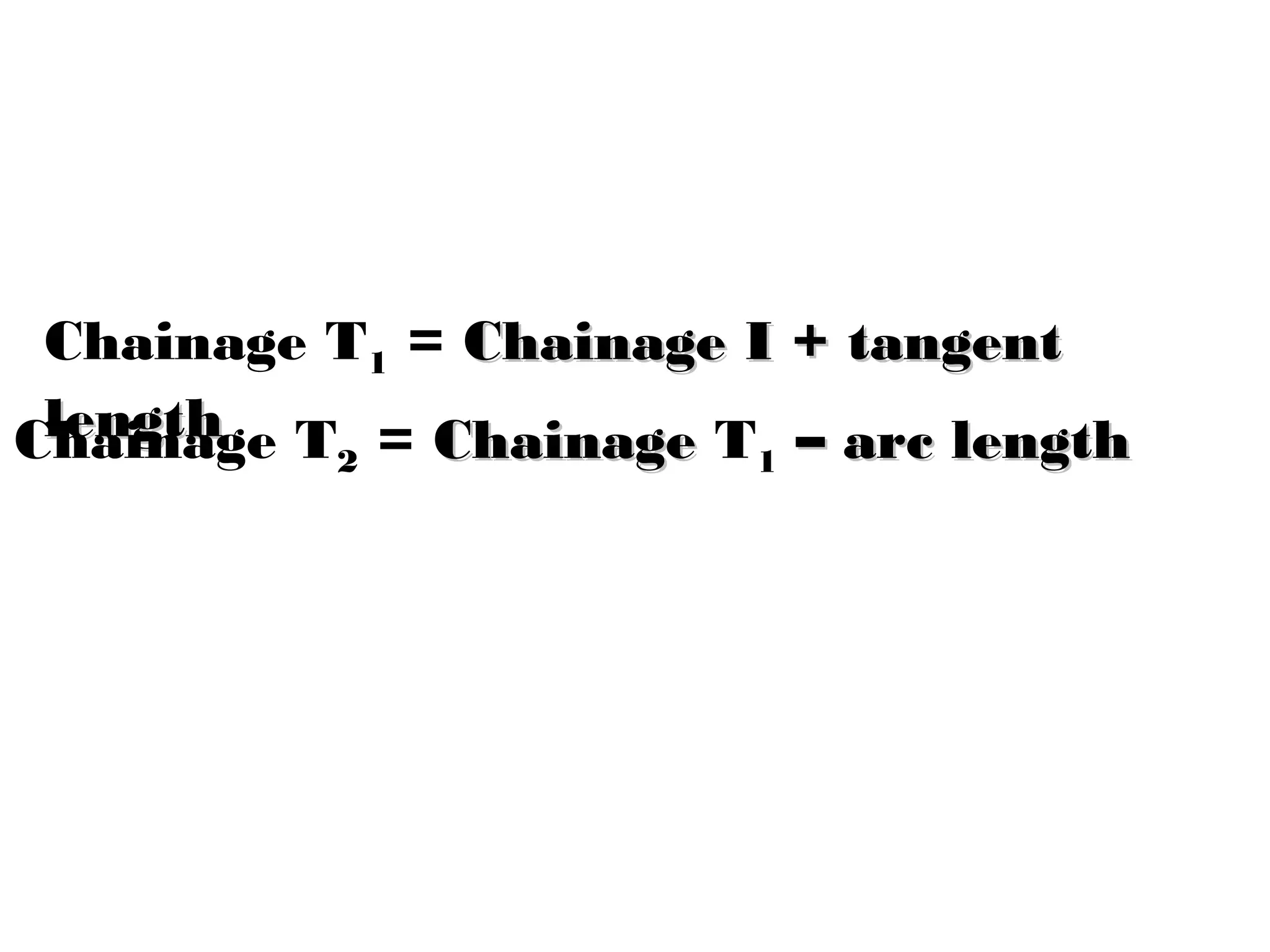Circular curves are used to connect two straight sections of roads, railways, or other infrastructure. There are several common methods for setting out circular curves in the field, including using offsets from the tangent line, offsets from the long chord line, or using deflection angles. Field work involves using tools like optical squares and tapes to accurately mark the curve based on the chosen setting out method. Practical exercises and field work provide opportunities to apply these techniques hands-on.

1. Circular curves

2. Horizontal curves
Definition
Horizontal, circular or simple
curves are curves of constant
radius required to connect
two straights set out on the
ground.
Usage
roads, railways, kerb lines,
pipe lines and may be set out
in several ways, depending on
their length and radius.

3. Circular Curve Geometry

4. FORMULA
θ
T = R tan
2
θ
C = 2 R sin
2
 ∆ 
E = R sec − 1
 2 
θ

M = R1 − cos 
2

θ
L = 2πR
360
δ
1 (deg ree )
1718.9 x C
=
60 R
δ1(min ute ) =
1718.9 x C
R

5. Chainage T1 = Chainage I + tangent
length
Chainage T = Chainage T – arc length
2
1

6. Setting out method
Offset From The Tangent Line
Offset From The Long Chord
Line
Deflection Angle Method
Sub Chords Line Method

7. OFFSET FROM TANGENT LINE
Given
)θ
Radius, R
600m
Deflection
angle , θ
Offset
18 0 24'
Chainage
intersection
point,
formul I
a
IP
Tangent line
Y2
X2
X1
Y1
T1
20m
circular arc
2140
m
X = R − R −Y
2
2
Ofset
T2
Draw the table from the formula:
R R2 Y2 R2-Y2
R −Y
2
2
X = R− R − Y
2
2

8. PROCEDURE
Tangent length
= R tan θ/2
= 600 tan (18°24′/2)
= 97.20m
Chainage T 1
= chainage I – tangent length
= 2140.00 - 97.20
= 2042.80m
Arc length
= 2π x R x θ
360
= 2π x 600 x 18 o 24’
360
Chainage T 2
=
=
= 192.68m
chainage T 1 + arc length
2042.80 + 192.68
= 2235.48m
Ofset
R
R2
Y2
(1)
(2)
(3) = (2)2
(4) = (1)2
R2-Y2
R −Y
2
2
X = R− R − Y
2
2
(5) = (3) – (4)
(6) = √(5)
(7) = (2) – (6)
3600
360000 – 0 =
360000
360000 – 40=
359600
360000 – 1600 =
358400
356400
√ 360000 =
600.000
√ 359600 =
599.667
√ 3584000 =
598.665
596.992
600 – 600 =
0.000
600 – 599.667 =
0.333
600 – 598.665 =
1.335
3.008
80
6400
353600
594.643
5.357
97.20
9447.84
350969.109
592.426
7.574
0
02 = 0
20
202 = 40
40
60
600
6002 =
360000
402 = 1600

9. OFFSET FROM LONG CHORD LINE
Given
Radius, R
600m
Deflection
angle , θ
Offset
18 0 24'
Chainage
intersection
point,
formul I
2140m
20m
a
X = R − Y − R − (W / 2)
2
Ofset
2
R
2
R2
Y2 R2-Y2
Draw the table from the formula:
2
R −Y
2
2
R − (W / 2)
2
2
X = R − Y − R − (W / 2)
2
2
2
2

10. PROCEDURE
Long chord length
= 2R sin θ/2
= 2 x 600 sin (18 °24′/2)
Tangent length
w
= 191.857m
= R tan θ/2
= 600 tan (18°24′/2)
= 97.20m
Chainage T 1
= chainage I – tangent length
= 2140.00 - 97.20
Arc length
= 2π x R x θ
360
= 2π x 600 x 18 o 24’
360
Chainage T 2
=
=
R
R2
Y2
(1)
(2)
(3) = (2) 2
(4) = (1) 2
0
02 = 0
20
202 = 40
40
6002 =
360000
= 2042.80m
= 192.68m
chainage T 1 + arc length
2042.80 + 192.68
Ofse
t
R2-Y2
(5) = (3) – (4)
w/2 = 95.929 m
R −Y
2
= 2235.48m
2
(6) = √(5)
w/2
2
(7)
360000 -0 = √ 360000 =
360000
600.000
360000 – 40 = √ 3596000 =
359600
599.667
95.929 2 =
9202.277
R − (w / 2)
2
2
(8) = √(3) – (7)
x
(9) =(6) – (8)
600 - 692.282
= 7.785
599.667 –
592.282 =
√(360000 –
7.385
6.383
9202.277)=
592.282
4.710
402 = 1600
358400
598.665
3600
356400
596.992
80
6400
353600
594.643
2.361
95.929
9202.277
350797.723
592.282
0.000
60
600

11. DEFLECTION ANGLE
METHOD
Radius, R
600m
Deflection
Given
angle , θ
Offset
18 0 24'
Chainage
intersection
point, I
2140m
20m
Draw the table form for
deflection angle method
formul
a
δ
δ
1 (deg ree )
1 (min ute )
1718.9 x C
=
60 R
1718.9 x C
=
R
Stn
.
Chainag
e
Chord
length
Deflection
angle,δ
(0 ‘ “)
Setting out
angle, δ
(0 ‘ “)

12. Tangent length
= R tan θ/2
= 600 tan (18°24′/2)
PROCEDUR
1718.9 x 17.179
δ =
E60xx600.000
1718.9 20
= 97.20m
Chainage T 1
= chainage I – tangent length
= 2140.00 - 97.20
= 2042.80m
Arc length
= R x θ x 2π
360
= 600 x 18 o 24’ x 2π
360
Chainage T 2
Stn.
=
=
Chainage
δ =
chainage T 1 + arc length
2042.80 + 192.68
=
Chord length, C
60 x600
1718.9 x 15.506
δ =
2235.48m
60 x600
= 192.684m
Setting out angle, δ
(0 ‘ “) – cumulative deflection
Deflection angle,δ
(0 ‘ “) – use formula
+
+
angle
=
=
T1
2042.821
0
00 0’ 0”
00 0’ 0”
δ1
2060
17.179
00 49’ 12”
δ2
2080
20.000
00 57’ 18”
10 46’ 30”
δ3
2100
20.000
00 57’ 18”
20 43’ 48”
δ4
2120
20.000
00 57’ 18”
30 41’ 6”
δ5
2140
20.000
00 57’ 18”
40 38’ 24”
δ6
2160
20.000
00 57’ 18”
50 35’ 42”
δ7
2180
20.000
00 57’ 18”
60 33’ 0”
δ8
2200
20.000
00 57’ 18”
70 30’ 18”
δ9
2220
20.000
00 57’ 18”
80 27’ 36”
T2
2235.506
15.506
00 44’ 25”
90 12’ 1”
Σ = 192.684
Σ = 90 12’ 1”
00 49’ 12”
θ / 2 = 180 24’ / 2 = 90 12’ 1”

13. Sub chords line method
Radius, R
600m
Deflection
angle , θ
Offset
18 0 24'
Chainage
intersection
formul
point, I
2140m
• Given
a
a
Ofset =
2R
b(b + a)
Ofset =
2R
b
Ofset =
R
2
1
2
2
n
Ofset =
n −1
c (c + b)
2R
20m
Draw the table form for
sub chord line method
Stn
.
Chainag
e
Chord
length
Offset

14. Tangent length
Chainage T 1
Arc length
Chainage T 2
= R tan θ/2
= 600 tan (18°24′/2)
PROCEDUR
17.179
Ofset =
2x
E600
= 97.20m
2
= chainage I – tangent length
1
= 2140.00 - 97.20
= 2042.80m
20(20 + 17.179)
Ofset
= 192.684m =
2 x600
20
= chainage T
+ arc length
Ofset
= 2042.80 + 192.68
= 2235.48m =
600
15.506(15.506 + 20)
Chord
Offset
Ofset =
length
2 x600
0
= R x θ x 2π
360
= 600 x 18 o 24’ x 2π
360
2
2
1
n
Stn
.
T1
δ1
δ2
δ3
δ4
δ5
δ6
δ7
δ8
δ9
T2
Chainag
e
2042.821
2060
2080
2100
2120
2140
2160
2180
2200
2220
2235.506
n −1
a = 17.179
b = 20.000
20.000
20.000
20.000
20.000
20.000
20.000
20.000
c =15.506
Σ = 192.684
0.246
0.620
0.667
0.667
0.667
0.667
0.667
0.667
0.667
0.459
-
First Offset
Second Offset
Other Offset
Last Offset

15. PROCEDURE ways, depending on the accuracy
SETTING
Circular curves may be set out in a variety of
required, its radius of curvature and obstructions on site.
OUT
Methods of setting out are as follows:
•Using one theodolite and a tape by the tangent angle method. This method
can be used on all curves, but is necessary for long curves of radius unless
they are set out by coordinates.
•Using two theodolites. This method can be used on smaller curves where the
whole length is visible from both tangent points and where two instruments are
available.
•Using tapes only by the method of offsets from the tangent. This method is
used for minor curves only.
•Using tapes only by the method of offsets from the long chord. This method is
used for short radius curves.

16. FIELD WORK
OPTICAL SQUARE
Optical squares are simple sighting instruments
used to set out right angles. They can be
provided either with mirrors or with one or two
prisms. Because of practical difficulties in using
squares with mirrors, they have been replaced
by squares with prisms: "prismatic squares".
There are two major types of prismatic squares:
single prismatic squares and double prismatic
squares; both will be dealt with in the sections
which follow.
OFFSET LINE FROM BASELINE USED
OPTICAL SQUARE

17. STEP 1
STEP 2
OFFSET LINE FROM BASELINE

18. STEP 1
STEP 2
STATION AT BASELINE

19. End of sub -topic
• Exercise
• Practical 6 & 7