Downloaded 69 times
Uploaded bykmasz kamal
Tachymetry lesson 5 tangent system
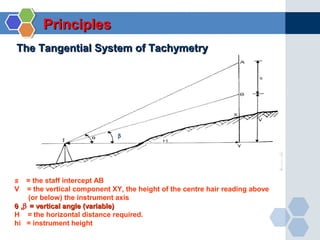
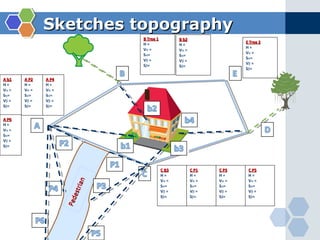
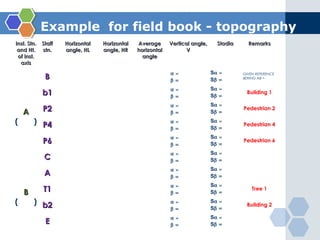
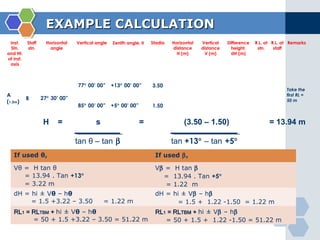
This document provides instruction on using the tangential tachymetry system to calculate horizontal distances, vertical distances, and reduced levels between stations. It includes the key formulas and principles, such as using the staff intercept (s) and vertical angles (θ and β) to calculate the horizontal distance (H). It also provides examples of field book layout and calculations. The goal is to use vertical angles and stadia readings to determine horizontal distances, vertical distances, and reduced levels between stations to map topographical features and surfaces.
More Related Content
Similar to Tachymetry lesson 5 tangent system
Tachymetry lesson 5 tangent system
- 1.
- 2.
- 3. Principles The Tangential Systemof Tachymetry β s V = the staff intercept AB = the vertical component XY, the height of the centre hair reading above (or below) the instrument axis θ ,β = vertical angle (variable) H = the horizontal distance required. hi = instrument height
- 4. Publication formula AY = Htan θ BY = H tan β AY –BY = s = H ( tan θ – tan β) H = s tan θ – tan β Horizontal distance If used θ, If used β, Vertical distance Vθ = H tan θ Vβ = H tan β Difference height dH = hi ± Vθ – hθ dH = hi ± Vβ – hβ Reduced level RL1 = RLTBM + hi ± Vθ – hθ RL1 = RLTBM + hi ± Vβ – hβ
- 5. Where S = staffintercept H = horizontal distance V = vertical distance θ = zenith angle (θ > β) hi = the height of instrument (always positive) h = the centre hair reading (θ @ β) RL= Reduced level RL
- 6. Work procedure EXAMPLE RESULTPRACTICAL 3 - TACHEOMETRY BOOKING FORM (The Tangential System ) Inst. Stn. Staff and Ht. of stn inst. axis Horizontal angle, HL Horizontal angle, HR SETTING SETTING A B 105015’30” 285015’30” (1.455 m) C 155010’36” 335012’30” C A 335 11’33” 155011’33” (1.305 m) D 45020’26” SETTING SETTING 0 225032’30” Average horizontal angle Vertical angle, V α =95011’25” β = 92010’20” α =90012’20” 335011’33” β = 90010’10” α =83020’25” β = 85016’25” α =88018’10” 225026’28” β = 89028’00” Stadia hα =1.205 hβ =1.525 hα =1.050 hβ =1.450 hα =1.345 hβ =1.205 hα =1.250 hβ =1.205 Remarks GIVEN REFERENCE BERING AB = 105015’30”
- 7. Practical 3 • GIVENTHE TBM (Temporary bench mark) – Stn A & B • DETERMINING THE NUMBER OF STATIONS • READING VERTICAL ANGLE BELONG THE SITUATION • TRAVERSE METHOD • TAKE TOPOGRAPHY ITEMS (Tree, Building, Pedestrian)
- 8. Sketches topography B Tree1 H= Vα = Sα= Vβ = Sβ= A b1 H= Vα = Sα= Vβ = Sβ= A P2 H= Vα = Sα= Vβ = Sβ= B b2 H= Vα = Sα= Vβ = Sβ= E Tree 2 H= Vα = Sα= Vβ = Sβ= A P4 H= Vα = Sα= Vβ = Sβ= Ped e str ia n A P6 H= Vα = Sα= Vβ = Sβ= C B3 H= Vα = Sα= Vβ = Sβ= C P1 H= Vα = Sα= Vβ = Sβ= C P3 H= Vα = Sα= Vβ = Sβ= C P5 H= Vα = Sα= Vβ = Sβ=
- 9. Example for fieldbook - topography Inst. Stn. and Ht. of inst. axis Staff stn. Horizontal angle, HL Horizontal angle, HR Average horizontal angle Vertical angle, V Stadia Remarks B α = β = Sα = Sβ = GIVEN REFERENCE BERING AB = b1 α = β = Sα = Sβ = Building 1 P2 α = β = Sα = Sβ = Pedestrian 2 α = β = Sα = Sβ = Pedestrian 4 P6 α = β = Sα = Sβ = Pedestrian 6 C α = β = Sα = Sβ = A α = β = Sα = Sβ = T1 α = β = Sα = Sβ = Tree 1 α = β = Sα = Sβ = Building 2 α = β = Sα = Sβ = A (155 ) P4 B (155 ) b2 E
- 10. EXAMPLE CALCULATION Inst. Stn. and Ht. ofinst. axis Staff stn. Horizontal angle Vertical angle Zenith angle, θ Stadia 77° 00’ 00” A (1.5m) B +13° 00’ 00” +5° 00’ 00” Vertical distance V (m) Difference height, dH (m) R.L. at R.L. at Remarks stn. staff 3.50 85° 00’ 00” Horizontal distance H (m) 1.50 Take the first RL = 50 m 27° 30’ 00” H = s = tan θ – tan β (3.50 – 1.50) = 13.94 m tan +13° – tan +5° If used θ, If used β, Vθ = H tan θ = 13.94 . Tan +13° = 3.22 m Vβ = = = dH = dH = hi ± Vθ – hθ = 1.5 +3.22 – 3.50 = 1.22 m RL1 = RLTBM + hi ± Vθ – hθ = 50 + 1.5 +3.22 – 3.50 = 51.22 m H tan β 13.94 . Tan +5° 1.22 m hi ± Vβ – hβ = 1.5 + 1.22 -1.50 = 1.22 m RL1 = RLTBM + hi ± Vβ – hβ = 50 + 1.5 + 1.22 -1.50 = 51.22 m
- 11.