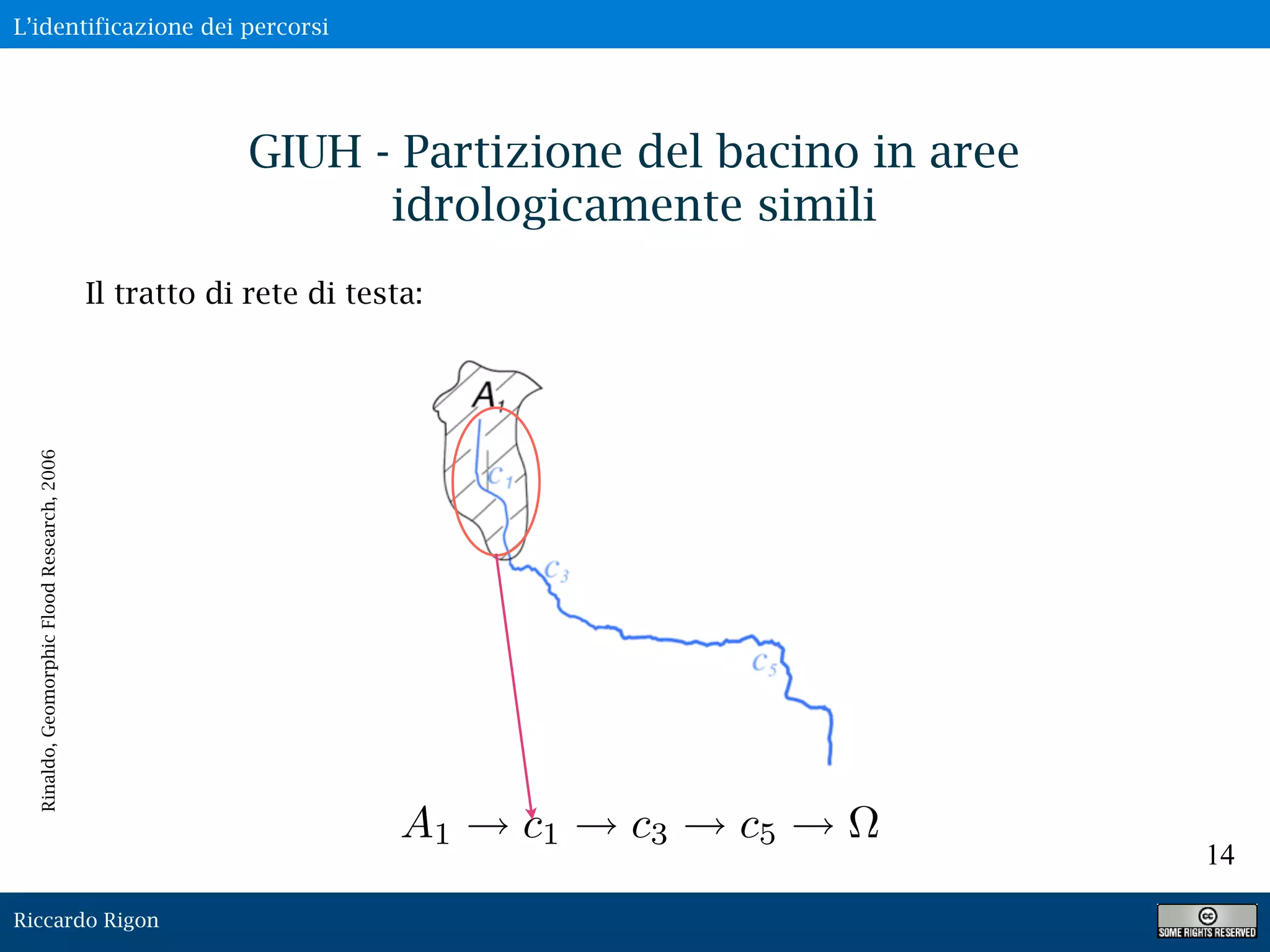
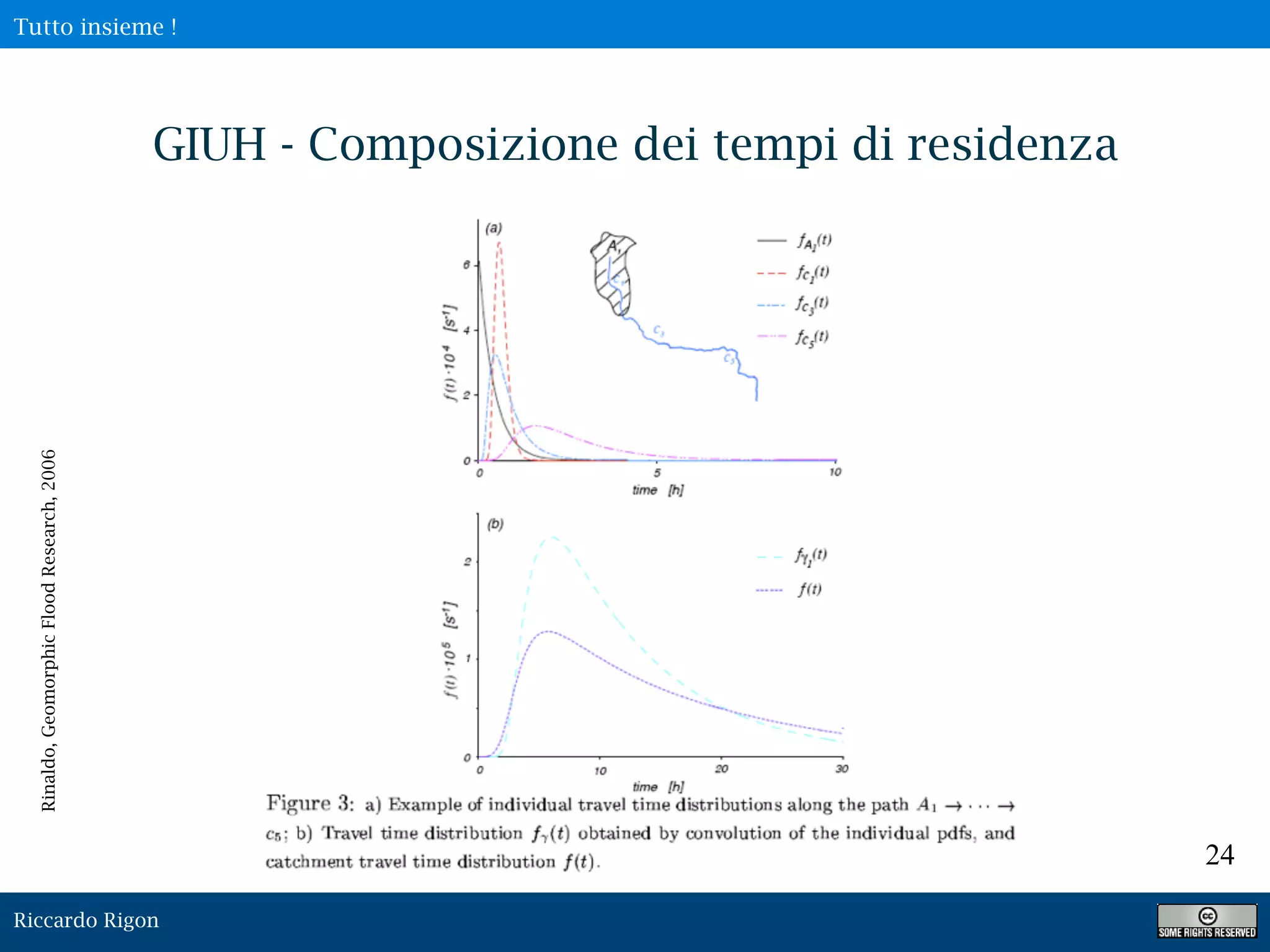
Il documento presenta il concetto di idrogramma istantaneo unitario geomorfologico (GIUH), evidenziando l'importanza della partizione del bacino in unità idrologicamente simili e l'analisi delle distribuzioni dei tempi di residenza. Vengono discussi metodi per la determinazione delle forme funzionali delle distribuzioni e l'impatto delle incertezze statistiche nella previsione del deflusso. Infine, viene presentata una formula generale per calcolare il GIUH e i parametri necessari per la calibrazione del modello idrologico.