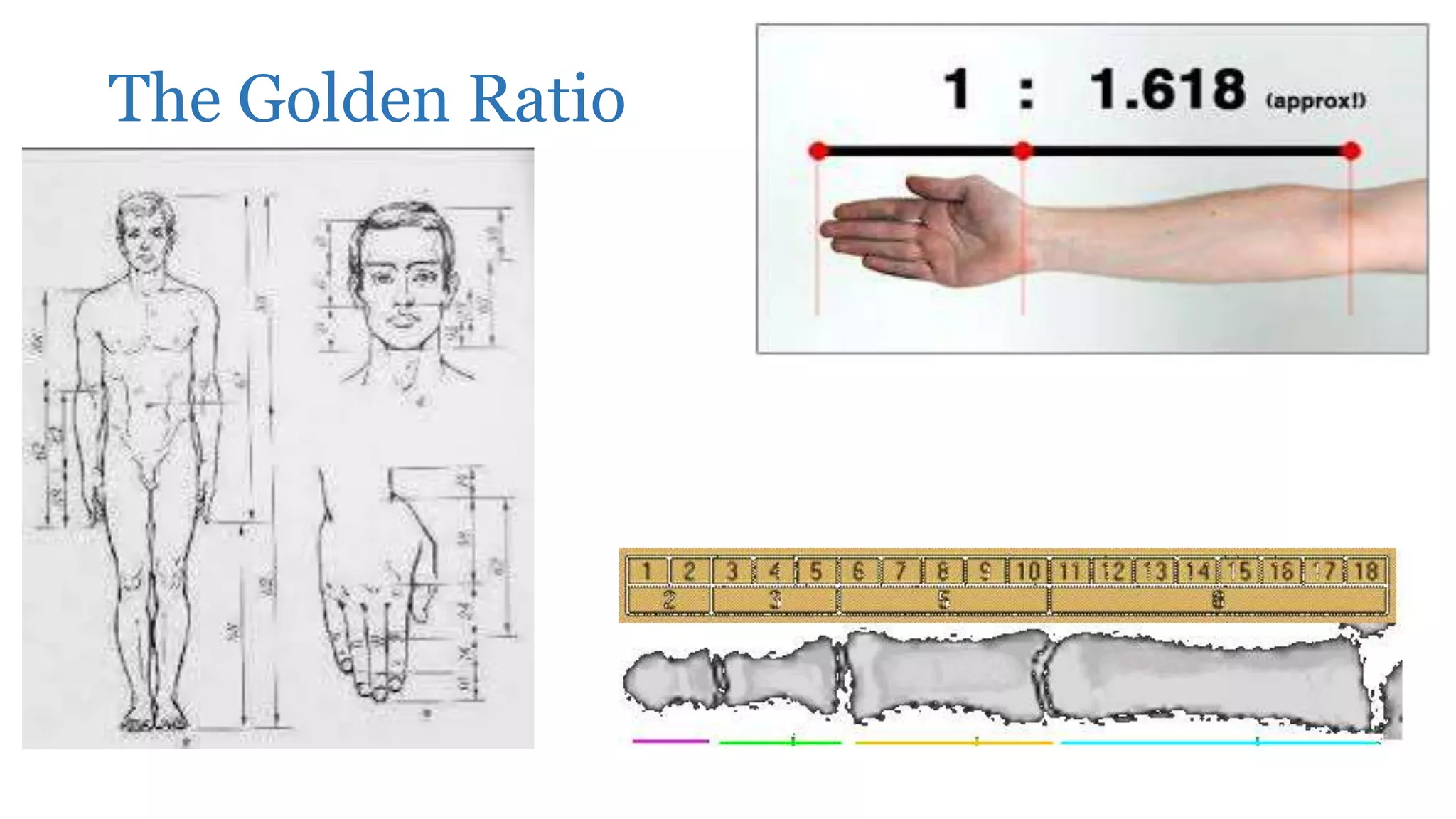
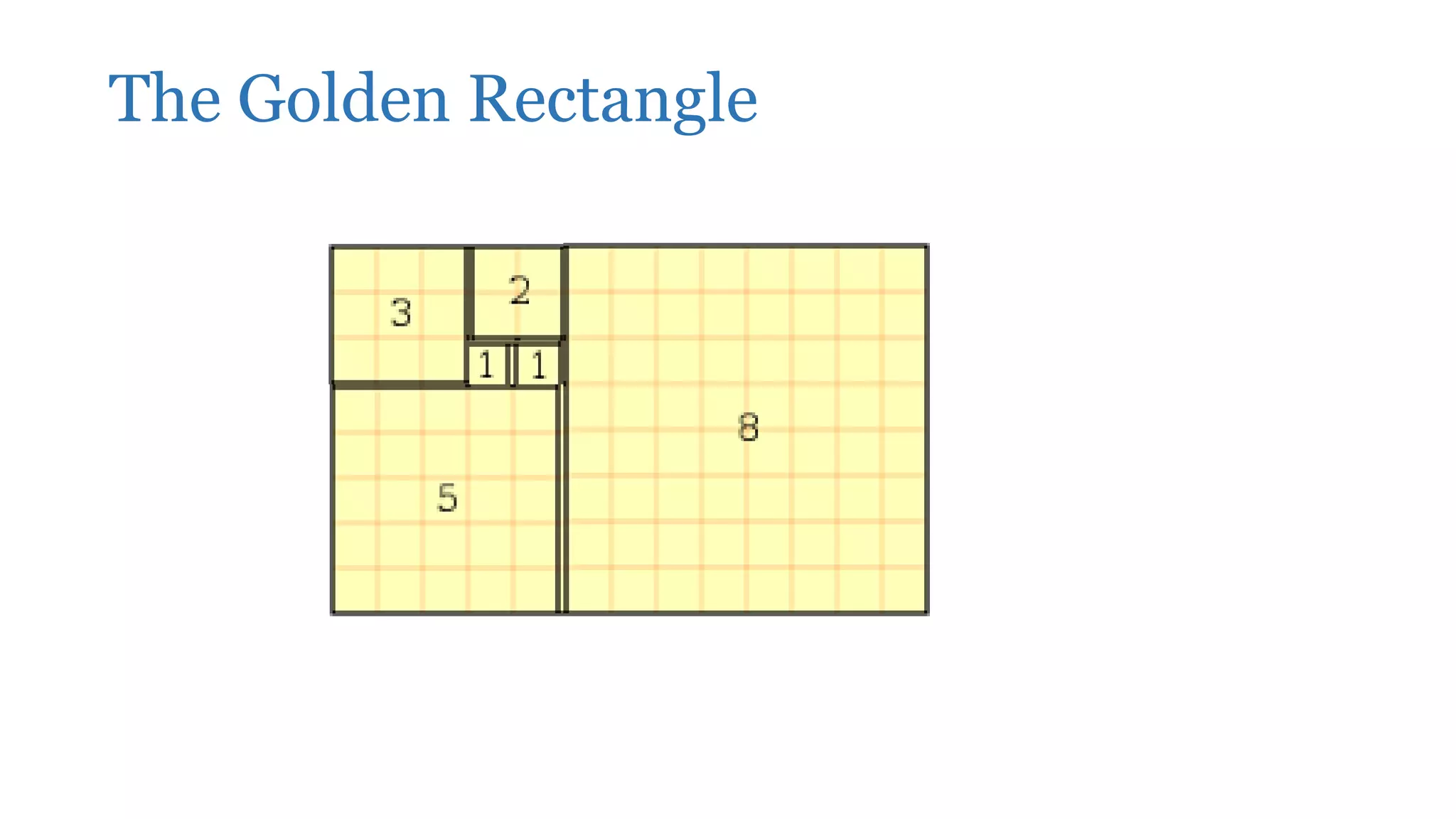
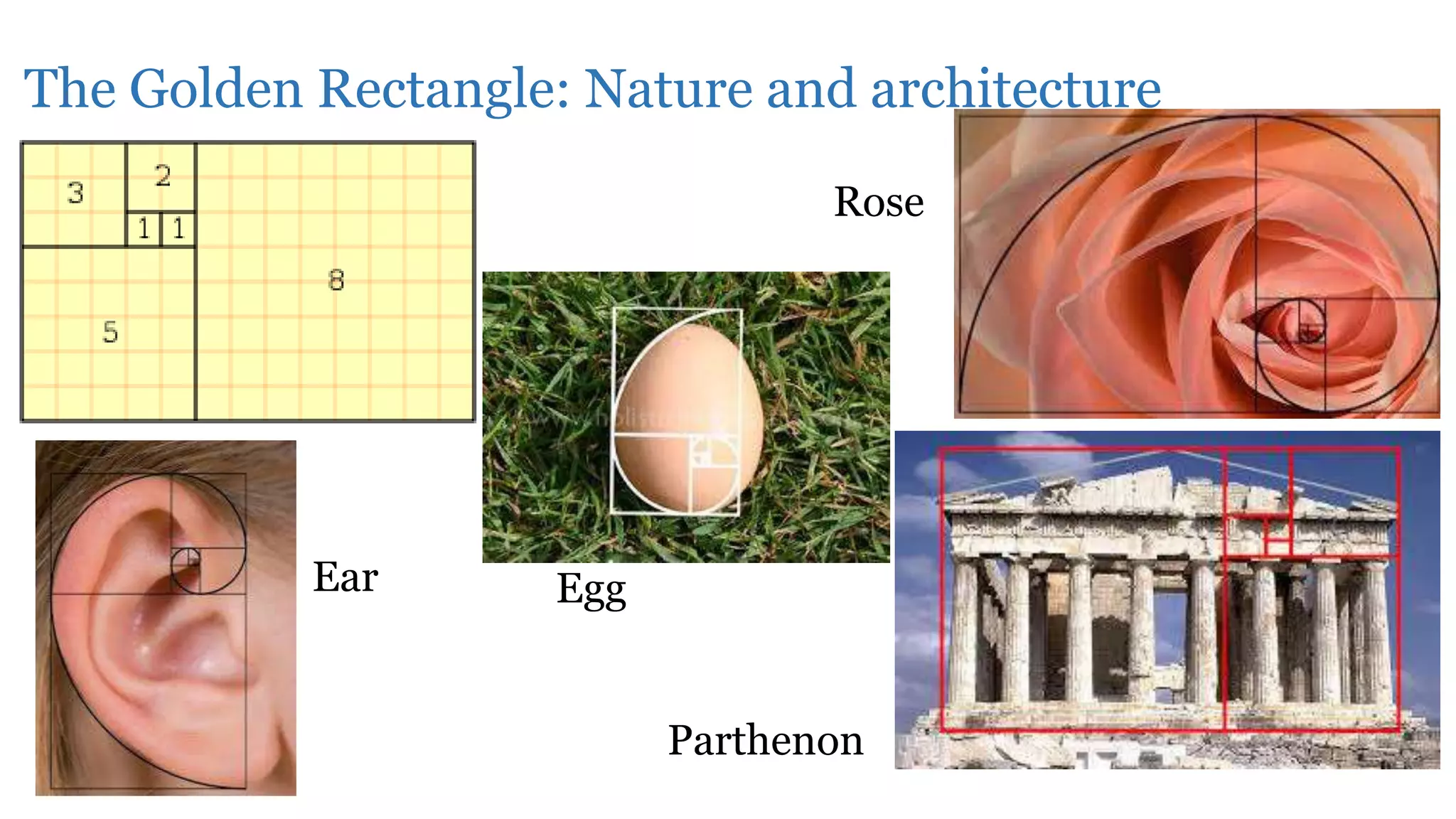
The Fibonacci sequence is a sequence where each number is the sum of the two preceding numbers. This sequence appears frequently in nature, such as the spiral patterns of shells, flowers, pine cones, and galaxies. The golden ratio is the number approximately equal to 1.6180 that results from dividing any number in the Fibonacci sequence by its predecessor. Both the Fibonacci sequence and golden ratio are found in architecture, like the Parthenon, as well as in music scales.

1. The Fibonacci Sequence
and the Golden Ratio

2. Leonardo da Pisa – Fibonacci
Fibonacci is the greatest European
mathematician of the middle ages
Born in 1170 and died in 1240
He introduced the Arabic number
system in Europe

3. Fibonacci Sequence
The sequence in which each number is the SUM of the two
preceding numbers
+ + + + + + + +++
1 2 3 5 8 13 21 34 55 89 2331441
+

4. The Fibonacci sequence in nature:
Flowers
1 Petal 5 Petals3 Petals
8 Petals 13 Petals

5. The Fibonacci sequence in nature: Spirals
Nautilus Shell
Cauliflower
Pine Conehttps://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html
Why do we find the Fibonacci sequence in
nature?
Does nature study mathematics?
Hurricane
Galaxy

6. The Golden Ratio
: : ::
55 89 144 233 377
Every number of the Fibonacci sequence divided for the preceding one
is always:
1.61801.61801.61801.6180

7. The Golden Ratio

8. The Golden Rectangle

9. The Golden Rectangle: Nature and architecture
Ear Egg
Rose
Parthenon

10. The Fibonacci Sequence: Music
In an octave there are 13 keys: 8 are white and 5 are black

11. To sum up
The Fibonacci sequence:
A sequence in which every number is the SUM of the preceding
two
The Golden Rectangle:
A rectangle built according to the Fibonacci sequence
The Golden Ratio:
The number you get DIVIDING a number of the Fibonacci sequence for
the preceding one:
1.6180