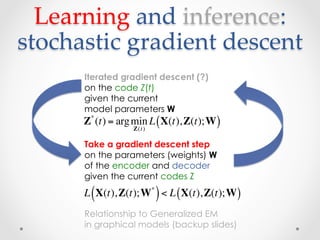
The document provides an introduction and overview of auto-encoders, including their architecture, learning and inference processes, and applications. It discusses how auto-encoders can learn hierarchical representations of data in an unsupervised manner by compressing the input into a code and then reconstructing the output from that code. Sparse auto-encoders and stacking multiple auto-encoders are also covered. The document uses handwritten digit recognition as an example application to illustrate these concepts.

1. INTRODUCTION TO
AUTO-ENCODERS
YAN XU
HOUSTON MACHINE LEARNING
09-29-2018

2. Calling for abstracts

3. Review of
auto-­‐‑encoders
Piotr Mirowski, Microsoft Bing London
Deep Learning Meetup
March 26, 2014
Code
Input
Code prediction
Code energy
Decoding energy
Input decoding
Sparsity
constraint
X
Z

4. Outline
• Deep learning concepts covered
o Hierarchical representations
o Sparse and/or distributed representations
o Supervised vs. unsupervised learning
• Auto-encoder
o Architecture
o Inference and learning
o Sparse coding
o Sparse auto-encoders
• Illustration: handwritten digits
o Stacking auto-encoders
o Learning representations of digits
o Impact on classification
• Applications to text
o Semantic hashing
o Semi-supervised learning
o Moving away from auto-encoders
• Topics not covered in this talk
Walk through codes of "Building Autoencoders in Keras".
dddddddddddddddddddddddddddddddddddd

5. Outline
• Deep learning concepts covered
o Hierarchical representations
o Sparse and/or distributed representations
o Supervised vs. unsupervised learning
• Auto-encoder
o Architecture
o Inference and learning
o Sparse coding
o Sparse auto-encoders
• Illustration: handwritten digits
o Stacking auto-encoders
o Learning representations of digits
o Impact on classification
• Applications to text
o Semantic hashing
o Semi-supervised learning
o Moving away from auto-encoders
• Topics not covered in this talk

6. Hierarchical
representations
“Deep learning methods aim at
learning feature hierarchies
with features from higher levels
of the hierarchy formed by the
composition of lower level
features.
Automatically learning features
at multiple levels of abstraction
allows a system
to learn complex functions
mapping the input to the output
directly from data,
without depending completely
on human-crafted features.”
— Yoshua Bengio
[Bengio, “On the expressive power of deep architectures”, Talk at ALT, 2011]
[Bengio, Learning Deep Architectures for AI, 2009]

7. Sparse and/or distributed
representations
Example on MNIST handwritten digits
An image of size 28x28 pixels can be represented
using a small combination of codes from a basis set.
+ 1 + 1= 1 + 1 + 1 + 1 + 1 + 0.8 + 0.8
Figure 4: Top: A randomly selected subset of encoder filters learned by our energy-based model
when trained on the MNIST handwritten digit dataset. Bottom: An example of reconstruction of a
digit randomly extracted from the test data set. The reconstruction is made by adding “parts”: it is
the additive linear combination of few basis functions of the decoder with positive coefficients.
Examples of learned encoder and decoder filters are shown in figure 3. They are spatially localized,
and have different orientations, frequencies and scales. They are somewhat similar to, but more
localized than, Gabor wavelets and are reminiscent of the receptive fields of V1 neurons. Interest-
ingly, the encoder and decoder filter values are nearly identical up to a scale factor. After training,
inference is extremely fast, requiring only a simple matrix-vector multiplication.
[Ranzato, Poultney, Chopra & LeCun, “Efficient Learning of Sparse Representations with an Energy-­‐‑Based Model ”, NIPS, 2006;
Ranzato, Boureau & LeCun, “Sparse Feature Learning for Deep Belief Networks ”, NIPS, 2007]
Biological motivation: V1 visual cortex

8. Sparse and/or distributed
representations
Example on MNIST handwritten digits
An image of size 28x28 pixels can be represented
using a small combination of codes from a basis set.
+ 1 + 1= 1 + 1 + 1 + 1 + 1 + 0.8 + 0.8
Figure 4: Top: A randomly selected subset of encoder filters learned by our energy-based model
when trained on the MNIST handwritten digit dataset. Bottom: An example of reconstruction of a
digit randomly extracted from the test data set. The reconstruction is made by adding “parts”: it is
the additive linear combination of few basis functions of the decoder with positive coefficients.
Examples of learned encoder and decoder filters are shown in figure 3. They are spatially localized,
and have different orientations, frequencies and scales. They are somewhat similar to, but more
localized than, Gabor wavelets and are reminiscent of the receptive fields of V1 neurons. Interest-
ingly, the encoder and decoder filter values are nearly identical up to a scale factor. After training,
inference is extremely fast, requiring only a simple matrix-vector multiplication.
At the end of this talk, you should know how to learn that basis set
and how to infer the codes, in a 2-layer auto-encoder architecture.
Matlab/Octave code and the MNIST dataset will be provided.
[Ranzato, Poultney, Chopra & LeCun, “Efficient Learning of Sparse Representations with an Energy-­‐‑Based Model ”, NIPS, 2006;
Ranzato, Boureau & LeCun, “Sparse Feature Learning for Deep Belief Networks ”, NIPS, 2007]
Biological motivation: V1 visual cortex (backup slides)

9. Supervised learning
X
Y
Ef Y, ˆY( )
Target
Input
Prediction
Error
ˆY = f X;W,b( )

10. Supervised learning
Y − ˆY
2
2
Target
Input
Prediction
Error
ˆY = WT
X + b
X
Y

11. Why not exploit
unlabeled data?

12. Unsupervised learning
No target…
Input
Prediction
No error…
ˆY = f X;W,b( )
X
?

13. Unsupervised learning
Code
“latent/hidden”
representation
Input
Prediction(s)
Error(s)
X
Z

14. Unsupervised learning
Code
Input
Prediction(s)
Error(s)
We want
the codes
to represent
the inputs
in the dataset.
The code should
be a compact
representation
of the inputs:
low-dimensional
and/or sparse.
X
Z

15. Examples of
unsupervised learning
• Linear decomposition of the inputs:
o Principal Component Analysis and Singular Value Decomposition
o Independent Component Analysis [Bell & Sejnowski, 1995]
o Sparse coding [Olshausen & Field, 1997]
o …
• Fitting a distribution to the inputs:
o Mixtures of Gaussians
o Use of Expectation-Maximization algorithm [Dempster et al, 1977]
o …
• For text or discrete data:
o Latent Semantic Indexing [Deerwester et al, 1990]
o Probabilistic Latent Semantic Indexing [Hofmann et al, 1999]
o Latent Dirichlet Allocation [Blei et al, 2003]
o Semantic Hashing
o …

16. Objective of this tutorial
Study a fundamental building block
for deep learning,
the auto-encoder

17. Outline
• Deep learning concepts covered
o Hierarchical representations
o Sparse and/or distributed representations
o Supervised vs. unsupervised learning
• Auto-encoder
o Architecture
o Inference and learning
o Sparse coding
o Sparse auto-encoders
• Illustration: handwritten digits
o Stacking auto-encoders
o Learning representations of digits
o Impact on classification
• Applications to text
o Semantic hashing
o Semi-supervised learning
o Moving away from auto-encoders
• Topics not covered in this talk

18. Auto-­‐‑encoder
Code
Input X
Z
Target
= input
Y = X
Code
Input
“Bottleneck” code
i.e., low-dimensional,
typically dense,
distributed
representation
“Overcomplete” code
i.e., high-dimensional,
always sparse,
distributed
representation
Target
= input

19. Auto-­‐‑encoder
Eg Z, ˆZ( )
Code
Input
Code
prediction
Encoding
“energy”
ˆZ = g X;C,bC( ) Eh X, ˆX( )
ˆX = h Z;D,bD( )
Decoding
“energy”
Input
decoding
X
Z

20. Auto-­‐‑encoder
Z − ˆZ
2
2
Code
Input
Code
prediction
Encoding
energy
X − ˆX
2
2 Decoding
energy
Input
decoding
X
Z
ˆZ = g X;C,bC( )
ˆX = h Z;D,bD( )

21. Auto-­‐‑encoder
loss function
L X(t), Z(t);W( )=α Z(t)− g X(t);C,bC( ) 2
2
+ X(t)− h Z(t);D,bD( ) 2
2
L X,Z;W( )= α Z(t)− g X(t);C,bC( ) 2
2
t=1
T
∑ + X(t)− h Z(t);D,bD( ) 2
2
t=1
T
∑
Encoding energy Decoding energy
Encoding energy Decoding energy
For one sample t
For all T samples
How do we get the codes Z?
coefficient of
the encoder error
We note W={C, bC, D, bD}

22. Learning and inference in
auto-­‐‑encoders
Z* = argmin
Z
L X,Z;W( )
W* = argmin
W
L X,Z;W( )
Learn the parameters (weights) W
of the encoder and decoder
given the current codes Z
Infer the codes Z
given the current
model parameters W
Relationship to Expectation-Maximization
in graphical models (backup slides)

23. Learning and inference:
stochastic gradient descent
Z*
(t) = argmin
Z(t)
L X(t),Z(t);W( )
L X(t),Z(t);W*
( )< L X(t),Z(t);W( )
Take a gradient descent step
on the parameters (weights) W
of the encoder and decoder
given the current codes Z
Iterated gradient descent (?)
on the code Z(t)
given the current
model parameters W
Relationship to Generalized EM
in graphical models (backup slides)

24. Auto-­‐‑encoder
Z − ˆZ
2
2
Code
Input
Code
prediction
Encoding
energy
ˆZ = CT
X + bC
X − ˆX
2
2
A =σ Z( )=
1
1+e−Z
ˆX = DT
A+ bD
Decoding
energy
Input
decoding
X
Z

25. Under-complete auto-encoders

26. Under-complete auto-encoders

27. Sparse auto-encoders

28. Denoising Auto-encoders

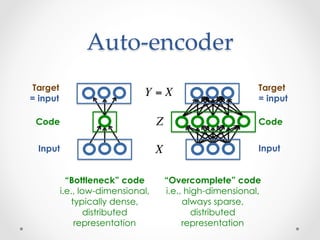
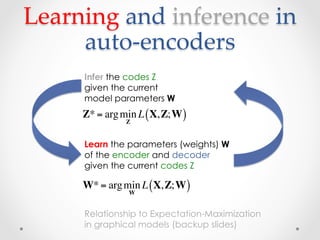
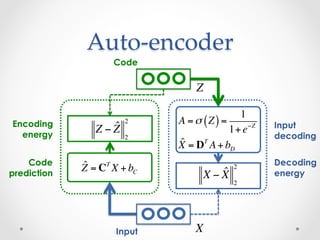
29. Stacking auto-­‐‑encoders
Code
Input
Code prediction
Code energy
Decoding energy
Input decoding
Sparsity
constraint
X
Z
Code
Input
Code prediction
Code energy
Decoding energy
Input decoding
Sparsity
constraint
X
Z
[Ranzato, Boureau & LeCun, “Sparse Feature Learning for Deep Belief Networks ”, NIPS, 2007]
Video:
Autoencoder applications:
https://www.youtube.com/watch?
v=J4DsymeZe2g

30. MNIST handwricen digits
• Database of 70k
handwritten digits
o Training set: 60k
o Test set: 10k
• 28 x 28 pixels
• Best performing
classifiers:
o Linear classifier: 12% error
o Gaussian SVM 1.4% error
o ConvNets <1% error
[hcp://yann.lecun.com/exdb/mnist/]
https://blog.keras.io/building-autoenc
oders-in-keras.html

31. Stacked auto-­‐‑encoders
Code
Input
Code prediction
Code energy
Decoding energy
Input decoding
Sparsity
constraint
X
Z
Code
Input
Code prediction
Code energy
Decoding energy
Input decoding
Sparsity
constraint
X
Z
(C)
0 0.5 1 1.5 2
0.05
0.1
0.15
Entropy (bits/pixel) (D)
(E) (F)
(G) (H)
Figure 1: (A)-(B) Error rate on MNIST training (with 10, 100 a
test set produced by a linear classifier trained on the codes produ
The entropy and RMSE refers to a quantization into 256 bins. The
also to the same classifier trained on raw pixel data (showing the a
The error bars refer to 1 std. dev. of the error rate for 10 rand
(same splits for all methods). The parameter αs in eq. 8 takes va
Comparison between SESM, RBM, and PCA when quantizing the
Random selection from the 200 linear filters that were learned by SE
of original and reconstructed digit from the code produced by the
propagation through encoder and decoder). (F) Random selection
Back-projection in image space of the filters learned in the second
extractor. The second stage was trained on the non linearly transfor
stage machine. The back-projection has been performed by using a
machine, and propagating this through the second stage decoder an
at the second stage discover the class-prototypes (manually order
though no class label was ever used during training. (H) Feature ex
patches: some filters that were learned.
(A)
0 1 2
0
5
10
15
20
25
30
35
40
45
ENTROPY (bits/pixel)
ERRORRATE%
10 samples
0 1 2
0
2
4
6
8
10
12
14
16
18
ENTROPY (bits/pixel)
ERRORRATE%
100 samples
0 1 2
3
4
5
6
7
8
9
10
ENTROPY (bits/pixel)
ERRORRATE%
1000 samples
RAW: train
RAW: test
PCA: train
PCA: test
RBM: train
RBM: test
SESM: train
SESM: test
(B)
0 0.2 0.4
0
5
10
15
20
25
30
35
40
45
RMSE
ERRORRATE%
10 samples
0 0.2 0.4
0
2
4
6
8
10
12
14
16
18
RMSE
ERRORRATE%
100 samples
0 0.2 0.4
3
4
5
6
7
8
9
10
RMSE
ERRORRATE%
1000 samples
(C)
0 0.5 1 1.5 2
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
RMSE
Entropy (bits/pixel)
Symmetric Sparse Coding − RBM − PCA
PCA: quantization in 5 bins
PCA: quantization in 256 bins
RBM: quantization in 5 bins
RBM: quantization in 256 bins
Sparse Coding: quantization in 5 bins
Sparse Coding: quantization in 256 bins
(D)
Layer 1: Matrix W1 of size 192 x 784
192 sparse bases of 28 x 28 pixels
Layer 2: Matrix W2 of size 10 x 192
10 sparse bases of 192 units
[Ranzato, Boureau & LeCun, “Sparse Feature Learning for Deep Belief Networks ”, NIPS, 2007]

32. Our results:
bases learned on layer 1

33. Our results:
back-­‐‑projecting layer 2

34. Sparse representations
Layer 1
Layer 2

35. Semantic Hashing
[Hinton & Salakhutdinov, “Reducing the dimensionality of data with neural networks, Science, 2006;
Salakhutdinov & Hinton, “Semantic Hashing”, Int J Approx Reason, 2007]
2000
500
250
125
2
125
250
500
2000

36. Beyond auto-­‐‑encoders
for web search (MSR)
[Huang, He, Gao, Deng et al, “Learning Deep Structured Semantic Models for Web Search using Clickthrough Data”, CIKM, 2013]
s: “racing car”Input word/phrase
dim = 5MBag-of-words vector
dim = 50K
d=500Letter-tri-gram
embedding matrix
Letter-tri-gram coeff.
matrix (fixed)
d=500
Semantic
vector
d=300
t1: “formula one”
dim = 5M
dim = 50K
d=500
d=500
d=300
t2: “ford model t”
dim = 5M
dim = 50K
d=500
d=500
d=300
Compute Cosine similarity
between semantic vectors cos(s,t1) cos(s,t2)
W1
W2
W3
W4