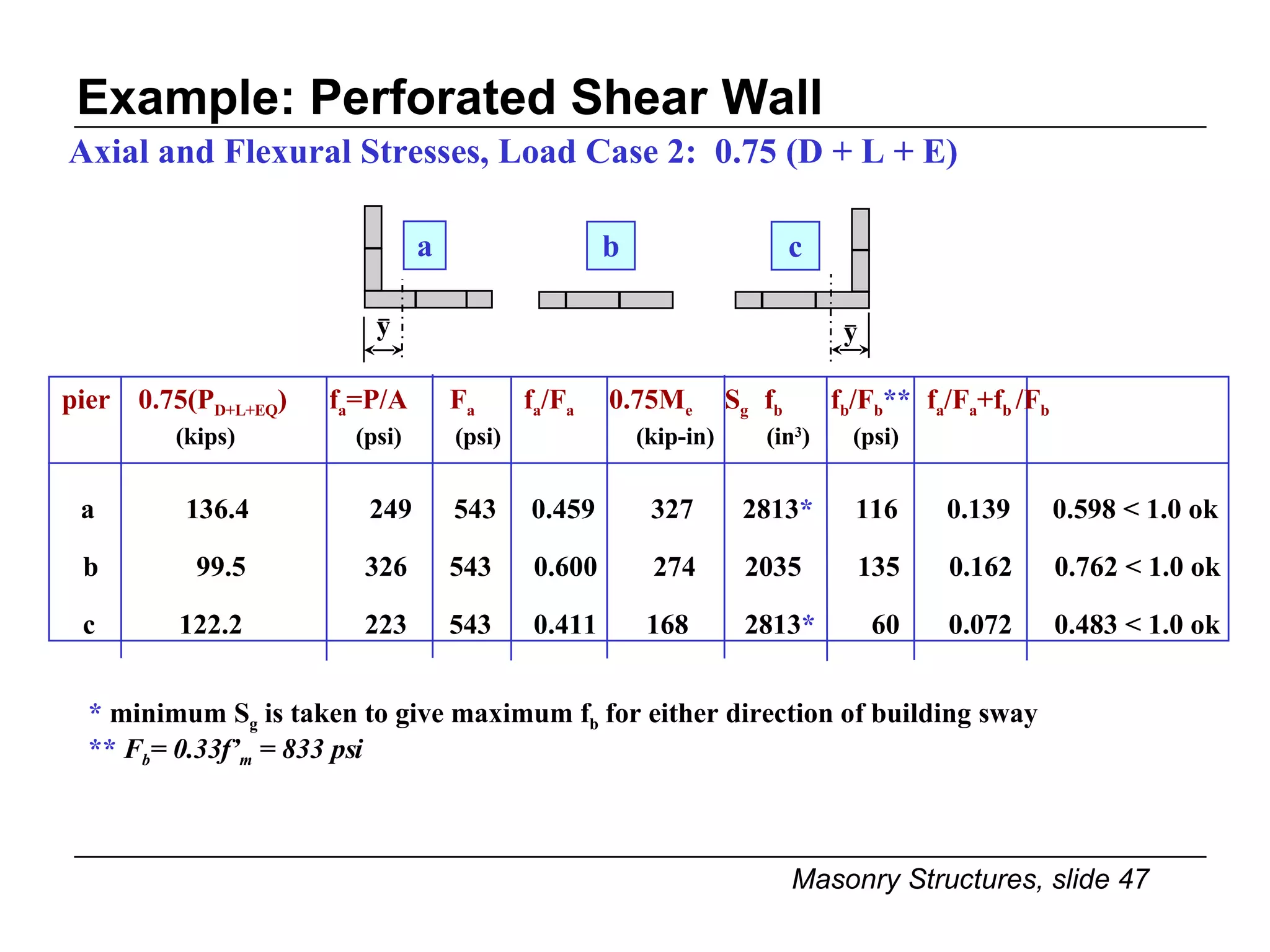
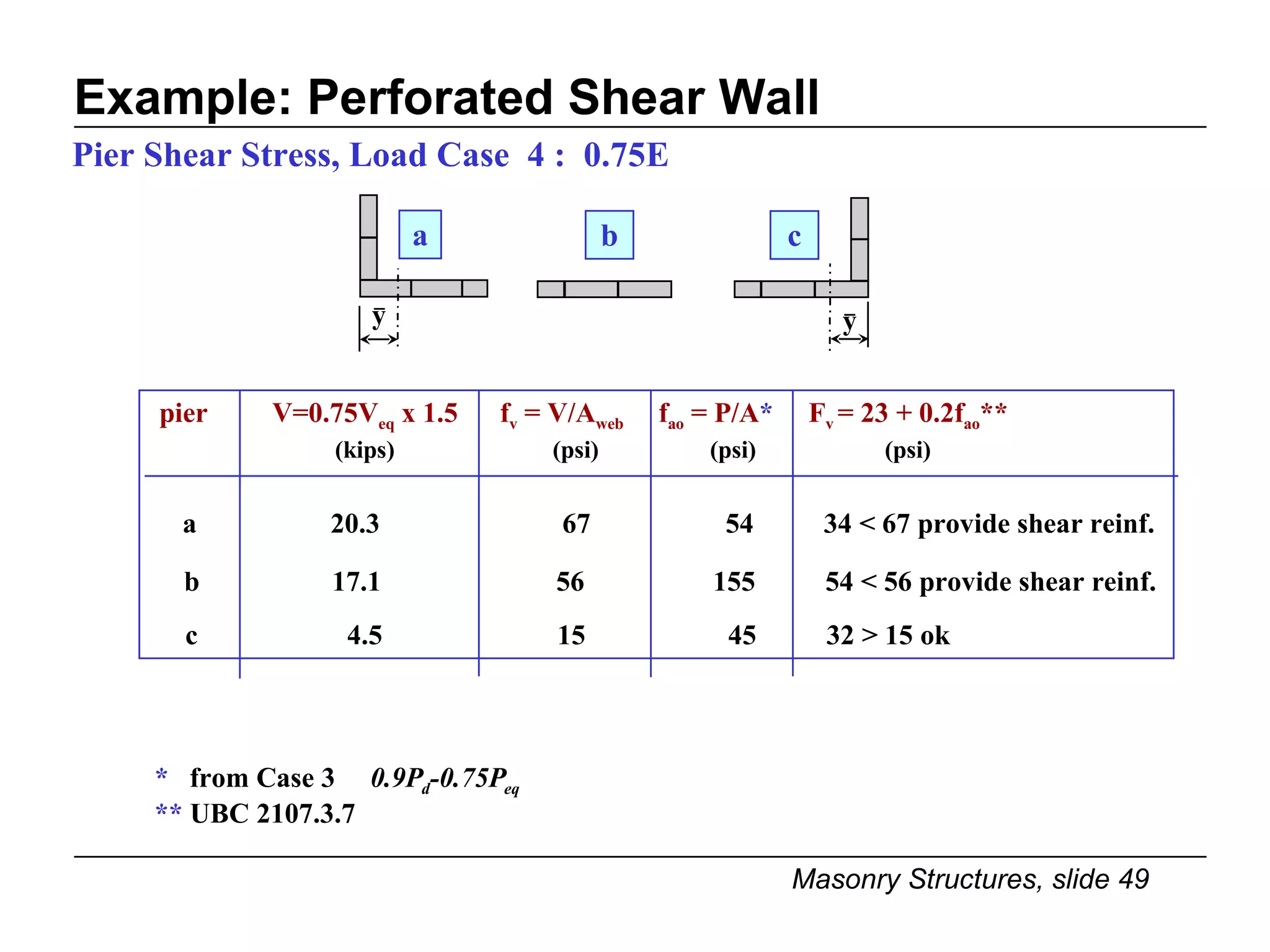
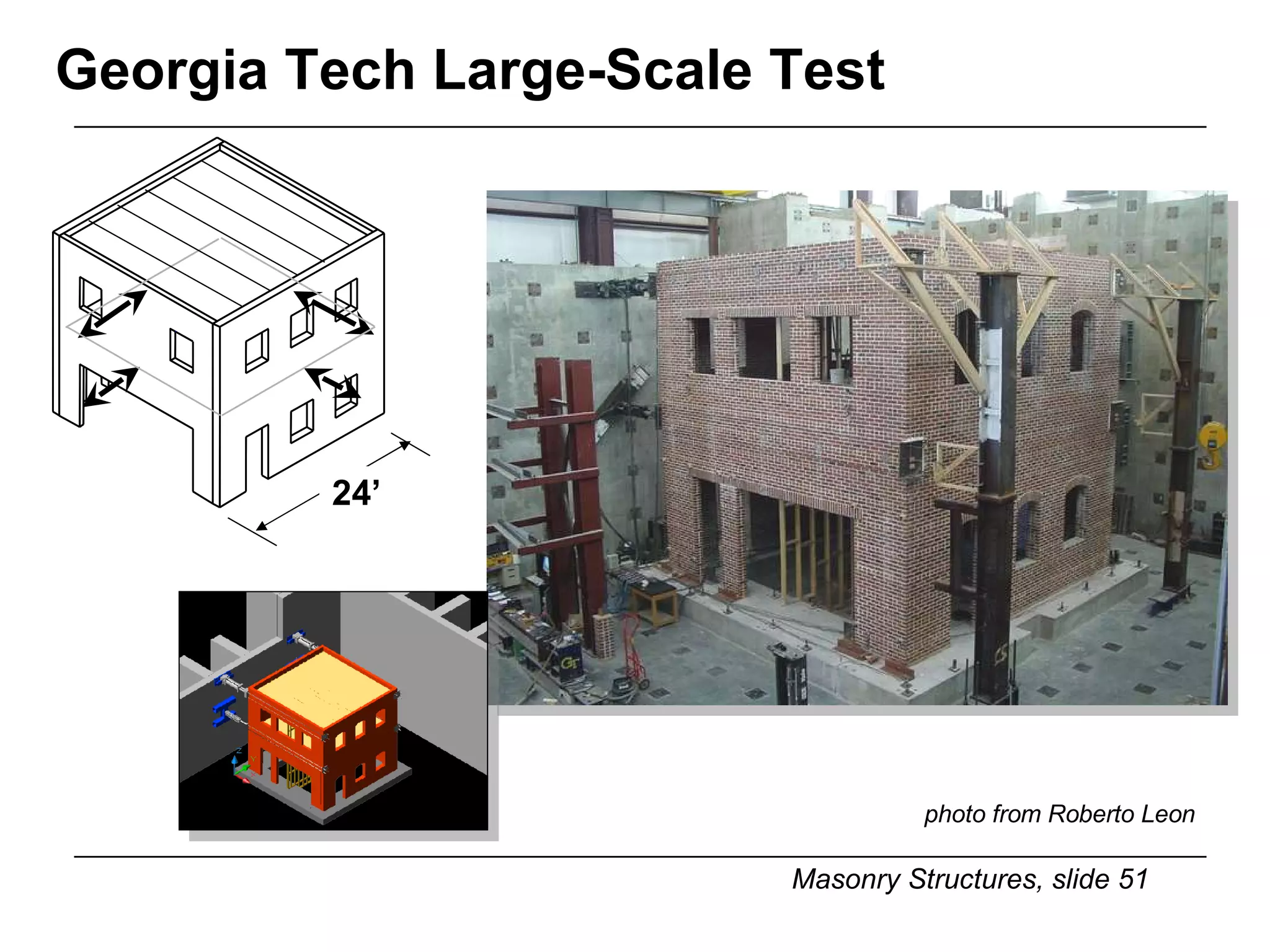
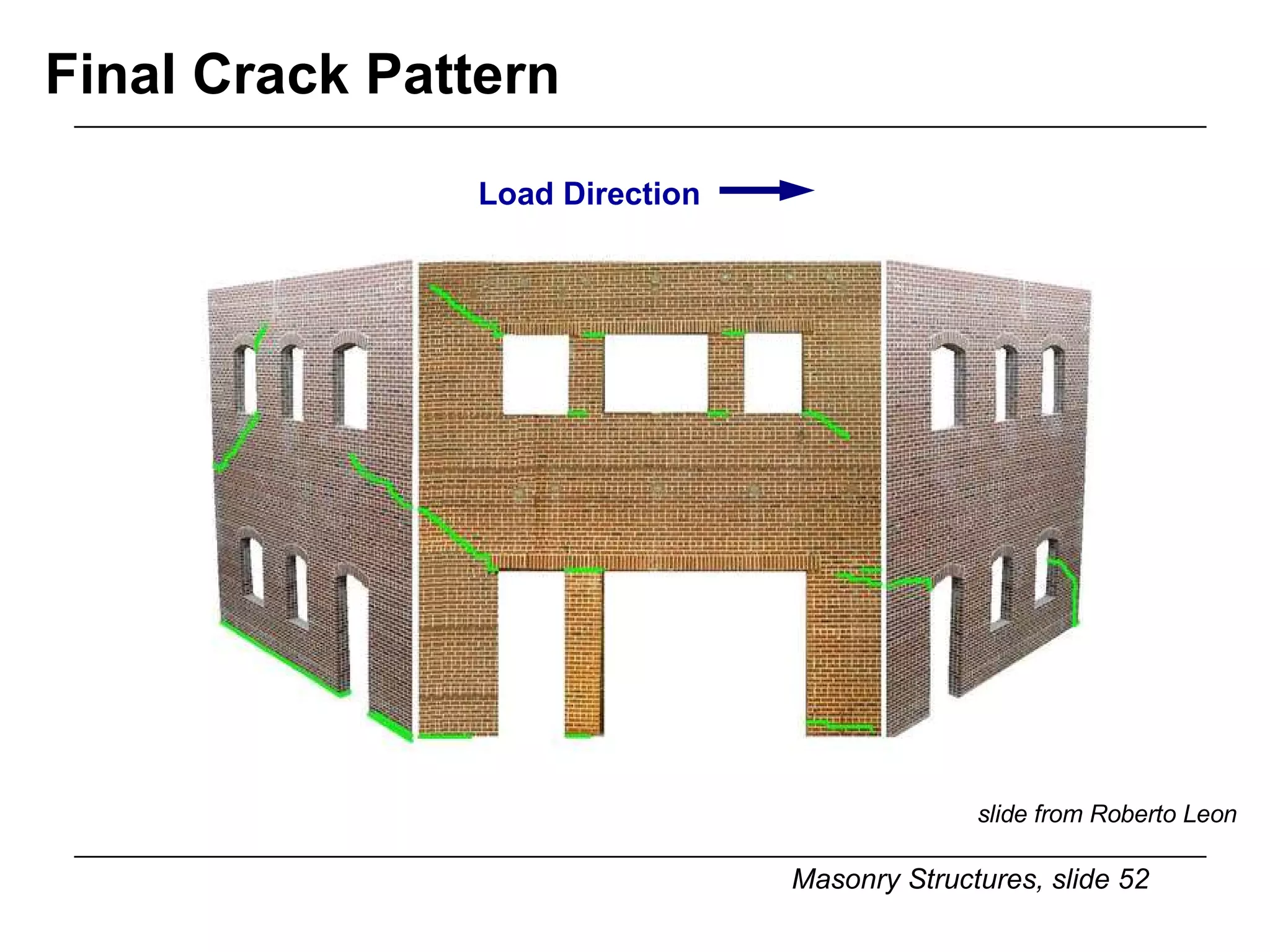
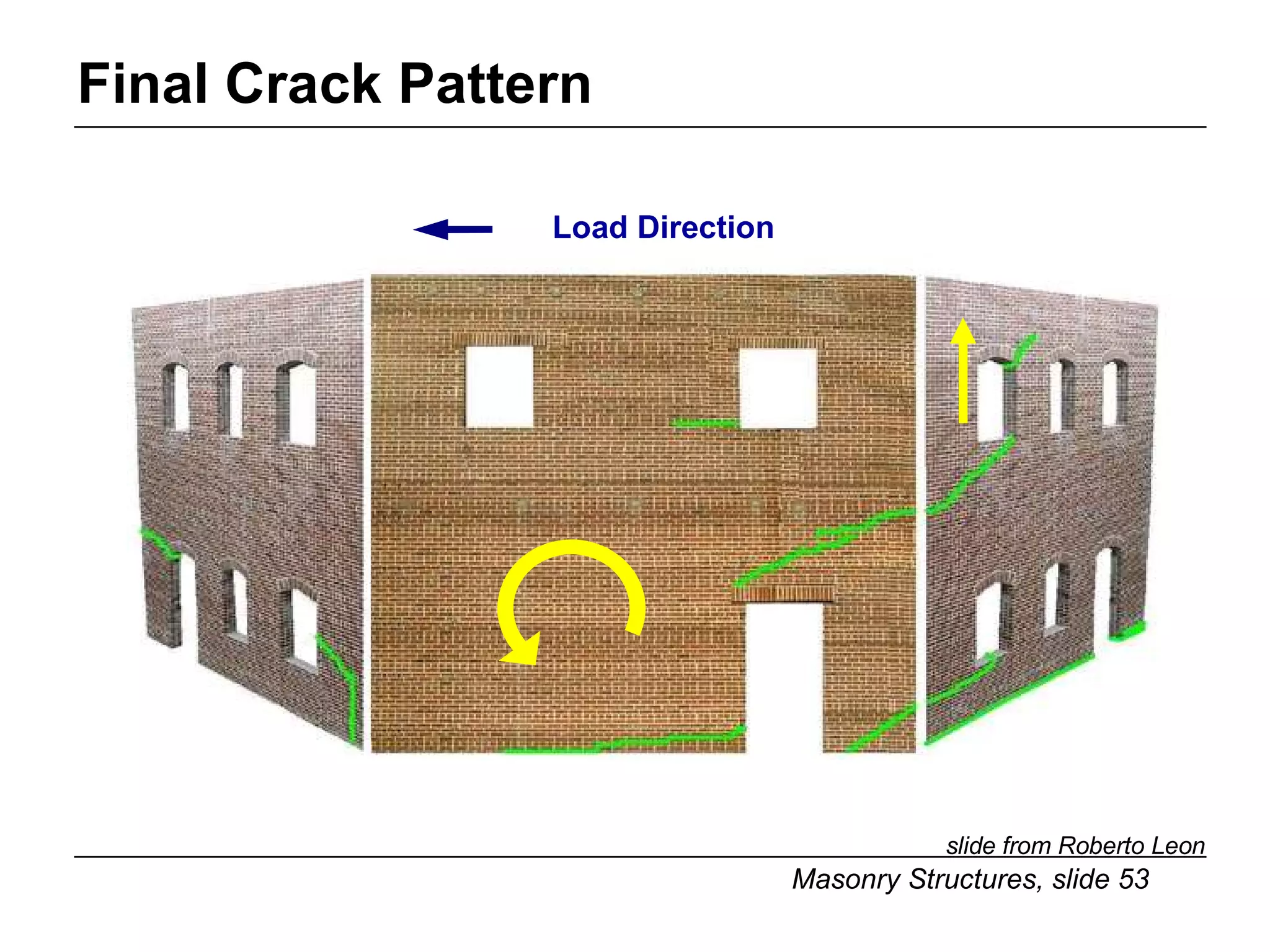
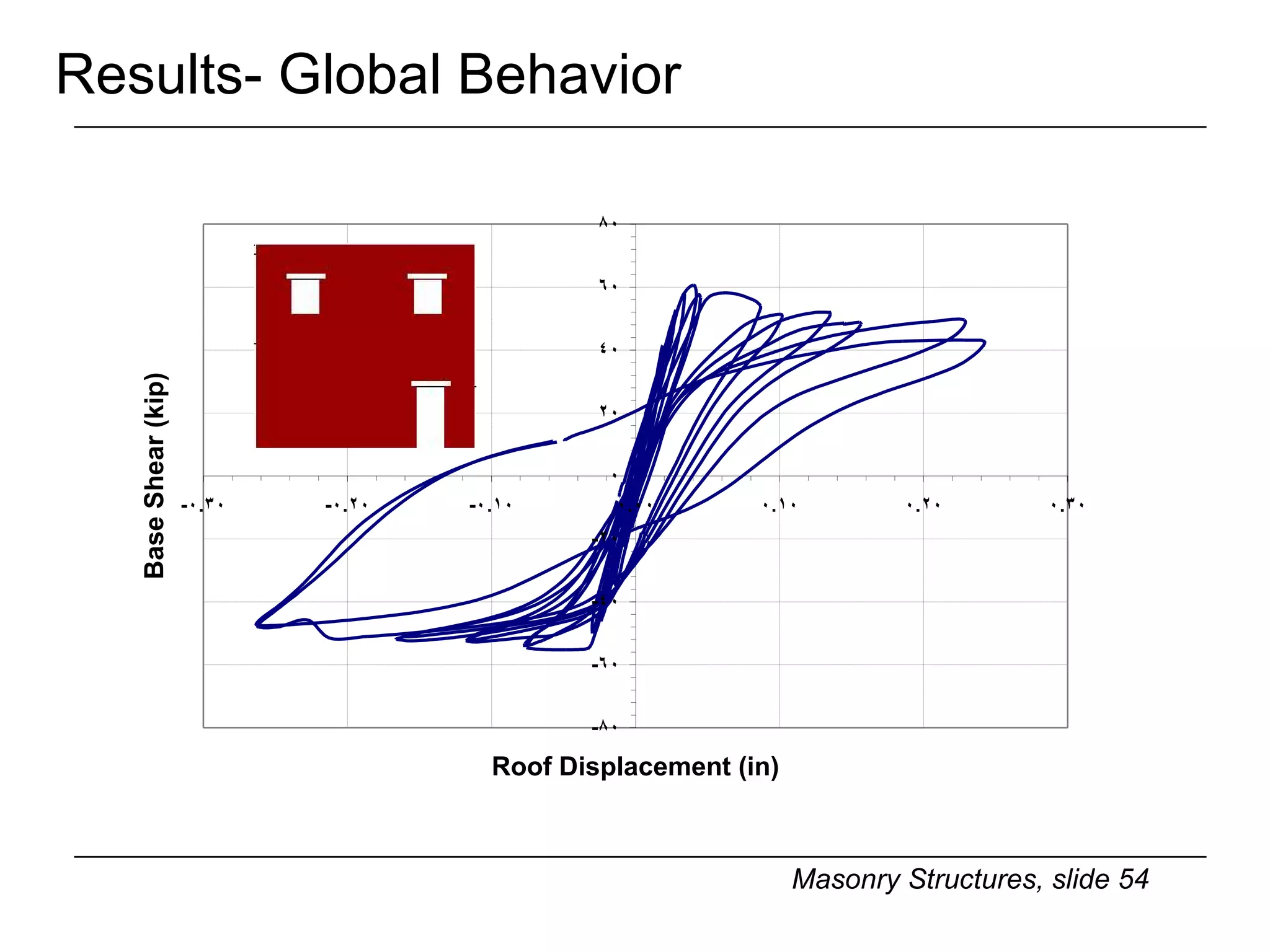
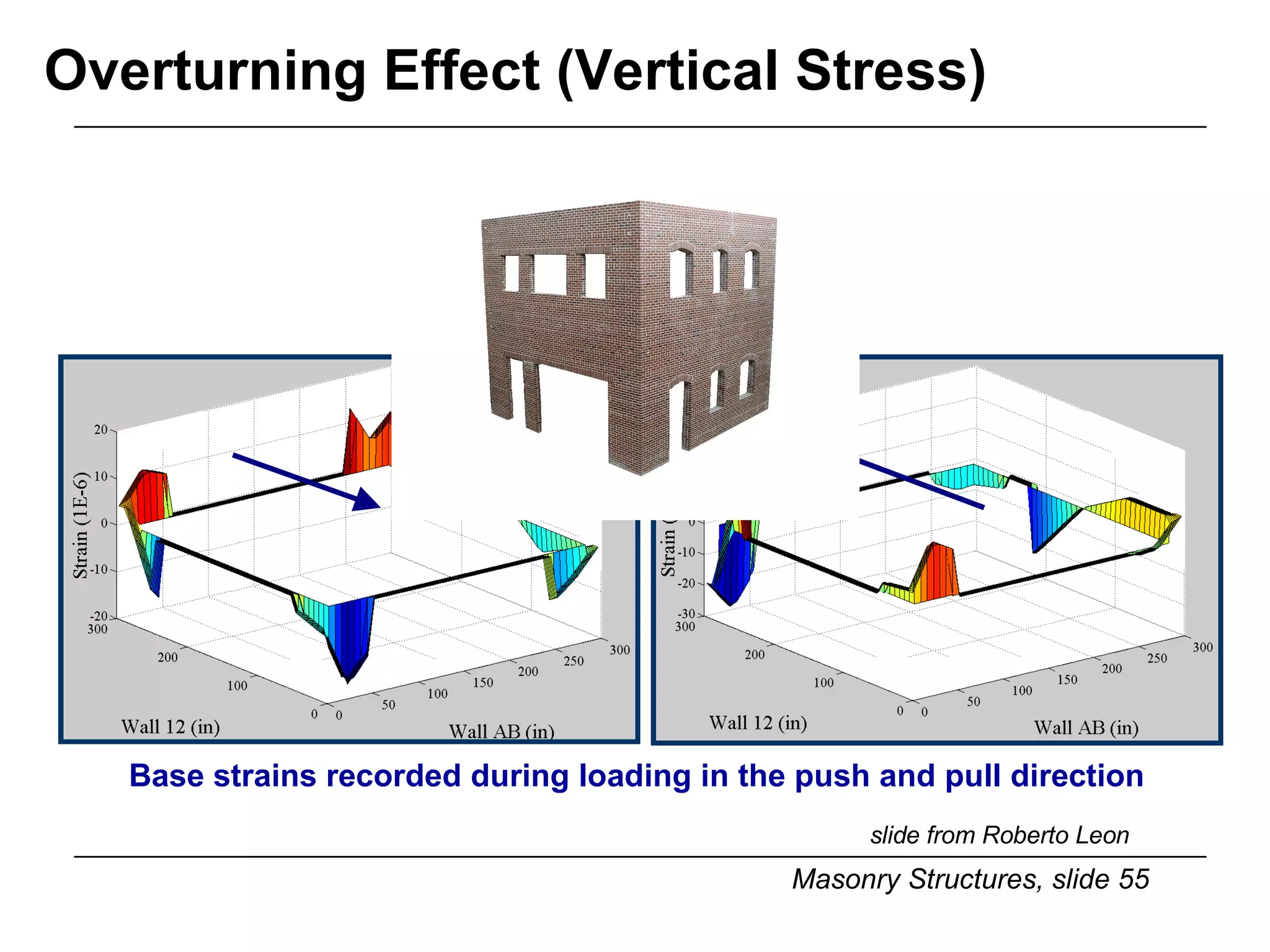
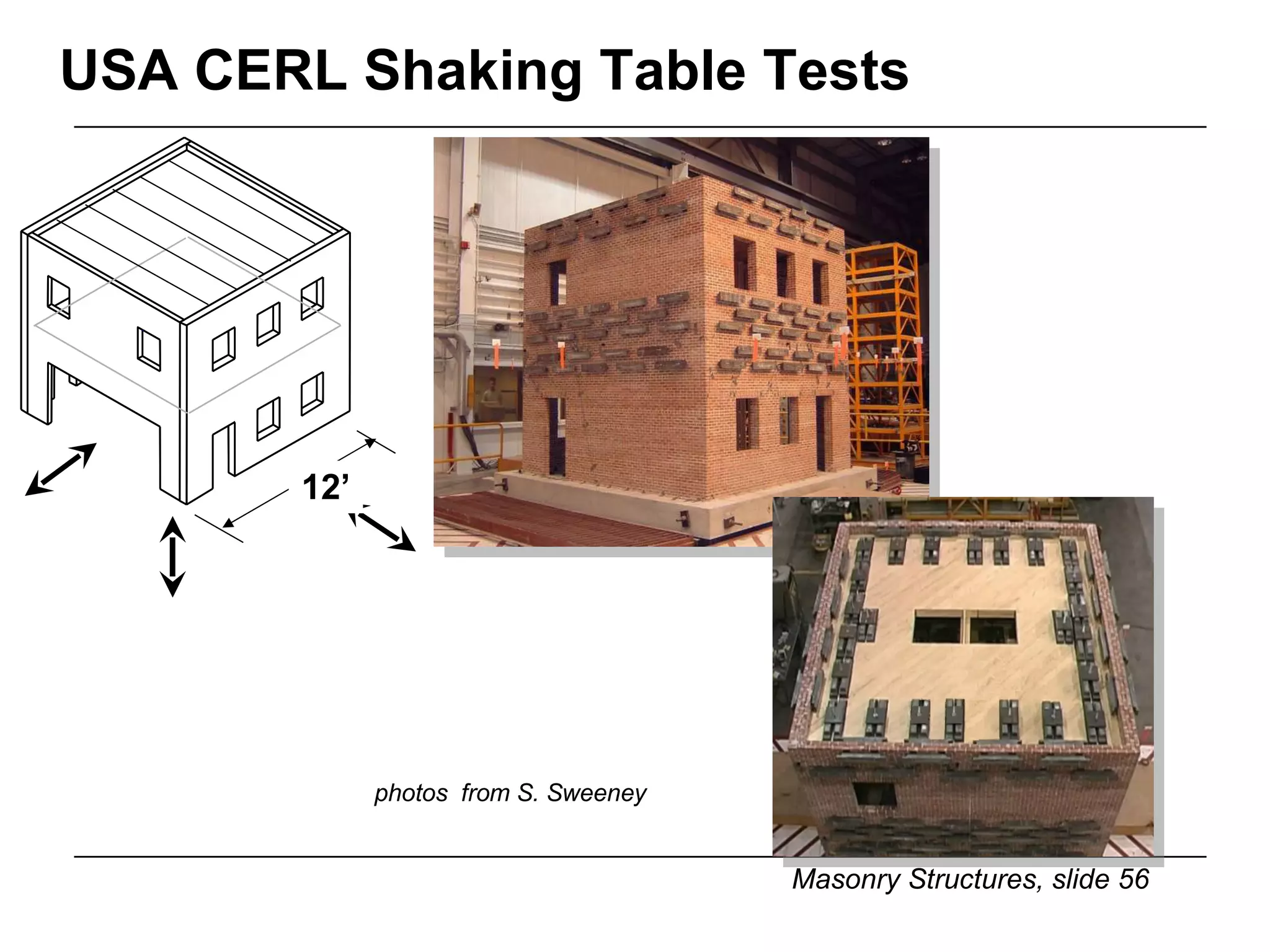
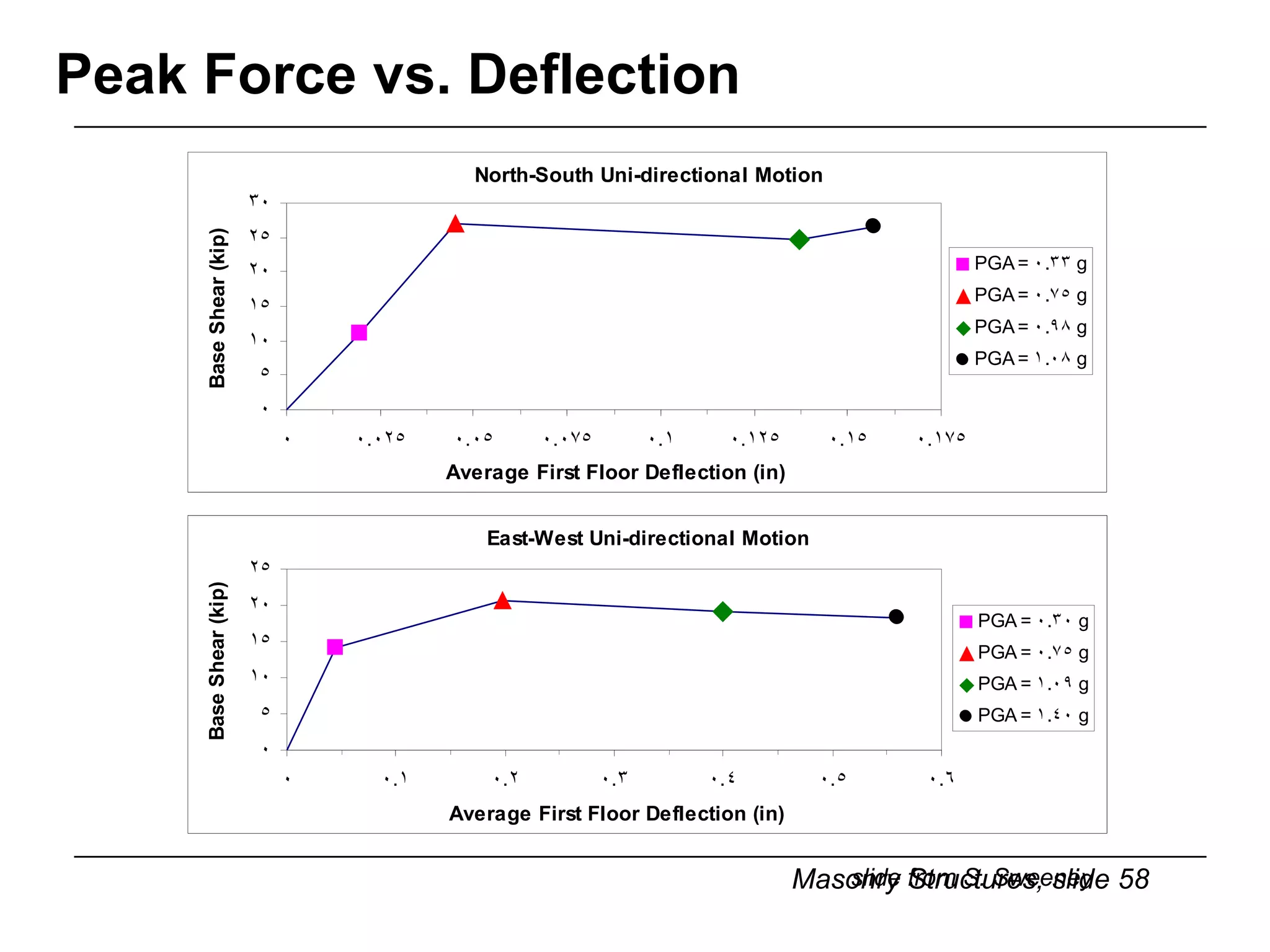
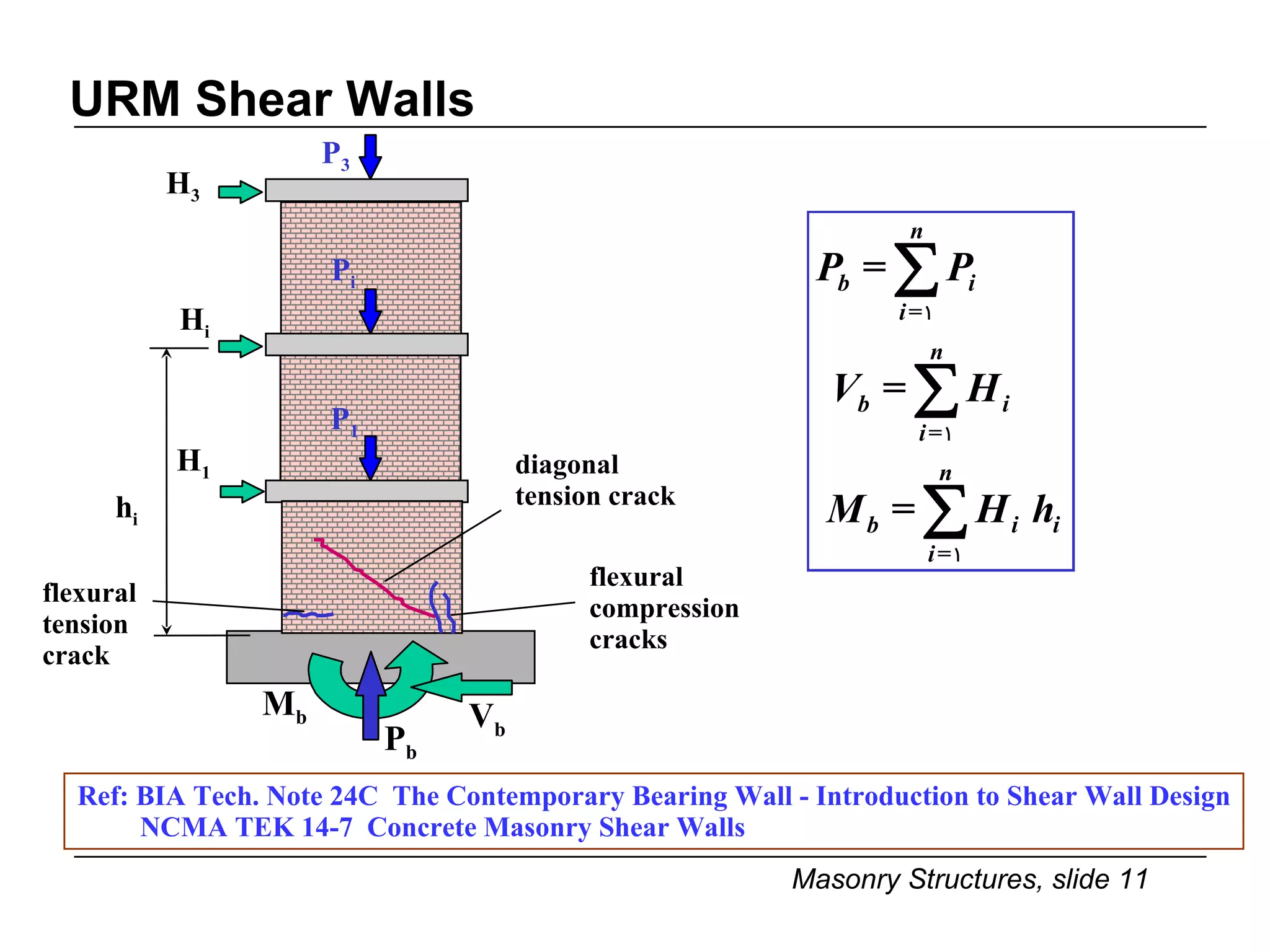
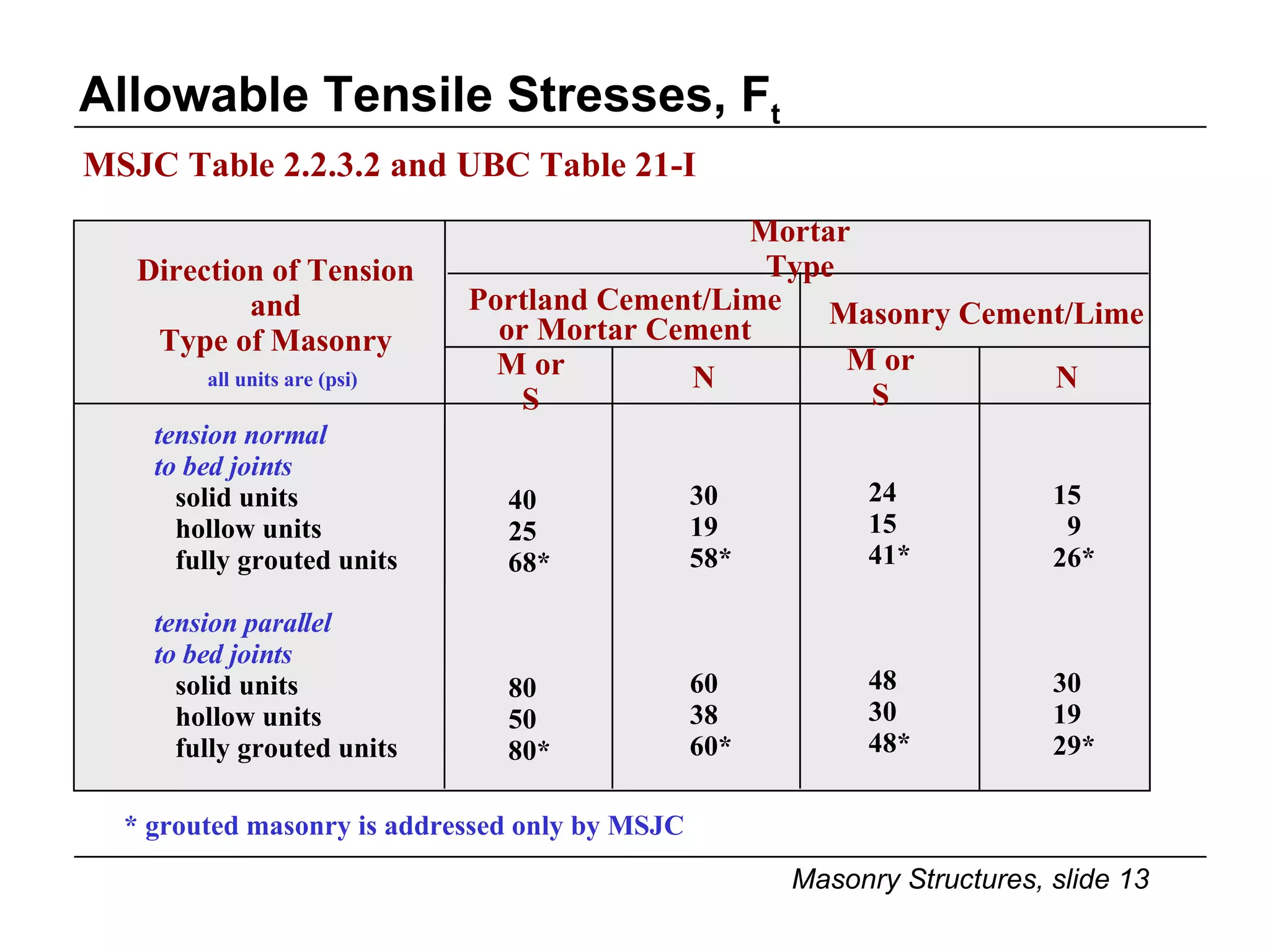
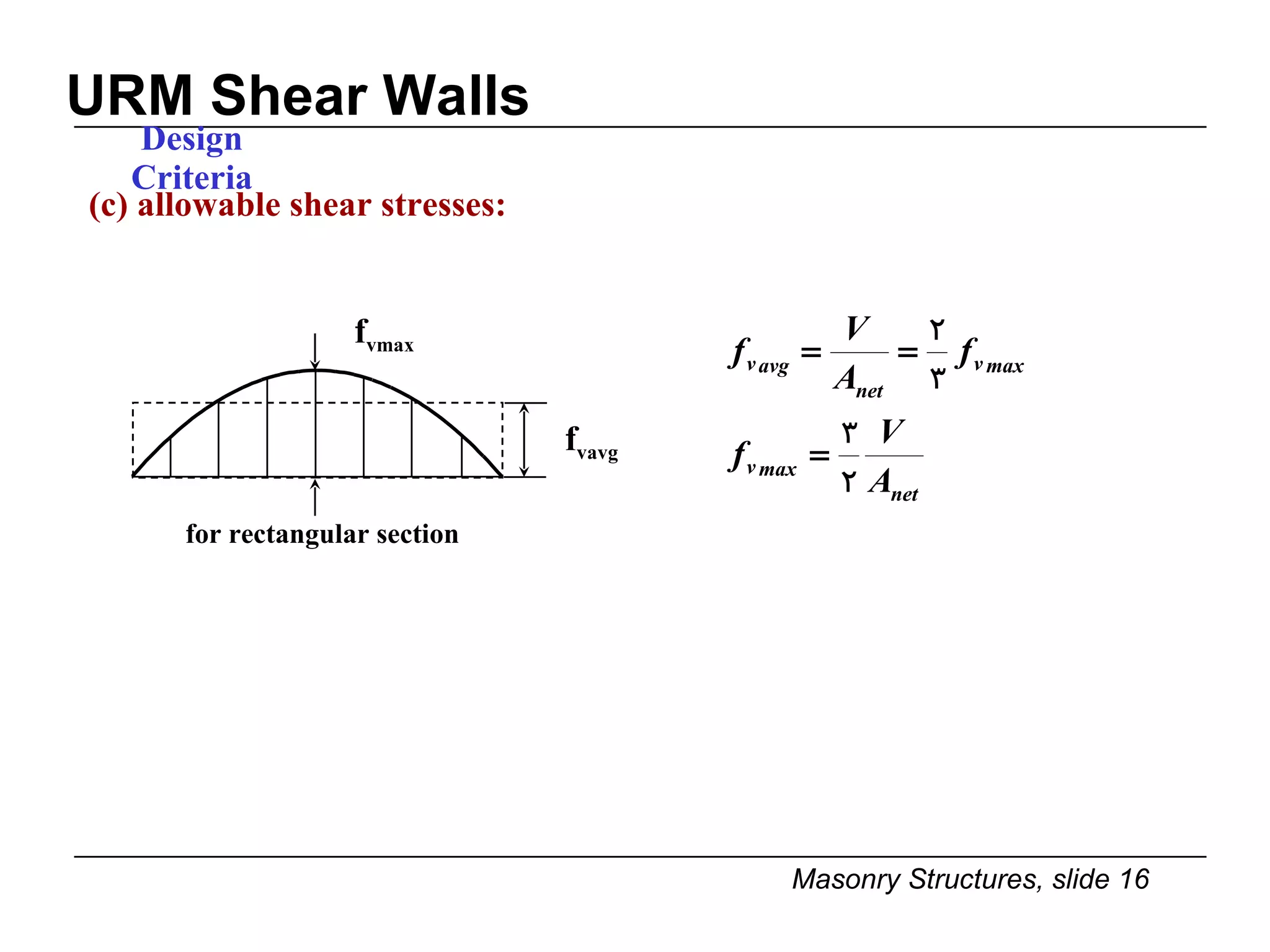
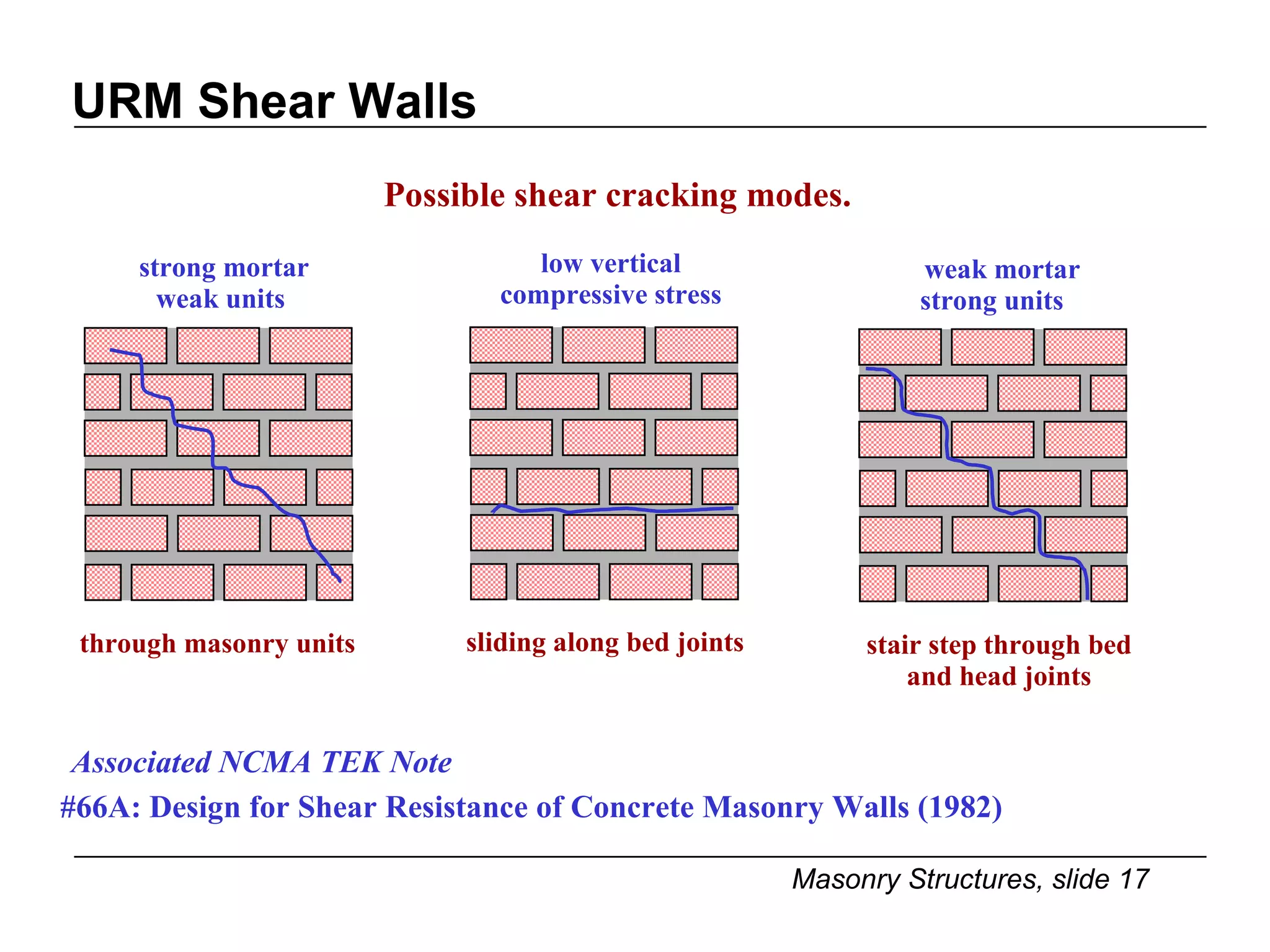
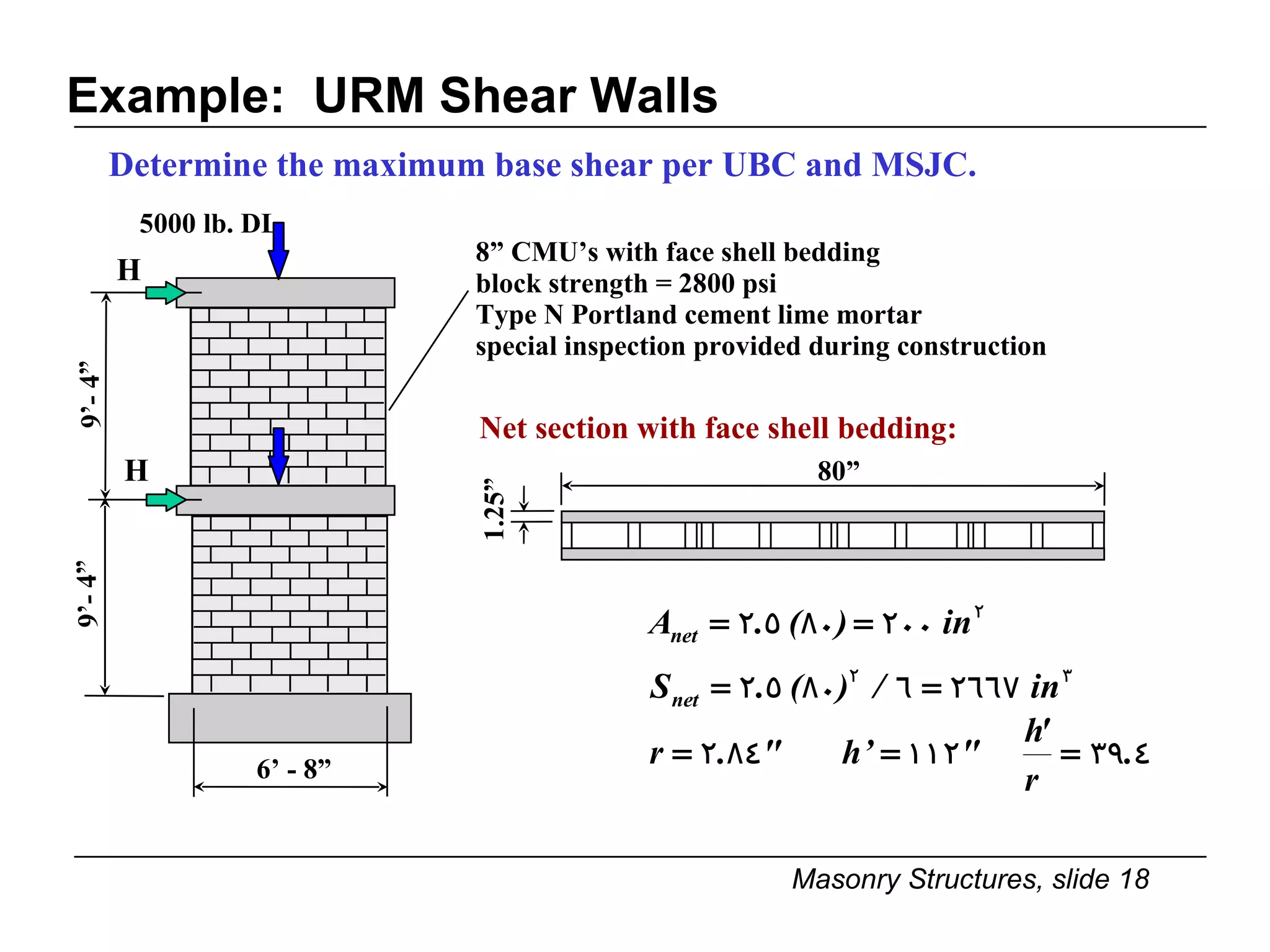
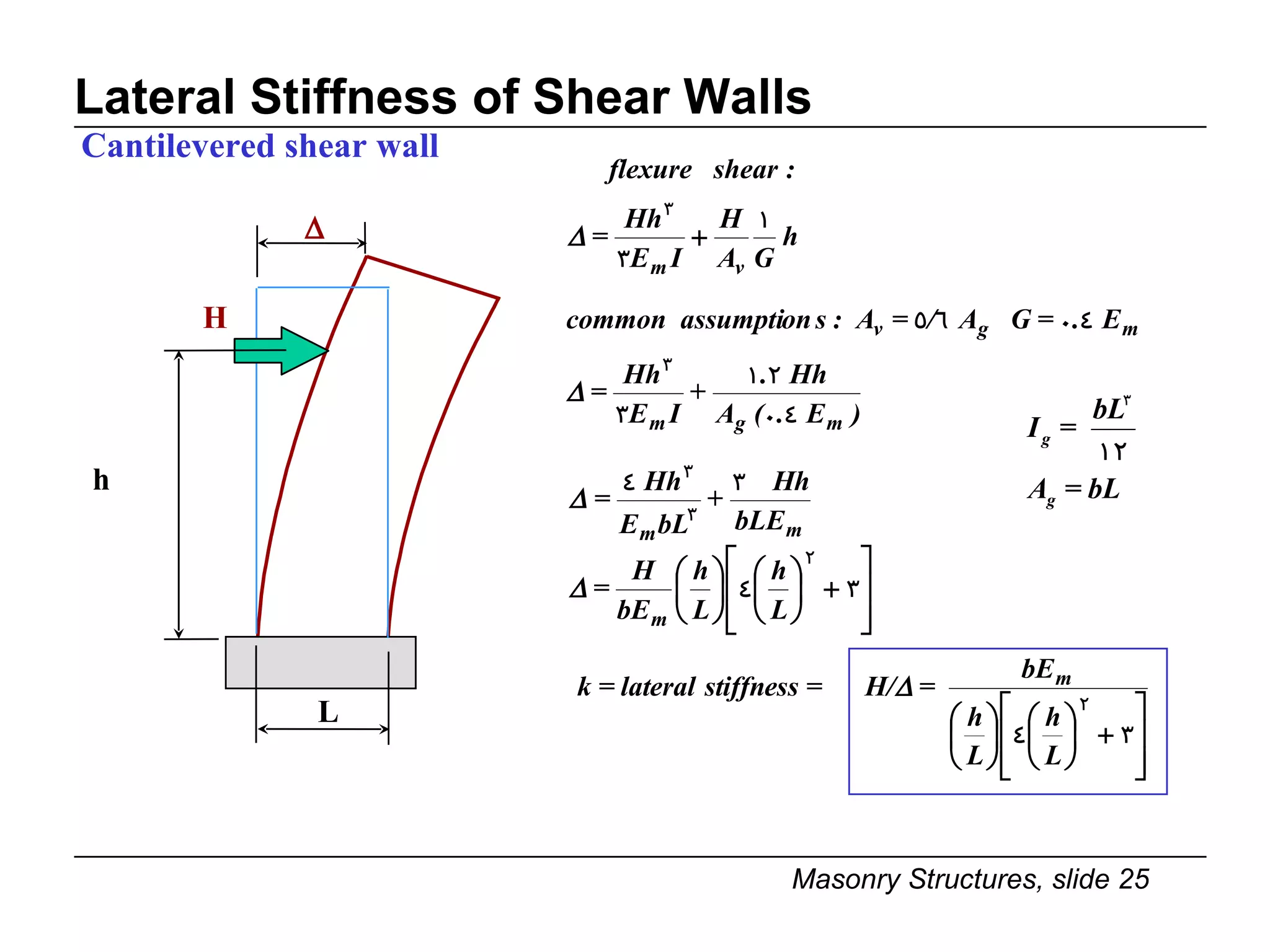
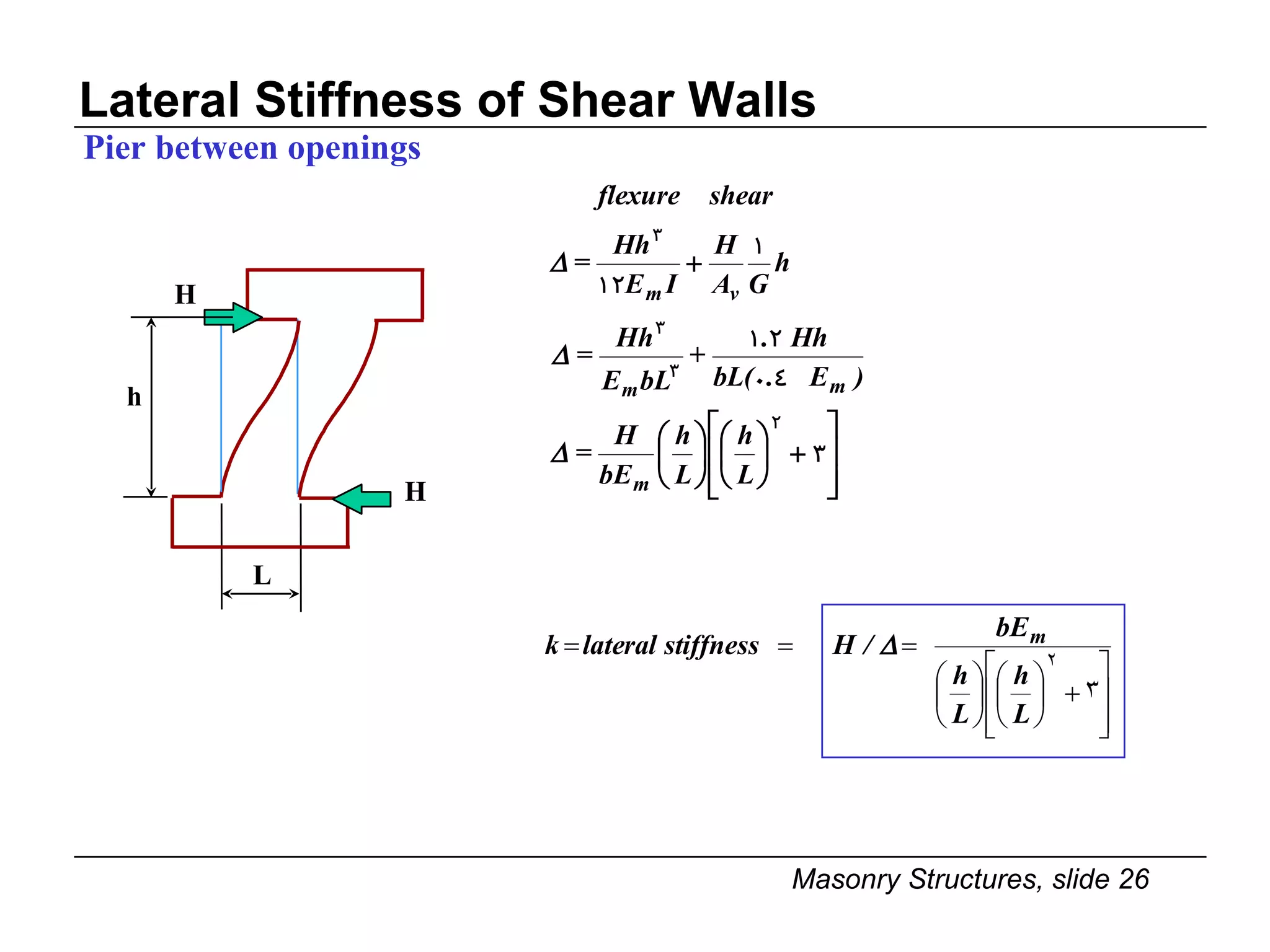
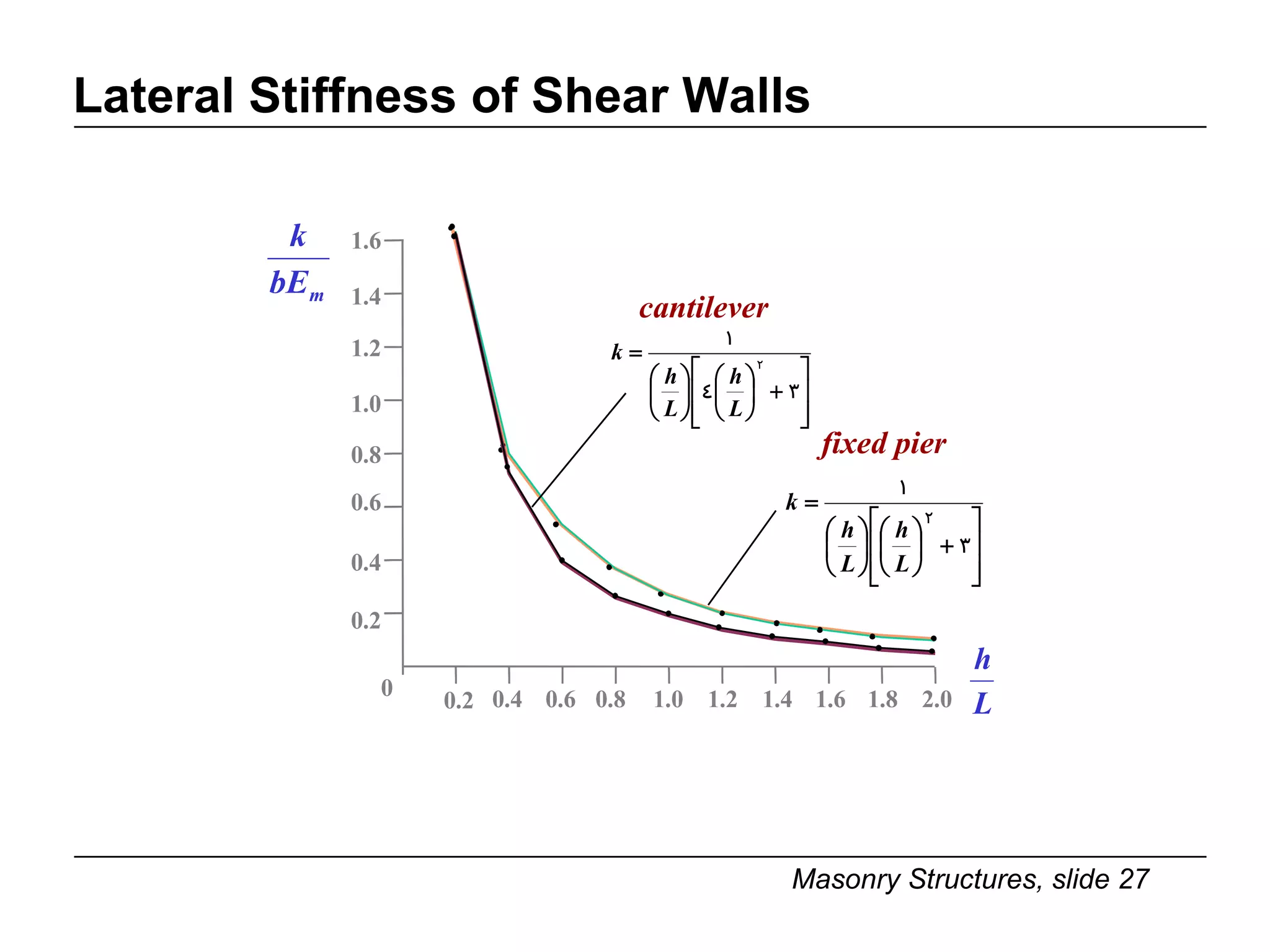
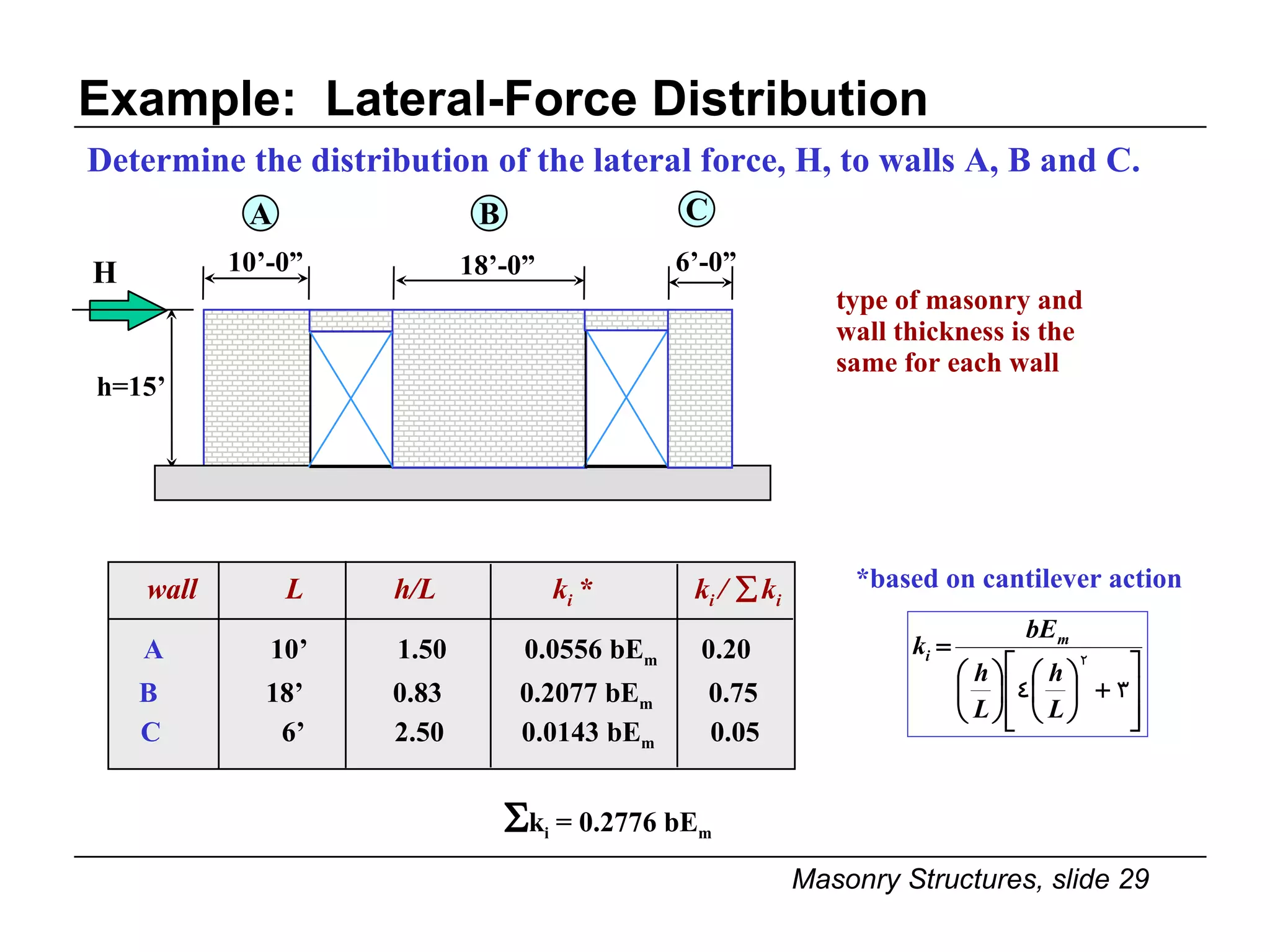
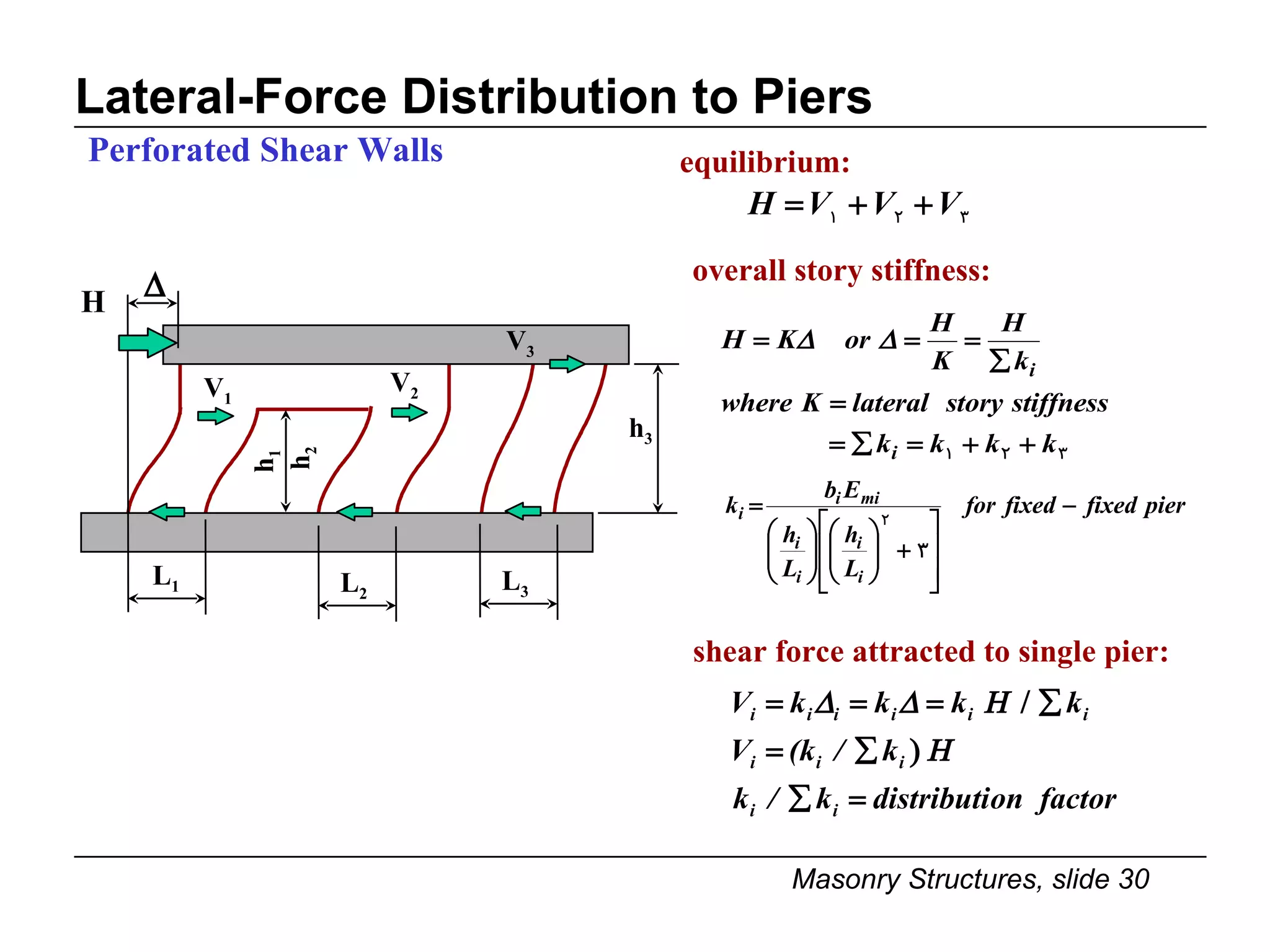
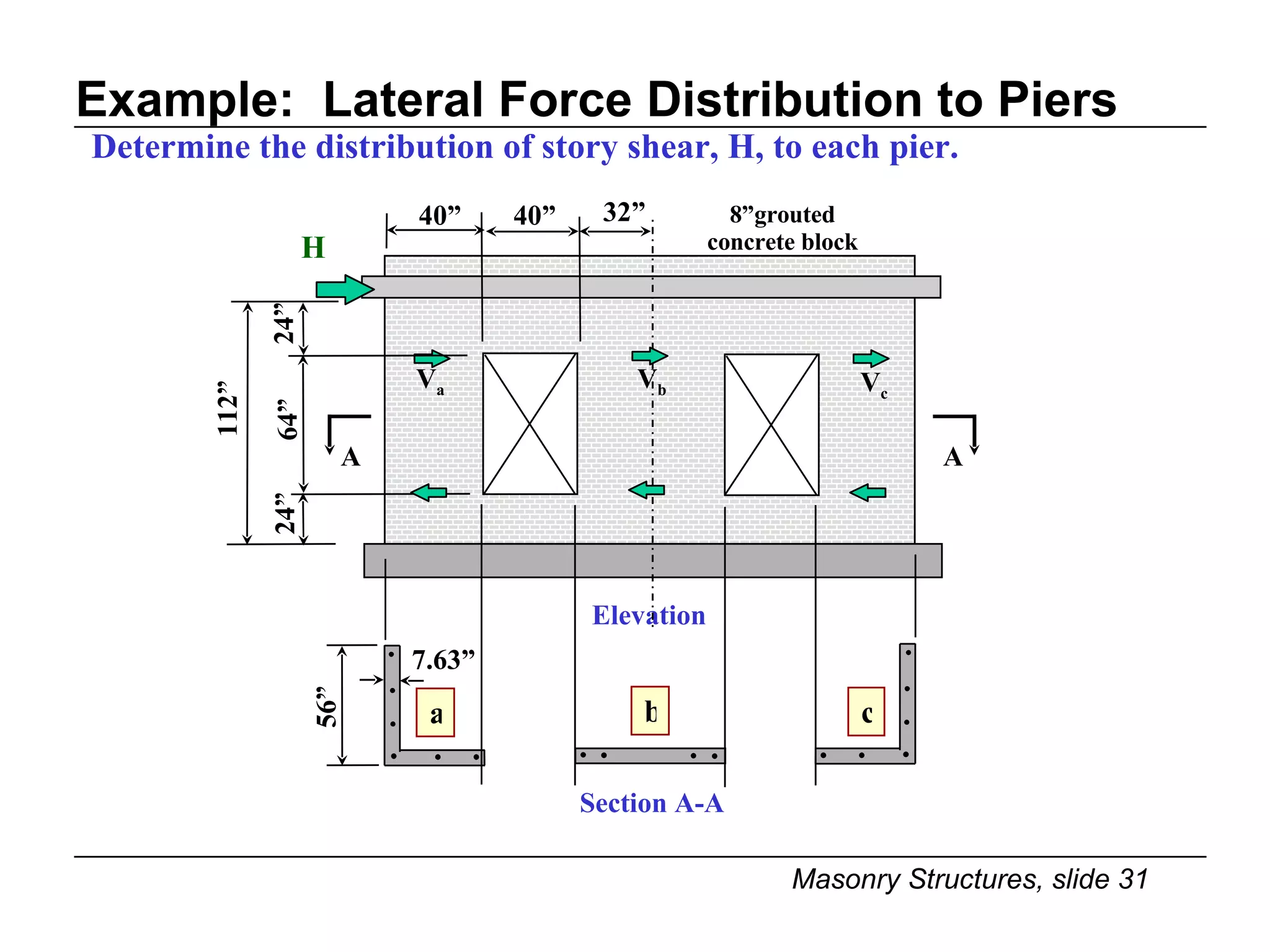
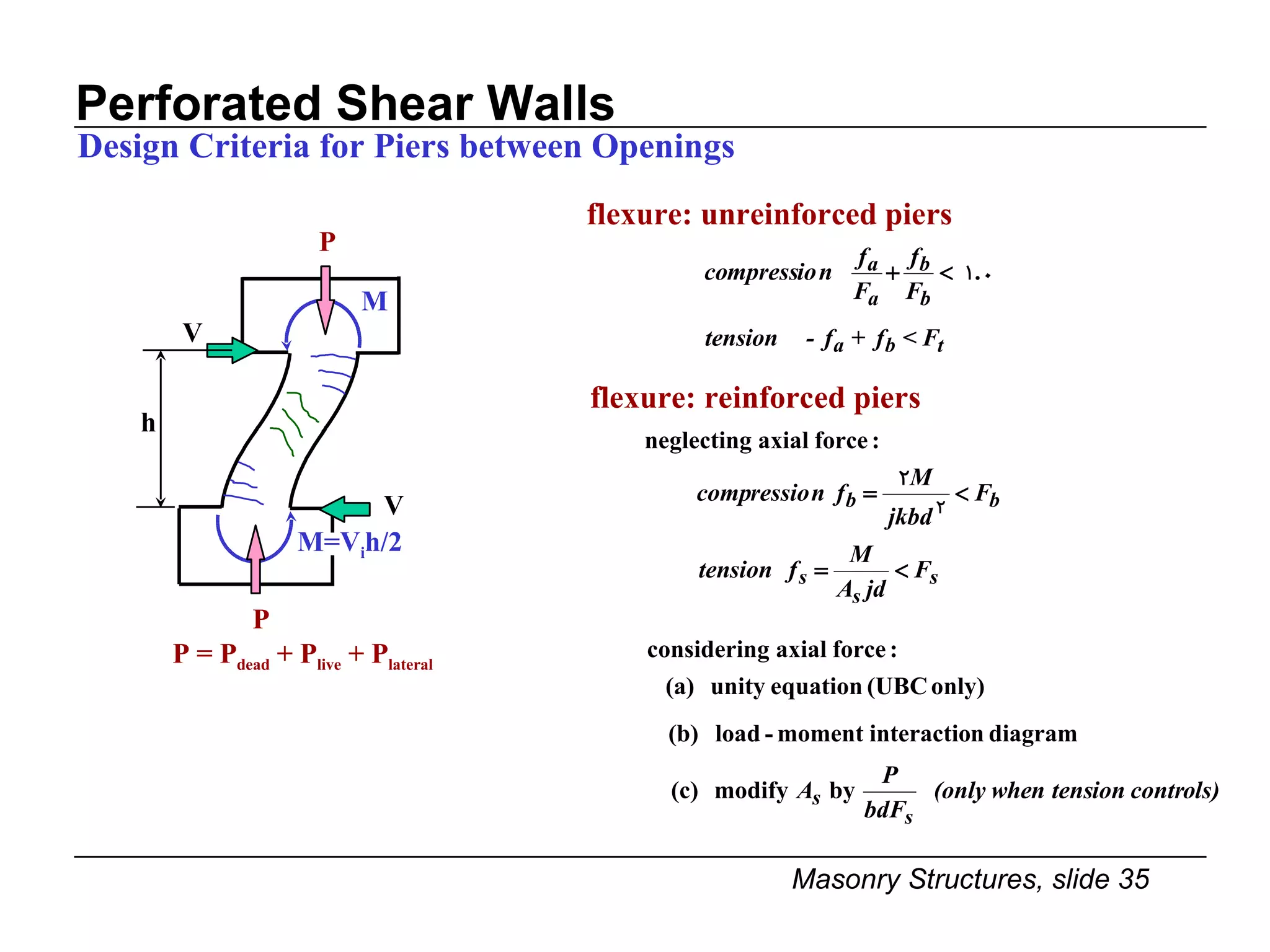
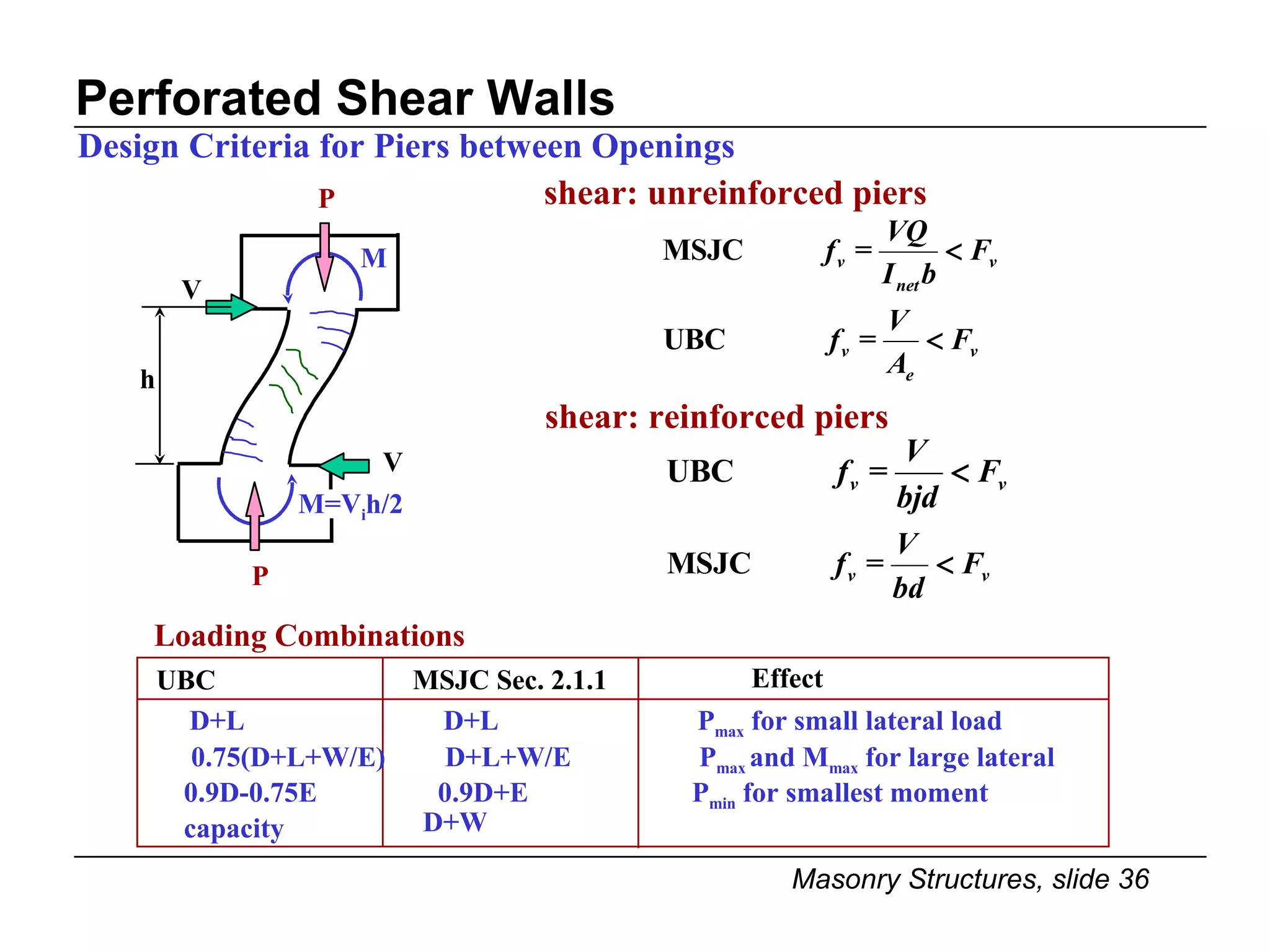
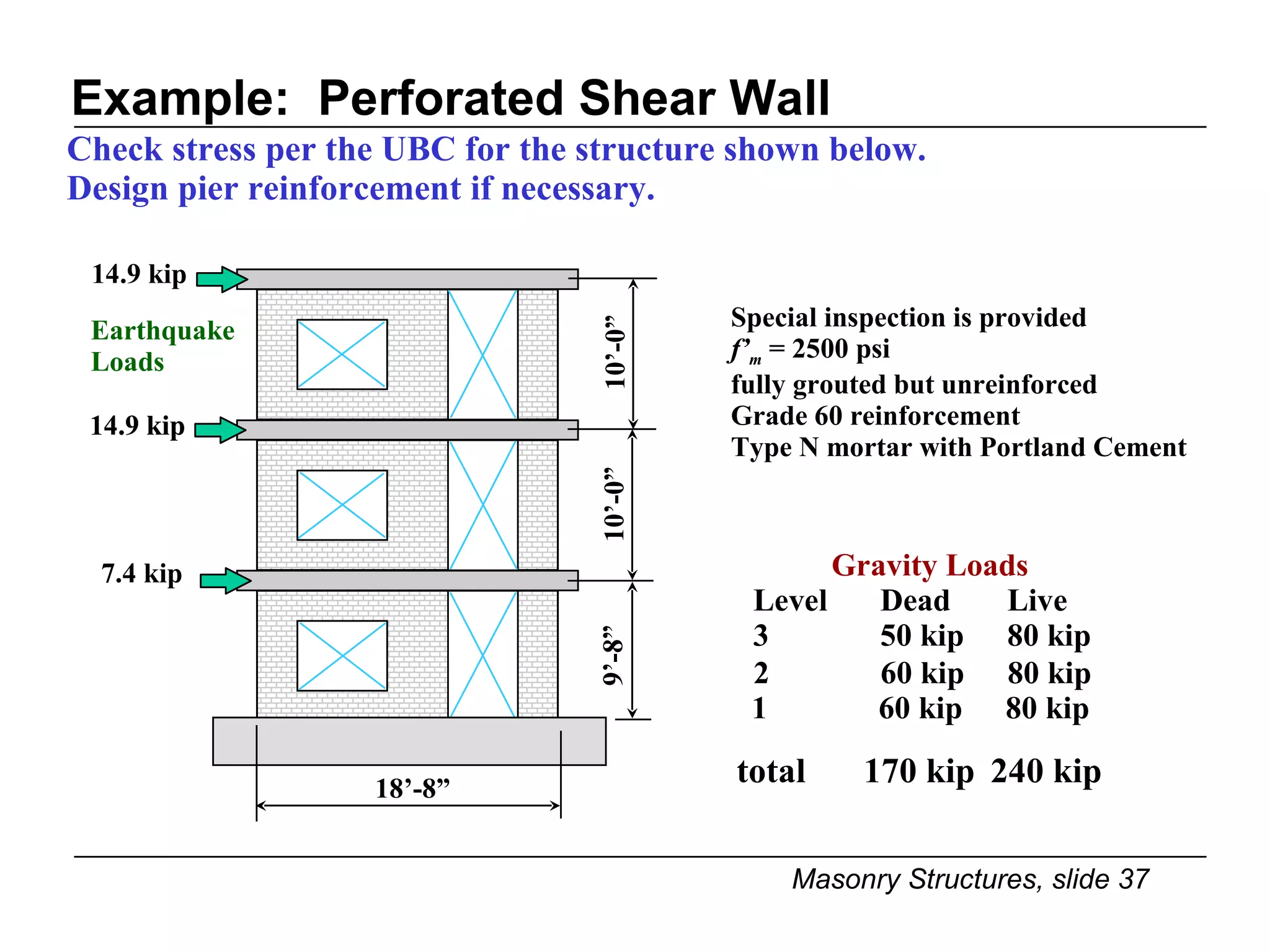
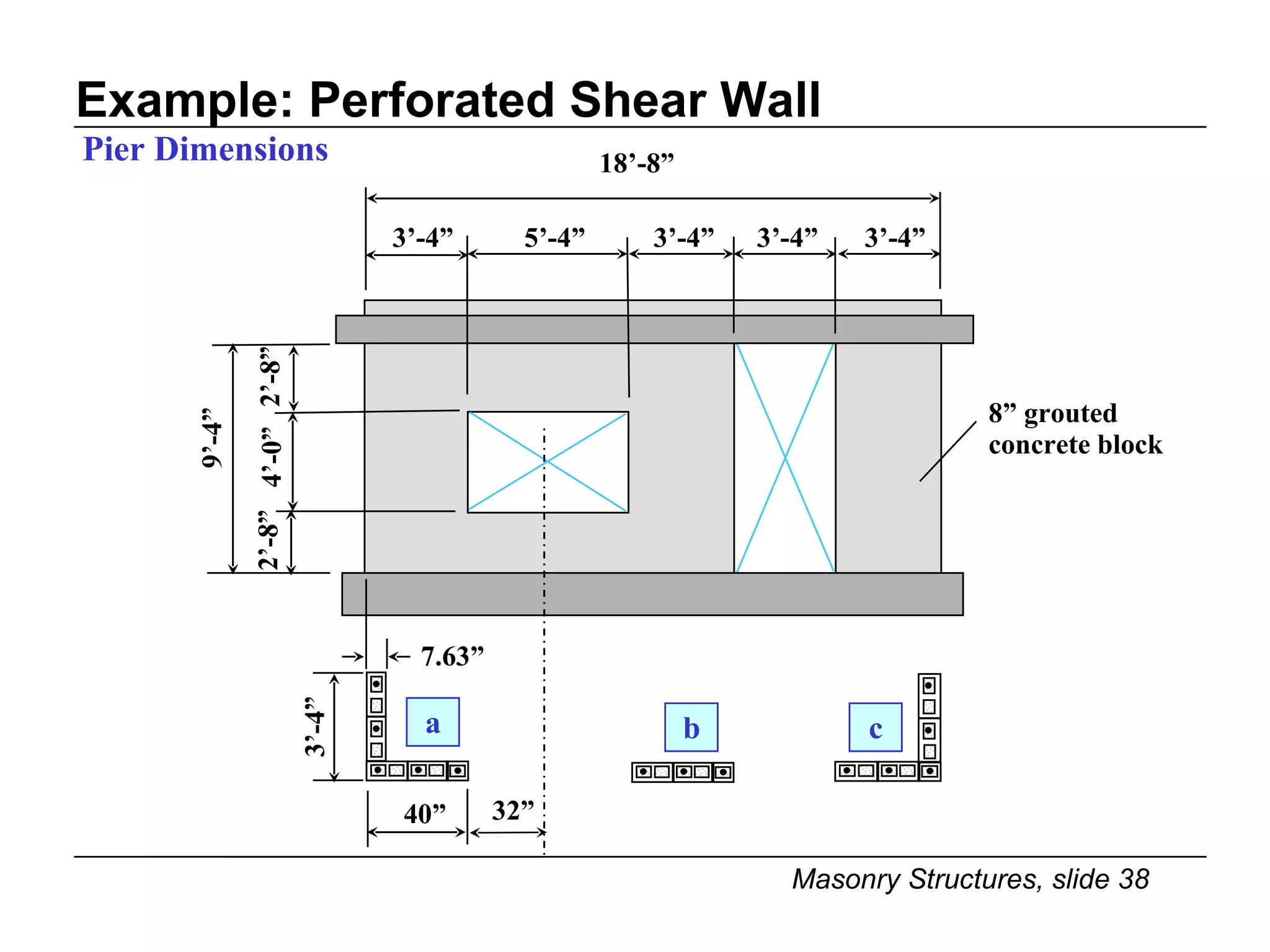
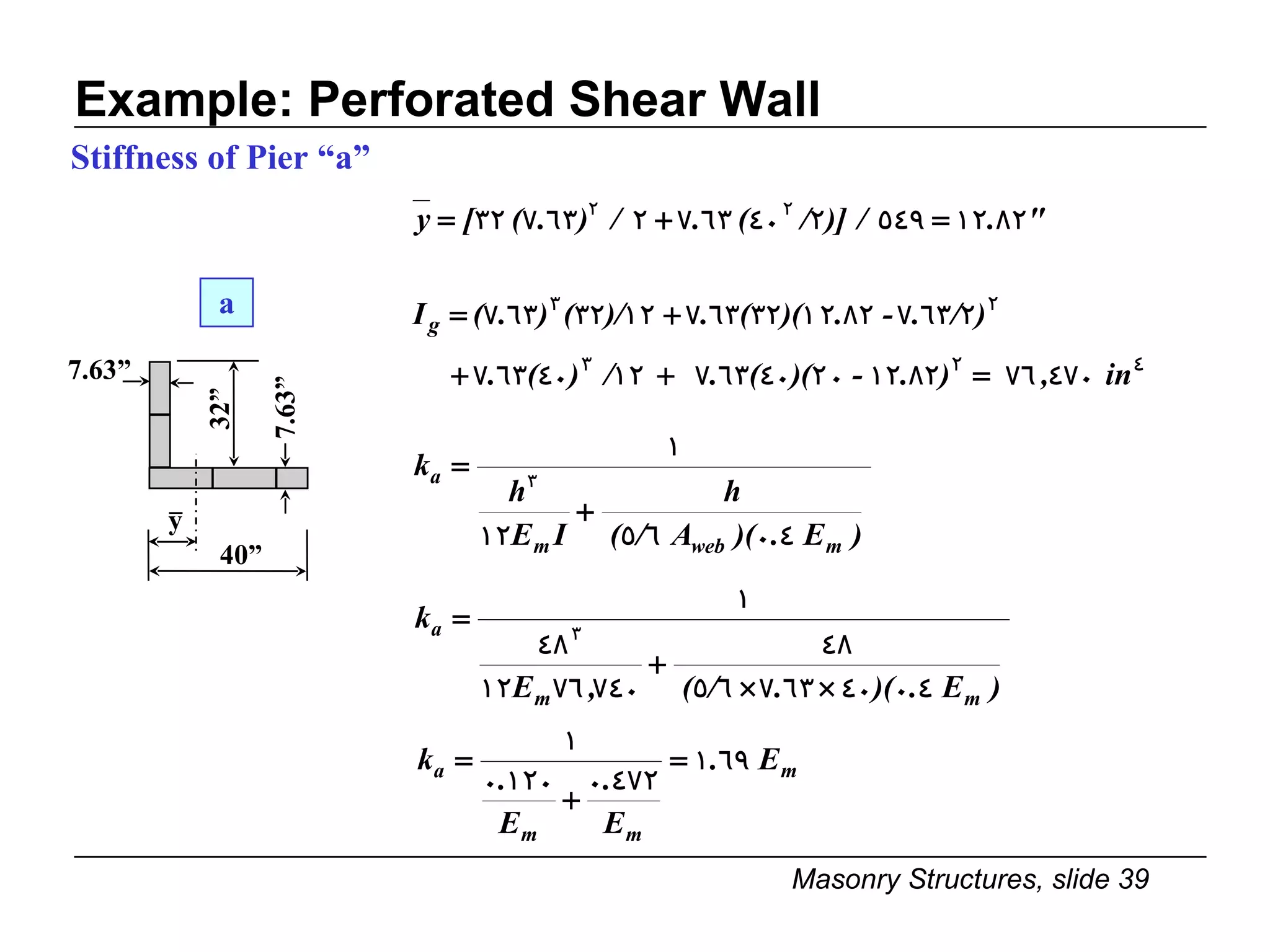
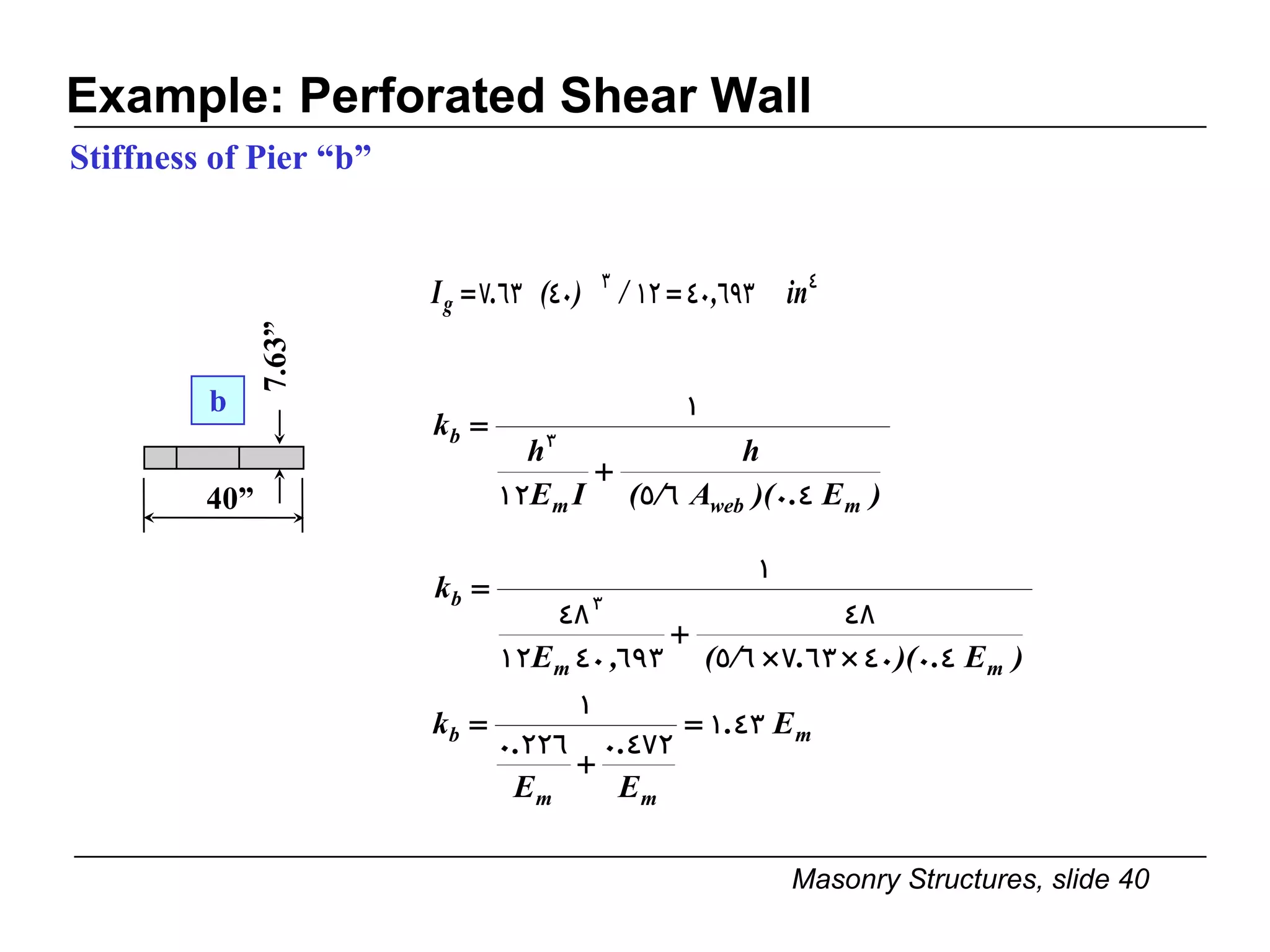
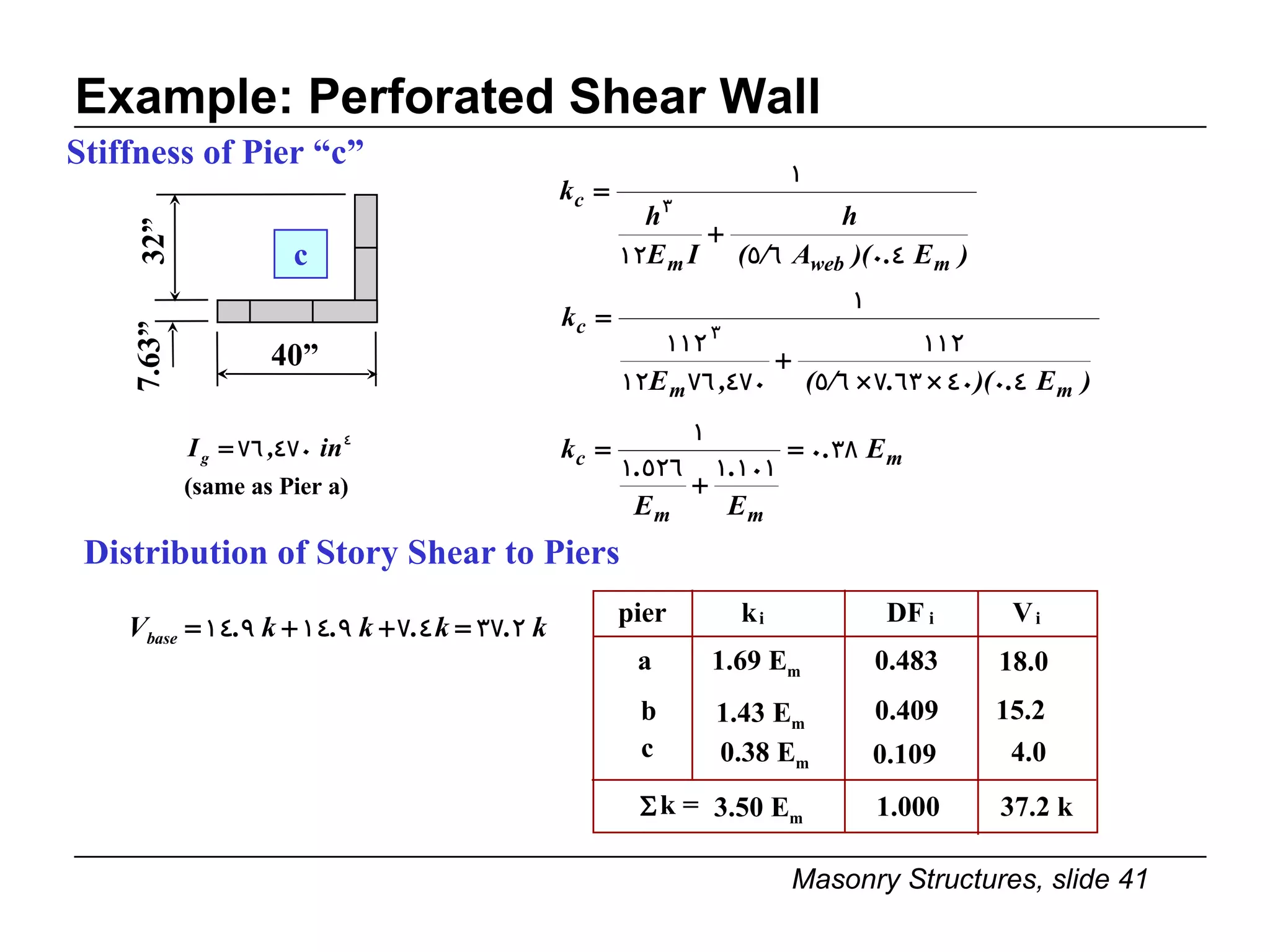
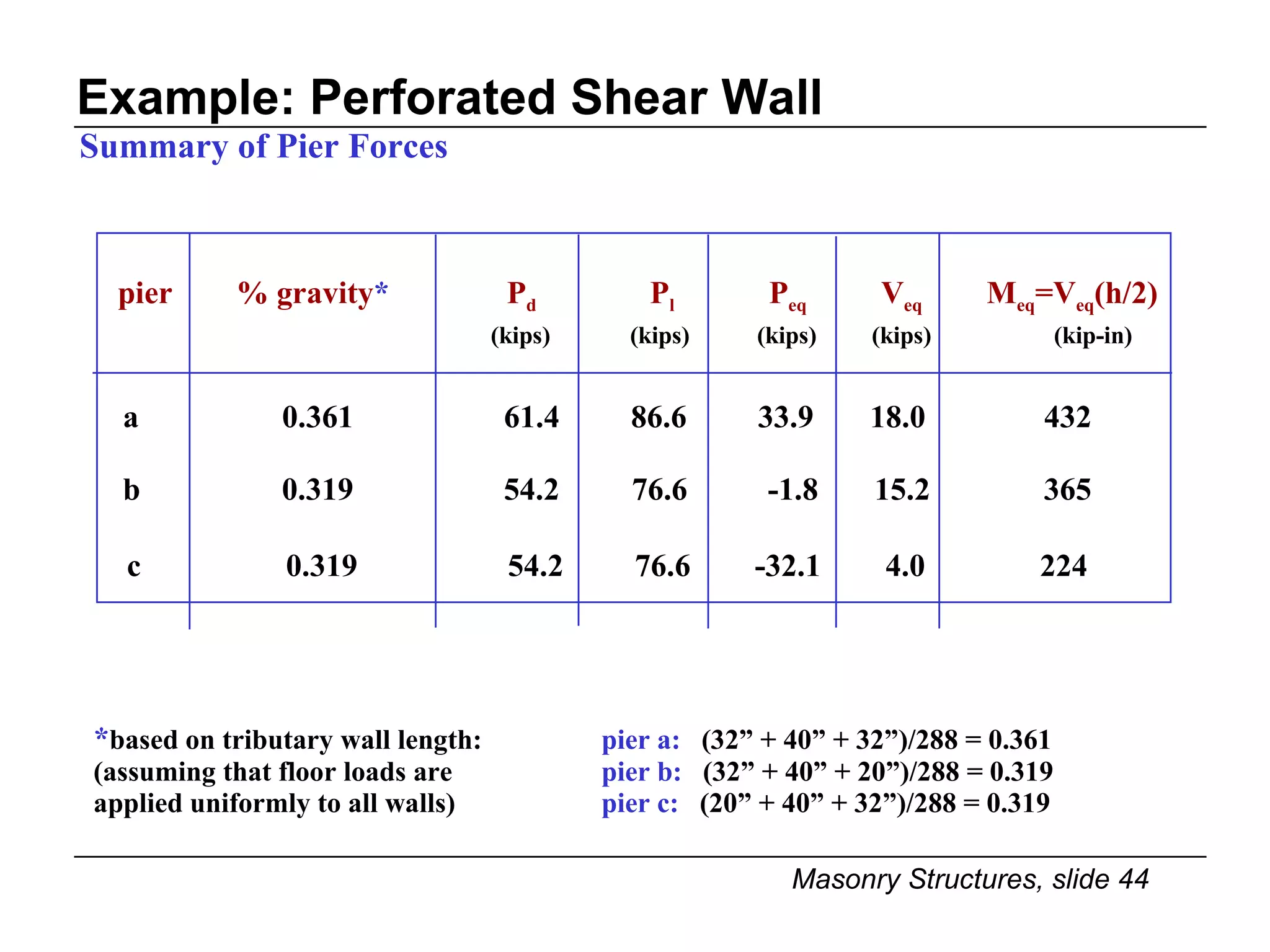
The document provides notes on masonry structures from a course at the University of Illinois. It discusses lateral strength and behavior of unreinforced masonry (URM) shear walls, including design criteria, failure modes, and examples. Key points include allowable stresses for flexure, shear, and axial loading; effects of perforations on stiffness and force distribution; and checking stresses in piers between openings.

1. Classnotes for ROSE School Course in: Masonry Structures Notes Prepared by: Daniel P. Abrams Willett Professor of Civil Engineering University of Illinois at Urbana-Champaign October 7, 2004 Lessons 4 and 5: Lateral Strength and Behavior of URM Shear Walls flexural strength, shear strength, stiffness, perforated shear walls

2. Existing URM Buildings

3. Damage to Parapets 1994 Northridge Earthquake, Filmore 1996 Urbana Summer

4. Damage Can Be Selective 1886 Charleston, South Carolina

5. Damage to Corners 1994 Northridge Earthquake, LA

6. Damage to In-Plane Walls 1994 Northridge Earthquake, Hollywood URM cracked pier, Hollywood

7. Damage to Out-of-Plane Walls 1886 Charleston, South Carolina 1996 Yunnan Province Earthquake, Lijiang

8. Likely Consequences St. Louis Firehouse 1999 Armenia, Colombia Earthquake

9. 2001 Bhuj Earthquake

10. Lateral Strength of URM Shear Walls

11. URM Shear Walls Ref: BIA Tech. Note 24C The Contemporary Bearing Wall - Introduction to Shear Wall Design NCMA TEK 14-7 Concrete Masonry Shear Walls P 3 P b h i H 3 H i H 1 P i P 1 flexural tension crack flexural compression cracks V b M b diagonal tension crack

12. URM Shear Walls Design Criteria (a) allowable flexural tensile stress: -f a + f b < F t F t given in UBC 2107.3.5 (Table 21 - I); F t = 0 per MSJC Sec. 2.2.3.2 pg. cc-35 of MSJC Commentary reads: Note, no values for allowable tensile stress are given in the Code for in-plane bending because flexural tension in walls should be carried by reinforcement for in-plane bending. where: F a = allowable axial compressive stress (UBC 2107.3.2 or MSJC 2.2.3) F b = allowable flexural compressive stress = 0.33 f´ m (UBC 2107.3.3 or MSJC 2.2.3) (b) allowable axial and flexural compressive stress: MSJC Sec. 2.2.3.1 and UBC 2107.3.4 unity formula:

13. Allowable Tensile Stresses, F t MSJC Table 2.2.3.2 and UBC Table 21-I 40 25 68* 80 50 80* 30 19 58* 60 38 60* 24 15 41* 48 30 48* 15 9 26* 30 19 29* * grouted masonry is addressed only by MSJC all units are (psi) Direction of Tension and Type of Masonry Mortar Type Portland Cement/Lime or Mortar Cement Masonry Cement/Lime M or S M or S N N tension normal to bed joints solid units hollow units fully grouted units tension parallel to bed joints solid units hollow units fully grouted units

14. URM Shear Walls Design Criteria (c) allowable shear stresses: UBC Sec. 2107.3.7 shear stress, unreinforced masonry: clay units: F v = 0.3 (f’ m ) 1/2 < 80 psi (7-44) concrete units: with M or S mortar F v = 34 psi with N mortar F v = 23 psi allowable shear stress may be increased by 0.2 f md where f md is compressive stress due to dead load Per UBC Sec. 2107.3.12 shear stress is average shear stress,

15. URM Shear Walls Design Criteria (c) allowable shear stresses: MSJC Sec. 2.2.5.2: shear stress, unreinforced masonry: F v shall not exceed the lesser of: (a) 1.5 (f’ m ) 1/2 (b) 120 psi (c) v + 0.45 N v /A n where v = 37 psi for running bond, w/o solid grout 37 psi for stack bond and solid grout 60 psi for running bond and solid grout (d) 15 psi for masonry in other than running bond Note: Per MSJC Sec. 2.2.5.1, shear stress is maximum stress,

16. URM Shear Walls Design Criteria (c) allowable shear stresses: f vmax f vavg for rectangular section

17. URM Shear Walls Possible shear cracking modes. strong mortar weak units through masonry units Associated NCMA TEK Note #66A: Design for Shear Resistance of Concrete Masonry Walls (1982) low vertical compressive stress sliding along bed joints weak mortar strong units stair step through bed and head joints

18. Example: URM Shear Walls Determine the maximum base shear per UBC and MSJC. 5000 lb. DL H H 9’- 4” 9’- 4” 6’ - 8” 8” CMU’s with face shell bedding block strength = 2800 psi Type N Portland cement lime mortar special inspection provided during construction Net section with face shell bedding: 80” 1.25”

19. Example Forces and Stresses: Maximum base shear capacity per UBC shear stress flexural tensile stress

20. flexural compressive stress Example Maximum base shear capacity per UBC Maximum base shear capacity per MSJC In lieu of prism tests, a lower bound compressive strength of 1861 psi will be used based on the 2800 psi unit strength and Type N mortar per MSJC Spec. Table 2. shear stress

21. Example Maximum base shear capacity per MSJC flexural tensile stress flexural compressive stress shear stress tension compression axial and flexural stress UBC MSJC 7890 11,857 1194 V b max Summary: 10,629 11,934 794

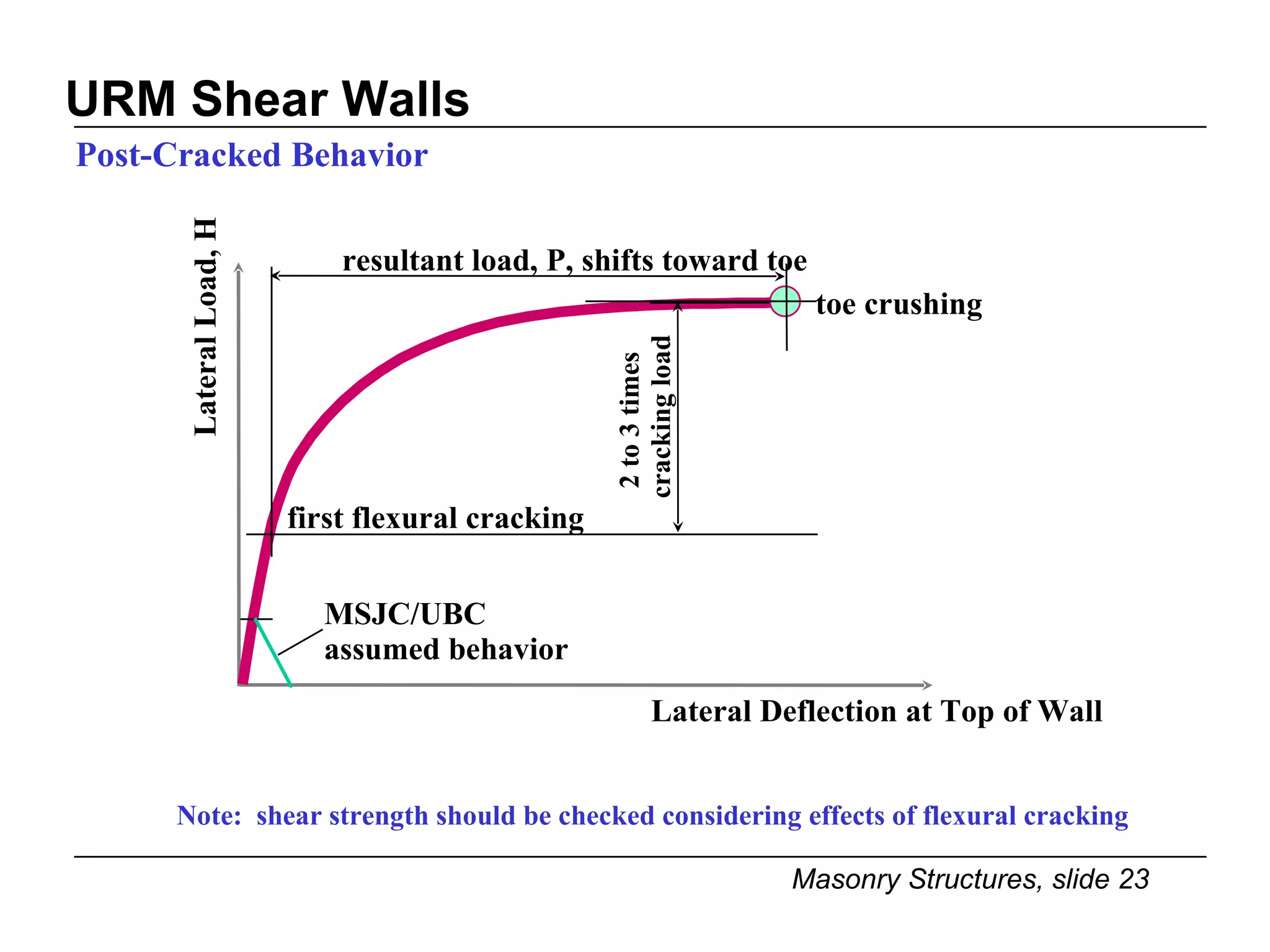
22. URM Shear Walls Post-Cracked Behavior h toe f m < F a e L/2 width = b heel H P [1] [2] [3]

23. URM Shear Walls Note: shear strength should be checked considering effects of flexural cracking Post-Cracked Behavior Lateral Load, H Lateral Deflection at Top of Wall first flexural cracking resultant load, P, shifts toward toe toe crushing 2 to 3 times cracking load MSJC/UBC assumed behavior

24. Perforated URM Shear Walls

25. Lateral Stiffness of Shear Walls Cantilevered shear wall H L h

26. Lateral Stiffness of Shear Walls Pier between openings H H h L

27. Lateral Stiffness of Shear Walls 0.2 0 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 1.6 1.4 1.2 1.0 0.8 0.6 0.4 0.2 cantilever fixed pier

28. References Associated NCMA TEK Note: 61A Concrete Masonry Load Bearing Walls - Lateral Load Distribution (1981) Associated BIA Technical Note: 24C The Contemporary Bearing Wall - Introduction to Shear Wall Design 24D The Contemporary Bearing Wall - Example of Shear Wall Design 24I Earthquake Analysis of Engineered Brick Masonry Structures

29. Example: Lateral-Force Distribution Determine the distribution of the lateral force, H, to walls A, B and C.  k i = 0.2776 bE m *based on cantilever action type of masonry and wall thickness is the same for each wall A 10’ 1.50 0.0556 bE m 0.20 10’-0” h=15’ A H 18’-0” B B 18’ 0.83 0.2077 bE m 0.75 C 6’-0” C 6’ 2.50 0.0143 bE m 0.05

30. Lateral-Force Distribution to Piers Perforated Shear Walls h 3 L 1 L 2 H V 1 V 2 L 3 L 2 V 3 h 1 h 2 equilibrium: shear force attracted to single pier: overall story stiffness:

31. Example: Lateral Force Distribution to Piers Determine the distribution of story shear, H, to each pier. A H 56” a 40” 112” 24” 64” 24” 7.63” V a Section A-A Elevation b 40” 32” V b A 8”grouted concrete block c V c

32. Example: Lateral Force Distribution to Piers piers a and c 40” 7.63” 48” 7.63” 671 7501 pier b 64” 7.63”

33. Perforated Shear Walls Axial Force due to Overturning f max f ai = ave. axial stress across pier “i” c y 1 y 2 y 3 p 1 p 2 p 3 y 1 y 2 y 3 y M [1] equilibrium of pier axial forces: [5] equilibrium of moments: [6] from similar triangles: substituting in [5]: [7] [8] [2] [3] [4]

34. Perforated Shear Walls Axial Force due to Overturning [10] solving for f max : substituting in [6]: [11] [12] [13] distribution factor for overturning moment

35. Perforated Shear Walls Design Criteria for Piers between Openings P P = P dead + P live + P lateral V V h M P M=V i h/2 flexure: reinforced piers flexure: unreinforced piers

36. Perforated Shear Walls Design Criteria for Piers between Openings P V V h M P D+L D+L P max for small lateral load M=V i h/2 0.75(D+L+W/E) D+L+W/E P max and M max for large lateral 0.9D-0.75E 0.9D+E P min for smallest moment capacity D+W shear: unreinforced piers shear: reinforced piers UBC MSJC Sec. 2.1.1 Effect Loading Combinations

37. Example: Perforated Shear Wall Check stress per the UBC for the structure shown below. Design pier reinforcement if necessary. Gravity Loads Level Dead Live 3 50 kip 80 kip Special inspection is provided f’ m = 2500 psi fully grouted but unreinforced Grade 60 reinforcement Type N mortar with Portland Cement 2 60 kip 80 kip 1 60 kip 80 kip total 170 kip 240 kip Earthquake Loads 14.9 kip 7.4 kip 10’-0” 10’-0” 9’-8” 14.9 kip 14.9 kip 18’-8”

38. Example: Perforated Shear Wall 18’-8” Pier Dimensions 9’-4” 8” grouted concrete block 3’-4” 40” 32” 3’-4” 5’-4” 3’-4” 3’-4” 3’-4” 2’-8” 4’-0” 2’-8” 7.63” a b c

39. Example: Perforated Shear Wall Stiffness of Pier “a” 7.63” 32” 7.63” 40” y a

40. Example: Perforated Shear Wall Stiffness of Pier “b” b 7.63” 40”

41. Example: Perforated Shear Wall Stiffness of Pier “c” c 32” 7.63” 40” (same as Pier a) b 1.43 E m 0.409 15.2 c 0.38 E m 0.109 4.0  k = 3.50 E m 1.000 37.2 k pier k i DF i V i a 1.69 E m 0.483 18.0 Distribution of Story Shear to Piers

42. Example: Perforated Shear Wall 7.63” 40.0” 12.82” Distribute Overturning Moments to Piers pier A i y i A i y i a 549 12.8” 7038 a  A i =1403  A i y i =160,807 124.0” b b 305 124.0” 37,820 c 211.2” c 549 211.2” 115,949

43. Example: Perforated Shear Wall total story moment = M 1 (@top of window opening, first story) = 14.9k x 23.0’ + 14.9k x 13.0’ + 7.4k x 3.0’ = 558k-ft Distribute Overturning Moments to Piers b 305 -9.38 27 41 68 -2.9 -1.8 c 549 -96.58” 5120 76 5196 -53.0 -32.1 pier (in 2 ) A i (in) (1000 in 4 ) (1000 in 4 ) (1000 in 4 ) (kips) (1000 in 3 ) I a 549 101.8” 5689 76 5765 55.9 33.9

44. Example: Perforated Shear Wall * based on tributary wall length: pier a: (32” + 40” + 32”)/288 = 0.361 (assuming that floor loads are pier b: (32” + 40” + 20”)/288 = 0.319 applied uniformly to all walls) pier c: (20” + 40” + 32”)/288 = 0.319 Summary of Pier Forces pier % gravity * P d P l P eq V eq M eq =V eq (h/2) (kips) (kips) (kips) (kips) (kip-in) a 0.361 61.4 86.6 33.9 18.0 432 b 0.319 54.2 76.6 -1.8 15.2 365 c 0.319 54.2 76.6 -32.1 4.0 224

45. Example: Perforated Shear Wall Loading Combinations * UBC 2107.1.7 for Seismic Zones 3 and 4 axial compressive force, P moment, M shear, V d case 1 case 2 case 3 pier D+L 0.75(D+L+E) 0.9D-0.75E 0.75M eq 0.75V eq x1.5 * (kips) (kips) (kips) (kip-in) (kips) (in.) a 148.0 136.4 29.8 327 20.3 36 b 130.8 99.5 47.4 274 17.1 36 c 130.8 122.2 24.7 168 4.5 36

46. Example: Perforated Shear Wall Axial and Flexural Stresses, Load Case 1 = D + L pier P D+L f a F a * f a /F a (kips) (psi) (psi) * F a = 0.25f’ m [1-(h/140r) 2 ] Note that conservative assumption is used for F a calculation, r is the lowest and h is the full height. a y a 148.0 270 543 0.497 < 1.0 ok b b 130.8 430 543 0.792< 1.0 ok y c c 130.8 239 543 0.440< 1.0 ok

47. Example: Perforated Shear Wall Axial and Flexural Stresses, Load Case 2: 0.75 (D + L + E) * minimum S g is taken to give maximum f b for either direction of building sway ** F b = 0.33f’ m = 833 psi pier 0.75(P D+L+EQ ) f a =P/A F a f a /F a 0.75M e S g f b f b /F b ** f a /F a +f b /F b (kips) (psi) (psi) (kip-in) (in 3 ) (psi) a y a 136.4 249 543 0.459 327 2813 * 116 0.139 0.598 < 1.0 ok b b 99.5 326 543 0.600 274 2035 135 0.162 0.762 < 1.0 ok y c c 122.2 223 543 0.411 168 2813 * 60 0.072 0.483 < 1.0 ok

48. Example: Perforated Shear Wall minimum axial compression: check tensile stress with F t = 30 UBC Sec 2107.3.5 Axial and Flexural Stresses, Load Case 3: 0.9D - 0.75P eq * minimum S g is taken to give maximum f b for either direction of building sway ** tensile stresses pier (0.9P D -0.75P EQ ) f a =P/A 0.75M eq S g f b - f a +f b (kips) (psi) (kip-in) (in 3 ) (psi) (psi) ** a y a 29.8 54 327 2813 * 116 62 > 30 psi provide reinf. b b 47.4 155 274 2035 135 -20 < 30 psi ok y c c 24.7 45 168 2813 * 60 15 < 30 psi ok

49. Example: Perforated Shear Wall Pier Shear Stress, Load Case 4 : 0.75E * from Case 3 0.9P d -0.75P eq ** UBC 2107.3.7 pier V=0.75V eq x 1.5 f v = V/A web f ao = P/A * F v = 23 + 0.2f ao ** (kips) (psi) (psi) (psi) a y a 20.3 67 54 34 < 67 provide shear reinf. b b 17.1 56 155 54 < 56 provide shear reinf. y c c 4.5 15 45 32 > 15 ok

50. Case Study: Large-Scale Test

51. Georgia Tech Large-Scale Test photo from Roberto Leon 24’

52. Final Crack Pattern slide from Roberto Leon Load Direction

53. Final Crack Pattern Load Direction slide from Roberto Leon

54. Results- Global Behavior Wall 1 Force-Displacement Response

55. Overturning Effect (Vertical Stress) Base strains recorded during loading in the push and pull direction slide from Roberto Leon

56. USA CERL Shaking Table Tests photos from S. Sweeney 12’

57. Damage on North Wall Permanent offsets of 0.25” – 0.35” due to rocking of pier. Final Cracking Pattern slide from S. Sweeney

58. Peak Force vs. Deflection slide from S. Sweeney

59. End of Lessons 4 & 5