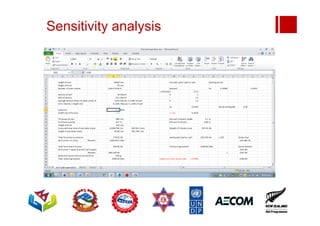
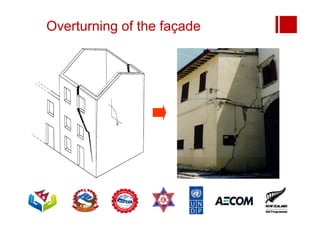
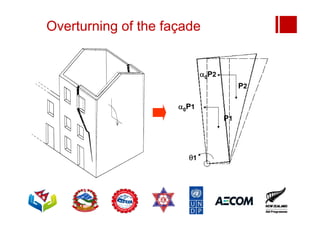
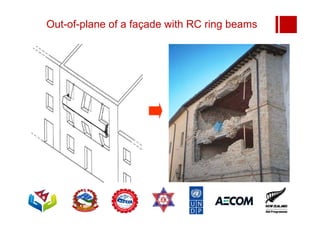
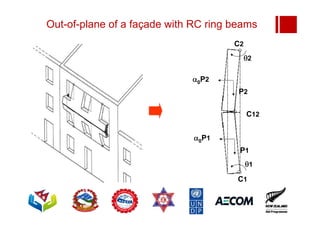
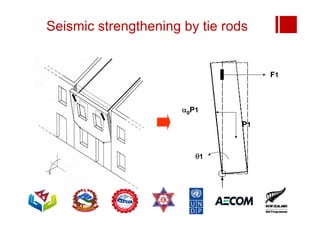
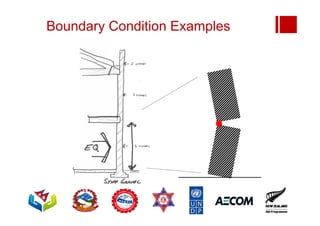
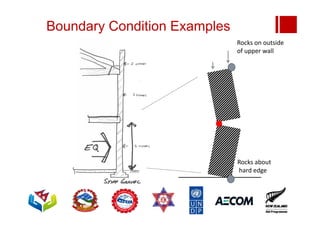
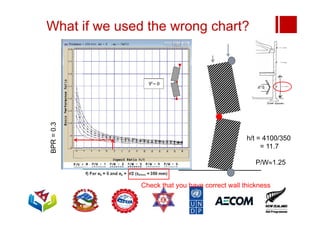
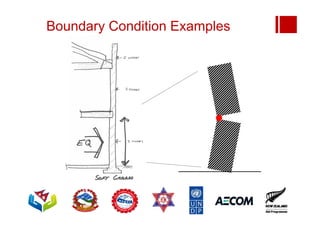
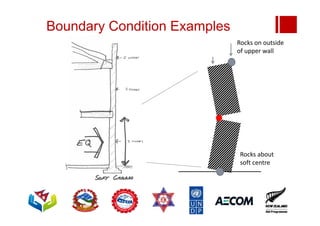
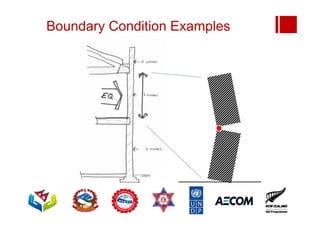
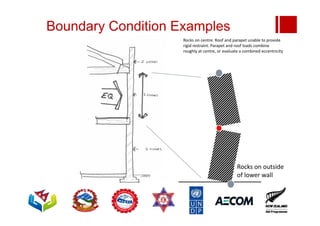
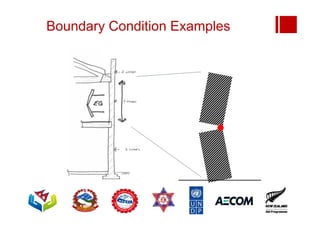
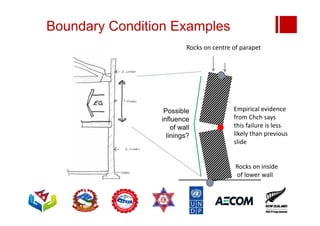
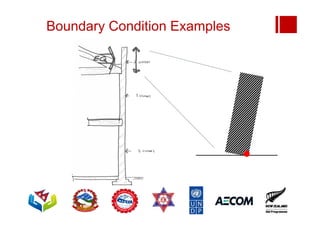
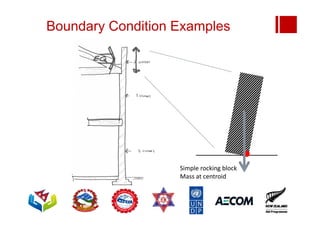
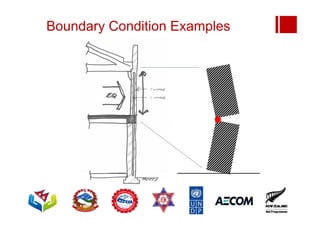
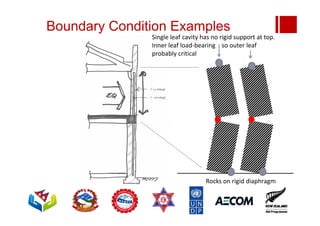
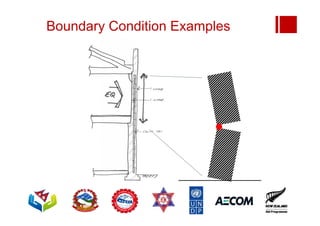
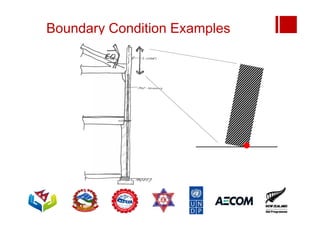
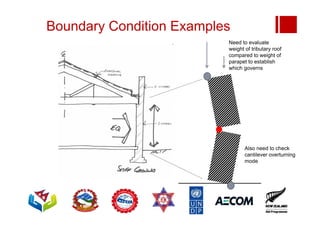
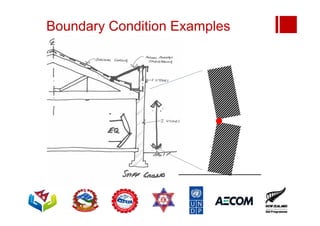
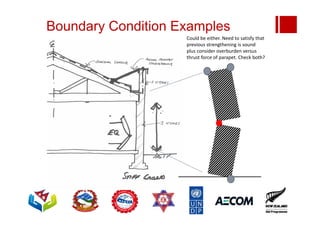
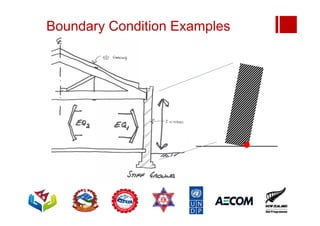
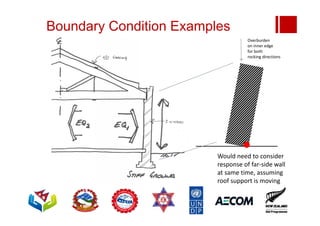
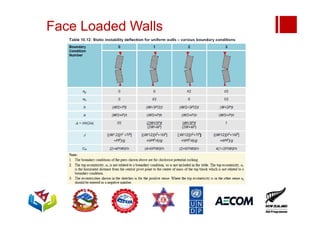
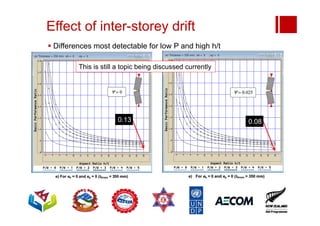
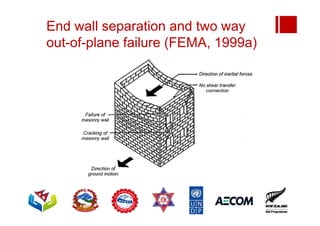
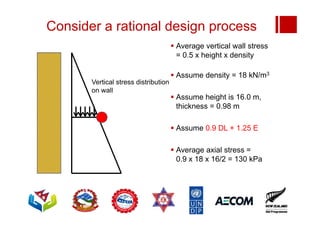
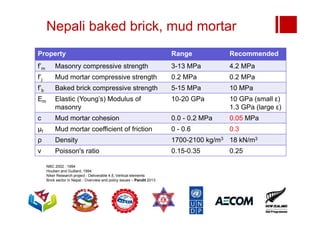
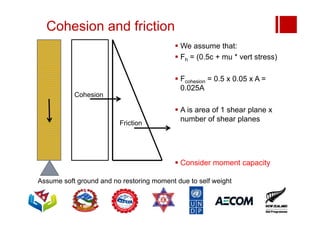
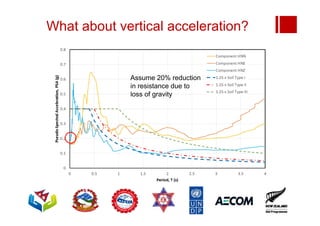
Boundary conditions and end wall separation are important factors in unreinforced masonry building assessment. Proper boundary conditions are needed to control out-of-plane failure modes. End wall separation is a common failure that can lead to two-way bending failure of the face loaded wall. A sensitivity analysis considering factors like cohesion, friction, and seismic demand shows how a wall's capacity may drop below code requirements depending on conditions. Self weight provides an important restoring force if rocking about an edge that was not considered in the analysis.

1. Module 1:
Unreinforced Masonry
Building Assessment
Session 11: Boundary conditions and end wall separation

2. Boundary Conditions
 Boundary conditions control out-of-plane failure modes
 Typically, the 1-way bending assumption is a lower bound estimate of
actual strength
 But, it may be excessively conservative
 Therefore 2-way bending needs to be considered
 But first – why so many boundary condition cases in Section 10
appendices?

3. Boundary Condition Examples

4. Boundary Condition Examples
Rocks about
hard edge
Rocks on outside
of upper wall

5. See top plot page App 31
Check that you have correct wall thickness
h/t = 4100/350
= 11.7
P/W≈1.25
h/t = 4100/350
= 11.7
BPR
=
1.05

6. What if we used the wrong chart?
Check that you have correct wall thickness
h/t = 4100/350
= 11.7
P/W≈1.25
h/t = 4100/350
= 11.7
BPR
=
0.3

7. What is the effect of the correct
vertical boundary conditions?
 The correct boundary conditions are:
 eb = +t/2 and ep = +t/2, giving BPR = 1.05 (Top of page App-31)
 The worst possible mistake gives:
 eb = 0 and ep = -t/2, giving BPR = 0.3 (Top of page App-31)
 If you used the wrong boundary conditions you could mistakenly
assume the wall is weaker than it is:
0.3/1.05 = 30% or in reverse, 1.05/0.3 = 350% stronger than it is

8. Boundary Condition Examples

9. Boundary Condition Examples
Rocks about
soft centre
Rocks on outside
of upper wall

10. Boundary Condition Examples

11. Boundary Condition Examples
Rocks on outside
of lower wall
Rocks on centre. Roof and parapet unable to provide
rigid restraint. Parapet and roof loads combine
roughly at centre, or evaluate a combined eccentricity

12. Boundary Condition Examples

13. Boundary Condition Examples
Rocks on inside
of lower wall
Rocks on centre of parapet
Empirical evidence
from Chch says
this failure is less
likely than previous
slide
Possible
influence
of wall
linings?

14. Boundary Condition Examples

15. Boundary Condition Examples
Simple rocking block
Mass at centroid

16. Boundary Condition Examples
Simple rocking block
Mass at centroid

17. Boundary Condition Examples

18. Boundary Condition Examples
Single leaf cavity has no rigid support at top.
Inner leaf load‐bearing so outer leaf
probably critical
Rocks on rigid diaphragm

19. Boundary Condition Examples

20. Boundary Condition Examples
Full length cavity with
Proper ties and mid‐height
Wall‐diaphragm anchorage (not drawn)
Should achieve composite action
Rocks on outside of lower wall

21. Boundary Condition Examples

22. Boundary Condition Examples
For PT, the PT load will dominate over
axial load. Should be reasonably
simple P*(t/2‐a/2) calc. Unlikely to
crack
e
P

23. Boundary Condition Examples

24. Boundary Condition Examples
Need to evaluate
weight of tributary roof
compared to weight of
parapet to establish
which governs
Also need to check
cantilever overturning
mode

25. Boundary Condition Examples

26. Boundary Condition Examples
Could be either. Need to satisfy that
previous strengthening is sound
plus consider overburden versus
thrust force of parapet. Check both?

27. Boundary Condition Examples

28. Boundary Condition Examples
Overburden
on inner edge
for both
rocking directions
Would need to consider
response of far‐side wall
at same time, assuming
roof support is moving

29. Boundary Condition Examples

30. Boundary Condition Examples
As drawn. Same as earlier?
Beware that could be complete
cantilever failure?

31. Beware possible cantilever action
 Note that gable ended walls have failed mid-way up building
height
 Perhaps check multiple possible failure scenarios

32. Boundary Condition Examples

33. Boundary Condition Examples
Overburden
on inner edge
for both
rocking directions

34. Boundary Condition Examples
Overburden
on inner edge
for both
rocking directions

35. Face Loaded Walls

36. Effect of inter-storey drift
 Differences most detectable for low P and high h/t
0.08
0.13
This is still a topic being discussed currently

37. FEMA, ASCE 41-06
 Procedure is popular because of its simplicity
 Sharif et al. (2007) from UBC: Using principles of rocking
mechanics; suggests that ASCE (2007) is conservative
Pass
Versus
No pass

38. End wall separation
(or Return wall separation)

39. What is wrong with our vertical one-
way bending assumption?
1. We don’t actually have diaphragm anchorages in most cases
2. We have overlooked the end walls
 Are these end walls reliable to stabilise the face loaded wall?

40. End wall separation and two way
out-of-plane failure (FEMA, 1999a)

41. Shake table testing in Potugal

42. A mix of 2 failure modes
 Response of end wall was influenced by limited tensile capacity
of side wall

43. Extensive examples of end wall separation

44. Many buildings appear to have
particularly poor brick bonding at corners

45. End wall separation

46. End wall separation
Italy
Nepal

47. Ineffective English Bond pattern
 Bricks only overlap by 25% (or is that sometimes more like
15%?)
 Very little bed joint shear friction

48. Overlap often 40 mm or less

49. Should this wall have failed?

50. Kinematics of rigid bodies
 The Italian code has a method for
‘macro-elements’ where rigid body
motion can be conceived
 The method is based on the
principles of Virtual Work
 For a rocking cantilever, this
method reduced to an equation of
moment equilibrium

51. Consider a rational design process
 English bond overlap = 240 / 4 = 60 mm
 Reduce for mortar head joint, and poor workmanship
 Say effective average overlap = 60 – 10 – 10 = 40 mm
Page 10-79

52. Consider a rational design process
 Average vertical wall stress
= 0.5 x height x density
 Assume density = 18 kN/m3
 Assume height is 16.0 m,
thickness = 0.98 m
 Assume 0.9 DL + 1.25 E
 Average axial stress =
0.9 x 18 x 16/2 = 130 kPa
Vertical stress distribution
on wall

53. Nepali baked brick, mud mortar
Property Range Recommended
f’m Masonry compressive strength 3-13 MPa 4.2 MPa
f’j Mud mortar compressive strength 0.2 MPa 0.2 MPa
f’b Baked brick compressive strength 5-15 MPa 10 MPa
Em Elastic (Young’s) Modulus of
masonry
10-20 GPa 10 GPa (small ε)
1.3 GPa (large ε)
c Mud mortar cohesion 0.0 - 0.2 MPa 0.05 MPa
μf Mud mortar coefficient of friction 0 - 0.6 0.3
ρ Density 1700-2100 kg/m3 18 kN/m3
ν Poisson's ratio 0.15-0.35 0.25
NBC 2002 : 1994
Houben and Guillard, 1994
Niker Research project - Deliverable 4.5, Vertical elements
Brick sector in Nepal - Overview and policy issues – Pandit 2013

54. Cohesion and friction
 We assume that:
 Fh = (0.5c + mu * vert stress)
 Fcohesion = 0.5 x 0.05 x A =
0.025A
 A is area of 1 shear plane x
number of shear planes
 Consider moment capacity
Cohesion
Friction
Assume soft ground and no restoring moment due to self weight

55. Dimensions
16 m

56. NBC 109 reports standard brick size
 Masonry is is a modular material
 Dimensions are scales of the basic module size

57. Moment due to cohesion
 Height = 16,000 mm
 Height of brick approx 70 mm (including joint)
 Shear plane = 0.98 m x 0.04 m = 0.039 m2 ( = 393 cm2)
 Number of shear planes = 16000 / 70 (brick height) = 229 planes
 Total cohesion force = 0.025 x 0.039 x 229 = 224 kN
 Moment due to cohesion F = 224 x (16/2) m = 1796 kNm

58. Moment due to friction
 Average axial stress = 0.9 x 18 x 16/2 = 130 kPa
 Shear plane = 0.98 m x 0.04 m = 0.039 m2 ( = 393 cm2)
 Number of shear planes = 16000 / 70 (brick height) = 229 planes
 Total friction force = (0.3 x 130) x 0.039 x 229 = 349 kN
 Moment due to friction F = 349 x (16/3) m = 1862 kNm
 Total moment capacity = 1796 + 1862 = 3657 kNm

59. What about vertical acceleration?
Assume 20% reduction
in resistance due to
loss of gravity

60. Moment due to friction
 Average axial stress = 0.9 x 18 x 6/2 = 48.6 kPa
 Shear plane = 0.98 m x 0.04 m = 0.039 m2 ( = 393 cm2)
 Number of shear planes = 16000 / 70 (brick height) = 229 planes
 Total friction force = (0.3 x 130) x 0.039 x 229 = 349 kN
 Moment due to friction F = 349 x (16/3) m = 1862 kNm
 Total moment capacity = 1796 + 1862 = 3657 kNm
 Reduced moment capacity = 80% x (1796 + 1862) = 2926 kNm

61. Determine period of cantilever
 h = 16.0 m, t = 0.98 m
 Cantilever period = 3.25 seconds

62. Consider spectral acceleration in earthquake
Spectral acceleration at Tp = 3.25 sec
approx. 0.28g

63. What would code demand be?
Z = 1
I = 1.5
P = 1.5
1.25 C(Tp) = 0.13 x 1.5 x 1.5 = 0.29
Ie the same value

64. Earthquake demand
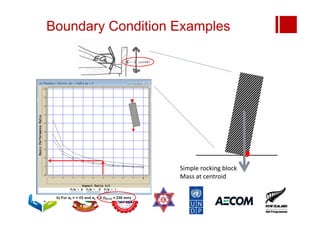
 Tributary weight for half wall:
 (0.9 x 18) x [(5.2 +1)/2 x 1.0 x 16]
= 787 kN
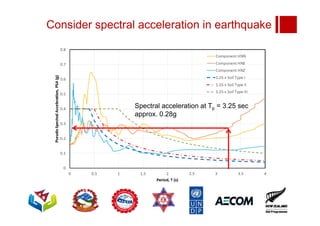
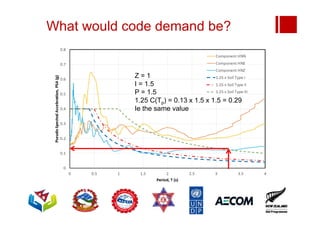
 Spectral accel = 0.28g
 Horiz demand = 0.28 x 787
= 220 kN
 Overturning moment =
220 x 2/3 x 16 = 2352 kNm

65. Sensitivity analysis

66. Capacity / demand
 Capacity = 2926 kNm
 Demand = 2352 kNm
 Ratio is that wall has 119% of required strength.
 So this explains why most did not fail
 But consider:
 20% drop in cohesion: Ratio drops to 107%
 20% drop in cohesion (poor mud mortar), 20% drop in friction, 25%
increase in shaking at site
 Ratio drops to only 76% of code

67. Capacity / demand
 Capacity = 2926 kNm
 Demand = 2352 kNm
 Ratio is that wall has 119% of required strength.
 So this explains why most did not fail
 But consider:
 20% drop in cohesion: Ratio drops to 107%
 20% drop in cohesion (poor mud mortar), 20% drop in friction, 25%
increase in shaking at site
 Ratio drops to only 76% of code
However, do recall that I also ignored
selfweight as a restoring force.
If rocking about an edge then the wall
would have a much greater restoring force

68. Capacity / demand
 Capacity = 2926 kNm
 Demand = 2352 kNm
 Ratio is that wall has 119% of required strength.
 So this explains why most did not fail
 But consider:
 20% drop in cohesion: Ratio drops to 107%
 20% drop in cohesion (poor mud mortar), 20% drop in friction, 25%
increase in shaking at site
 Ratio drops to only 76% of code
However, do recall that I also ignored
selfweight as a restoring force.
If rocking about an edge then the wall
would have a much greater restoring force
Note that the Italian method typically assumes zero tensile
strength of masonry, so self weight restoring is a factor
that is important to consider, even if then discounted

69. Exercise: assume zero tension but full rocking restoring force
16 m

70. Collapse Mechanisms
for churches
 Much work done in Europe on
this ‘macro element’ concept
 These procedures should be
directly relevant to Rana
Palaces and other similar
structures
 Italians recommend a 1.35
‘safety factor’ associated with
imperfect knowledge

71. Overturning of the façade

72. Overturning of the façade
0P1
P1
1
0P2
P2

73. Out-of-plane of a façade with RC ring beams

74. Out-of-plane of a façade with RC ring beams
0P2
P2
1
2
0P1
P1
C1
C12
C2

75. Seismic strengthening by tie rods
0P1
P1
1
F1

76. Learning lessons
 Boundary conditions significantly influence results
 If needed, you may need to revisit the site to check assumptions
 1-way bending is a lower bound value, but only applies when
diaphragm anchorages exist
 2-way bending generates demand on end walls
 Macro-element analysis is widely used in Italy for modelling
palaces and other monumental buildings
 English bond particularly vulnerable to end wall separation
 Sensitivity study is an very useful exercise