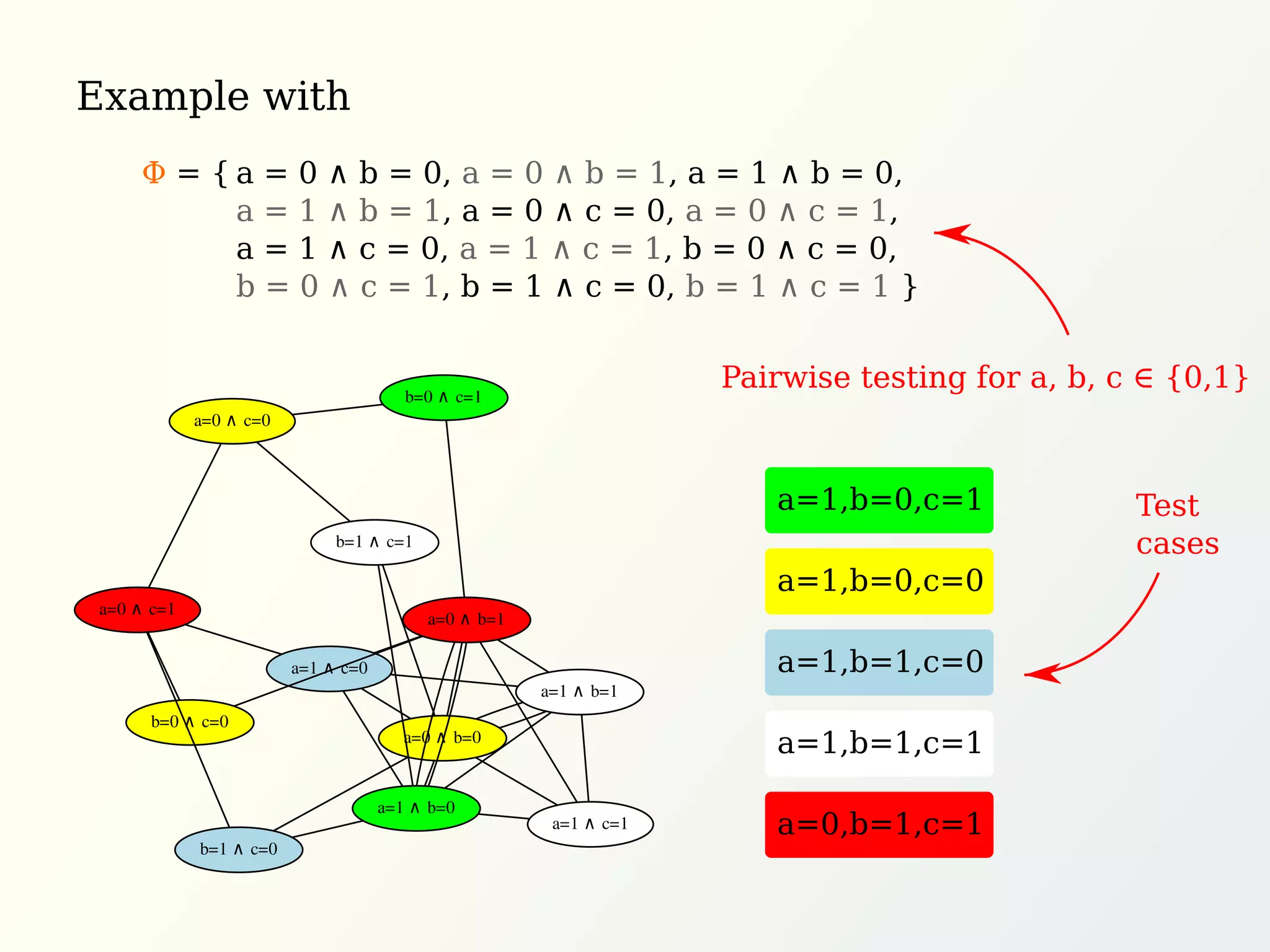
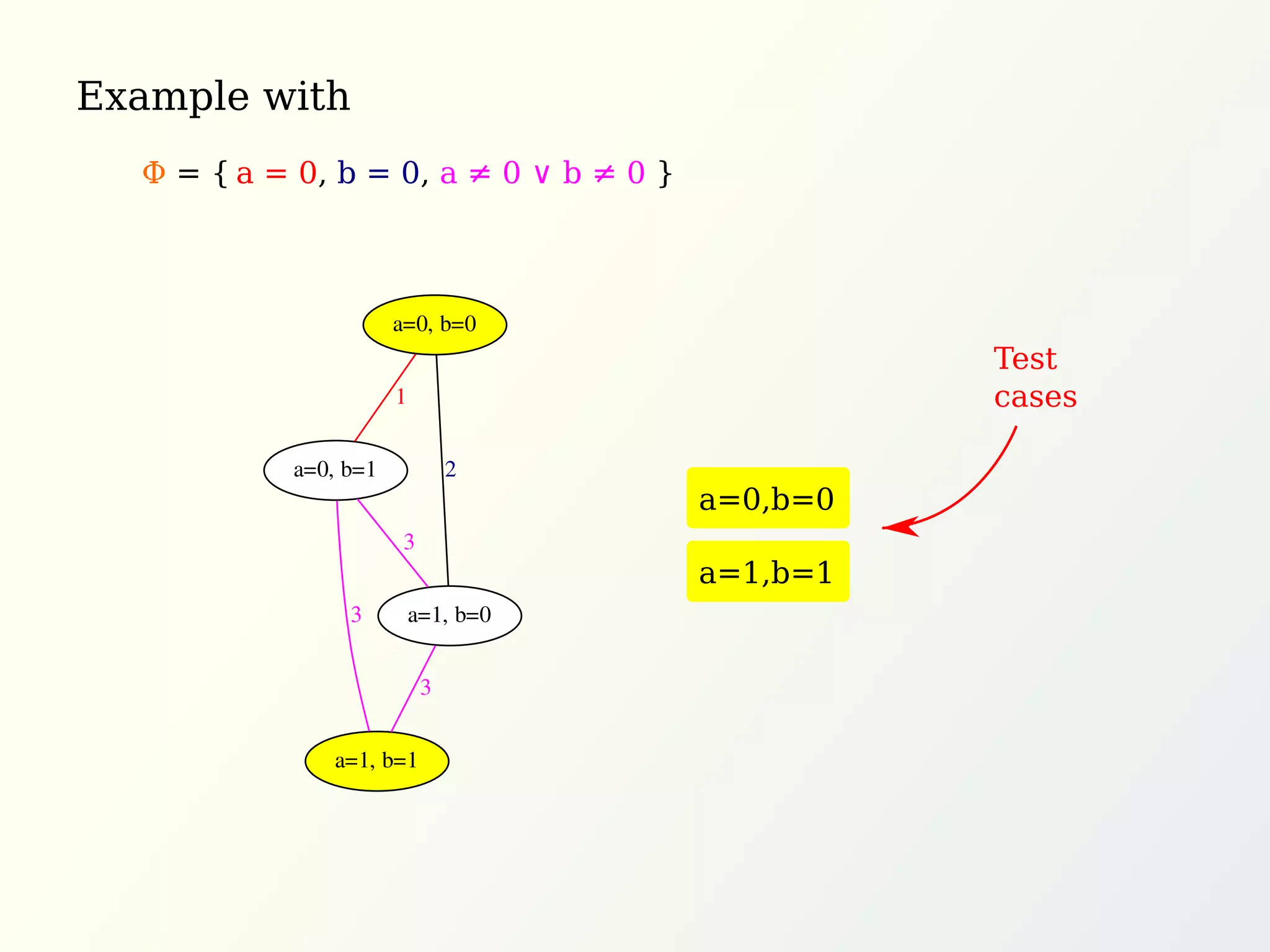
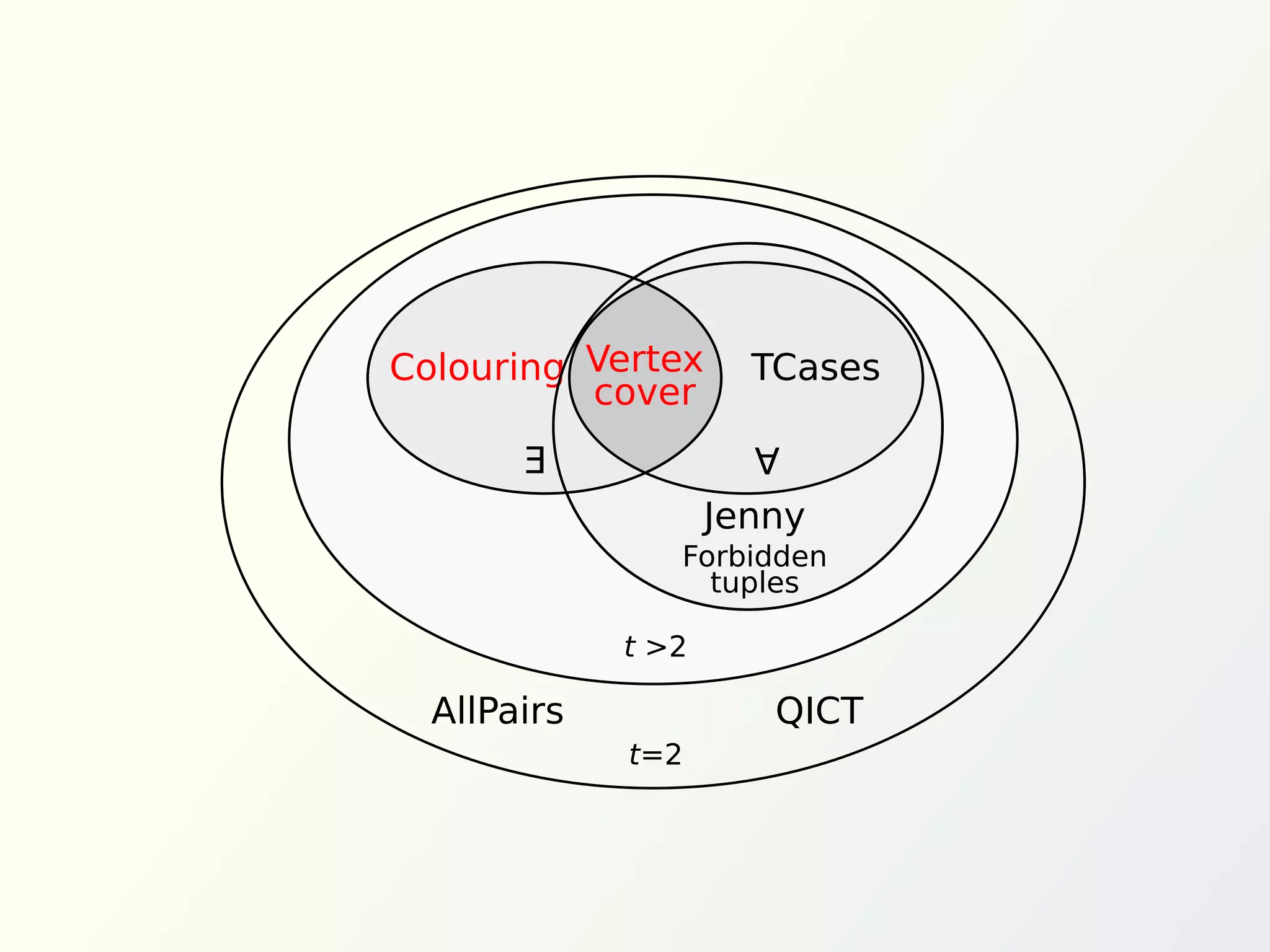
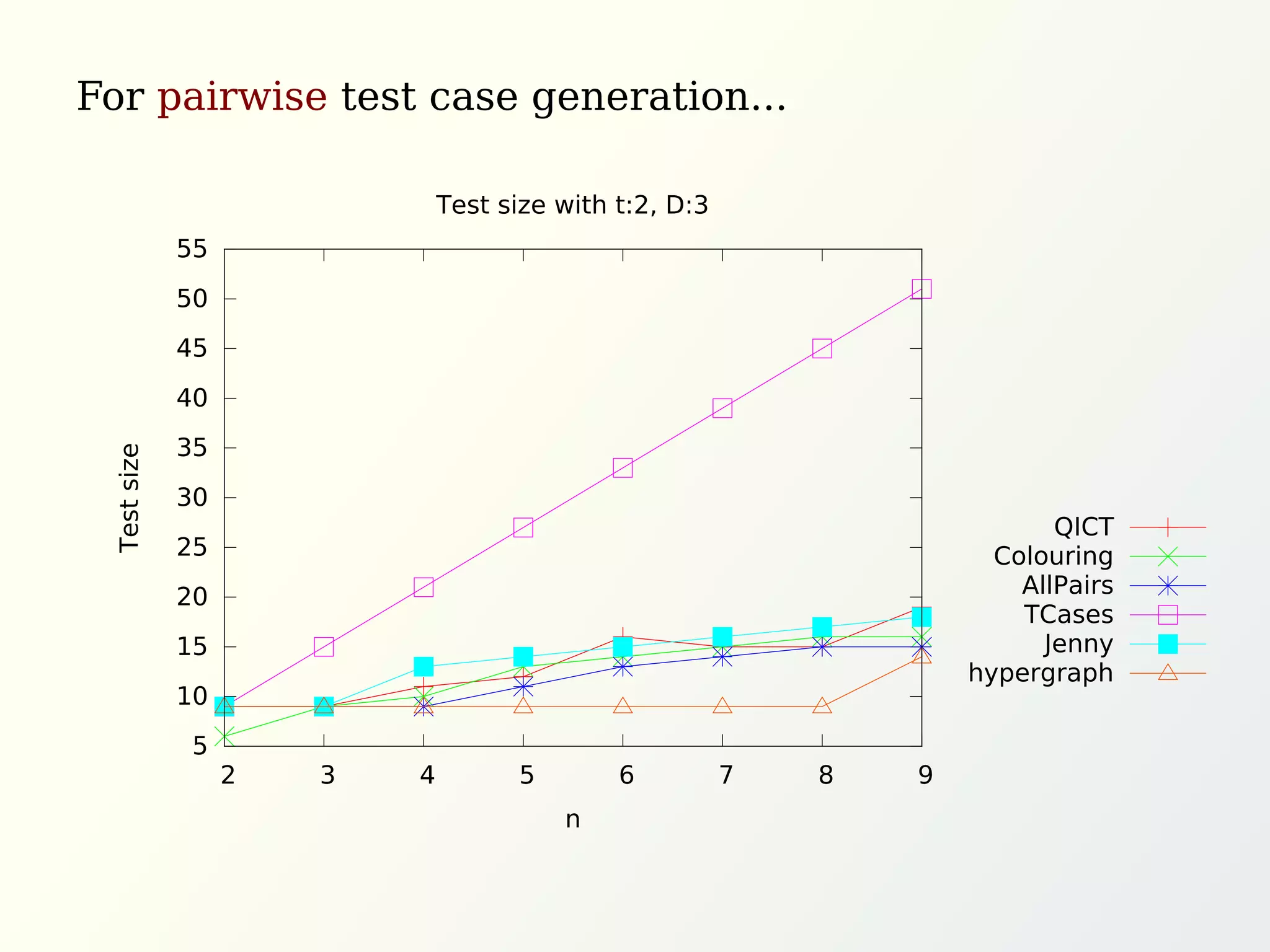
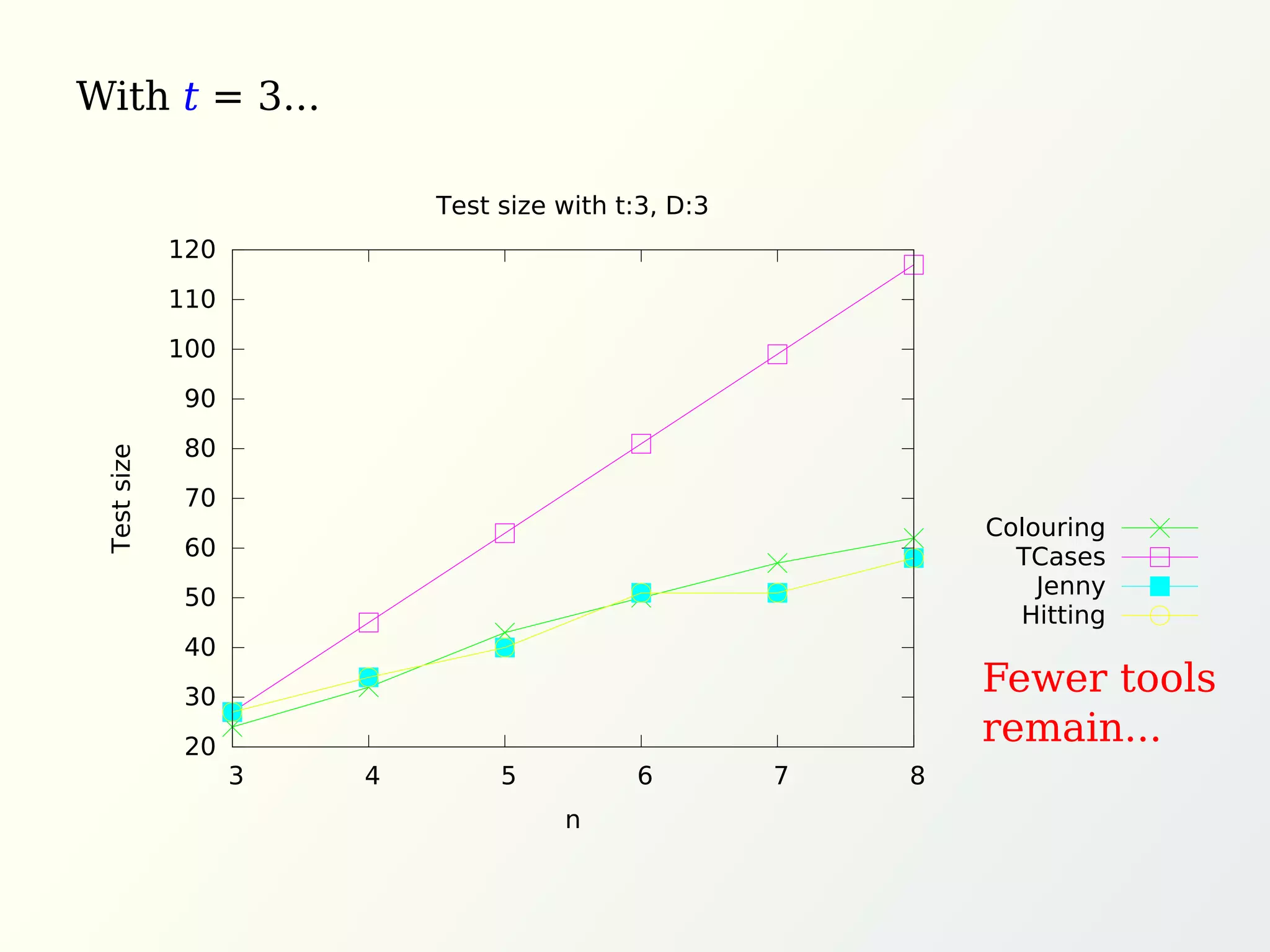
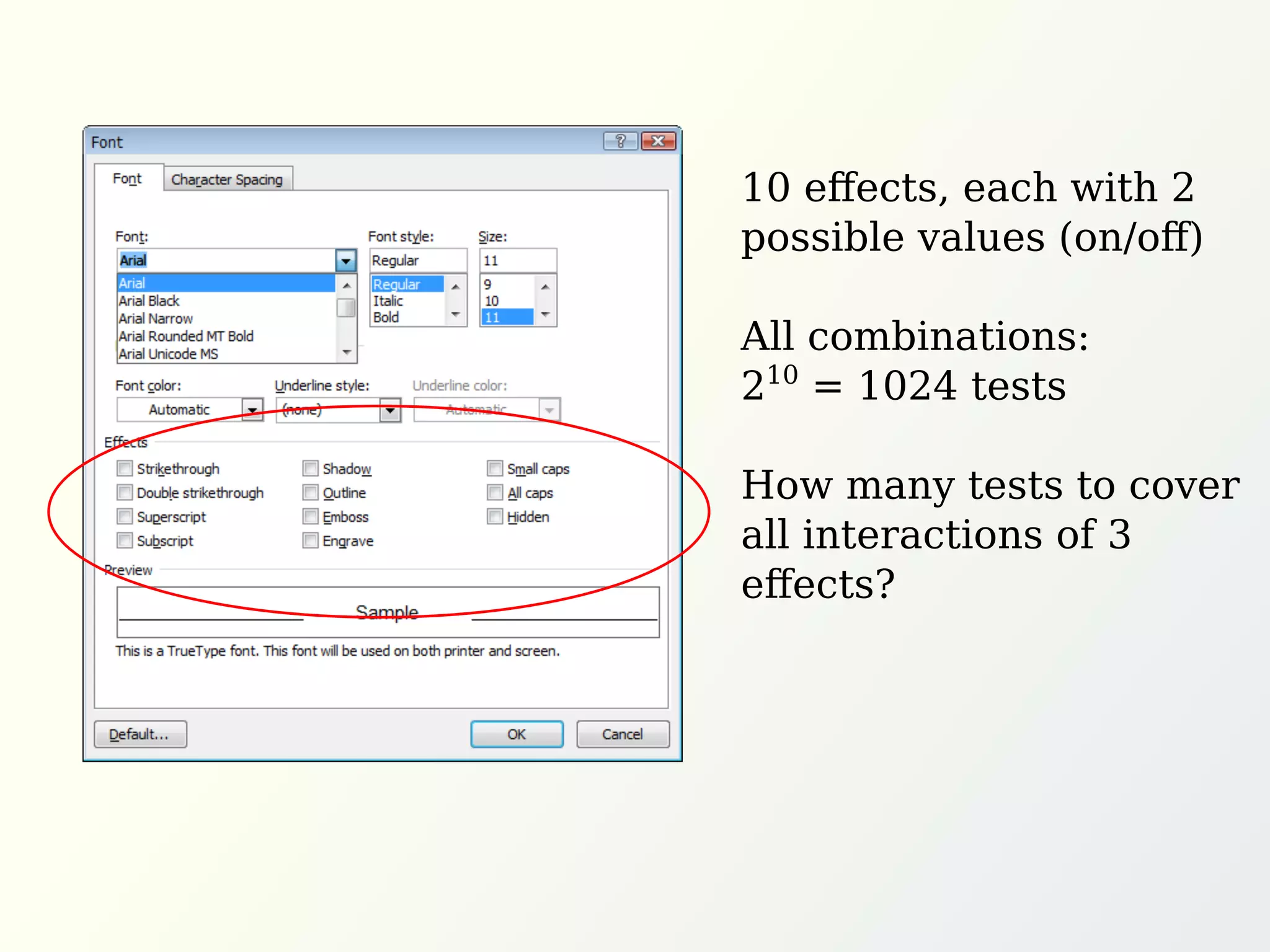
The document discusses graph methods for generating test cases incorporating universal and existential constraints to ensure comprehensive testing of software systems. It emphasizes techniques like pairwise testing and orthogonal arrays to optimize test case generation while covering all interactions between input parameters. Additionally, it introduces the concept of covering arrays to satisfy various constraints in test cases, ultimately seeking efficient solutions for validating software functionality.

1. Graph Methods for Generating
Test Cases with Universal and
Existential Constraints
Sylvain Hallé, Edmond La Chance
and Sébastien Gaboury
Université du Québec à Chicoutimi, Canada
http://www.liflab.ca
November 23rd, 2015

2. Example:
How to test the system in such a way that we cover all
possible interactions between two inputs?
can each be in position 1, 2 or 3, ,

3. Naïve method: enumerate all combinations of values
All combinations of values for any
two inputs are present
How many test cases are there?
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3
1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3

4. In fact, this table verifies all combinations of 3 inputs
exactly once... but combinations of 2 appear more than
once
Can we observe them all by doing fewer tests?
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3
1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3

5. Here's how:
Each combination of values for 2 given parameters
appears the same number of times (here, once)
We call this an orthogonal array (OA)
3 2 1 2 1 3 1 3 2
1 2 3 1 2 3 1 2 3
1 1 1 2 2 2 3 3 3
How many test
cases this time?

6. Pairwise testing
Testing strategy that identifies interactions between two
input parameters, and tests all combinations of values
for the selected pairs
Intuition: some problems occur only through an
interaction between many (e.g. 2) parameters
By varying each parameter individually, it is
unlikely to generate the pair causing the error
We can use orthogonal arrays to get the test cases
to try

7. Exemple of an interaction:
The error occurs only when altitude_adj == 0 AND
volume < 2.2
if (altitude_adj == 0) {
// do something
if (volume < 2.2) { faulty code! BOOM! }
else { good code, no problem }
} else {
// do something else
}

8. 10 effects, each with 2
possible values (on/off)
All combinations:
210
= 1024 tests
How many tests to cover
all interactions of 3
effects?

9. There are = 120 triplets of effects
For each triplet, we have to test 23
= 8 combinations of
values. We need a maximum of 960 tests.
But each test exercises three triplets; hence we need no
more than 320 test to cover everything...
0 1 1 0 1 0 1 0 1 0
...and in fact, each test covers much more than three
triplets
10
3( )
Quel est le nombre minimum de
tests?

10. Actually, only 13 tests are necessary!
Is it an orthogonal
array?
0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1
1 1 1 0 1 0 0 0 0 1
1 0 1 1 0 1 0 1 0 0
1 0 0 0 1 1 1 0 0 0
0 1 1 0 0 1 0 0 1 0
0 0 1 0 1 0 1 1 1 0
1 1 0 1 0 0 1 0 1 0
0 0 0 1 1 1 0 0 1 1
0 0 1 1 0 0 1 0 0 1
0 1 0 1 1 0 0 1 0 0
1 0 0 0 0 0 0 1 1 1
0 1 0 0 0 1 1 1 0 1

11. Covering array
An array CA(N, k, v, t) such that:
The previous array is CA(13, 10, 2, 3)
The array contains N lines
We consider k parameters
Each parameter can have v values
Each combination of values for t parameters
occurs at least once in the array
t-way test case generation

12. Back to our example:
But...
can each be in position 1, 2 or 3, ,
must always be greater than
and can never be at position
1 at the same time

13. Back to our example:
But...
can each be in position 1, 2 or 3, ,
must always be greater than
and can never be at position
1 at the same time
Universal constraints

14. Universal constraint
Constraint on the possible values for a test case
Every test case must follow the constraint to
be considered valid
We wish to find the smallest covering array
CA(N, k, v, t), for a given set of constraints
May lead to a smaller or a larger covering
array, depending on the constraints
Example: mutually exclusive parameters
(subscript/superscript)

15. Back to our example:
Also...
The test suite should
include a case where all
inputs are different
At least one test should try and
at the same position
can each be in position 1, 2 or 3, ,

16. Back to our example:
Also...
The test suite should
include a case where all
inputs are different
At least one test should try and
at the same position
can each be in position 1, 2 or 3, ,
Existential constraints

17. Existential constraint
Constraint on the possible values for a test case
At least one test case must follow the
constraint for the test suite to be considered
valid
We wish to find the smallest covering array
CA(N, k, v, t), for a given set of constraints
May lead to a smaller or a larger covering
array, depending on the constraints
Same as before

18. Why use existential constraints?
Three scenarios (at least):
See the paperb
Extending an existing test suite (add one
condition for each existing test)
Relaxed t-way (Mone combination sufficesM)
MC/DC testing

19. Let D1, D2, ..., Dk be the domains for k parameters
named p1, p2, ..., pk
Let Φ = {φ1, φ2, ..., φm} be a set of m arbitrary Boolean
expressions, whose ground terms are of the form pi = d,
or pi = pj, for d ∈ Di
Let Σ ⊆ D1 × D2 × ... × Dk be a set of value assignments
for each parameter
We call Σ a Φ-way covering if, for every φ ∈ Φ, there
exists an assignment σ ∈ Σ such that σ |= φ
Φ is the set of existential constraints
Σ is the set of test cases

20. Back to our example:
Also...
The test suite should
include a case where all
inputs are different
At least one test should try and
at the same position
can each be in position 1, 2 or 3, ,

21. Back to our example:
Also...
The test suite should
include a case where all
inputs are different
At least one test should try and
at the same position
D1 = D2 = D3 = {1,2,3}

22. Back to our example:
Also...
The test suite should
include a case where all
inputs are different
p2 = p3
D1 = D2 = D3 = {1,2,3}

23. Back to our example:
Also...
p1 ≠ p2 ∧ p2 ≠ p3 ∧ p1 ≠ p3
p2 = p3
D1 = D2 = D3 = {1,2,3}

24. Any t-way problem can be converted into a Φ-way
problem...
Let I = {S ⊆ [1,k] : |S| = t}
Let DS = Di
Define Φ as:
∩
S ∈ I {d1,...,dn} ∈ DS
∏
i ∈ S
∩ pi = di
∧i ∈ S

25. How do we find a Φ-way covering?
Two solutions based on reductions to graph
problems
Graph colouring
Hypergraph vertex covering

26. Reduction to graph colouring
Create the graph G = <V,E> such that:
Let κ : V → [1,n] be a colouring of G with n colours.
Define σκ,i as any variable assignment satisfying:
Then Σ = σκ,i is a Φ-way covering (theorem)
V = Φ
E = { (φ,φ') : φ ∧ φ' is unsatisfiable }
φ
∧φ ∈ κ-1
(i)
∩
i ∈ [1,n]

27. Informally...
Create one vertex per constraint
Link pairs of vertices that cannot be true at
the same time
Find a colouring for this graph
Create a test case for each colour (take the
conjunction of all conditions for nodes ot this
colour)

28. Example with
a = 0 ∧ b = 0, a = 0 ∧ b = 1, a = 1 ∧ b = 0,
a = 1 ∧ b = 1, a = 0 ∧ c = 0, a = 0 ∧ c = 1,
a = 1 ∧ c = 0, a = 1 ∧ c = 1, b = 0 ∧ c = 0,
b = 0 ∧ c = 1, b = 1 ∧ c = 0, b = 1 ∧ c = 1 }
Φ = {
a=0 ∧ b=0
a=1 ∧ b=0
a=1 ∧ b=1
a=1 ∧ c=0
a=1 ∧ c=1
a=0 ∧ b=1
b=1 ∧ c=0
b=1 ∧ c=1
b=0 ∧ c=0
b=0 ∧ c=1
a=0 ∧ c=0
a=0 ∧ c=1
Pairwise testing for a, b, c ∈ {0,1}
a=1,b=0,c=1
a=1,b=0,c=0
a=1,b=1,c=0
a=1,b=1,c=1
a=0,b=1,c=1
Test
cases

29. Some remarks:
The conjunction of all conditions of the same
colour must be satisfiable. Counter-example:
Classical t-way problems (and many others)
always satisfy this constraint
The minimum number of tests is the
chromatic number of G
⇒ "Guaranteed" lower bound
a=0 ∨ b=0 a=1 b=1
1.
2.
3.

30. Reduction to hypergraph vertex covering
Create the hypergraph G = <V,E> such that:
Let Σ ⊆ V be a vertex covering of G. Then Σ is a Φ-way
covering (theorem)
V = D1 × D2 × ... × Dk
E = {S ⊆ V : there exists φ ∈ Φ such that
s ∈ S iff s |= φ}
Works all the time!
Can even deal with universal
constraints (remove vertices
that violate any of them)

31. Example with
a = 0, b = 0, a ≠ 0 ∨ b ≠ 0 }Φ = {
a=0,b=0
Test
cases
a=0, b=0
a=0, b=1
1
a=1, b=0
2
3
a=1, b=1
3
3
a=1,b=1

32. a : 0, 1, 2
b : 0, 1
c : 2, 3, 4, 5
Once a != b
Once a < b
Always !(a > b) || c == 2
Both techniques implemented in a test case generation
tool
Only known tool to handle existential AND
universal constraints
Uses a simple extension of the input format
used by PICT
Domains
Existential constraints
Universal
constraints

33. t=2
AllPairs QICT
t >2
E
A
Vertex
cover
TCases
Jenny
Forbidden
tuples
Colouring

34. 5
10
15
20
25
30
35
40
45
50
55
2 3 4 5 6 7 8 9
Testsize
n
Test size with t:2, D:3
QICT
Colouring
AllPairs
TCases
Jenny
hypergraph
For pairwise test case generation...

35. With t = 3...
20
30
40
50
60
70
80
90
100
110
120
3 4 5 6 7 8
Testsize
n
Test size with t:3, D:3
Colouring
TCases
Jenny
Hitting
Fewer tools
remain...

36. With universal constraints...
With existential constraints...
Still fewer
tools...
Hypergraph
60
60
118
TCases
158
203
254
n
5
6
7
Hypergraph
65
66
110
n
5
6
7
Last one
standing!

37. Existential constraints in test case generation arise
in a variety of situations, but are not addressed by
existing tools/research
Finding an optimal test suite can be reduced to
finding the optimal solution of two well-known
graph problems
Empirically, existing heuristics for these problems
perform at least as well as a
variety of existing tools
https://bitbucket.org/
sylvainhalle/gcases
Take-home points...